带电粒子在有界匀强磁场中运动的动态问题分析

陈 燕 罗志恒

（苏州大学附属苏州十中，江苏 苏州 215006）

1 问题提出

带电粒子在有界匀强磁场中运动的动态问题是磁场教学中的重点与难点之一.因其能有效考查学生数理结合能力、读图形画图形能力、空间思维能力，此类问题成为近年高考的热点之一.以压轴题出现，其情景变化多端，难以一眼洞穿.我们可以用计算机制作动画模拟物理情景，将带电粒子运动轨迹画出，动态模拟“动态圆”变化过程，能直观形象地探究粒子的运动情况，化抽象为形象，数形结合来解决物理问题.当粒子入射点、速度方向一定，速度大小变化时，可以用“缩放圆”模型分析、解决问题.当粒子速度方向一定，速度大小变化，入射点变化时，可以用“缩放圆”“等时圆”“移动圆”等模型分析、解决问题.从实例中进行解决问题策略的研究.

2 案例分析

“新鲜出炉”的2021—2022学年度苏、锡、常、镇4市高三教学情况调研（二）中的压轴第15题，可以将物理情景转化为物理模型，用几何画板画“动态圆”模拟粒子运动情况的分析.如图1所示，某行星的赤道线，半径为R，在其赤道平面上，行星产生的磁场可以近似看成以行星中心为圆心、半径为3R的有界匀强磁场，磁感应强度为B.太阳耀斑爆发时，向该行星持续不断地辐射大量电量为q、质量为m的带正电的粒子，粒子速度方向平行，垂直于AB，速度大小介于某一范围.已知从A点射入磁场的带电粒子在磁场力的作用下恰能到达赤道线下半圆弧上的各点.不计一切阻力.

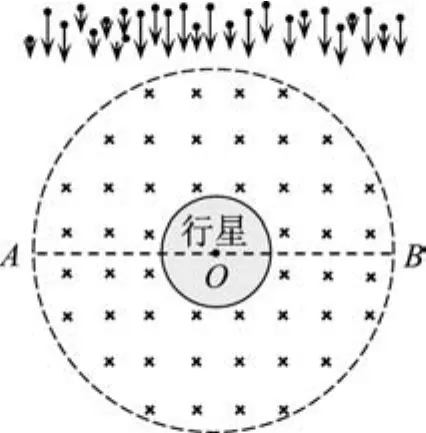
图1 粒子进入磁场运动

（1）求带电粒子的速度范围；

（2）求带电粒子从磁场边缘到行星赤道面的最短时间；

（3）带电粒子在该行星赤道上存在一段辐射盲区（不能到达的区域），求该盲区所对圆心角的正弦值.

解析：第（1）小问，从A点射入磁场的带电粒子在磁场力的作用下恰能到达赤道线下半圆弧上的各点，当粒子入射点、速度方向一定，速度大小变化时，可以用“缩放圆”模型分析、解决问题.如图2-图4逐渐增大带电粒子做匀速圆周运动的半径，也就是“缩放圆”与赤道线下半圆弧上的各点相交，粒子做匀速圆周运动的半径由R增大到2R.

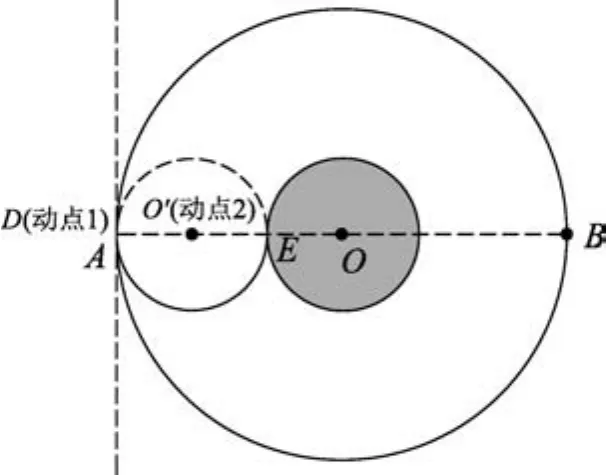
图2 粒子运动半径为R

图3 粒子运动半径R＜r＜2R

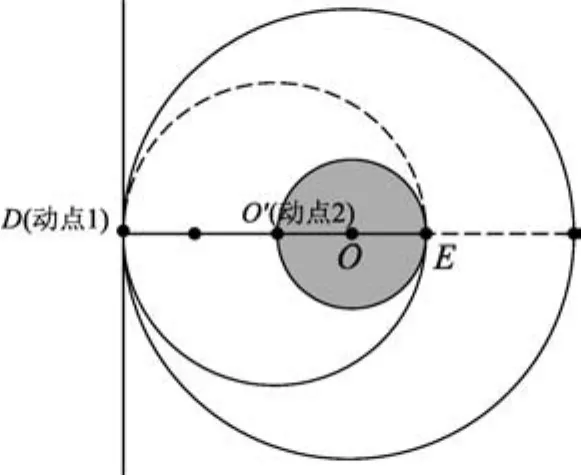
图4 粒子运动半径r=2R

第（2）小问，辐射大量电荷量为q、质量为m的带正电的粒子，在匀强磁场中运动的周期，可以用几何画板画出半径为R到2R的大小变化的“等时圆”，“动态等时圆”的动点D沿着磁场区域的外边界即半径为3R的大圆上运动，模拟速度竖直向下的带电粒子的运动轨迹.带电粒子从磁场边缘到行星赤道面的时间要短，即图5中的“等时圆”实线部分圆弧（弦长l）对应的圆心角2α要小，弦长l要短，粒子做圆周运动的半径r要大.如图6示，粒子做圆周运动在磁场区域的弦正好与磁场的半径重合，此时弦长l最短是2R，粒子做圆周运动的最大半径为2R，此时，对应的最小圆心角

图5 粒子进入磁场运动的“等时圆”

图6 半径2R弦长最短“等时圆”

第（3）小问，可以用几何画板画出半径为R到2R的大小变化的“动态圆”，“动态圆”的动点D沿着磁场区域的外边界即半径为3R的大圆上运动，模拟速度竖直向下的带电粒子的运动轨迹，可以看出从不同点竖直向下射入环形匀强磁场区域的速度不同的粒子到达赤道线圆弧上的不同点.带电粒子运动速度大小一定，即“动态圆”的半径一定，越靠右竖直向下进入磁场区域的粒子到达赤道线圆弧上的位置越靠右，如图7、8比较所示.当此半径一定的动态圆与赤道线圆弧相切时如图8所示，即此速度的带电粒子能到达赤道线圆弧上的最靠右位置.若增大粒子入射速度，即增大“动态圆”半径，则粒子能到达赤道线圆弧上的更靠右位置，如图9所示.带电粒子运动半径最大为2R，它能够打到该行星赤道的上半圆的区域最大.如图10所示，最大速度运动粒子的圆弧轨迹与赤道上半圆弧相切点，为能辐射到赤道线圆弧上的最大区域的右上边界，半径最大为2R的“动态圆”的动点D沿着磁场区域的外边界即半径为3R的大圆弧上顺时针方向运动，可得到涂色部分所对应的赤道线圆弧线部分即带电粒子能打到的区域，剩下的赤道线圆弧线部分为带电粒子辐射盲区（不能到达的区域）.

图7 速度一定、靠左入射粒子运动轨迹

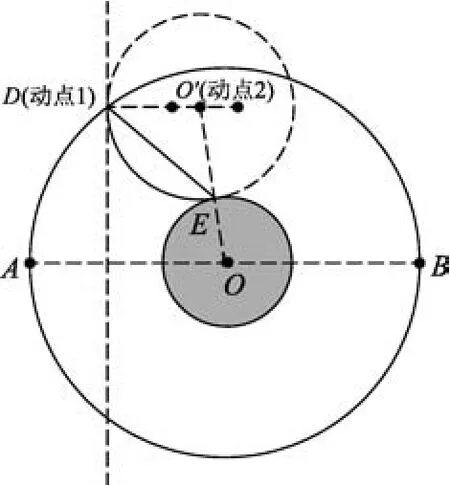
图8 速度一定、最靠右入射粒子轨迹

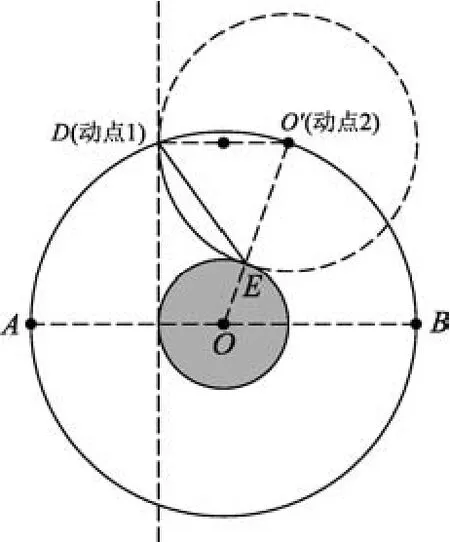
图9 速度最大、最靠右入射粒子轨迹

图10所示几何关系，△OO′C为等腰三角形，所以，.

图10 最大“动态圆”显示辐射区域

三角形底边与AB平行，所以辐射盲区圆心角

从第（1）小问解决分析中我们可以总归纳出带电粒子在有界匀强磁场中运动的动态问题“动圆”模型1.

模型1：“缩放圆”，如图11所示.

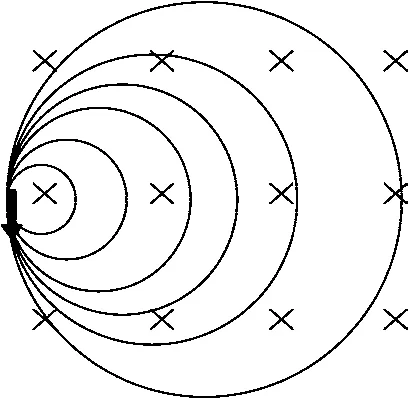
图11 “缩放圆”（半径不同的内切圆）

适用条件：带电粒子从同一点进入匀强磁场，运动速度的方向不变，大小改变即.粒子运动轨迹是半径不同的内切圆.

应用方法：以入射点为定点，圆心在垂直于初速度方向的一条直线上，将半径缩放作轨迹圆，从而探索出临界条件.

第（2）小问可以应用“缩放圆”模型分析，如图5、6所示，带电粒子从图上的同一点D以方向都是竖直向下，大小不同的速度射入有界匀强磁场中，带电粒子速度大，则其在磁场中的轨迹圆弧长度（对应弦长）在减小，如图6所示，粒子做圆周运动在磁场区域的弦正好与磁场的半径重合，最短为2R，所以圆弧长度除速度，即带电粒子从磁场边缘到行星赤道面的时间最短.

第（3）小问也可以应用“缩放圆”模型分析，如图12所示，比较从同一位置射入磁场的粒子，速度越大，即运动的轨迹圆越大，能辐射到赤道线圆弧上的点越靠右，辐射到赤道线圆弧上的区域越大，不能辐射到的区域即盲区越小.

图12 用“缩放圆”模型比较分析

从本题第（2）小问解决分析中我们可以归纳出带电粒子在匀强磁场内运动问题中“动圆”模型2.

模型2：“等时圆”.

适用条件：同一粒子以不同大小的速度射入匀强磁场，或质量和带电量相同，运动速度大小不同的粒子射入匀强磁场，即粒子做圆周运动的半径不同运动周期相等的圆.

应用方法：根据问题情景画出半径大小不等的“等时圆”，确定圆弧对应的圆心角，从而探索出临界条件.

如图13和图14两个“等时圆”，粒子做圆周运动在磁场区域的弦正好与磁场的半径重合，此时弦长l最短是2R，从两图对比中可以看出图速度大的粒子在有界匀强磁场中的运动的实线圆弧部分对应的圆心角2α小，图14中粒子做圆周运动的最大半径为2R，三角形是等边三角形，对应的最小圆心角.

图13 半径小于2R弦长最短“等时圆”

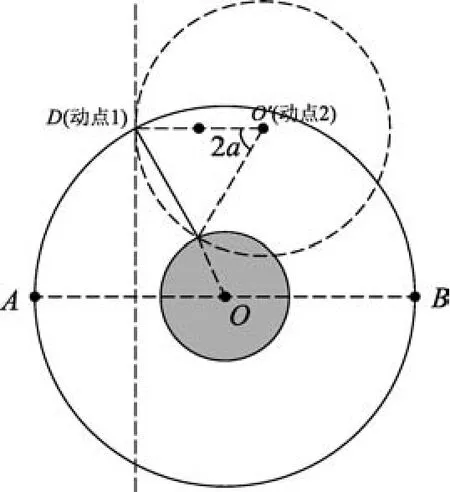
图14 半径2R弦长最短“等时圆”

从本题第（3）小问分析、解决中我们可以总归纳出带电粒子在匀强磁场内运动问题中“动圆”模型3.

模型3：“移动圆”.

适用条件：粒子的速度大小、方向均一定，入射点位置不同.

应用方法：将半径r=mv／qB的圆移动.

如图10所示，将半径为2R的圆上的点D沿着磁场区域的外边界，即半径为3R的圆弧上由A点开始沿顺时针移动，半径为2R的圆移动，可得到涂色部分所对应的赤道线圆弧线部分即粒子能打到的区域，剩下的赤道线圆弧线部分为粒子辐射盲区.

解题策略：利用“缩放圆”模型，粒子速度方向一定，大小不同，以入射点为定点，圆心在垂直于初速度方向的一条直线上，将半径缩放作轨迹圆.“等时圆”模型，质量和带电量相同，运动速度大小不同的粒子，即粒子做圆周运动的半径不同运动周期相等的圆.“移动圆”模型粒子的速度大小、方向均一定，入射点位置不同，将半径r=mv／qB的圆移动.以上3种“动态圆”模型，再结合案例中有界环形磁场区域，从而探索出临界条件.借助计算机软件辅助模拟，动态显示粒子轨迹，再应用物理规律和几何知识，数形结合解决问题.

3 反思总结

带电粒子在有界匀强磁场中运动的动态问题的解决策略如图15所示.

图15

带电粒子在有界匀强磁场中运动的动态问题，尤其是多个粒子从不同位置以相同或不同的速度、从同一位置以相同速率、不同方向或从同一位置以不同速率进入有界匀强磁场，在洛伦兹力作用下做匀速圆周运动，更需要结合几何知识确定临界条件.这是解决此类问题的关键所在，也是难点所在.往往是大家思维和方法上的难点，我们若能借助“动态圆”，将圆进行平移、缩放、旋转，形成一种“动态”的轨迹呈现，就能“化静为动”，从而消除或减少大家在解题过程中的思维、方法障碍，化繁琐为简单，化抽象为形象，问题迎刃而解.