动态过程中容器底部液体压强的分析

黄 亮

（重庆市南开中学校，重庆 400030）

非柱体类容器，各高度的横截面积不为定值.容器内的液体量在增减过程中，液体深度和增减量（体积、质量）之间不是简单的线性关系.因此，在增减流量一定的情况下，容器底部受到的液体压强与时间的函数表达式往往会比较复杂，给学生理解、教师讲授造成困扰.

例题.如图1，往浴缸中匀速注水直至注满，下列表示此过程中浴缸底部受到水的压强随时间变化的曲线（图2），其中合理的是

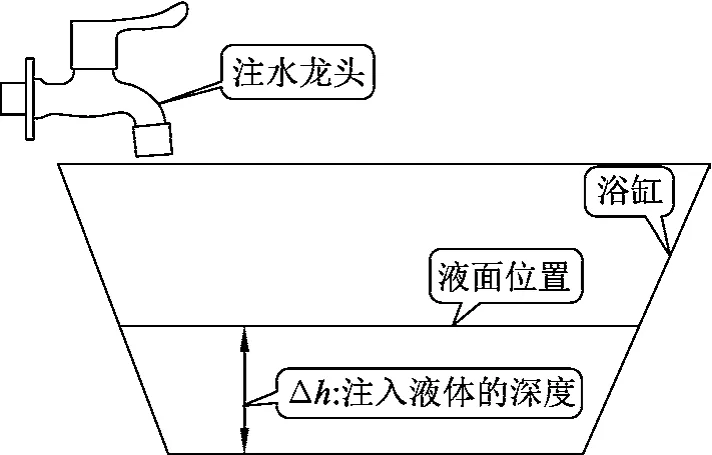
图1

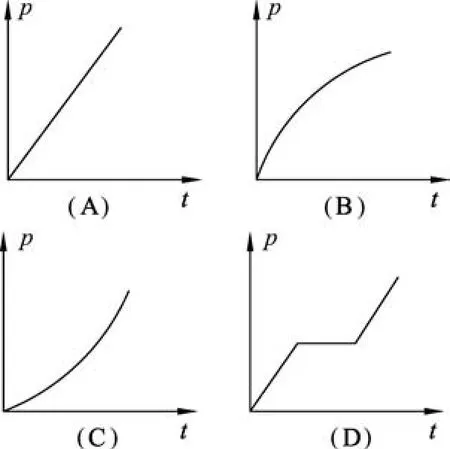
图2

该问题属于较典型的非柱体类容器底部液体压强分析.定性讲解时，强调浴缸“口大底小”，匀速注水过程中，单位时间内对应的液面上升会逐步减缓.因此，随着时间推移，浴缸底部液体压强总体增大且增速放缓，曲线“上凸”.答案为（B）.虽可顺利解题，但未经定量分析得出的结论难以反映压强的变化细节，致使学生对动态过程的认识过于感性.

以“生活实践情境”为依托对问题进行实境化归，[1]并借助数据处理软件实施工程计算，得出压强-时间（p-t）特性曲线.能直观展现压强变化特点.可帮助学生探索动态过程的内在规律.

1 模型建立

将浴缸简化为圆锥体的一部分，则已注入的水体可看作圆台（图3），水体体积可视为两个圆锥体积之差.设Q为注水流量，h0为容器底距所属圆锥体顶点距离，α为水体所属圆锥的半角，t为注水时间，且零时刻时容器内无水.

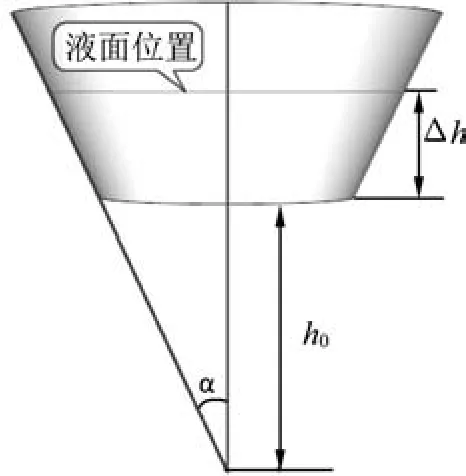
图3 浴缸示意图

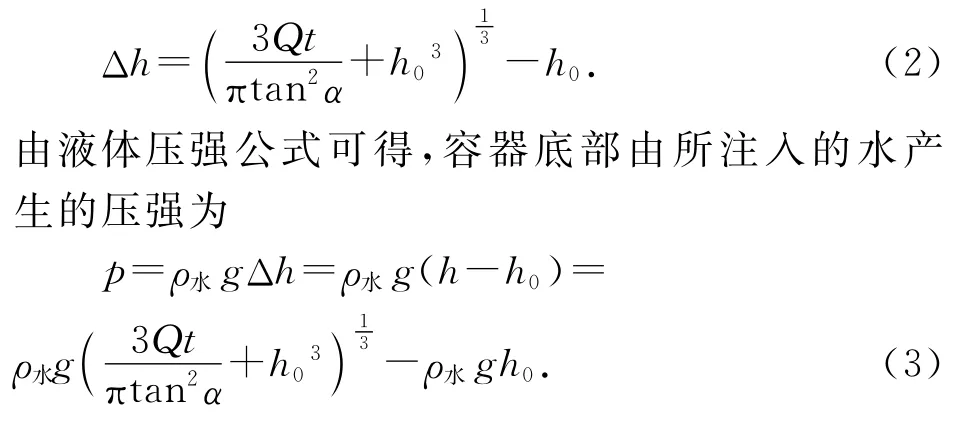
2 实境化归

参考普通圆形浴缸尺寸且注水流量取家用水龙头开启后的平均值（可参考家用12L燃气热水器工作时的出水流量）.将模型生活化、具体化.参数如下.Q=12L·min-1=0.2×10-3m3·s-1，α=55°，则有tanα≈1.428，h0=0.5m，ρ水=1.0×103kg·m-3，g=10N·kg-1.将各参数代入（3）式后，则容器底部液体压强p与注水时间t关系的解析式为

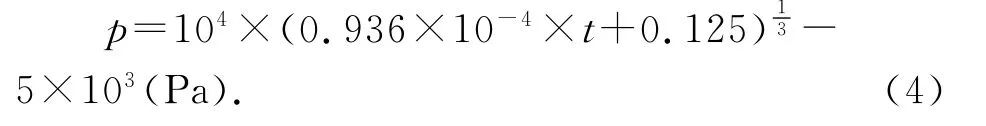
可知，当Q、h0、α均确定后，液体压强p是一个只随时间t变化的函数.

不考虑水的溢出（设容器可向上无限延伸），且忽略该过程中水流的激荡、冲击、涌动等，认为容器内水体处于理想的平衡态.忽略水的密度变化，认为容器底部所受液体压强，只与容器内水的深度有关.[3]

3 曲线绘制

在Geogebra中输入（4）式生成p-t特性曲线（图4）.

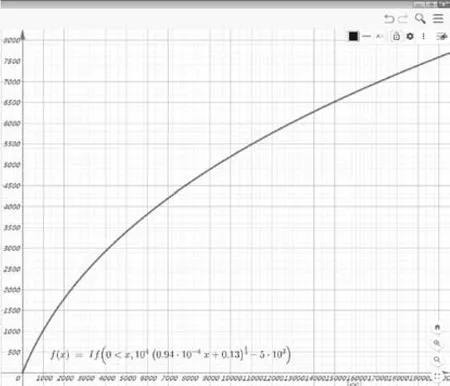
图4 p-t特性曲线

经观察得：压强随时间延续而增大，“增速”逐渐“放缓”，曲线“上凸”.该图生动直观，说服力强.可根据问题需要灵活确定起止时间，关注动态过程中的变化细节.

4 理论分析

将已注入容器中的水体旋转90°后放入直角坐标系：x轴与圆台轴线重合，其所属圆锥的顶点与坐标原点O重合（图5）.则容器内的水体可看作是直线y=（tanα）x上的某一部分线段，与其两端点到x轴的垂线段及垂足间线段组成的直角梯形平面，绕x轴旋转后形成的圆台.该旋转体体积为

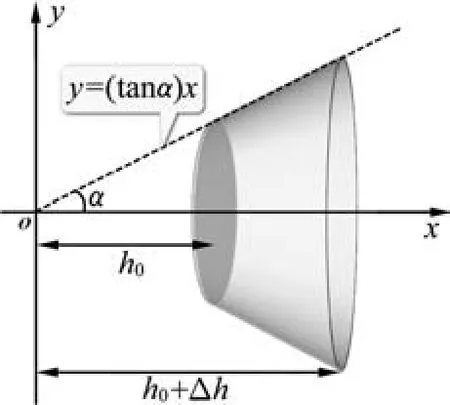
图5 圆台示意图

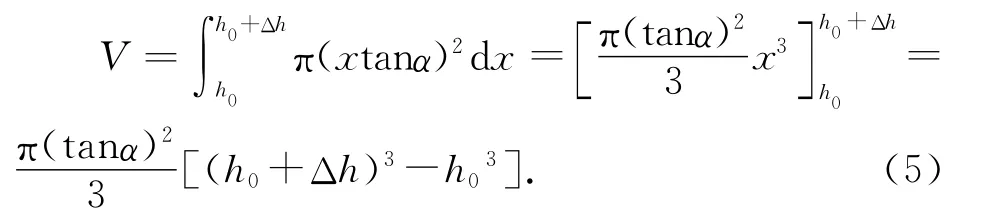
该体积等于时间t内注入的水的体积则有

由（5）、（6）两式联立可推出Δh随时间t的关系式为

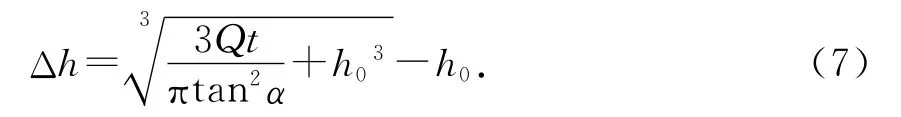
若容器不为标准圆台，而是某一函数曲线形成的旋转体，可沿用（5）式推导思路计算出新的关系 若为锥台类则可用Δh-t.的方式来论证，此处不作展开.

容器底部压强随注水时间的关系为

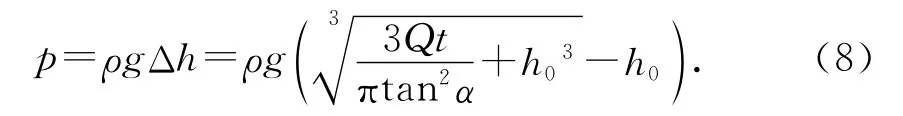
为定量讨论p的变化规律，求出p关于时间t的导数为

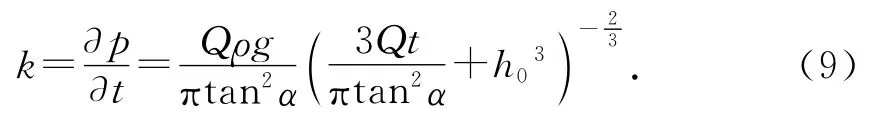
可得：在当Q、h0、α均确定后.该导数是一个只随时间t变化的函数.此函数值表征容器底受到的液体“压强变化快慢”也就是p-t特性曲线的斜率k即“压强增速”.[4]且Q、h0、α只是定义了注水快慢与容器几何形态，实际情况中均取正值，不会对该类问题的变化规律与分析方案产生本质上的影响.实境化后得出的结论具有一般性.代入Q、h0、α值后有

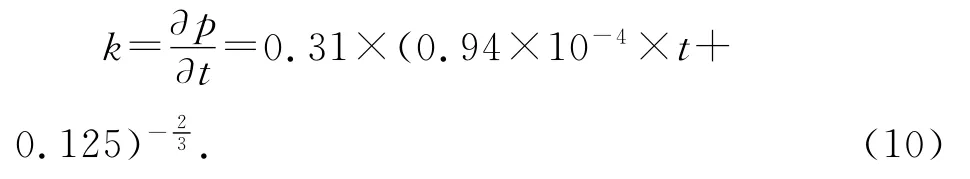
用Excel绘制（10）式图像，如图6所示.

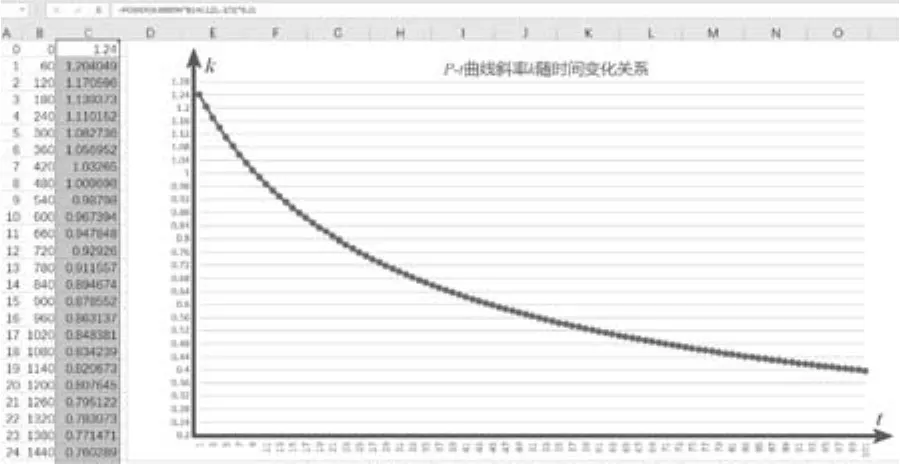
图6 斜率k随时间变化关系

不难发现：随注水时间t的推移，容器底所受液体压强的变化率始终为正且降低.意为压强始终增大，但是增速放缓.则p-t图像整体在第一象限内单调递增，斜率放缓，曲线上凸.理论分析的结果同前述结论一致.

该方案具有良好的拓展性：容器倒置类、锥台容器类、旋转体容器类、“放水”类、注放结合类等问题均可适用.特别是在学生能列出过程函数表达式，但无法进一步求解时，“描点绘图”作为较底层的数理思维，易于理解，可让定量探究有效推进.相应理论分析中的具体求解算式及参数值随问题条件变化做适当调整即可.