基于冲突分解的短波频点真实在线双拍卖算法

杨 博, 王叶群, 黄国策, 孙启禄, 王桂胜

(空军工程大学信息与导航学院, 陕西 西安 710077)

0 引 言

随着认知无线电(cognitive radio, CR)技术的发展,短波宽带频谱感知(spectrum sensing, SS)能力显著提升,在第四代自动链路建立(automatic link establishment, ALE)模式下建链速度提升明显,构建以短波认知电台为基础的短波认知通信网(high frequency cognitive communication networks, HFCCN)成为可能。短波频谱管理(high frequency spectrum management, HFSM)是指根据用户需求提供最佳可用频率,满足用户服务质量要求。短波信道具有时变特性,小区域、窄频段内大量用户同时在线会导致严重的频点干扰,如何有效提高频谱资源分配效率、提高数据链路可靠性成为亟需解决的问题。动态频谱接入(dynamic spectrum access, DSA)能够有效利用频谱空穴,设计良好的频谱接入策略,不仅能够有效降低电台间的干扰,提高频谱利用率,还可以通过频谱探测发现新的可用频点,满足实时通信需求。

当前短波频谱指配主要以静态分配为主,依据各地垂测站数据,构建电波传播模型,以降低频间干扰为优化约束条件,研究了不同算法对于系统频率指配性能的影响,该类算法对固定链路性能良好,然而在动态变化的环境中实时性差、可靠性低。HFCCN实时动态频率指配受到频点可用性影响,网络高负载情况下存在部分链路可用频点少、链路间同频干扰强等问题,需要运用DSA进行网络内不同链路的通信频点切换调整,进而提升系统通信性能。

国内外针对CR网络进行了大量研究,文献[18]对CR网络进行了概述,其中集中式网络采用在线拍卖能够实现DSA,有效提高频谱利用效率。针对频谱的在线拍卖,文献[19]提出了真实在线双拍卖(trueful online double auction, TODA)算法,在不允许抢占已分配的频谱的情况下,分析了次级用户(second-user, SU)冲突图完整时的拍卖过程。由于频点价值对各个用户存在差异,文献[20]采用了可抢占在线拍卖算法。相对于TODA算法,通过频谱可抢占策略,采用平滑临界值的定价方式,能够更加有效地分配频谱。文献[21]研究了动态频谱拍卖系统中的召回机制问题,提出了一种基于局部召回的动态双频谱拍卖机制。短波认知电台随机接入,难以确定买家、卖家数量,文献[22]设计了一个频谱双重拍卖框架,适用多个卖家和买家同时出价的情况,综合考虑了频谱的可重用性、真实性和利润最大化。短波信道受到时间、空间因素影响,同频干扰也相应发生变化,文献[23]考虑了频率分集可能导致频谱购买者之间的冲突关系不相同,并解决了干涉图变化的问题。

短波频点拍卖相较于传统频点拍卖,存在可用拍卖频点个数不确定和用户数不确定的双重不确定情形,因此既要考虑用户业务需求,又要兼顾探测时间资源分配,TODA模型能够平衡两方面收益,适用于短波频点DSA。同时,在网络高负载情况下,频点冲突严重,为减少抢占过程中网络内频点切换次数,需要分析冲突关系,构建新的频率指配模型。

本文提出一种基于冲突分解的TODA(TODA based on conflict decomposition, TODA-CD)短波频率指配方法,通过设计卖方策略和买方策略,最大化买家收益,提高频谱使用效率,同时确保算法的真实性、公平性和预算均衡。TODA-CD算法重点分析了频谱抢占对于现有网络内频谱切换次数的影响,通过对冲突频点生成频谱冲突图,分析了频点冲突状况,设置惩罚函数,完成对买家收益的建模。通过仿真发现,TODA-CD算法相比传统拍卖算法,能够提高交易成功率,有效减少切换频次,提高买家收益。

1 系统模型

1.1 HFCCN

在HFCCN中,当前获得频谱授权的用户被称为主用户(primary user, PU),也就是网络内静态分配的用户,未获得频谱授权的用户被称为SU,SU通过SS,动态接入网络。其中,SU所构成的CR网络能够利用宽带接收机实现全频段接收,使得发射端频点探测范围跳出预置频点集,实现DSA。

在SU构成的认知网络中,SU主动探测频点质量,其中为避免不同网络探测间的干扰,采用码分多址的信道接入策略,采用64阶的Wlash码进行不同网络间探测信号的区分识别。

在一个区域内,多个动态移动的短波认知电台和中心节点进行通信,完成数据的上传下达,其网络拓扑为集中式网络,如图1所示。即一个中心控制节点和多个节点相连接。在拍卖过程中,当业务请求到达时,各个节点发起链路建立请求,中心节点进行全频段扫描检测探测信号,在发现探测信号后开始建链过程,形成买方报价,提交给中心节点,中心节点根据拍卖策略,分配合适的频点给该条链路,建立链接,传输业务。业务传输结束后,拆除链接,释放频点,网络内空闲频点集增加。

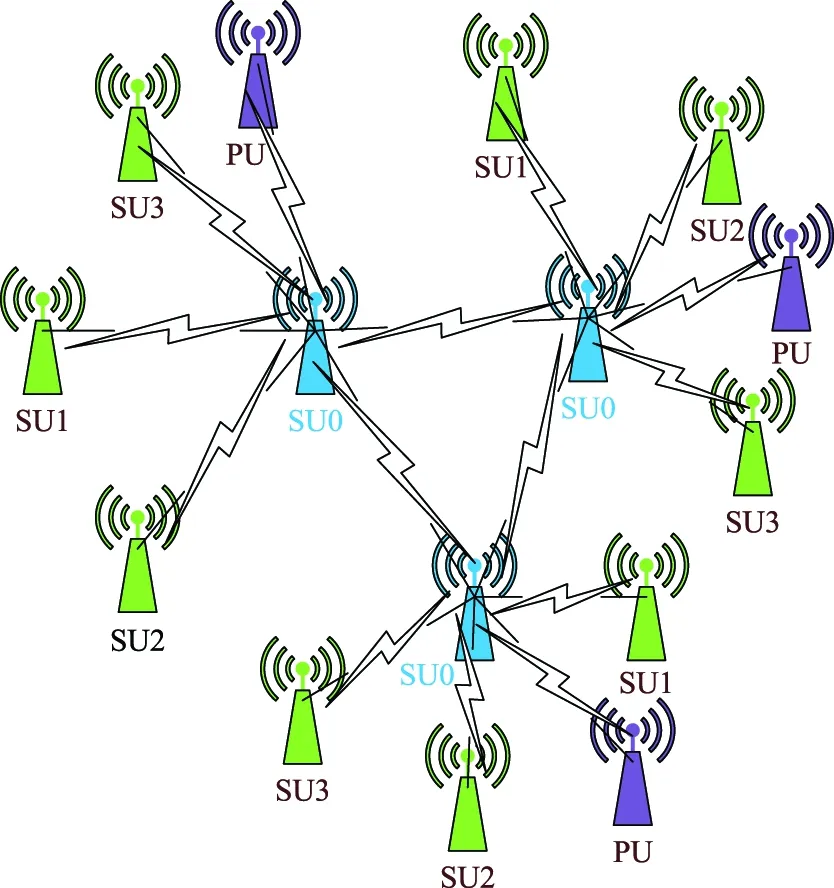
图1 集中式HFCCNFig.1 Centralized HFCCN

1.2 在线双拍卖模型

文中假设集中式HFCCN存在个CR用户{SU1,SU2,…,SU}和1个中心节点SU0。SU0与其他认知用户通过频谱探测个可用频率,构成频谱卖方=[,,…,]。在1个拍卖周期内,个用户请求建链,提出频谱申请,构成频谱买方=[,,…,]。在拍卖过程中,存在中间拍卖商,决定中标人和支付价格。拍卖采用密封第二价格拍卖,所有投标人提交密封价格,以未中标最高价格作为支付价格。假设频谱卖家提供1个空闲可用信道,频谱买方购买1个可用信道。用户到达符合参数为的泊松分布。

因此,单条链路单个周期内买方收益为

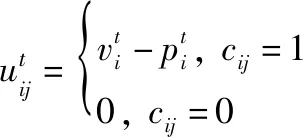
(1)

单条链路单个周期内卖方收益为

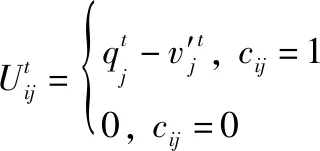
(2)

网络中个周期内买家总收益为

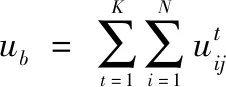
(3)

网络中个周期内卖方总收益为

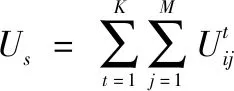
(4)

2 TODA-CD

由于短波链路质量受时间、地点等因素影响明显,不同时刻变化较大,即不同站点的不同。其中,卖家收益表征了中心节点资源的利用效率,买家收益表征各条链路收益之和,即网络内频点指配效率。因此,通过设计定价策略,兼顾卖家收益,同时,确保买家收益最大化,算法优化目标为max。

2.1 基于链路差异性的卖方模型

由于认知电台所处地理位置的不同,各条链路间差异巨大,为保证链路可靠性,需要突出关键链路的频点价值,由此构建了以链路差异化定价的卖家模型。

定义每条链路当前时刻的可用空白频点数量()=[MUF()-MLF()],其中MUF()为某时刻最高可用频率,MLF()为某时刻最低可用频率,为信道带宽。

去除干扰频点(),得到当前空白可用频点:

′()=()-()

(5)

式中:中心节点在′()进行频点质量探测。

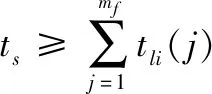
(6)

(7)

2.2 基于冲突分解的买方模型

假设业务真实估值符合参数为的均匀分布,持续时间=-,符合参数为的均匀分布。

(8)

传统在线双拍卖过程中,交易商通过Mcafee算法撮合买家与卖家,采用Kuhn-Munkres二部图最优匹配算法进行频率指配,完成交易,达到当前时刻预期收益最大值。但是,短波频点可用频点数目少,频谱拥挤程度高,在网络负载较高的情况下,使得网络内成功交易的概率急剧下降,网络频谱利用率降低。

由于买家对应的多个卖家的频点占用情况不同,最优SINR可能存在频点占用情况,在频点缺乏的情况下存在所有可用频点均被占用的情况。在链路申请频繁、占用时间较长的高负载情况下,可用频点减少,网络内拥堵,导致部分链路可用频点已被完全分配,造成通信中断。允许频点抢占能够适应高负载网络条件下的频点指配,即通过调整过往分配结果来满足新链路建链需求。在此过程中,需要平衡频点指配收益与切换次数的关系,达到相对最优,即在一定限制下通过反向切换网络内频点获得最大收益,提高频点使用率,提升系统整体收益。

(9)

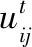
抢占的切换过程通过买家报价实现。针对频点指配结果进行广度优先搜索,进而生成频点冲突树,通过最大化频点切换带来的预期收益,改变买方的拍卖价格。切换过程为双方确认过程,额外的网络开销小。

根据买家期望收益计算,定义最优切换卖家,形成买方报价:

(10)

当频点调整时,系统通过竞价来进行补偿,进而完成频点的抢占最优切换:

(11)

竞价过程采用第二密封价格进行竞价,即采用竞价失败的最高收益价格。同时,为保证最优匹配,提高值为的报价,形成新的价格。针对新的竞价价格的期望收益为

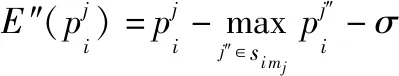
(12)

由于切换频次对系统整体性能存在一定影响,会引起系统传输的延时增大,因此对收益进行一定的罚函数处理,惩罚度为,惩罚收益为

(13)

预期收益的计算采用逐步计算法,通过广度优先算法进行预期收益的逐步递归求解。

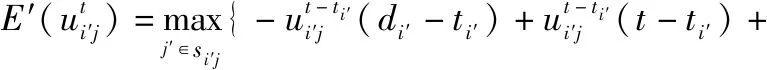
(14)

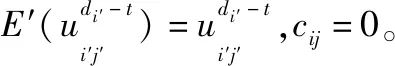
由于切换带来的每次收益的值降低,为递减函数,当搜索到空闲频点时,即取得当前切换收益的最大值,停止搜索。

由于每次切换过程带来的收益递减,搜索过程采用广度优先算法进行,通过生成当前频点切换生成树,计算最优切换方案,树的深度受空闲频点数量影响,即空闲频点越多,树的深度越小,切换次数越少,总体收益越高。

当空闲频点极少时,切换成本急剧增大,新链建链成功对总体收益影响减小,可以随机延迟一段时间重新进行链路申请,保证网络内整体收益最高。

3 算法性能分析

3.1 真实性分析

首先证明基于抢占的在线双拍卖算法是真实的,即投标人不能通过操纵其报价来提高其效用。

切换过程中,系统的竞争价格由过往系统的频点分配状况决定,由系统主导,不存在欺诈。卖方报价由系统探测时间生成,不存在欺诈性。因此,该算法是真实的。

3.2 公平性分析

从买家和卖家两个方面讨论公平性。由于频谱具有可抢占性,申请时间先后顺序对于频点的选择影响降低,保证了后接入节点的公平性。同时,通过竞争方式接入,保证了各个站点之间的公平性,可平衡各个节点业务量和频谱使用的关系。

卖方策略通过对每个频点分配相同的时间进行频点探测,保证各个站点对整个系统探测资源的公平使用,通过差异化定价,体现不同频点的探测成本。

3.3 预算平衡分析

由于系统内买方的收益始终高于卖方的成本,预算初始会保持平衡。拍卖过程中,由于买方和卖方通过竞价完成交易,使得报价趋于真实,不会出现买方整体压低报价或者卖方整体抬高报价而导致的预算失衡。

3.4 频谱利用率

通过采用可抢占的频点选择策略,提高了交易的成功率,进而提高了空闲频点的利用效率。空闲频点状态的获取取决于卖家探测时间资源的分配,通过设置不同的探测时间,可以达到不同的频谱利用率极限,进而容纳更多的用户。

4 仿真实验与结果分析

4.1 实验配置环境

实验使用随机函数生成买家的业务需求,买家的通信请求时间符合泊松分布,申请的业务时间符合均匀分布,买家通过新接入不同负载条件下的HFCCN,分析TODA-CD 算法性能,买方的信道质量模型和卖方的探测可用频点个数模型遵循随机分布模型。根据武汉垂测站2020年11月7日电离层垂测公开数据,每隔15 min采集一次数据,一天(24 h)的短波可用频段分布如图2所示。由图2可以看出,任意两点可通过武汉地区电离层作为反射点的通信链路,在通信距离不同时可用频段分布不同,在频点拥挤的时段,以3 kHz划分频点,频点个数约为500。

图2 短波可用频段范围随时间变化图(24 h)Fig.2 Variation of available high frequency frequency range over time (24 h)

本实验在频点拥挤情况下进行算法性能分析,在线拍卖过程持续45个周期,每1个周期进行1次网络内频点拍卖,时间长度为15 min。实验参数如表1所示。由于各个属性的随机性较强,运行结果较为曲折,但是并不影响拍卖机制性能分析。

表1 仿真实验参数Table 1 Simulation experiment parameters

在拍卖过程中主要分析了频谱效率(spectrum effectiveness, SE)、切换频次、买家收益3个指标。

4.2 SE

SE是频点使用个数占总频点的比值。当网络负载过重时,冲突增大,传统TODA算法由于不可抢占、不可切换,频谱利用率较低。文献[20]中的Topaz算法和本文提出的TODA-CD算法属于可抢占拍卖算法,能够实现频谱抢占切换,极大地提升了交易成功率。在TODA-CD模型中,由于买家可通过切换、抢占选择空闲频点,理论上而言,只要存在可用空闲频点,必定能够找到空闲频点并进行切换。因此,阻碍频率利用率提高的因素转变为卖家的频谱状态探测能力。由于卖家探测时间资源有限,通过调整卖家模型,分配不同的探测时间,即探测可用频点的数目不同,能够改变网络内频谱利用的上限。仿真分析如图3～图6所示,在不同网络负载条件下,探测最大可用频点个数为2～5时,每条新加入链路拍卖交易的失败率各不相同。可以看出,由于传统TODA不可抢占,在链路随机加入的情况下,每次拍卖中各链路建链成功率不稳定且成功率较低,而TODA-CD算法随着单链路探测时间分配增加,链路最大可用频点数增多,HFCCN的交易成功率上限不断提高且成功率较稳定:当=2时,即每条链路探测感知到2个可用频点,频谱利用率可达到80%;当单链路探测感知可用频点达到5,即=5时,频谱利用率可达到98%以上。卖家中心节点可根据网络系统性能,选择合适的卖家探测资源分配方式,提高系统频谱利用率。

图3 不同频谱利用率下的交易失败率(mf=2)Fig.3 Transaction failure rate at different spectrum utilization rates (mf=2)

图4 不同频谱利用率下的交易失败率(mf=3)Fig.4 Transaction failure rate at different spectrum utilization rates (mf=3)

图5 不同频谱利用率下的交易失败率(mf=4)Fig.5 Transaction failure rate at different spectrum utilization rates (mf=4)

图6 不同频谱利用率下的交易失败率(mf=5)Fig.6 Transaction failure rate at different spectrum utilization rates (mf=5)

4.3 频谱切换

切换频次表明了整个系统的抢占程度以及个体买家对整体系统的影响程度。在保证拍卖成功率的前提下,买家模型通过广度优先搜索生成当前频点与过往频点的同频冲突生成树,对过往冲突进行分析。TODA-CD算法构建了交易频点的冲突拓扑图,如图7所示。其中,每个红点代表一条通信链路,每条连线表示链路频点存在可能冲突,用不同颜色区分冲突树的层数。图7中冲突树共分为4层,涉及30条相关链路,最少切换次数为1,最多切换次数为4,通过计算不同切换方案所产生的买家收益,决定最终的切换方式。

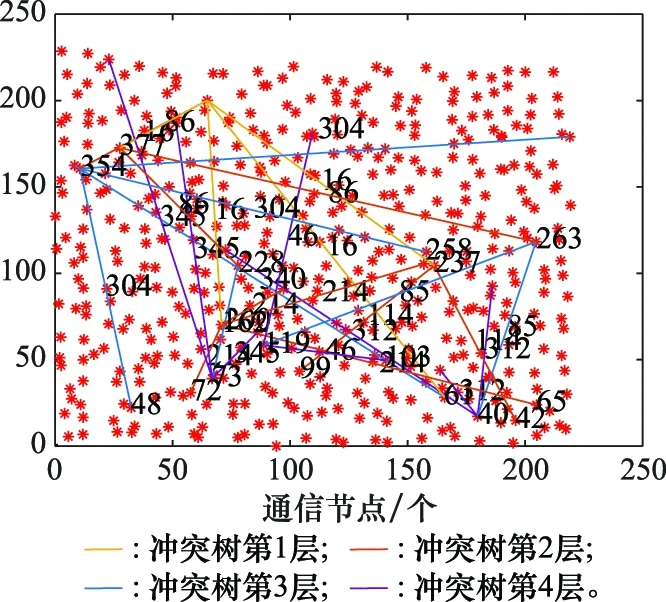
图7 频谱冲突拓扑图Fig.7 Spectrum conflicting topology

在不同的频谱利用率下,随着频谱利用率的提升,传统的Topaz算法的频谱切换次数显著增加。通过模拟10个拍卖周期,得到Topaz和TODA-CD两种算法的平均切换次数,如图8所示。可以看出,在频谱利用率较高的情况下,TODA-CD算法相比Topaz算法能够有效降低网络内切换次数,且分布较为均衡。由于拍卖周期内用户到达和可用频点的随机性,曲线出现部分曲折,可以看出,随着频谱利用率提高,Topaz算法导致切换次数急剧上升,TODA-CD算法能够保持较低的切换次数。

图8 不同频谱利用率下网络内切换次数Fig.8 Intra-network handoff times under different spectrum utilization

在整个在线动态拍卖过程中,通过模拟仿真45个拍卖周期,分析了用户随机到达情况下, 不同网络负载时的网络内频谱切换次数,动态过程如图9～图11所示。可以看出,在SE=0.75,SE=0.85,SE=0.95的状况下,整个动态过程中,TODA-CD算法的切换次数低于Topaz算法,并且保持在一定的范围内波动。部分频点切换次数略高于Topaz算法,是由动态随机接入冲突关系的不同累积导致的。由于采用频分多址的方式进行网络构建,可用频点个数决定了网络的用户承载数量,频谱利用率反映了网络负载情况,图12分析了不同频谱占用率下网络内链路切换次数分布情况,其中“td-0.75”表示在频谱占用率为75%的情况下TODA-CD算法的切换次数。“tz-0.75”表示频谱占用率为75%的情况下Topaz算法的切换次数。可以明显看出,在频谱占用率为75%、85%、95%时,TODA-CD算法切换次数最高为10、10、9,中位数为4、4、5;Topaz算法最高切换次数为27、40、75,中位数为10、18、28,TODA-CD算法切换次数明显低于Topaz算法,同时在频谱利用率发生变化时,切换次数波动维持在一定范围内且明显较少。

图9 动态频谱切换次数(SE=0.75)Fig.9 Dynamic frequency spectrum switching times (SE=0.75)

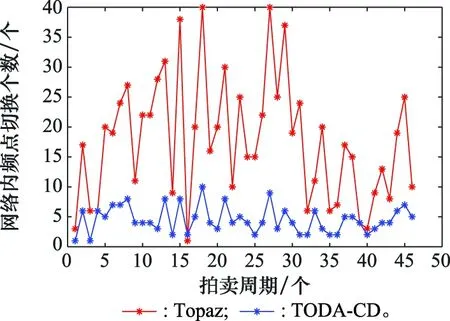
图10 动态频谱切换次数(SE=0.85)Fig.10 Dynamic frequency spectrum switching times (SE=0.85)

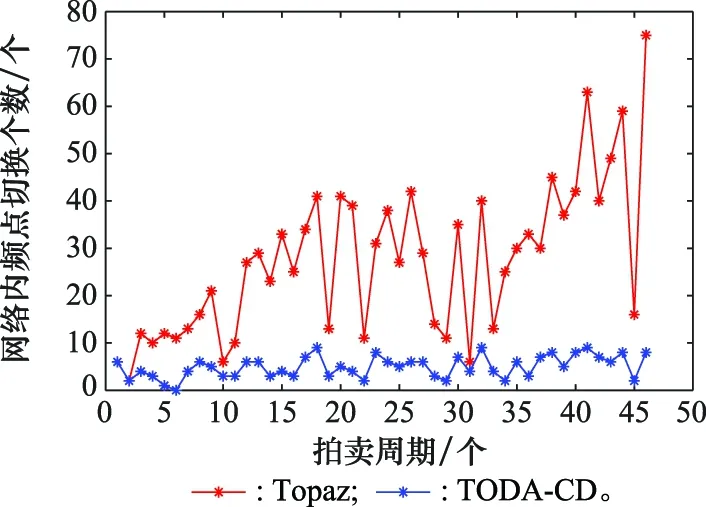
图11 动态频谱切换次数(SE=0.95)Fig.11 Dynamic frequency spectrum switching times (SE=0.95)

图12 不同网络负载情况切换次数分布图Fig.12 Distribution diagram of switching times under different network loads

4.4 卖家收益

在保证拍卖的真实性和公平性的基础上考虑卖家收益最大化。买家收益表明了频点信噪比与用户需求的最优匹配,收益越高,表明整个网络的匹配程度越高。收益对比差异主要取决于惩罚度的不同,即网络系统对于链路频点切换的敏感程度不同。买家收益趋势变化反应了当前动态频谱接入链路的增长或降低的趋势。Limitation门限是网络内单条链路的最优选择组合构成的网络最优选择,是1个理想值。在1%、5%、10%不同惩罚度下,算法收益如图13～图15所示,可以看出,在HFCCN动态接入的过程中,用户收益在不断波动,在运行42个周期后,为0.01、0.05、0.10时,TODA-CD买家收益相比于买家收益极限分别降低了1.29%、2.67%、5.53%。Topaz算法买家收益相比于买家收益极限分别降低了1.89%、4.82、15.32%,在对网络切换敏感的网络中,TODA-CD算法相比Topaz算法优势明显,随着动态过程的持续进行,收益差距进一步拉大,在对网络切换相对不敏感的网络中,TODA-CD算法略优于Topaz算法,买家收益增益相对较少。

图13 动态频谱拍卖买家收益(ζ=0.01)Fig.13 Dynamic spectrum auction buyer revenue (ζ=0.01)

图14 动态频谱拍卖买家收益(ζ=0.05)Fig.14 Dynamic spectrum auction buyer revenue (ζ=0.05)

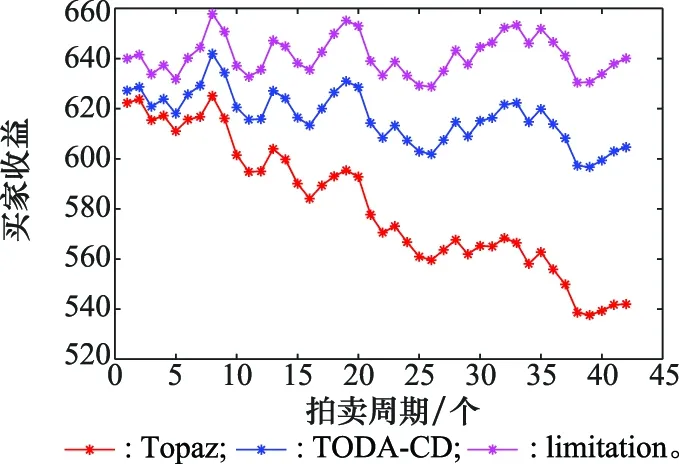
图15 动态频谱拍卖买家收益(ζ=0.1)Fig.15 Dynamic spectrum auction buyer revenue (ζ=0.1)

5 结 论

本文对短波认知电台动态频点接入特性进行了分析,在拍卖过程中,针对高网络负载条件下频点冲突严重的问题,提出了TODA-CD模型。TODA-CD通过构建频点冲突图,构建合适的惩罚函数,完成频点路径切换的最优选择,从而有效降低网络切换次数,提高系统收益。仿真实验表明,本文所构建的在线双拍卖模型相对TODA算法,提高了频谱利用率上限,通过利用冲突图分解算法,在网络高负载情况下切换次数相对Topaz算法明显减少,有效提高了系统收益,具有一定的应用价值。