基于二维正交化WLCLMS的自干扰对消方法

崔中普, 葛松虎,*, 李亚星, 郭 宇, 谢明亮, 孟 进

(1. 海军工程大学军用电气科学与技术研究所, 湖北 武汉 430033;2. 海军工程大学舰船综合电力技术国防科技重点实验室, 湖北 武汉 430033)

0 引 言

在未来,频谱资源的稀缺将成为无线通信领域技术发展最主要的限制因素。全双工通信得益于能够实现同时同频的信号传输与接收,有效提高了现有通信系统的频带利用率,同时也付出了相应的代价。由于发射机和接收机之间有限的隔离度,发射机泄露出来的信号会通过发射天线,经由接收机接收天线耦合进入接收机中,带来严重的共平台自干扰问题。一般而言,耦合的自干扰信号功率相比于正常的接收信号功率高出50～100 dB,将会造成接收机前端饱和甚至烧毁,严重影响有用信号的正常接收。

自适应对消技术能实现全双工系统中共平台自干扰信号的有效抑制,提升通信的可靠性。通常情况下,将射频域对消和数字域对消结合起来以获得最好的自干扰抑制效果。其中,射频域对消器的作用是避免接收链路中诸如低噪放等模拟器件的饱和,使得残余自干扰信号能量在各器件动态范围之内。更为精确的干扰抑制主要由部署于链路中的数字自适应对消器完成。与此同时,最小均方误差(minimum mean square error, MMSE)、最小二乘(least square, LS)、最大似然(maximum likelihood, ML)等准则下的自适应算法被引入数字对消器以实现时变环境下的自干扰信道参数估计,其中最小均方(least mean square, LMS)因结构简单,计算量小,得到广泛应用。

实际环境中,数字对消器性能会受到射频电路中非理想特性的影响。同相/正交相位(in-phase/quadrature-phase， IQ)不平衡,作为一种典型的非理想特性,是指收发链路中,同相支路(I路)和正交相支路(Q路)之间存在幅度和相位上失配。理想情况下,IQ两路应具有相同的幅度、90°相位差。而在实际系统中,非理想的上下变频、滤波器IQ两路的失配,以及信号数字模拟域间相互转换等均会引入IQ不平衡。IQ不平衡的存在将会引入自干扰信号共轭项造成的镜像干扰问题。传统的基于LMS算法的数字对消器难以在抑制自干扰本身的同时消除镜像干扰,造成明显的自干扰残留。针对这一问题,文献[16]提出一种基于广义线性复数LMS(widely linear complex LMS, WLCLMS)的数字域广义线性对消模型,通过增加权向量自由度,实现了自干扰信号及镜像分量的有效抑制。

由于共轭项维度上的拓展,当输入信号具有较强相关性时,WLCLMS会有收敛速度慢、稳态误差大的问题。传统LMS的改进方法主要有变步长LMS、归一化LMS、小波变换LMS、Walsh域变换LMS以及正交变换LMS等。这些方法通过改变步长或实现输入信号时域、频域以及对应变换域上去相关,有效提升了LMS算法收敛速度。相应地,文献[5, 23]给出了一种正交化WLCLMS方法,实现输入信号向量样本时域上去相关,提升了WLCLMS算法收敛速度。

基于文献[5,24],本文提出了一种二维正交化WLCLMS(two-dimensional orthogonalized WLCLMS, TDOWLCLMS)算法。首先,输入信号在时延维度进行正交化,去除了不同信号样本之间的相关性。然后,利用时延去相关输出构造新的信号向量及其共轭项,并通过特征值分解构造正交化矩阵,进一步实现两者间去相关,建立一组彼此间完全不相关的基向量。最后,基于广义线性模型,在数字对消器中利用基向量实现自干扰重构与抑制。同时,本文给出了自适应二维正交化结构以实现时变自干扰信号的实时跟踪。结果表明,TDOWLCLMS算法在有效提升原始WLCLMS收敛速度的情况下,仍能够取得良好稳态误差性能。

1 系统模型

图1为包含有射频对消器和数字对消器两级对消结构的全双工通信模型，其中包含以下内容：数模转换器(digital-to-analog converter, DAC)、低通滤波器(low pass filter, LPF)、可变增益放大器(variable gain amplifier, VGA)、功效(power amplifier, PA)、带通滤波器(band pass filter, BPF)、低噪效(low noise amplifier, LNA)、模数转换器(analog-to-digital converter, ADC)。该模型结构简单,因此被广泛应用于现代无线通信系统中。由多径效应、信号泄露、天线通道反射等产生的自干扰信号首先在射频对消器中完成部分抑制,之后在数字对消器中实现进一步对消。

图1 全双工通信系统结构Fig.1 Architecture of full-duplex communication system

将链路中器件的非理想特性导致的IQ不平衡考虑在内,得到观测到的自干扰信号:

(1)

式中:()=[(),(-1),…,(-+1)]为发送信号向量;()=[(),(-1),…,(-+1)]以及()=[(),(-1),…,(-+1)]为链路信道响应向量;为滤波器阶数;和为IQ不平衡系数矩阵,定义如下:

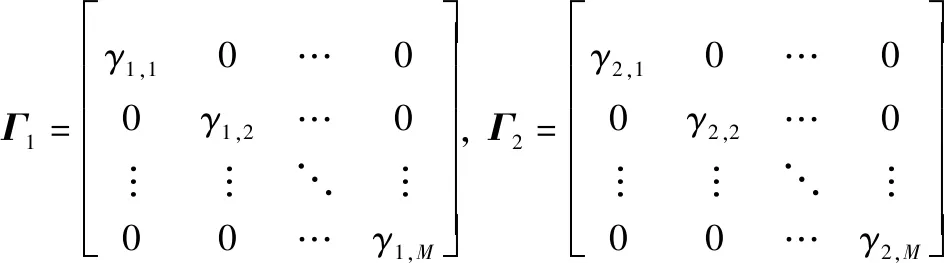
(2)

其中

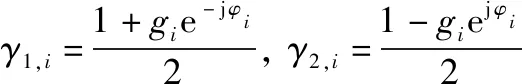
(3)

式中:和分别为IQ两路幅度和相位的失调量,1≤≤。当且仅当=1及=0°时,IQ两路达到了理想的IQ平衡。假设数字对消器得到的信道响应估计为(),则对消后合并输出()为

()=()()

(4)

残差信号()为

(5)

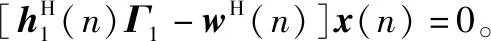
从另一个角度来看,在观测信号()中,IQ不平衡对发送信号序列的作用等价于引入了一个广义线性变换,因而传统的线性数字滤波器模型不再适用。定义广义线性模型下数字滤波器增广输入信号向量为

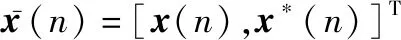
(6)

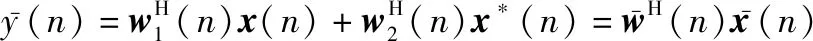
(7)

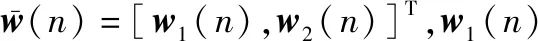
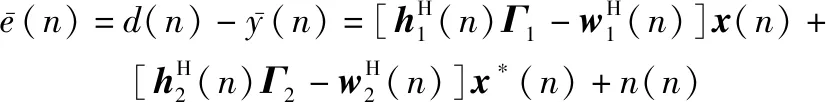
(8)

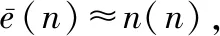
2 复数LMS和WLCLMS

2.1 复数LMS和WLCLMS

LMS算法被引入数字对消器中,实现链路信道响应的自适应更新。全双工通信系统中,在数字域基带实现信号处理,分为IQ两路。因此,LMS算法也对应为复数域实现形式,即复数LMS(complex LMS， CLMS)。传统线性模型下,基于CLMS的数字滤波器合并输出,误差信号及信道响应更新式为

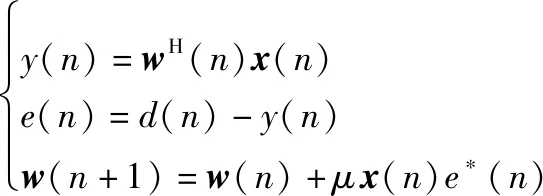
(9)

同理,在广义线性模型下,基于WLCLMS的数字滤波器合并输出,误差信号及信道响应更新公式为

(10)

对比CLMS和WLCLMS可以看到,后者具有两个信道响应权值向量,在计算最终合并输出时提供了更多的自由度。因此,在存在IQ不平衡的情况下,WLCLMS能够取得更准确的干扰信道估计。下面,给出CLMS和WLCLMS两种算法关于收敛速度和稳态误差性能的对比。

2.2 CLMS和WLCLMS的收敛性

(11)

文献[25]通过矩阵分解方法得到两矩阵特征值扩散度和存在如下关系:

(12)

2.3 CLMS和WLCLMS的稳态误差

下面就CLMS和WLCLMS的稳态误差进行对比。假定给出理想的观测参考信号为

(13)

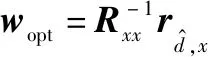
(14)

(15)

则CLMS的最优解可进一步改写为

(16)

对于WLCLMS和CLMS而言,各自MMSE由下式给出：

(17)

当权值向量和取得最优解和时,可以得到两算法稳态误差信号分别为

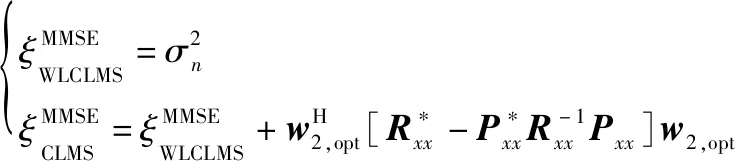
(18)

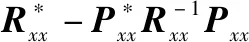
(19)

从式(19)可以知道,WLCLMS算法相较于CLMS算法,能取得更为优异的稳态误差性能。

3 TDOWLCLMS

3.1 数学模型

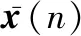
输入增广信号矢量为

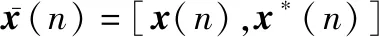
(20)

对自相关矩阵=E{}做特征值分解,可得

=

(21)

式中:为对角矩阵,主对角线元素为的特征值,并按照由大到小的顺序排列;为由特征值对应的特征向量构成的酉矩阵。则可得正交化矩阵为

=-12

(22)

进一步可得正交化后的输入信号向量为

()=[(),(),…,()]=()

(23)

并且满足

E{()()}=

(24)

定义()如下:

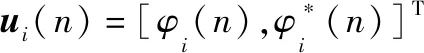
(25)

进一步做正交变换,可以得到

()=2,()=()

(26)

式中:正交化矩阵可通过对()自相关矩阵做特征值分解得到,类似于的获取方式。

定义新的输入信号向量()为

()=[(),(),…,()]

(27)

基于新的输入信号向量(),得到数字滤波器合并信号:

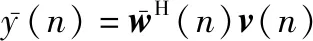
(28)

信道响应权值向量更新式为

(29)

算法1 TDOWLCLMS参数 滤波器阶数M;步长因子μ;满足0<μ<1/λmax。输入 传输信号x(n);观测信号d(n)。输出 误差信号e-(n)。1步骤1 输入信号增广矢量正交化2forn=M,M+1,…,Ndo3 x(n)=[x(n),x(n-1),…,x(n-M+1)]T;4 Rxx=x(n)xH(n);5end6Rxx=1N∑Nn=Mx(n)xH(n);7Rxx=KΣKH;8Q1=Σ-1/2KH;9forn=M,M+1,…,Ndo10 φ(n)=[φ1(n),φ2(n-1),…,φM(n)]T=Q1x(n);11 φ～(n)=[φ1(n),φ∗1(n)]T;12 Rφ～=φ～(n)φ～H(n);13end14Rφ～=1N-M+1∑Nn=MRφ～(n);15Rφ～=K1Σ1KH1;16Q2=Σ-1/21KH1;17步骤2 基于LMS算法自适应对消18forn=N+1,N+2,…,do19 x(n)=[x(n),x(n-1),…,x(n-M+1)]T;20 φ(n)=[φ1(n),φ2(n-1),…,φM(n)]T=Q1x(n);21 fori=1,2,…,Mdo22 ui(n)=[φi(n),φ∗i(n)]T;23 vi(n)=Q2ui(n);24end25 v(n)=[v1(n),v2(n),…,vM(n)]T;26 w-=0;27 e-(n)=d(n)-w-H(n)v(n);28 w-(n+1)=w-(n)+μv(n)e∗(n);29end

3.2 TDOWLCLMS的收敛和误差性能

下面分析TDOWLCLMS算法的收敛特性与稳态误差。首先,给出新的输入信号向量()自相关矩阵为

(30)

(31)

可以看到,二维正交化使得白化为单位矩阵,因而其特征值扩散度为1,与CLMS以及WLCLMS算法对应矩阵特征值扩散度关系为

(32)

其次,假设此时理想的参考信号为

(33)

二维正交化WLCLMS算法与传统WLCLMS算法一样,增加了权值向量自由度,同时利用输入信号向量本身及共轭项来估计合并输出信号。此时,MMSE表达式为

(34)

当算法达到收敛时,稳态误差信号为

(35)

基于上述分析可以看到,二维正交化WLCLMS在有效提升了传统WLCLMS的收敛速度的同时保持了良好的稳态误差性能。

3.3 TDOWLCLMS的自适应实现

第31节给出的二维正交化方法,实现了输入信号向量在时域样本以及自身共轭项之间的正交化。然而,从算法伪码中可以看到,在求解正交化矩阵和的过程中,需要一定数量的输入信号训练样本,在实际通信系统中,会引入较大的延迟。与此同时,当干扰信道出现波动时,需要利用新的信号样本来重新计算正交化矩阵和的值,不利于时变干扰信号的跟踪。因此,本文给出了一种自适应的二维正交化结构,以适应快速变化的无线通信环境。

图2给出了自适应二维正交化算法原理框图。

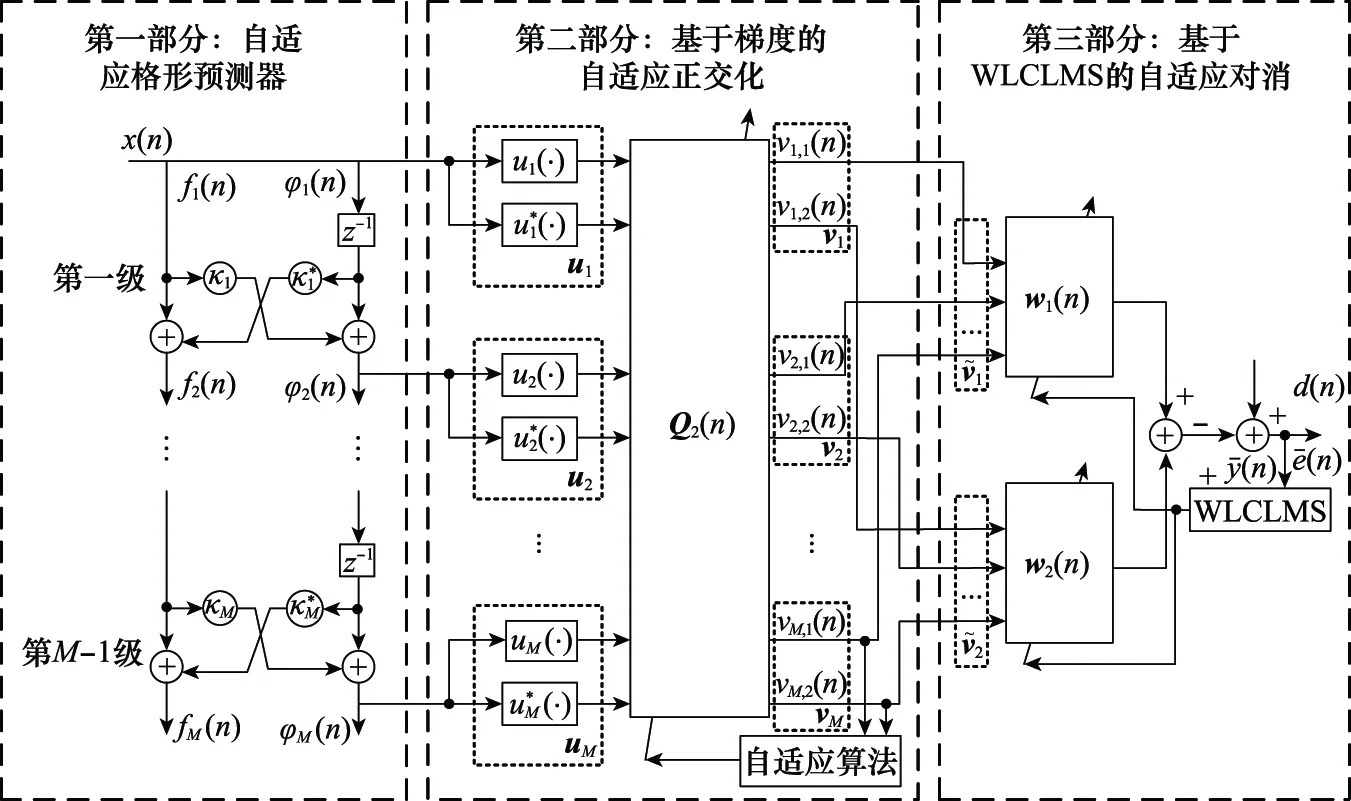
图2 自适应二维正交化处理结构框图Fig.2 Block diagram of the adaptive two-dimensional orthogonalization processing architecture

可以看到,整个结构分为3个部分:第一部分为一个阶梯度自适应格型预测器(gradient adaptive lattice predictor, GALP),用来实现输入信号向量不同时延样本之间的正交化。整个基于GALP的正交化过程可以表示为

(36)

式中:()和()分别为时刻第个节点前向及后向预测误差;是一个介于0和1之间的正常数参数;-1()则表示到时刻为止,阶前后向预测误差能量之和。=-1()表示归一化步长因子,用来控制反射系数在每一次迭代中的调整量。式(36)中各参量初始化值设置为

(37)

其中,c为一个值非常小的正常数。

第二部分为自适应白化算法,实现信号与共轭项间正交化,采用基于梯度的自适应方式进行正交化矩阵的更新。构造如下代价函数:

(38)

将代价函数关于求偏导,可得

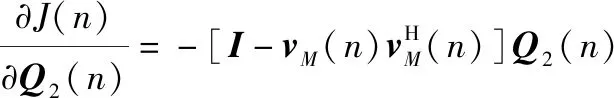
(39)

得到关于的自适应更新公式为

(40)

式中:为自适应迭代步长。

第三部分为自适应对消,通过新构建的输入信号向量(),采用广义线性模型,实现干扰信号信道参数的自适应估计与调整更新。数字滤波器合并输出,误差信号以及信道参数权值向量自适应更新公式为

(41)

式中:为权值更新迭代步长。可以看到,前两级实现了输入信号向量在时域和共轭项上二维自适应正交化,第三级则利用正交化的信号实现自适应自干扰对消。自适应二维正交化结构满足了时变环境中快速变化干扰信道的实时跟踪要求。

4 仿真结果与分析

基于Matlab平台对所提出TDOWLCLMS性能进行验证,并与其他算法进行对比,仿真结果为50次蒙特卡罗实验的平均。输入信号为功率0 dB的正交相移键控(quadrature phase shift keying, QPSK)信号,高斯白噪声功率设置为-30 dB,式(5)中链路信道响应向量设置为()=()=[1,1,…,1]。对所有的算法而言,迭代步长统一设置为=0001。我们的目标是通过发送数据重构自干扰信号以实现自干扰信号的对消,为了仿真的简便性,假设有用信号和干扰信号互不相关,因此未将有用信号考虑在内。在仿真过程中,主要分析带宽和采样频率、滤波器阶数以及IQ不平衡量对4种算法对消性能的影响。

4.1 不同算法下对消前后频谱

图3为对消前以及4种算法下对消后残余干扰信号频谱。图3(a)和图3(b)分别对应2 MHz带宽以及10 MHz带宽QPSK信号对消前后频谱图,此时系统采样率为20 MHz,滤波器阶数为5,IQ不平衡量设为=095且=5°。可以看到,相比原始干扰信号频谱,4种自适应算法均实现了自干扰信号的有效抑制。就CLMS算法而言,其未能实现自干扰信号完全抑制,存在一定的镜像干扰残留。WLCLMS和正交化WLCLMS两种算法实现了干扰信号本身和镜像分量的同时抑制,但仍然存在部分残余。其中,过采样条件下的2 MHz带宽QPSK信号由于自身间较强的相关性,干扰残留相比于10 MHz带宽QPSK信号更多。而TODWLCLMS实现了将自干扰信号对消至接近底噪的抑制效果。

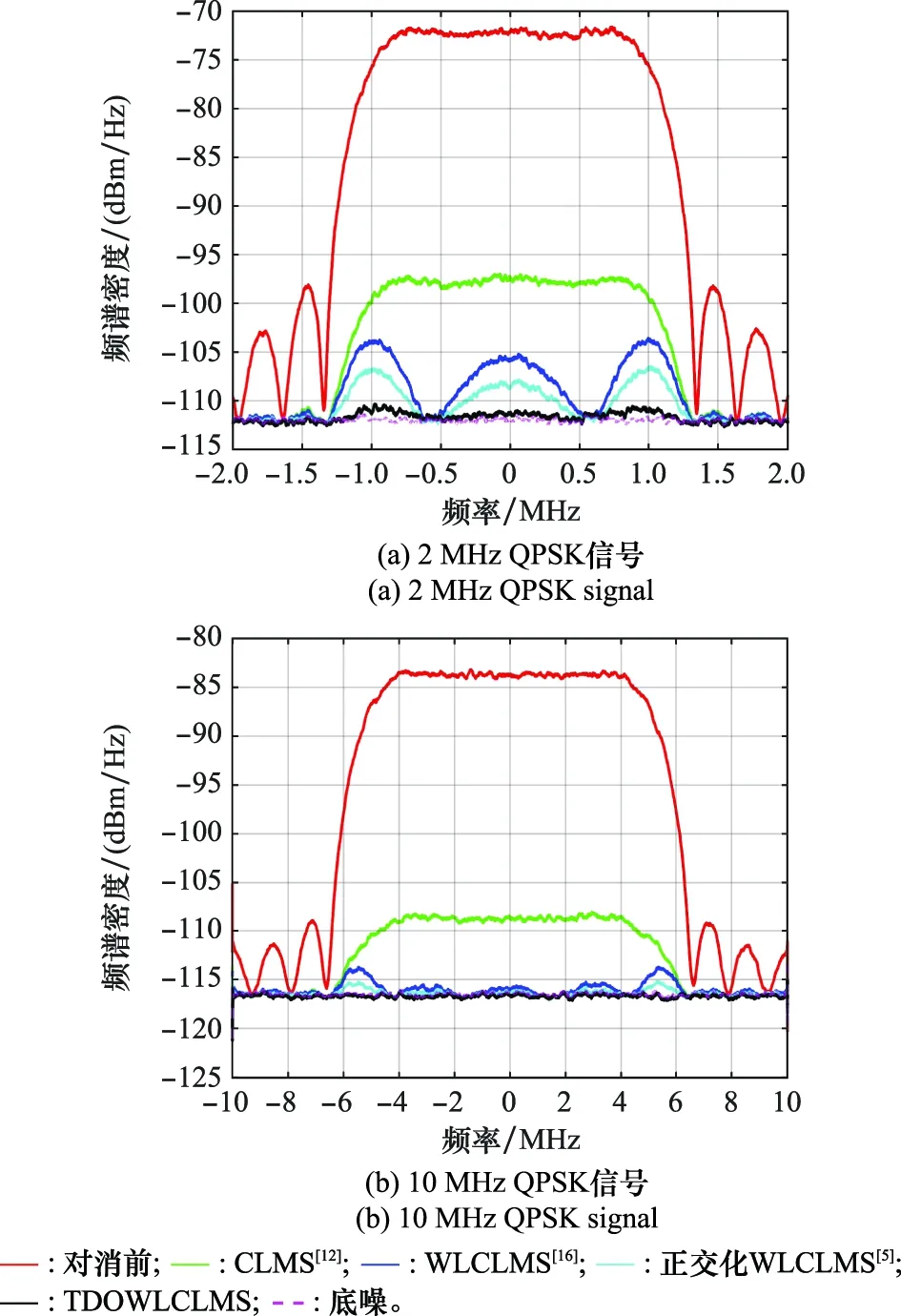
图3 对消前后频谱分析Fig.3 Power spectrum density analysis before and after cancellation

4.2 不同算法下误差信号功率

图4为不同算法下误差信号功率随迭代次数变化曲线。图4(a)和图4(b)分别对应2 MHz带宽以及10 MHz带宽QPSK信号。可以看到,相较于CLMS算法,WLCLMS算法有着较小稳态误差,但收敛速度较慢。正交化WLCLMS在保持较小稳态误差的同时,提升了收敛速度。而TDOWLCLMS进一步提升了收敛速度,同时有着最优异的稳态误差性能。2 MHz带宽QPSK信号由于自身间较强的相关性,4种算法下整体收敛速度相较于10 MHz带宽QPSK信号稍慢一些。

图4 收敛速度分析Fig.4 Convergence rate analysis

4.3 采样率对算法收敛速度的影响

图5为不同算法下2 MHz 带宽QPSK在不同采样率下误差信号功率随迭代次数的变化曲线,此时滤波器阶数为5,IQ不平衡量设为=095且=5°。我们知道,对于非周期平稳随机过程而言,采样样本间隔越小,则两个样本之间的相关性越强。极端情况下,当样本间隔趋于无穷大,则意味着两样本完全不相关。可以看到,随着采样频率变大,样本间相关性变强,4种算法收敛速度均存在一定程度的下降。对于CLMS算法而言,采样率增加一倍,达到收敛所需迭代次数也增加一倍。而对WLCLMS,所需迭代次数增加一倍以上。正交化WLCLMS相较于WLCLMS减少了收敛所需迭代次数。而TDOWLCLMS收敛速度受采样频率变化影响最小,仍然有着最快的收敛速度,表现出较强的鲁棒性。

图5 不同采样率下收敛速度分析Fig.5 Convergence rate analysis with respect to different sampling frequency

4.4 滤波器阶数对算法收敛速度的影响

图6为不同算法下,滤波器阶数对收敛速度的影响。输入为2 MHz带宽QPSK信号,采样率为10 MHz,IQ不平衡量设置同第4.3节。正如前面的分析,算法收敛特性与输入信号自相关矩阵特征值扩散度有关,滤波器阶数会改变自相关矩阵特性。当滤波器阶数增加时,可以看到,WLCLMS算法受滤波器阶数影响最为明显,随着滤波器阶数增加,达到收敛所需迭代次数也在增加。正交化WLCLMS减少了收敛所需迭代次数。CLMS与TDOWLCLMS受滤波器阶数变化影响最小。一般而言,需要一定数量的滤波器阶数以实现对信号较为准确的拟合,因此TDOWLCLMS相较于其他3种算法,具有更高的适用性。

图6 不同滤波器阶数下收敛速度分析Fig.6 Convergence rate analysis with respect to different filter order

4.5 IQ不平衡失调量对算法收敛速度的影响

图7为IQ不平衡量对4种算法对消误差信号的影响。滤波器阶数为5,采样频率为10 MHz,输入为2 MHz带宽QPSK信号。其中,={k,k,…,k}为共轭项系数,用来调节其在整个输入信号中的比重,原始信号项系数固定为=diag{1,1,…,1}。通过仿真结果可以看到,随着共轭项系数的增加,4种算法在达到收敛状态时,稳态误差信号均有所增大。其中CLMS受影响最为严重。与此同时,TDOWLCLMS在取得最小稳态误差的同时,始终保持着最快收敛速度,从另一方面说明其鲁棒性。

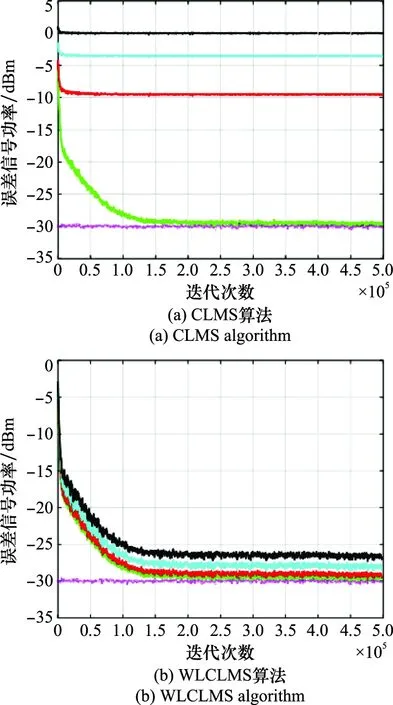
图7 不同IQ不平衡量下收敛速度分析Fig.7 Convergence rate analysis with respect to different IQ imbalance quantity

5 结 论

本文提出了一种TDOWLCLMS算法,将输入信号向量在样本延时以及共轭项两个维度上进行正交化,实现了输入信号向量完全的去相关。有效解决了传统WLCLMS算法虽然有着较好稳态误差性能但存在收敛速度慢的问题。仿真结果表明:TDOWLCLMS有着将干扰信号对消至接近底噪的抑制能力,在取得优异稳态误差的同时,有效减少了收敛所需迭代次数。此外,TDOWLCLMS算法受系统采样率、滤波器阶数、IQ不平衡量变化的影响较小,展现出良好的鲁棒性。与此同时,给出了TDOWLCLMS算法的自适应结构,实现了时变环境中自干扰信号的实时跟踪,具有较强工程实践意义。后续将对如何在快速收敛条件下有效提升信干比进行进一步研究。