Ka频段合成孔径雷达高度计机载数据处理

刘晓楠, 王 昆, 孙晗伟, 鲁耀兵

(北京无线电测量研究所, 北京 100854)

0 引 言

海洋覆盖了地球表面积的70%以上,对人类和自然界有巨大影响。然而与陆地相比,人类对海洋的认知远远不够。在空间科学发展以前,人类只能通过舰船对海洋进行局部观测;随着卫星遥感技术的快速发展,人类对海洋的探索进入了新纪元。

雷达高度计是一种重要的微波遥感器,它可以对海洋进行全球尺度的连续监测。通过对海面回波进行重跟踪,雷达高度计可以测量海表面高度、有效波高、后向散射系数等关键参数。这些数据可应用于地球物理学、海洋动力学、大气环境学、海冰检测等方面,对军事领域的重力场反演和民用领域的灾难预警具有深远意义。

传统雷达高度计工作于实孔径模式,其主要缺点有:脉冲有限足迹直径大,公里级的分辨率难以满足现阶段的海洋观测需求;发射功率浪费大,大部分功率都在脉冲有限足迹之外;回波信噪比低,测距精度难以提高。

目前,合成孔径雷达(synthetic aperture radar, SAR)高度计已经成为新一代雷达高度计,其显著优势有:通过引入合成孔径技术,使沿轨向分辨率大大提高,分辨率由公里级提升至百米级;通过延迟补偿技术,利用了天线波束内的全部能量,降低了发射信号的峰值功率;通过多视处理,提高了有效观测次数,使测距精度大幅提高。

Cryosat-2卫星于2010年发射,其高度计载荷首次试验了合成孔径工作模式。Sentinel-3A卫星于2016年发射,其高度计载荷首次在全球尺度上业务化运行合成孔径模式。2020年11月21日,Jason-CS/Sentinel-6任务发射了第一颗卫星S6 Michael Freilich(S6-MF),其主载荷Poseidon-4也是一颗SAR高度计。

相比于Ku频段,Ka频段具有更高的信噪比和分辨率,且不需要使用Ku和C双频段来进行电离层校正,因此越来越多的高度计开始工作于Ka频段。比如2013年发射的SARAL/AltiKa卫星,其主载荷是一颗Ka频段高度计,其测量性能已被证实优于传统Ku频段高度计;以及计划于2022年发射的SWOT卫星,其主载荷也是一颗Ka频段高度计。

综上,Ka频段SAR高度计是未来高度计卫星发展的方向之一,十分有必要对其进行研究。但是,选择Ka频段也会带来令人担忧的问题,比如,由于频段升高而带来的雨衰,是否大幅影响数据的有效率,由于波束变窄使得回波受波浪影响更大,导致回波形状发生变化,在此情况下模型的适应性和重跟踪的成功率又将如何等。

因此,面对这些未知问题,进行前期机载试验尤为重要。本文所基于的机载试验,是国内首次Ka频段SAR高度计海面机载试验。本文利用试验数据,基于一种改进的回波模型,成功实现了海面高度反演,并且通过模型数据对反演参数进行了定性验证,结果非常吻合。但是,由于高海况下飞机不具备起飞条件,因此很难获取相应数据。所以机载试验只能验证中低海况,有其局限性。

1 SAR高度计回波预处理

1.1 高度计原理概述

雷达高度计主要用来测量目标相对于椭球参考面的高度。如图1所示,对于被观测目标,当高度计在其正上方点时,已知卫星相对于椭球参考面的轨道高度为,测量得到高度计与海面之间的距离为,则目标相对于椭球参考面的高度为

Δ=-

(1)

SAR高度计不仅在被观测目标的正上方位置点进行观测,还在轨道上的多个位置如、点对目标进行观测。通过多次测量进行多视处理,提高测量精度。根据定义,在偏离被测目标正上方时测得的距离不能直接作为测量结果,所以在多视处理前需要进行延迟距离校正。

图1 高度计测高原理图Fig.1 Schematic of height measurement of altimeter

雷达高度计向星下点发射脉冲,图2是高度计足迹的俯视图。随着时间推移,脉冲照明区由逐渐增大的圆形变为内环逐渐扩大的圆环,直至天线波束边缘。其中,沿轨向为卫星飞行方向,交轨向为观测表面垂直于沿轨向的方向。

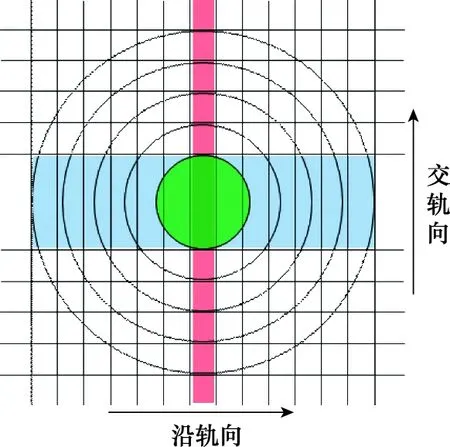
图2 高度计足迹示意图Fig.2 Diagram of altimeter footprint

传统高度计采用实孔径,其脉冲有限足印定义为面积最大的圆形照明区,如图2中绿色圆形所示。足印半径与脉冲有限宽度有关:

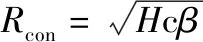
(2)

式中:是轨道高度;c是光速;=1,是发射信号带宽。

在SAR高度计中,雷达首先以较高的脉冲重复频率(pulse repetition frequency, PRF)发射一簇相干脉冲,然后等待接收脉冲。接收完这一簇脉冲后,再发射下一簇脉冲。

SAR高度计在接收到脉冲簇回波后,首先进行去斜处理,以实现脉冲压缩。然后,利用簇内脉冲的相干性,进行合成孔径处理。通过多普勒波束锐化,在沿轨向形成多个多普勒条带,如图2中粉色区域所示。经过延迟距离校正,将不同子视回波前沿对齐。最后进行多视处理,获取用于回波重跟踪和参数反演的回波。

综上,SAR高度计数据处理的关键技术主要包括:多普勒波束锐化、延迟距离校正、子视回波配准、多视处理、回波建模、回波重跟踪。其中,回波建模和重跟踪方法将在第2节进行介绍,将前面4项称为回波预处理。

1.2 多普勒波束锐化

在脉冲簇模式下,完整的合成孔径过程被划分为多个子孔径合成过程,每一个脉冲簇对应一个子孔径;相应地,数据处理也以脉冲簇为单位进行。

通过子孔径内的合成处理,雷达等效波束变窄了。称等效后的窄波束为子波束,每个子波束覆盖一个多普勒条带,如图2中粉色区域所示,条带的宽度决定了沿轨向分辨率。

设子波束宽度为,则

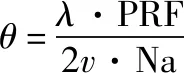
(3)

式中:是波长;是卫星速度;Na是簇内脉冲数。

设雷达高度计正下方子波束对应的多普勒条带宽度为,则

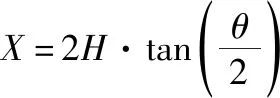
(4)

对于偏离雷达正下方的子波束对应的条带,其宽度根据几何关系略有增加,一般为厘米级,可忽略不计。

传统高度计的沿轨向分辨率就是其有限足印的直径,一般为公里级。而SAR高度计的沿轨向分辨率是多普勒条带的宽度,一般为百米级。因此,SAR高度计能够大大提高沿轨分辨率。

另外,通过延迟距离校正,SAR高度计可以积累更多的信号能量,如图2中蓝色区域所示;而传统高度计只能积累脉冲有限足迹内的能量,如图2中绿色区域所示。因此,SAR高度计的信噪比更高,相应测高精度也得到提高。

每个雷达回波由波束覆盖范围内所有条带产生,由于卫星具有水平速度,所以沿轨向不同条带产生的回波具有不同的多普勒频率。形象地来看,高度计的天线波束在沿轨向被锐化成多个子波束,天线的照射区域被锐化成多个条带,如图3所示,上述过程就是多普勒波束锐化。

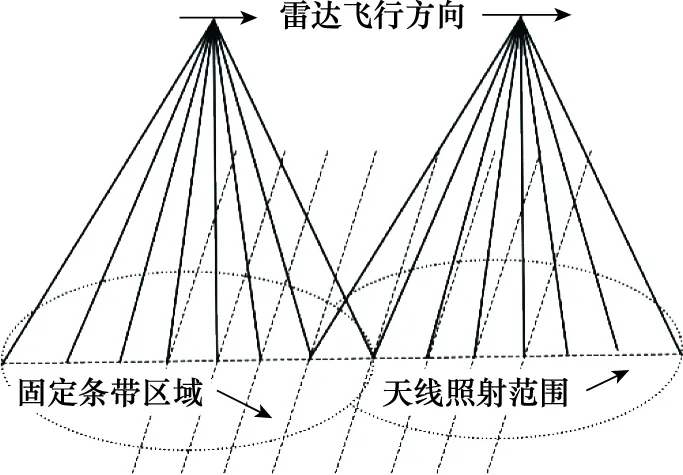
图3 多普勒波束锐化示意图Fig.3 Diagram of Doppler beam sharpening

1.3 子视回波配准

设某脉冲簇中间时刻雷达的沿轨向坐标为,发射该脉冲簇时波束覆盖范围内某条带的沿轨向中心坐标为,则该条带回波的多普勒频率为

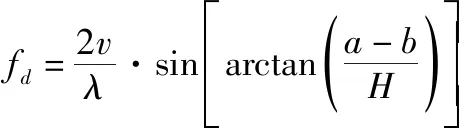
(5)

定义距离向为雷达接收脉冲的方向,方位向对应沿轨向。将距离向脉冲压缩后的数据进行方位向傅里叶变换,得到距离-多普勒域的二维回波数据,则基于式(5)求得的多普勒频率可以提取出属于某一条带的回波,称为该条带的一个子视回波。

如图3所示,随着卫星飞行,雷达将在轨道上的多个位置对某一条带区域使用不同的子波束进行多次观测,得到多个子视回波。将子视回波与沿轨向条带进行对应的过程,就是子视回波配准。

在观测过程中,对某一固定条带,雷达有一个先靠近再远离的过程。因此,在距离-多普勒域,属于同一条带的不同多普勒频率的子视回波前沿在方位向的排列是一条抛物线。

1.4 延迟距离校正

多视处理,是将属于同一条带的子视回波进行非相干叠加,通过多次测量求取平均值,提高测量精度。然而,由第13节可知,各子视回波前沿在方位向的排列是一条抛物线,不能直接累加。因此,必须先进行延迟校正,将子视回波的前沿对齐。

将一组脉冲簇回波数据变换到距离-多普勒域,不同多普勒频率的子视回波属于不同观测条带,它们的回波前沿在方位向的排列同样是一条抛物线。先在脉冲簇内进行距离校正,将子视回波前沿对齐,进而根据条带位置提取对应的子视回波,即进行子视回波配准。

脉冲簇内的距离校正可以采用在距离频域进行相位补偿的方式(方位向在多普勒域)。对于多普勒频率为的回波,其校正量近似为

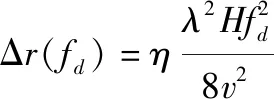
(6)

式中:为地球曲率。

令距离频率为,则相位补偿量为

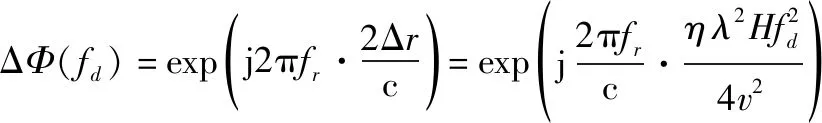
(7)

对所有脉冲簇进行延迟距离校正和子视回波配准后,属于某条带的子视回波前沿已经对齐。将所有子视回波进行非相干叠加,就得到了多视回波。

2 SAR高度计回波重跟踪

2.1 改进的回波模型

1977年,Brown基于一些假设条件,提出了海面后向散射回波模型的经典表达式:

()=()*()*()

(8)

式中:符号*表示线性卷积;()是接收回波的平均功率函数,可以表示为3项函数的线性卷积:()是平坦海面的脉冲响应函数;()是海面镜像点的概率密度函数;()是雷达系统的点目标响应函数。

在理想情况下,雷达高度计波束应该指向星下点。但是由于卫星平台的姿态控制精度有限,实际雷达波束指向可能与星下点方向存在偏差。误指向角即为实际波束指向与星下点方向的夹角。当存在误指向角时,天线方向图就会发生变化,进而影响平坦海面的脉冲响应函数。

在合成孔径模式下,沿轨向分辨率从公里级提升至百米级,因此回波模型对天线方向图和误指向角更加敏感。但是,由于几何模型本身已经非常复杂,且含有大量卷积运算,因此目前现有的模型大多忽略了对误指向角的考虑,这将在一定程度上影响参数估计的精度。

文献[25]提出了一种含有误指向角的SAR干涉高度计回波模型。本文在此基础上,通过将该文信号模型中的干涉基线长度设置为0,并结合几何关系对模型做相应处理,将其转换为一种可以适用于底视SAR高度计的回波模型。

这种改进的回波模型将误指向角作为输入量,可以充分利用星上设备测量的平台姿态角,提升模型与实际回波的匹配程度,进而提高参数反演的精度。

本文回波模型基于3项卷积模型。其中,海面散射点的概率密度函数表达式如下:

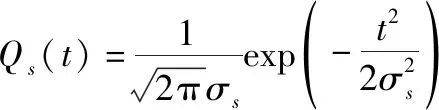
(9)

雷达系统的点目标响应函数表达式如下:

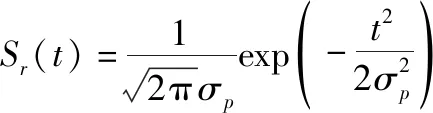
(10)

以上两项函数的卷积结果为

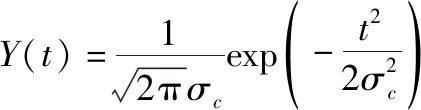
(11)

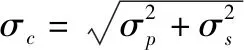
(12)

式中:混合波高=SWH/2c,SWH为有效波高;点目标响应的3 dB宽度=1.125/B。

建立回波模型的重难点在于确定平坦海面的脉冲响应函数()。该部分建立的思想为:首先根据多普勒频率,建立每个多普勒分辨条带的单视脉冲响应函数,然后结合式(11)进行卷积计算,生成单视回波模型,最后进行多视处理。

在高度计2D足迹平面上,设海面散射点与星下点连线相对于卫星飞行方向的夹角为ϑ,则第个合成子波束的脉冲响应函数表达式为

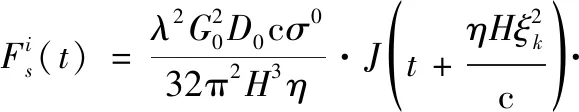
(13)

式中:

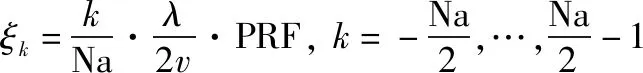
(14)

(15)

=cos ϑ-

(16)

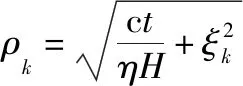
(17)

式(13)～式(17)涉及的参数和函数有:天线增益;合成波束增益;后向散射系数;阶跃函数(·);波数。

(·)为含有误指向角的天线方向图,其近似表达式为

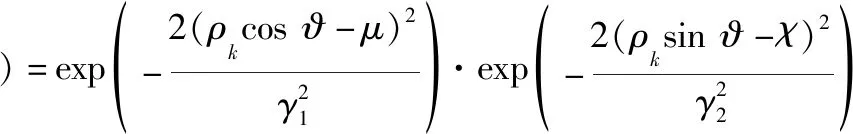
(18)

式中:为俯仰角;为横滚角;和分别为沿轨向和交轨向的波束宽度。俯仰角和横滚角共同构成误指向角。需要指出的是,式(18)未考虑偏航角,因为偏航角只影响高度计观测的地表位置,不影响天线方向图的能量分布和回波形状。

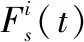
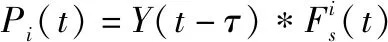
(19)

式中:()的定义见式(11)。

若总积累视数为,则多视回波值为

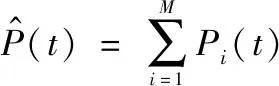
(20)

至此已经建立了完整的回波模型。当其他系统参数确定时,式(8)的回波模型可以抽象为3个参数的表达式:

()=(,SWH,)

(21)

图4展示了SAR高度计回波模型随回波前沿、有效波高、回波幅度、误指向角的变化。

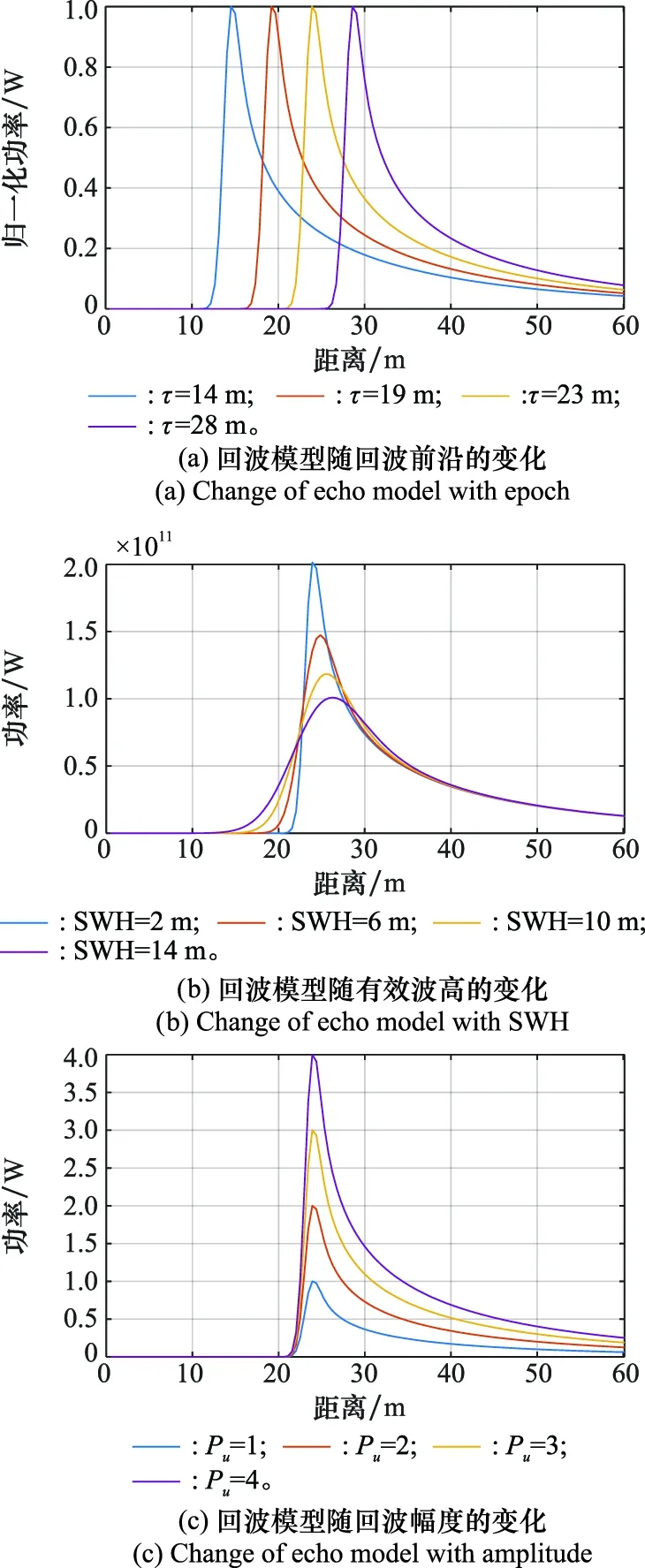
图4 SAR高度计回波模型Fig.4 SAR altimeter echo model

需要说明的是:对于回波前沿,由于回波的时间分辨单元为纳秒级,为便于显示,在图4(a)中利用光速将回波前沿的单位转换为m;另外,由于俯仰角和横滚角共同构成误指向角,为了便于说明,在图4(d)中,仿真时取俯仰角为0°,即误指向角等于横滚角。

2.2 最小二乘重跟踪

回波重跟踪是采用一定的算法,使第2.1节中的回波模型式(21)与实际回波估计式(20)达到最吻合的状态,从而得到回波中蕴含的反演参数。

在实际应用中,通过对高度计回波进行重跟踪,可以得到抽象模型式(21)中的回波前沿、有效波高和回波幅度,即(,SWH,)。

基于回波前沿,可以计算出高度计到观测表面的距离,进一步反演海面高度,监测气候变化;基于有效波高SWH,可以推测此时的海况,对于舰船航行有重要意义;基于回波幅度,可以计算后向散射系数,进一步反演海面风速。

本文采用最小二乘算法进行回波重跟踪,其基本思想是使回波模型与实际回波的误差平方和最小。在具体实现时,采用迭代的方法获得最优解。

首先将SAR高度计回波模型式(21)简写为3项待估参数的表达式:

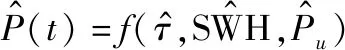
(22)

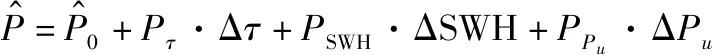
(23)

式中:(Δ,ΔSWH,Δ)是各参数的增量;(,,)是模型对各参数的偏导数:

(24)

令为回波的第个采样值,回波共有个采样点,则误差方程为

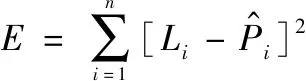
(25)

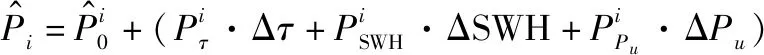
(26)

令对各参数的偏导数为0,矩阵表示为

=

(27)

式中:是回波模型的偏导数矩阵;是残差矩阵;是待估参数的增量矩阵。

求解式(27),得至矩阵,更新待估参数:

(28)

重复上述步骤,直至回波模型与实际回波足够接近,即可停止迭代,此时便得到了反演参数。

3 Ka频段机载数据处理

3.1 机载试验简介

2019年,在中国山东青岛海域获取了Ka频段SAR高度计的机载校飞试验数据,飞行航线如图5中的绿色线段所示。

图5 机载试验航线Fig.5 Airborne experiment route

在机载试验中,雷达以5 kHz的PRF均匀收发脉冲,该PRF可以保证脉冲之间具有相干性,因此可以脉冲簇为单位,进行合成孔径处理。

机载试验主要参数如表1所示。

表1 机载试验参数Table 1 Parameters of airborne experiment

3.2 机载回波预处理

在机载试验中,飞机姿态变化幅度比较剧烈,因此首先需要对回波数据进行运动补偿,并做去斜处理,以实现脉冲压缩。然后以64个回波为一簇,进行延迟距离校正,经过子视配准和多视处理后,获取合成孔径模式下的多视回波。

图6和图7展示了延迟距离校正前后,距离-多普勒域的脉冲簇回波,可以看到校正后不同子视回波的前沿已经对齐。

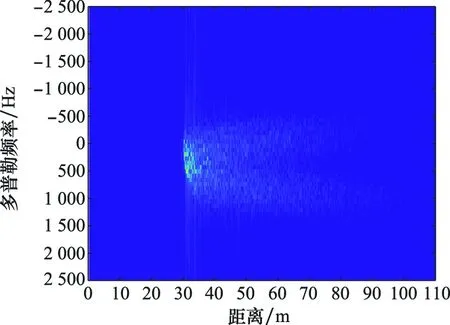
图6 距离校正前的脉冲簇回波Fig.6 Pulse cluster echo burst before range correction

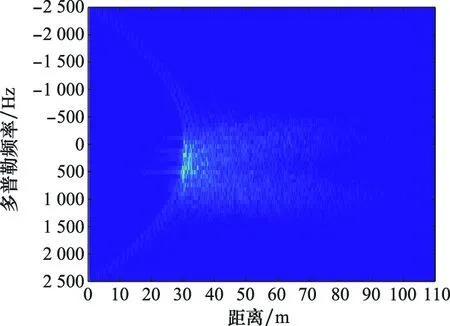
图7 距离校正后的脉冲簇回波Fig.7 Pulse cluster echo after range correction

图8中红色曲线展示了一个典型的归一化多视回波,即对回波幅度进行归一化处理,便于后续的回波重跟踪;蓝色曲线展示了一个典型的归一化脉冲簇回波,可以看到多视处理极大地提升了回波信噪比。

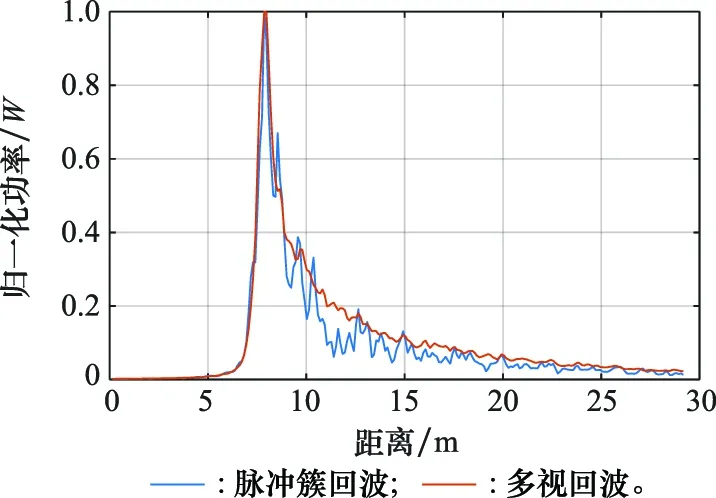
图8 归一化多视回波和脉冲簇回波Fig.8 Normalized multi-view echo and pulse cluster echo

需要说明的是:为了更清晰地显示回波细节,对原始回波进行了截取,因此图8及以后的图示中,回波的距离位置与图6和图7不同。

图9展示了机载SAR高度计的448个多视回波序列。

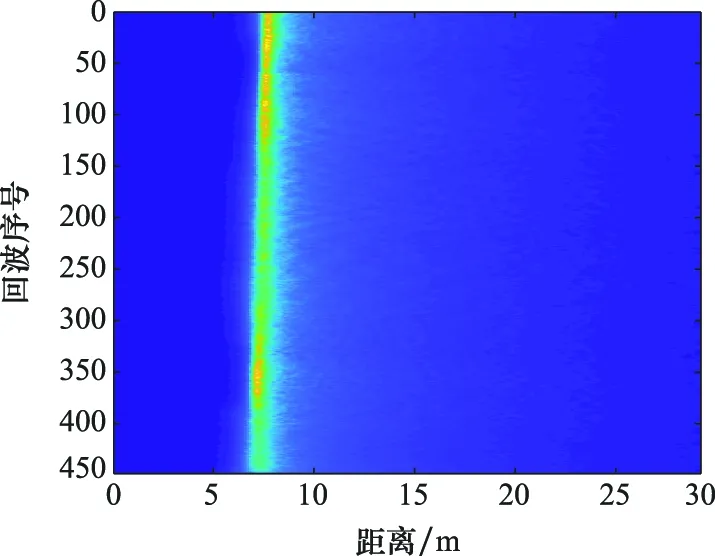
图9 机载多视回波序列Fig.9 Airborne multi-view echo sequence

3.3 机载回波重跟踪

根据机载试验系统参数建立SAR高度计回波模型,对每一条多视回波进行重跟踪。

在建立模型时,充分利用了由惯导设备测量的飞机姿态角信息,将其作为回波模型的误指向角输入,从而使回波模型更接近真实的回波,便于在重跟踪时快速收敛。

图10展示了一个归一化多视回波的重跟踪过程,其中深蓝色曲线为归一化机载回波,红色曲线为初始回波模型,黄色曲线、紫色曲线、绿色曲线、浅蓝色曲线分别为第1、2、3、14次迭代后的回波模型。可以看到,随着迭代次数增加,回波模型与机载回波逐渐逼近。

图10 回波重跟踪过程Fig.10 Echo re-tracking procedure

图11展示了对应的重跟踪结果。由图11可以看到,当引入误指向角时,回波估计与实际机载回波吻合得更好,因此参数估计更加准确。

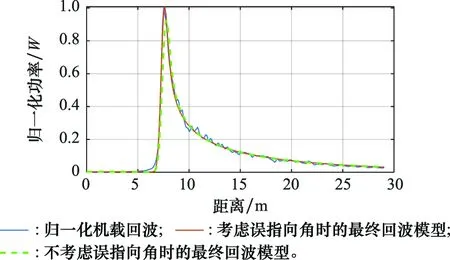
图11 回波重跟踪结果Fig.11 Echo re-tracking result

图12、图13、图14分别展示了回波重跟踪过程中,回波前沿、有效波高、归一化回波幅度的收敛过程,可以看到3项参数均快速收敛。

图12 回波前沿收敛过程Fig.12 Converge procedure of echo front

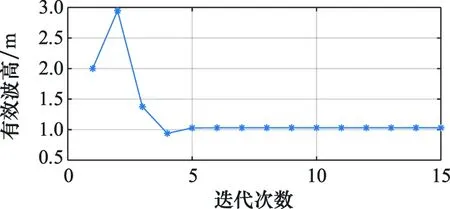
图13 有效波高收敛过程Fig.13 Converge procedure of SWH

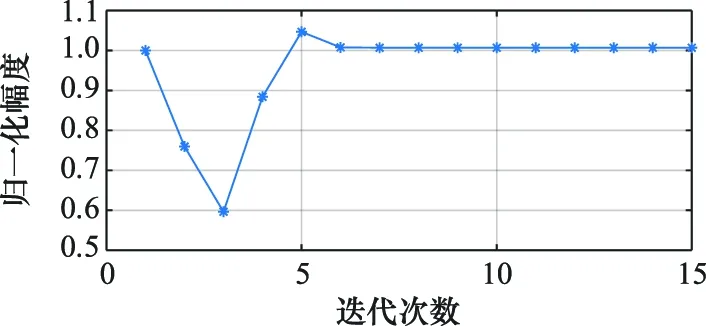
图14 归一化回波幅度收敛过程Fig.14 Converge procedure of normalized echo amplitude

图15是SAR高度计448个多视回波的海表面高度(sea surface height, SSH)反演结果,SSH由回波前沿跟踪结果结合轨道高度、采样起始距离、光速c计算得到:

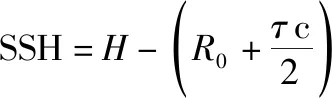
(29)

图15 SSH反演结果Fig.15 Retrieval result of SSH

3.4 SSH反演结果验证

利用丹麦科技大学发布的平均海表面(mean sea surface, MSS)高度模型数据对反演得到的SSH数据进行验证。图16为机载挂飞区域对应的MSS数据。

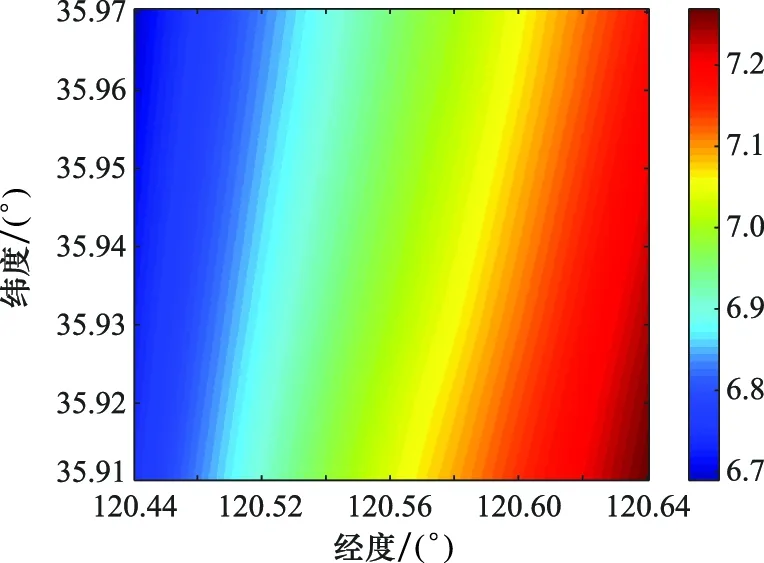
图16 机载挂飞区域对应的MSS数据Fig.16 MSS of airborne flight area

根据挂飞航线的经纬度对MSS数据进行提取,结果如图17所示。

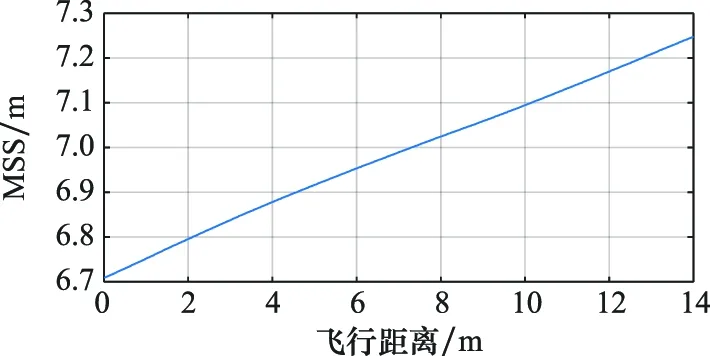
图17 机载挂飞航线MSSFig.17 MSS of airborne flight path

MSS数据由多年的高度计测量结果平均得到,它去除了随时间周期性变化的潮汐的影响;而直接观测到的SSH是瞬时海表面高度,其中含有潮汐分量。不过,由于潮汐的空间尺度很大,因此在机载飞行的14 km内,可以近似认为潮汐是一个固定值。结合以上两点可知,机载数据反演的SSH与MSS模型数据之间存在一个相对固定的偏差。

将SSH反演数据与挂飞航线MSS数据进行对比,如图18所示,两者去除了相对偏差。可以看到,蓝色曲线与红色曲线更加吻合,两者的均方根误差为1.94 cm;而绿色虚线与红色曲线的均方根误差为2.21 cm。以上结果验证了参数反演的正确性和本文回波模型的优势。

图18 SSH与MSS对比结果Fig.18 Comparison result of SSH and MSS

4 结 论

本文首先研究了SAR高度计回波预处理方法,包括多普勒波束锐化、子视回波配准、延迟距离校正和多视处理等;然后研究了改进的回波模型和最小二乘重跟踪算法;最后基于前文形成的全链路数据处理方法,对Ka频段SAR高度计海面机载试验数据进行处理,反演得到了飞行航线对应的SSH。反演结果与模型数据非常吻合,验证了本文数据处理方法的正确性。