基于HTLBO算法的舰载机机群机库维修任务调度

张 勇, 李常久, 苏析超,*, 崔荣伟

(1. 海军航空大学航空作战勤务学院, 山东 烟台 264001; 2. 海军航空大学航空基础学院, 山东 烟台 264001)

0 引 言

舰载机作为航母编队的核心作战单位,在海上战场争夺制空权、空对潜防御、电子对抗和对舰打击等方面发挥着重要作用。维修对舰载机的安全性和可靠性起着至关重要的作用,可显著影响机群持续作战能力,且随着作战或训练强度的提升,维修能力的制约影响显得更为突出。

为提高舰载机机群的出动效率,缩短舰载机的维修保障时间,要求形成高效的维修保障任务规划。但相较于陆基修理厂,航母机库内空间小、环境复杂,对维修人员协同程度要求高，维修人员编制、设施设备等资源受限且对维修时限要求严格,给维修任务调度带来了挑战。基于航母机库的环境特点,科学地对机库内维修人员和设施设备进行调度时序规划和资源分配,缩短作业时间,提高资源的利用率,是提高机库内机群维修效率的关键,这对舰载机机群尽快恢复可用状态并形成战斗力具有重要的意义。

当前,针对航母舰载机维修方面的研究尚处于起步阶段。曾斌等[1]提出了一种考虑定期计划和随机保障时间的综合可用度约束模型,并用启发式求解算法生成了舰载机保障作业调度方案和装备计划性维护时间安排;纪云飞等[2]根据舰载机维修特性中人员、环境、设备等的实际情况,依据业务流程重组理念将舰载机舰面维修工作流程进行了剔除、调整、并行和简化,实现了理论流程向实际工作的流程优化;Feng等[3]利用Multi-agent技术对舰载机综合保障过程进行建模,针对舰载机故障与维修的扰动影响,构建了舰载机作业动态仿真模型,并将其应用于维修人员配置优化。

在与舰载机维修密切相关的装备维修保障任务调度和飞机维修调度领域,国内外学者开展了诸多卓有成效的研究。面向装备维修任务调度领域,昝翔等[4]构建了一种考虑时间不确定的性战时装备维修任务调度模型,以修复装备重要度之和最大为目标,并采用一种改进最大-最小蚂蚁启发式系统求解;曾斌等[5]使用将启发式算法与混合Petri网相结合的求解方式,建立了预留空余停工时间的不确定性调度模型,提高了调度应对突发事件的能力;万明等[6]基于维修效益最大化的目标建立了战时装备维修任务调度模型,设计了两套优化目标不同的调度算法,有效地解决了计算最大保障时间和维修效益、维修负载均衡性的问题。面向飞机维修调度,Safaei等[7]围绕军用机群维修计划案例建立了混合整数数学规划模型,详细描述了维修任务中劳动力的资源约束,并使用经典分支定界的方法求解;Lin等[8]提出了一种受酵母繁殖过程启发的求解算法,以最小化维修完工时间和平衡机库资源数量机群的维护成本为目标,建立基于机群维修决策模型的保障模型;De等[9]使用仿真与优化相结合的模型增强启发式算法求解混合整数线性规划模型,使完工需求时间到达最小且最小化维修人员总劳动力成本。

从以上研究可以看出,在解决此类维修调度问题上,模型抽象方法的研究视角经历了由车辆路径模型[10]、项目调度模型[11]、流水车间模型[12]向资源受限项目调度模型[13]不断深化的过程;模型约束条件由理想化向现实化转变,模型更加精细复杂;模型求解方法经历了由精确式解法[7]向启发式算法[8-9]的转变。

综上,这些研究为舰载机机群机库维修调度提供了理论参考,但在实际应用中仍存在以下几个方面的不足:一是现阶段对于机群机库维修保障任务的优化研究目标大多集中在最小化维修完工时间,尚缺乏对于机群波次出动的可用度需求的考虑;二是维修任务单一,尚未考虑故障维修和定检维护等多模式混合情况;三是对维修保障范围、维修可并行容量、维修工位空间等现实约束考虑不全面。

针对以上不足,本文以舰载机机群机库维修任务调度问题(maintenance task scheduling problem of aircraft in hangar, MTSPAH)为研究对象,针对舰载机波次出动的实际需求,结合维修作业的约束特征构建MTSPAH模型,并设计了混合教与学算法(hybrid teaching-learning-based optimization, HTLBO)用于模型求解,以优化机群的波次可用度和维修资源负载的均衡性。

1 问题描述

舰母机库的机群维护对保障舰载机的安全性和可靠性起着至关重要的作用。航母舰载机在执行飞行任务前后都需要进行故障检测,如检测出重大故障,则会将其回收至机库,入位系留后排队等待维修。除了计划外的随机性故障维修工作,还需完成计划内的预防性定期检查维护,通常包括25 h、50 h、100 h定检维护等。机库需完成广泛的维修任务和定检工作,以保持高水平的机群可用性。机群可用性还取决于机库的维修定检吞吐效率,因此对相关维修人员和设施设备进行科学的时序规划和资源分配是MTSPAH的关键。图1是库兹涅佐夫号航母机库维修资源环境的综合态势,其中涉及的特定约束包括以下4个方面。

1.1 作业流程

针对作业流程的前后序约束关系,可采用节点活动式(activity on node, AON)有向网络图来描述。针对故障维修任务,各维修工序之间为串行关系:故障定位—故障维修—复检;而针对定检维护任务,维修工序之间为网络化的前后序关系,即任意工序的紧前工序集不唯一。图2左侧为多机保障流程网络图,Oij表示待维修机群中的第i架舰载机的第j道工序,OS和OE分别表示虚拟开始和虚拟结束工序,虚拟工序不需要消耗任何保障资源,工期为0,其作用是将所有定检维修流程工序整合在一起。

1.2 维修人员与技能

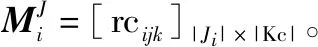
1.3 维修设备/车间

1.4 维修工位空间

针对维修工位空间约束,令rsijk表示维修工序Oij对第k类(k∈Ks)工位的对应关系,rsijk=1表示占用该类工位,否则rsijk=0。舰载机维修中的部分工位,诸如座舱等保障工位，由于空间受限,仅可容纳一定人数nsik进行并行保障作业。

2 模型建立

本节将在模型假设的基础上结合模型的约束条件建立MTSPAH的数学优化模型。

2.1 模型假设

为建立MTSPAH模型,提出如下假设:

(1) 固定类维修资源储备充足,机库内转运时间相对于维修时间可忽略;

(2) 对任意维修工序,具备所需技能的维修人员使用对应技能进行保障;

(3) 不考虑任务变更等突发因素的干扰,维修工序一旦开始不可中断;

(4) 采用一体化联合维修模式,维修人员对同机型各舰载机均可保障。

2.2 模型的变量与约束条件

MTSPAH模型的其余所需变量定义如下:

I:待维修舰载机集合,I={1,2,…,Nm};

pi:第i架舰载机的维修停机位;

Ji:第i架舰载机维修工序集,Ji={1,2,…,|Ji|};

J:机群的维修总工序集,J={(i,j)|i∈I,j∈Ji};

At:机群在t时刻处于执行状态的所有维修工序集;

Ait:第i架舰载机在t时刻处于执行状态的维修工序集;

Psij:工序Oij的紧前工序集合;

Exi:第i架舰载机入位系留完毕时间;

dij:工序Oij的维修作业工时;

Ks:工位空间类别集合,Ks={1,2,…,|Ks|};

nsik:第i架舰载机第k类工位容纳的人员数量;

Smij:维修工序的保障开始时间;

Emij:维修工序Oij的保障结束时间。

决策变量如下:

约束条件包括:

Smi1≥Exi, ∀i∈I

(1)

Smij≥Smi h+di h, ∀(i,h)∈Psij; ∀(i,j)∈J

(2)

Smij+dij≤Smeg+BM·(1-Ypijeg), ∀(i,j),(e,g)∈J

(3)

Smij≤Smeg+BM·(1-Yeijeg), ∀(i,j),(e,g)∈J

(4)

(5)

(6)

(7)

(8)

(9)

(10)

Xpijkl,Xeijk′l′,Ypijeg,Yeijeg∈{0,1},
∀k∈Kc; ∀l∈Lp; ∀k′∈Ke;
∀l′∈Lek′; ∀(i,j),(e,g)∈J

(11)

式(1)表示单机开始维修的入位时序约束;式(2)表示各舰载机的维修工序需按照既定维修流程的前后序依次开展;式(3)表示维修人员冲突的优先序约束,其中BM为足够大实数,确保不等式恒成立;式(4)表示维修设备/车间冲突的优先序约束;式(5)表示任意工序对技能的需求量应与分配至该工序且选择本技能的维修人员数量相匹配;式(6)表示任意工序对各类维修设备/车间的需求与分配至该工序的资源相匹配;式(7)表示每位维修人员对任意维修工序进行维修作业最多使用其中一项技能;式(8)表示供电站等固定类保障设备受供给管路长度的限制;式(9)表示工位空间资源约束;式(10)表示维修车间可并行作业;式(11)表示决策变量Xpijkl、Xeijk′l′、Ypijeg和Yeijeg均为0-1决策变量。

2.3 目标函数

面向舰载机机群机库维修任务需求,分别构建机群波次可用度和维修人员负载均衡性两类优化目标。一般维修任务的目标设置为完成时间最小化,而由于舰载机通常以集中机群发起攻击,这使得舰载机的出动方式多以波次出动为主,最大化出动计划中可用机群数量是前提。在接到舰载机机群出动作战的指令后,若现存功能完好的舰载机数量不足本波次所需数量,即存在维修或定检任务未完成的舰载机，无法进行补充,这将导致该波次出动中机群数量不足。针对波次出动作战需求,本文定义波次可用度表示待维修机群在后续各个出动波次准备时刻的加权可用度,波次可用度越大,表示维修作业为各波次提供的完好舰载机越多,越能满足波次出动数量的要求。其次，是使得维修人员的负载方差最小化,以增加维修作业的可持续性。

(1) 最大化机群波次可用度

(12)

式中:W为出动波次集合;SWw为波次w的出动准备开始时刻;vw表示对波次可用度的倾向权值,越靠前的波次对战局影响越重要,所取权重越大;ETi表示舰载机i的维修完工时间;函数sgn(x)为阶跃函数,当且仅当x≥0时，sgn(x)=1,否则为0;WA定义了机群维修开始后续出动波次的平均可用度,WA的目标是最大化出动波次集合中的加权可用度之和。

(2) 最小化维修人员负载方差

(13)

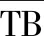
3 HTLBO算法设计

基于以上MTSPAH模型的特点分析,将机库内舰载机机群维修任务调度划分为资源受限项目调度问题(resource constrained project scheduling problem, RCPSP)。由于RCPSP已被证明是一种Np难问题,在可接受的时间内,现有的精确式解法只能解决小规模的问题。在面对大规模调度问题时,使用启发式算法求解引起了人们的关注,并可以高效求得接近最优的解决方案。

通过对RCPSP的深入研究,将经典的RCPSP与实际机库维修调度任务相结合,特别是在维修人员或多功能机器等资源的调度过程中,每种资源掌握几种不同的技能。基于这一特点,将MTSPAH定义为多技能资源受限项目调度问题(multi-skill resource-constrained project scheduling problem, MS-RCPSP)[13]以使其更接近实际机群机库维修情况。MS-RCPSP研究从时间和资源上合理安排调度,在技能与资源最优利用的同时实现既定目标的最优化。

针对上述问题建模,启发式算法可实现优化性能和计算效率的平衡[13-15],可借鉴成果较为丰富。与粒子群优化(particle swarm optimization, PSO)算法、遗传算法(genetic algorithm, GA)和差分进化(differential evolution, DE)算法等类似,教与学优化(teaching-learning-based optimization, TLBO)算法也是一种基于种群的启发式算法,它提供了一个模仿课堂上教师与学生教学过程的优化模型,优化过程包含教师的教学阶段和学生们的互相学习阶段[16-18],来实现全局最优结果的求解。TLBO算法与其他算法的不同之处在于其不需要任何特定于算法的参数设定[18],避免了因参数的设定不同而导致算法的优化效果不同。该算法在流水车间调度[19]、作业车间调度[20]、炼钢-连铸调度[21]等问题上均有较成功的应用,具备良好的优化性能和问题适应性。

本文在标准TLBO算法[18]的基础上,针对MTSPAH模型的特点,设计了一种HTLBO算法,算法流程如图3所示。

算法具体的执行步骤如下:

步骤 1初始化阶段。首先根据机群机库维修任务,随机初始化规模为Np的种群,并基于解码策略求解种群对应适应度值;进而择优选择规模为Nt的精英教师群体,令迭代次数G=1。

步骤 2教师教学阶段。随机从精英教师群体中选取任意教师,选取任意学生个体采用面向精英教师的DE变异策略进行个体更新,随后将新个体与原个体进行二项交叉,并基于贪婪选择更新学生和精英教师群体。

步骤 3学生学习阶段。对任意学生个体,从剩余学生群体中随机挑选学习对象,采用峰值交叉[22]机制互相学习,并基于贪婪选择更新学生和精英教师群体。

步骤 4强化学习阶段。从精英教师群体中随机抽取教师个体,执行学习自动机的自适应邻域搜索(learning automata-adaptive neighborhood search, LA-AVNS)操作。

步骤 5令G=G+1,判断是否达到迭代终止条件,若是,则迭代终止,并输出最优教师个体对应的维修调度方案和资源分配方案;否则,转入步骤2继续教与学优化迭代。

HTLBO的主要改进点体现在以下3个方面:

(1) 在教师教学阶段,引入基于精英种群的DE算子进行种群的更新;

(2) 在学生学习阶段,引入峰值交叉算子进行种群个体间的交叉学习;

(3) 在强化学习阶段,引入LA-AVNS操作对精英种群进行局部增强搜索。

3.1 编码操作

编码策略是影响算法搜索效果和效率的重要因素。求解RCPSP问题的主要编码策略包括任务列表编码、优先数编码和优先规则编码[23]。由于调度过程中工序之间的优先级关系,采用任务列表和优先规则的编码形式可能在后续的交叉和变异中获得不符合实际调度规则的工序组合,因此采用基于维修作业时序修正的优先数编码,即x=[S11,S12,…,S1|J1|,S21,…,SNm|JNm|],以避免在后续的操作中产生非法的子代。

3.2 解码操作

解码机制包括串行调度生成机制(serial scheduling generation scheme, SSGS)和并行调度生成机制(parallel scheduling generation scheme, PSGS)两类[24]。文献[25]研究表明PSGS相比SSGS在更小的解空间中搜索结果,在大种群及资源受限的情况下,PSGS的解空间可能不包含最优解。因此,对于机群机库维修调度这种非常规性能指标计算的条件,选择SSGS生成维修作业时序方案具有搜索效果和效率的优越性。与常规SSGS不同,HTLBO针对任一待调度工序Oij,在可满足各类约束的时序推进搜索过程中,嵌入任务技能对维修人员的匹配满足性进行判断,即在时序调度过程中同步进行维修人员的分配和技能的选择。考虑到多技能维修人员的柔性更大,在对维修人员进行分配时,优先选择技能数较少的维修人员进行分配,确保后续维修工序有更多柔性维修人员可分配;在同等技能数条件下,则优先选择累计维修时间最少的维修人员,以增强维修人员的负载均衡性;在维修设备分配方面,采用基于覆盖范围内剩余工序作业时间最少优先规则;在维修车间分配方面,依照尽量集中资源的原则,将维修人员分配至当前作业数最多的车间。

定义已完成调度工序集Sg,可调度工序集Dg,解码调度过程是从Dg中按工序优先级选取工序,并安排在最早可开工时刻,分配人员、设备资源,并加入集合Sg这一循环迭代过程。解码调度执行流程图如图4所示。

3.3 适应度函数

为便于算法进行个体适应度比较,将字典序分层目标通过赋予权重组合为单目标,并定义个体适应度为

f=(1-WA)+αLBM

(14)

式中:α(0<α≪1)为维修人员负载方差的权重系数,维修调度指挥员可根据保障需求进行权重调节,鉴于舰载机机群机库维修任务的需求为优先保证提供完好的满足波次需求数量的舰载机,故可将权重系数取为小量。

3.4 教师教学阶段

这一阶段利用精英个体(教师)来引导种群个体(学生)的学习以提升整个班级的水平。对此,面向精英的DE操作具备更好的引导作用。在标准DE算法中,面向精英的变异机制一般以最优解作为引导,为模仿教师教学过程,并增强教学阶段的多样性,借鉴文献[26]中“DE/target-to-best/1”策略,提出面向精英教师群体的教学引导机制:

(15)

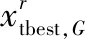
3.5 学生学习阶段

这一阶段学生通过相互学习来提升各自的水平,同时可增加班级群体的学生多样性以避免陷入教师教学阶段可能出现的局部极值。对此,采用GA中的峰值交叉[22]来实现学生间的相互学习作用。在峰值交叉中,采用资源利用率作为引导因子,资源利用率较高的峰值区间往往隐藏着作业的瓶颈,以此时段作为交叉区间,从而实现个体之间的优势互补。

首先,给定维修方案S,t时刻的瞬时资源利用率(Instantaneous resource utilization rate, IRUR)定义为

(16)

(17)

进一步地,基于TIRU定义,综合资源利用率最高的峰值区间可表示为[tp1(S),tp2(S)],且长度为l的峰值区间起始时刻可由下式计算得出:

(18)

鉴于峰值区间包含了个体的优良基因,算法采用两点交叉进行峰值区间的优先数编码置换。

3.6 强化学习阶段

本阶段是在经典TLBO算法的基础上引入的新阶段,目的是对优秀教师个体做进一步的强化学习,以更好地引导班级群体的学习更新。对此,基于LA-AVNS框架,结合本问题特性,设计相应的搜索邻域如下:

(1) 交换邻域

随机选取两个无紧前紧后约束的维修工序,交换其编码优先数。

(2) 维修故障工序前插邻域

随机选取一个维修故障工序,查询其紧前工序的结束时间并将其作为可插入区间的起始值,本工序开始时间为区间终止,将该工序插入区间内的任意位置。该邻域主要可使得故障舰载机尽快实现维修。

4 维修案例仿真分析

4.1 维修案例的构建

维修案例基于图1所示的航母机库环境,考虑故障维修和定检维护等多模式混合情况，设置10架编号分别为A～J的舰载机进行机库维修定检:其中6架故障舰载机为波次回收后由甲板转运至机库,4架机库驻留舰载机执行定检维护。后续的出动波次包括3次,且波次间隔周期为1 h 40min,即SW=[100,200,300]min,波次权重设置为v=[0.5,0.3,0.2]。

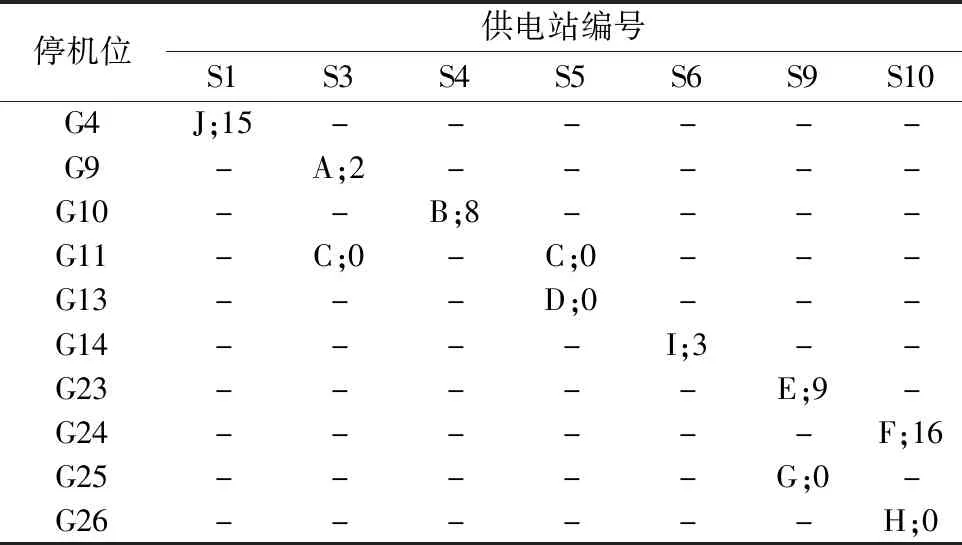
表1 案例任务设置机库供电站与机群停机位覆盖关系 Table 1 Case task hangar power station and fleet parking space covering relations min

针对同型号舰载机,构建定检的通用化单机定检流程AON有向网络图如图5所示,虚线代表与虚拟工序连接。

各定检保障工序工时、资源和技能需求如表2和表3所示。本案例中特设、航电、军械和机械的维修人员配置数量为[5,6,4,10],专业技能兼容设置为特设与航电兼容,军械和机械兼容,各专业内前4名维修人员具备相应兼容专业技能。

表2 单机定检保障工序工时需求 Table 2 Regular maintenance operation hours demand of single aircraft min

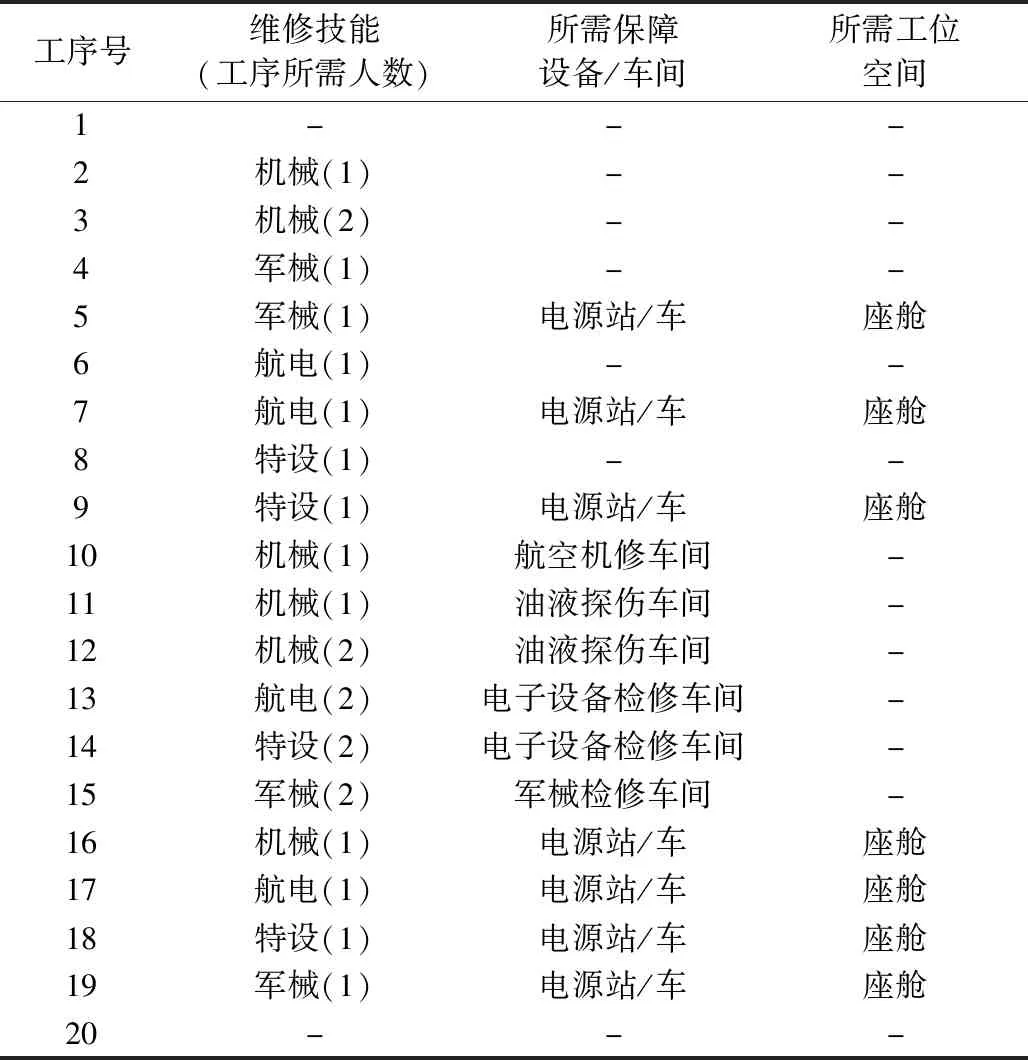
表3 单机定检保障工序技能资源需求Table 3 Regular maintenance operation set and resource demand of single aircraft

在维修车间配置方面,受机库周边舱室空间所限,航空机修车间、电子设备检修车间、军械检修车间、油液探伤车间各配置一间,且可并行作业工序数为Ne=[3,2,4,1]。工位空间约束考虑座舱空间,且可并行作业人数为1人。

4.2 算法仿真对比分析

为验证本文提出的HTLBO算法的有效性以及求解MTSPAH的性能,选取TLBO算法、DE算法和PSO算法作为求解此问题的性能对比算法。各算法的参数设置如下:HTLBO中班级学生规模Np=30,精英教师群体规模Nt=5,交叉概率cr=0.1,变异概率F=0.1;TLBO中Np和Nt的设置同HTLBO算法;PSO算法中粒子数量N=30,学习因子c1=2,c2=2,选用线性递减权值策略设置ω=(ωini-ωend)(Q-q)/Q+ωend,其中ω为可变惯性权值,Q为最大评价次数,q为当前评价次数,初始权值ωini=1.2,迭代结束权值ωend=0.1;DE算法中种群规模为Np=30,交叉概率cr=0.1,变异概率F=0.1。以上算法适应度函数中维修人员负载方差的权重系数α=10-6,且均以评价次数Q=5 000作为迭代结束的标志。经过仿真优化,得到MTSPAH的优化指标波次可用度WA与维修人员负载方差LBM的对比变化趋势如图6和图7所示,各算法独立运行15次得到的统计数据如表4所示,评级标准选取最优解(Bes.)、平均解(Avg.)和标准差(Std.)。

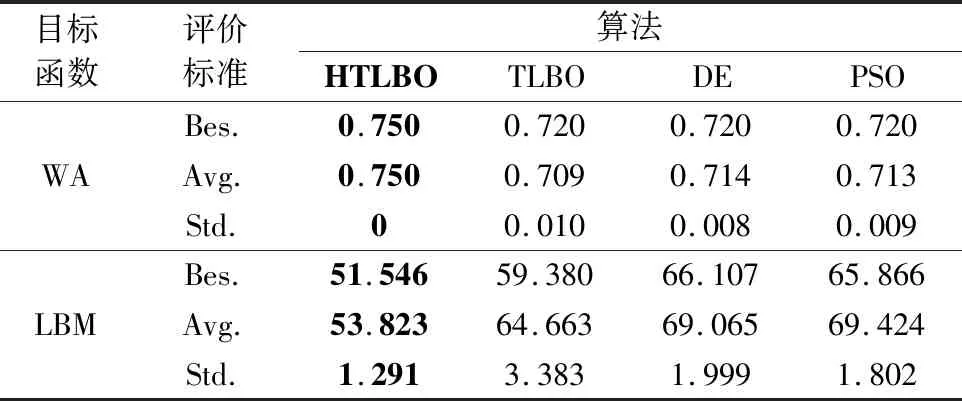
表4 算法结果统计数据 Table 4 Algorithm result statistics

通过仿真的对比结果可以发现,本文提出的HTLBO算法在求解MTSPAH相较于对比算法具有寻优能力强、收敛速度快、结果波动小的特点,其原因有如下3点:教师阶段引入的DE算子寻优能力和寻优速度优于其他3种算法;学生学习阶段引入的峰值交叉算子,实现了高资源利用率个体交叉向后代传输在调度中的理想特征;强化学习阶段引入的LA-AVNS框架对种群进行局部增强搜索操作,提高了最优解的精度和稳定性。

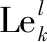
为验证算法在大规模机群维修资源高度受限条件下,算法的优化求解性能,将出动波次间隔时间更改为80 min,进行算法压力测试仿真,设置3组出动任务如表5所示,其他算法参数保持不变,各算法独立运行15次得到统计数据如表6所示。

表5 机群保障任务 Table 5 Aircraft group support tasks

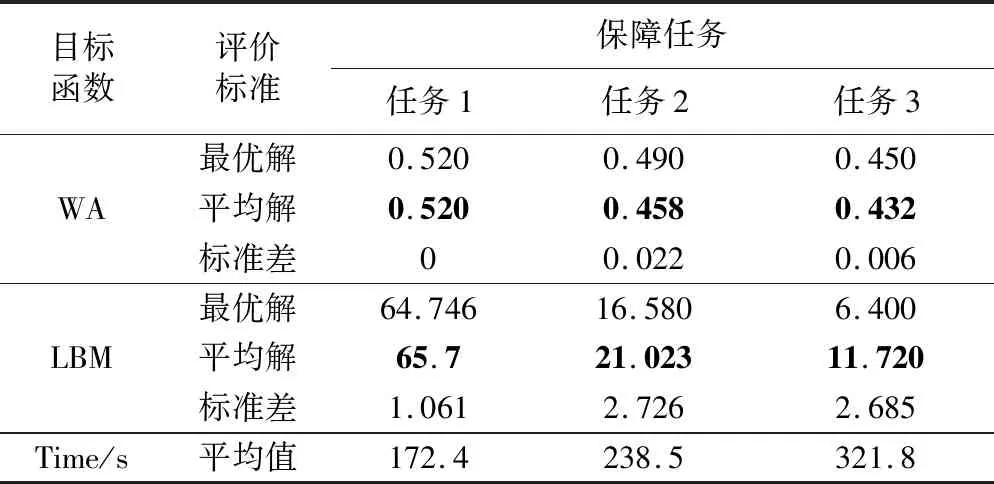
表6 高强度任务仿真结果统计数据 Table 6 Simulation results of high-intensity tasks

通过仿真的对比结果可以发现,在波次间隔时间缩短后,随着机群数量的增加,机群波次可用度WA逐渐降低,维修人员负载方差LBM逐渐降低。经分析，其原因是在维修任务紧张、资源高度受限情况下,波次间隔时间内提供足够舰载机的比率逐步下降,同时由于维修人员维修任务的大量填充,任务空闲时间间隔被压缩,致使维修人员间的维修工作时间差距变小,负载方差变小,所得结果分析符合预期。同时可以看出，算法求解调度任务计算时间(Time)逐渐增加,但仍在可接受的求解时间范围内。综合上述,本文提出的HTLBO算法在求解高度资源受限下的MTSPAH时仍具有较好的性能表现。

5 结 论

本文针对航母舰载机机库维修任务调度问题,以舰载机机群波次可用度和机库维修人员负载均衡性为优化指标,提出了一种HTLBO算法。经过案例仿真和对比实验,初步证明算法在解决这类问题上有一定的优势,并给出了一种最优维修人员调度方案。但本文模型和算法的研究目前仍具有局限性,其不考虑任务变更等突发因素的干扰且维修工序一旦开始不可中断的前提假设与实际复杂的维修环境不符,后续的研究将继续改进算法以实现动态调度，来更加贴近实际机群机库维修调度。