水文地质试验在隧道工程地质勘察中的应用及涌水量预测

程小勇

(广东省交通规划设计研究院集团股份有限公司，广州 510507)

隧道是公路交通工程中的重要构筑物，特别是深埋特长隧道往往是关键控制性工程，其中水文地质勘察及涌水量的预测是隧道施工设计方案的重要组成部分，但因水文地质条件的复杂性及涌水理论和公式参数的制约，通常很难精准判断隧道涌水位置并准确预测涌水量。为此，需在水文地质试验工作基础上，采用合理的水文地质概念模型和水文分析方法，最大限度地评估隧址区是否存在富水段落，并估算不同水文地质条件下隧道洞身的涌水量，提前做好隧道涌水的预防措施[1-7]。

现场钻孔抽水试验和压水试验是获取隧道岩体渗透系数的主要方式。钻孔抽水试验是通过钻孔抽水，采用抽水量与水位降深值的函数关系式来计算含水层渗透系数的一种原位渗透试验。钻孔压水试验是按照某一指定深度将钻孔分隔成若干钻孔段，用不同的压力对各试验段进行压水并测定其相应的流量，由此得到岩体透水率渗透系数，是根据压力和流量的关系来确定岩体渗透系数的一种原位渗透试验[8-11]。

根据抽水试验、压水试验获取的岩土体渗透系数，并结合其他综合勘察成果，对隧道涌水量进行预测。一般常选用降水入渗系数法、裘布依理论式及古德曼经验式。有学者根据已建成通车的特长隧道在开挖过程中发生的涌水情况进行分析研究[12-14]，认为深埋特长隧道在淋水状出水时，多数为张性节理裂隙带的富水所致，可采用降水入渗系数法、裘布依理论式进行预测正常涌水量；遇到高压股状出水时，视为较大规模断裂构造带导水所致，可采用古德曼经验式进行预测最大涌水量[3,14]。

本文依托拟建的深圳外环高速三期田头山隧道工程，结合勘察钻孔进行孔内抽水试验、水位恢复试验、压水试验，采用降水入渗系数法、裘布依理论式及古德曼经验式对隧道涌水量进行预测、分析及评价。

1 田头山隧道地质特征

1.1 工程概况

拟建田头山隧道是深圳外环高速三期关键控制性工程，为分离式隧道，里程桩号为K82+660～K87+712，单洞长5 052 m，进口标高约61.9 m，出口标高约68.5 m，纵坡采用人字坡，最大埋深约430 m，为深埋特长隧道。隧址区位于剥蚀低山地貌区，线路轴线处最高标高在K84+460，高约498 m，最低标高在隧道出口附近，约69 m，相对高差约429 m。隧道走向与山脊走向近垂直，隧址区山体地形坡度总体上陡下缓，下部自然坡度一般30°～40°，中上部自然坡度一般50°～60°，局部为岩质陡坎，山体植被发育。

1.2 工程地质

隧道K82+660～K85+000段，为泥盆系上统双头群粉砂岩及其风化层；K85+000～K86+000段，为泥盆系中统鼎湖山群粉砂岩；K86+000～K87+500段，主要为侏罗系下统桥源组泥质粉砂岩；K87+500出口段，主要为侏罗系下统金鸡组泥质粉砂岩。

隧道经过山体为一复式褶皱发育构造，背斜位于隧道中部K85+000～K85+500附近，向斜位于K86+050～K86+400附近。背斜核部为泥盆系(D)砂岩，向斜核部为侏罗系(J)砂岩。褶皱轴向近似为东西向，垂直于隧道轴线方向。整个褶皱受到松坑-惠东北西向构造带影响，局部被石英破碎带所切割，核部近似平行于北东向莲花山断裂，受到复杂多期地质构造作用，局部褶皱发生倒转倾倒，微褶皱也很发育，构造活动强烈，对隧道围岩的稳定有影响，也促成了蓄水构造。隧道纵向地质概况如图1所示。

图1 隧道纵剖面Fig.1 Longitudinal profile of tunnel

1.3 水文地质

隧道地下水分为松散层孔隙潜水及基岩裂隙水，水量大小受岩体孔隙率、裂隙发育程度及季节变化影响，补给来源主要为大气降水下渗补给。

1) 松散层孔隙潜水：分布于隧道洞身段上部斜坡、脊岭地带，赋存于第四系残坡积粘土层孔隙中，含水层分布不连续，厚度不大，处于斜坡地带，贮水条件较差，仅季节性有水。对隧道工程施工影响小。

2) 基岩裂隙岩溶水：主要赋存于强中风化粉砂岩节理裂隙中，其富水性受大气降水补给动态变化，在构造破碎带及地层接触带富水性强，呈不均匀状分布。由于洞身以上无地表水体，地下水主要接受大气降水补给，隧道区地形较陡，地表径流途径短，流速快，入渗补给地下水总体较弱。基岩裂隙岩溶水为隧道区地下水主要类型，可能产生突水、突泥等现象。

3) 补、排条件及动态特征：区内地下水主要接受大气降水垂直入渗补给；基岩裂隙水赋存于岩体裂隙中，主要受地形地貌控制，通过导水的裂隙系统补给深部含水层或向坡脚沟谷排泄。由于隧道区地形坡度较陡，地表径流排泄条件好，其天然排泄主要为呈线状、散点状排泄于地形切割较深的冲沟、地貌突变处。

2 水文地质试验

2.1 抽水试验

隧道钻孔CSZK2位于隧道中前部K83+768垭口附近，孔深208.60 m，钻探岩芯上部孔段较破碎，裂隙发育，岩性为中风化粉砂岩，具强富水条件，在此孔中开展抽水试验具有代表性。

试验过程中，流量和水位相对稳定，并有一定延续性，根据裘布依井流理论，采用稳定流完整井来计算隧道岩体的渗透系数，计算公式如下：

(1)

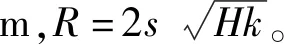
在隧道钻孔CSZK2开展抽水试验，水位的降深次数进行3次，水位降深的最大值接近过滤器长度的1/2深度处，其余2次水位降深值，分别为最大降深值的1/3和2/3。抽水试验时，动水位和出水量观测的时间，在抽水开始后的第5 min、10 min、15 min、20 min、25 min、30 min各测1次，以后每隔30 min测1次。本次抽水试验过滤器下放最大深度为120 m，水位最大降深为63 m，抽水试验结果见表1。由公式(1)计算出隧道钻孔CSZK2试验段岩体的渗透系数K=0.012 4 m/d。

隧道钻孔CSZK2岩芯显示，中上部岩体破碎(距孔口100 m左右)，为富水岩体。钻孔下部岩体为微风化粉砂岩，岩体完整，可成为良好的隔水岩体，只有在断层或其他导水通道联通上部富水岩体与隧道时，才可能发生隧道涌水。

2.2 水位恢复试验

在隧道钻孔CSZK2中开展水位恢复试验，根据不同时刻水位恢复与时间的关系，按下式计算渗透系数。

(2)

式中：s1、s2为不同时刻水位距孔口距离，m；rw为钻孔半径，cm；t为水位恢复时间，s。

水位恢复试验待隧道钻孔CSZK2抽水试验停止后，孔的水位恢复按第1 min、2 min、3 min、4 min、6 min、8 min、10 min、15 min、20 min、25 min、30 min、40 min、50 min、60 min、80 min、100 min、120 min进行观测，以后每隔30 min观测1次，在连续4 h内水位变化不超过1 cm/h，停止观测。水位恢复试验结果见表2。由公式(2)计算出岩体的渗透系数K=0.010 m/d，与抽水试验结果基本吻合。

2.3 压水试验

当试验段位于地下水位以下，透水率q<10 Lu时，可根据不同阶段的压力计算岩体渗透系数。P～Q曲线类型一般为层流或紊流型。

当P～Q曲线为A型(层流)时，用第3阶段的压力值P3和流量值Q3计算岩体渗透系数。计算公式如下：

(3)

当P～Q曲线为B型(紊流)时，用第1阶段的压力值P1和流量值Q1计算岩体渗透系数。计算公式如下：

(4)

式中：Q1、Q3为第1阶段、第3阶段压入流量，m3/d；Hy为试验水头，m；Ly为试段长度，m；r0为钻孔半径，m。

隧道钻孔CSZK4，孔深370 m，为隧道区最深钻孔，位于隧道中部K86+233，地质构造上位于向斜核部，在此钻孔中开展压水试验具有典型代表性。压水试验位置依据钻探岩芯选择在中风化、破碎带、微风化典型深度开展，压水试验采用三级压力、5个阶段，即P1-P2-P3-P2-P1，P1、P2、P3三级压力分别为0.3 MPa、0.6 MPa和1 MPa。在CSZK4钻孔中压水对应不同深度的P～Q曲线类型如图2所示，压水试验结果见表3。由公式(3)、公式(4)计算出中风化、微风化带中岩体的渗透系数分别为0.017 2 m/d和0.006 3 m/d～0.008 1 m/d，公式(3)计算出破碎带的渗透系数为0.765 0 m/d。

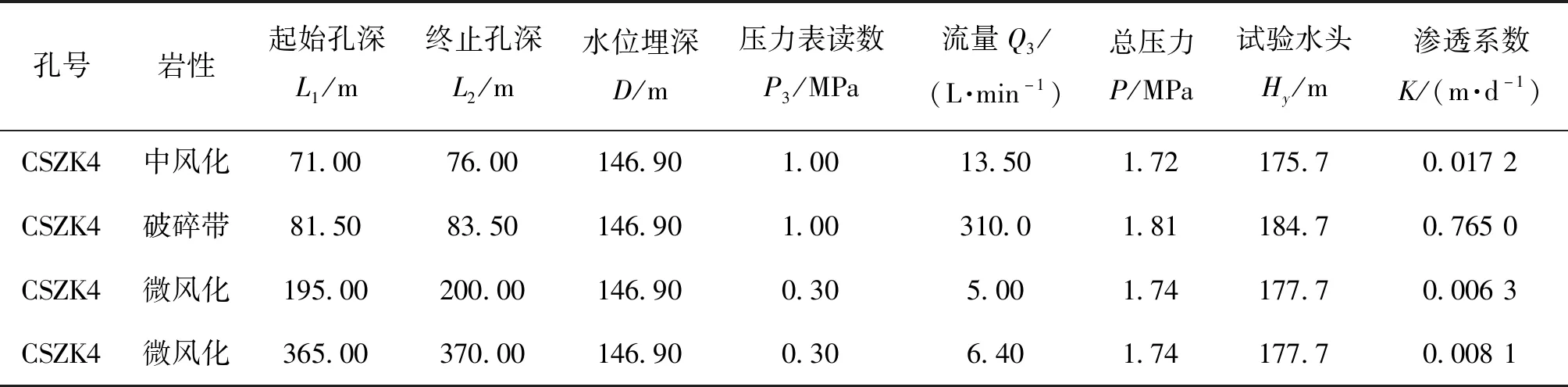
表3 CSZK4中压水试验结果Table 3 Results of pressure water tests in CSZK4

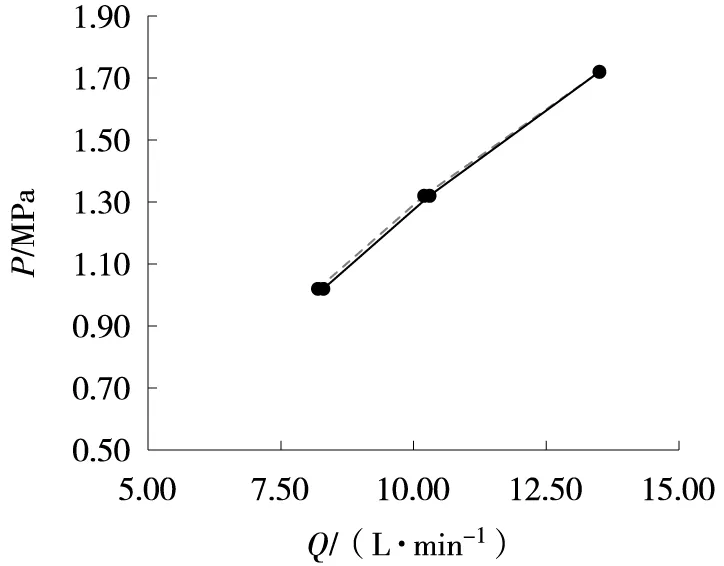
(a) 71.00 m～76.00 m段层流

3 隧道涌水量评价

3.1 降水入渗法

降水入渗法是一种典型的水均衡法，其关键是确定降水入渗系数及集水面积。降水入渗系数作为降水补给地下水的数量指标，是降水入渗补给量与降水量之比，是地下水资源估算与大气水、地表水、地下水三者间相互转化研究中的重要水文参数，其大小取决于地表土层和包气带的岩性、结构、地形、地貌特征，降水量大小及强度、时间分配以及地下水埋藏深度等因素，是一个较难准确测定的参数[15]。根据降水入渗法计算隧道涌水量，计算公式如下：

Q双=2.74αWA

(5)

式中：Q双为双洞正常涌水量，m3/d；α为降水入渗系数，根据隧道综合地质特征情况，暂取0.25 m/d；W为年降水量，mm；A为隧道通过含水体的地下集水面积，km2。

根据隧址区地形及隧道范围含水体地下集水面积范围划分原则，以山顶、山脊作为分水岭或大致与隧道平行且低于隧底的山谷为界，年降水量采用当地多年年均降水量，计算的隧道涌水量见表4。采用降水入渗法公式(5)计算得出隧道单洞正常涌水量约4 295 m3/d。

表4 降水入渗法预估隧道正常涌水量结果Table 4 Prediction results of tunnel normal water inflow by precipitation infiltration method

3.2 裘布依理论式

裘布依理论式是地下水流向井内的平面流稳定运动公式，是法国水力学家裘布依(Jules Dupuit，1 804～1 866)在达西定律的基础上推导而出，它的假定条件为：1) 含水层是均质、各向同性、等厚、水平的；2) 地下水为层流，符合达西定律，地下水运动处于稳定状态；3) 静水位是水平的，抽水井具有圆柱形定水头补给边界；4) 对于承压水，顶底板是完全隔水的，对于潜水，井边水力坡度不大于1/4，底板完全隔水[9]。选用的公式如下：

(6)

根据水文地质试验获取得隧道围岩岩体渗透性系数，结合隧道围岩特征，合理确定不同级别围岩岩体的渗透系数，对隧道进行分段预测涌水量，计算结果见表5。由表5可知，根据裘布依理论式(6)估算隧道左线正常涌水量为9 795 m3/d，隧道右线正常涌水量为9 943 m3/d。

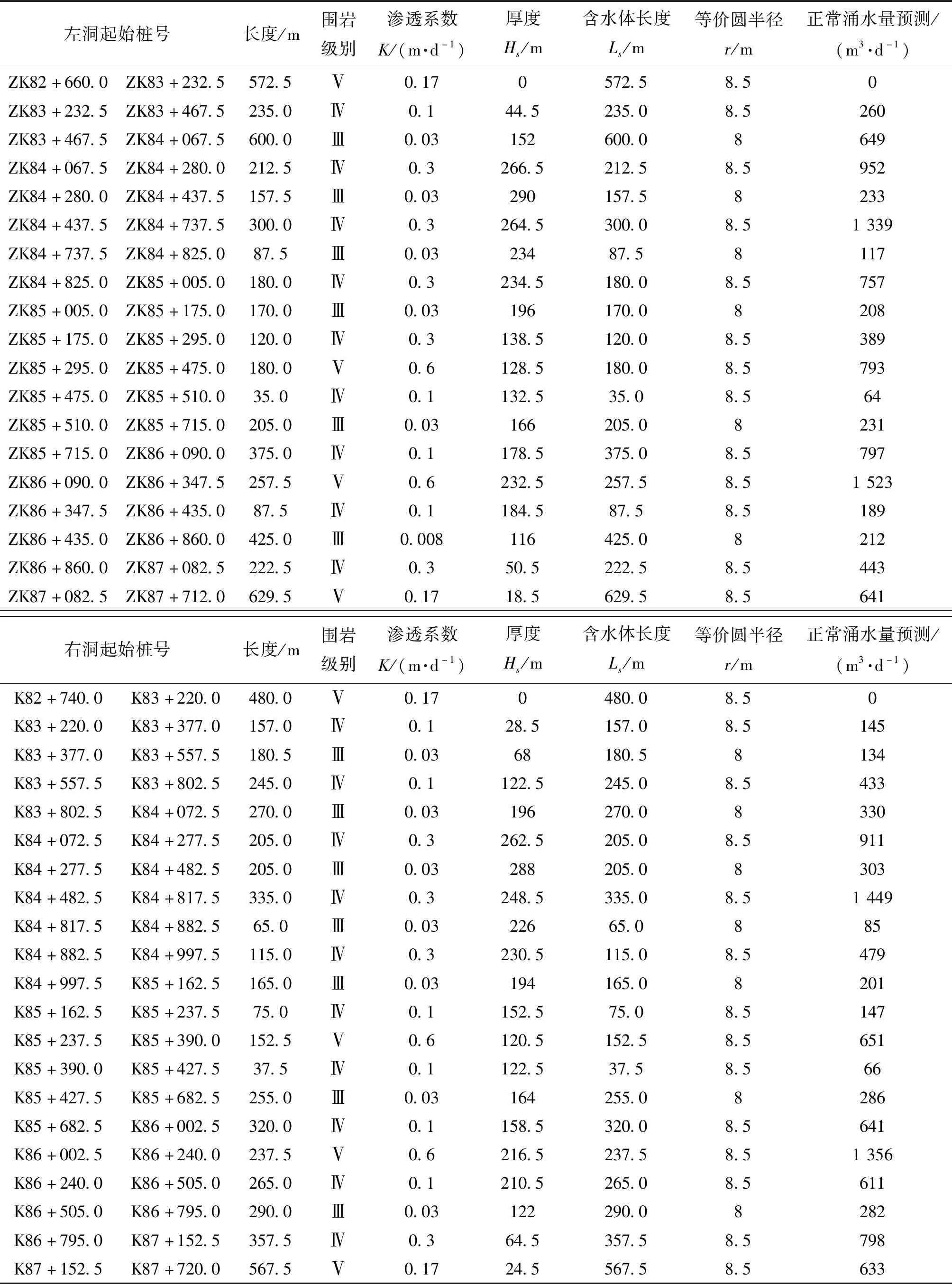
表5 裘布依理论式预估隧道正常涌水量结果Table 5 Prediction results of tunnel normal water inflow by Jubey theory

3.3 古德曼经验式

古德曼经验式是以地下水动力学理论为基础，对地质模型进行了较大程度的简化，遇到高压股状出水时，视为较大规模断裂构造带导水所致，可采用古德曼经验式进行预测最大涌水量[3，14]，计算公式如下：

(7)

式中：Q0为隧道通过含水体地段的最大涌水量，m3/d；H0为静止水位至洞身横断面等价圆中心的距离，m；d为洞身横断面等价圆直径，m。

结合隧道围岩特征，采用古德曼经验式分段预测最大涌水量，计算结果见表6；并由式(7)估算隧道左线最大涌水量为211 163 m3/d，隧道右线最大涌水量为201 522 m3/d。古德曼经验式预测涌水量时，重点突出了较大规模断裂构造带导水通道形成后出现的最大涌水量，是一种上限值，其涌水预测往往高于裘布依理论式和降水入渗法一个数量级，这也在大丰华高速公路鸿图特长隧道中得到佐证，在遇到大规模导水通道高压涌水时，古德曼经验式预测的最大水量与实际出水量较为吻合[14]。

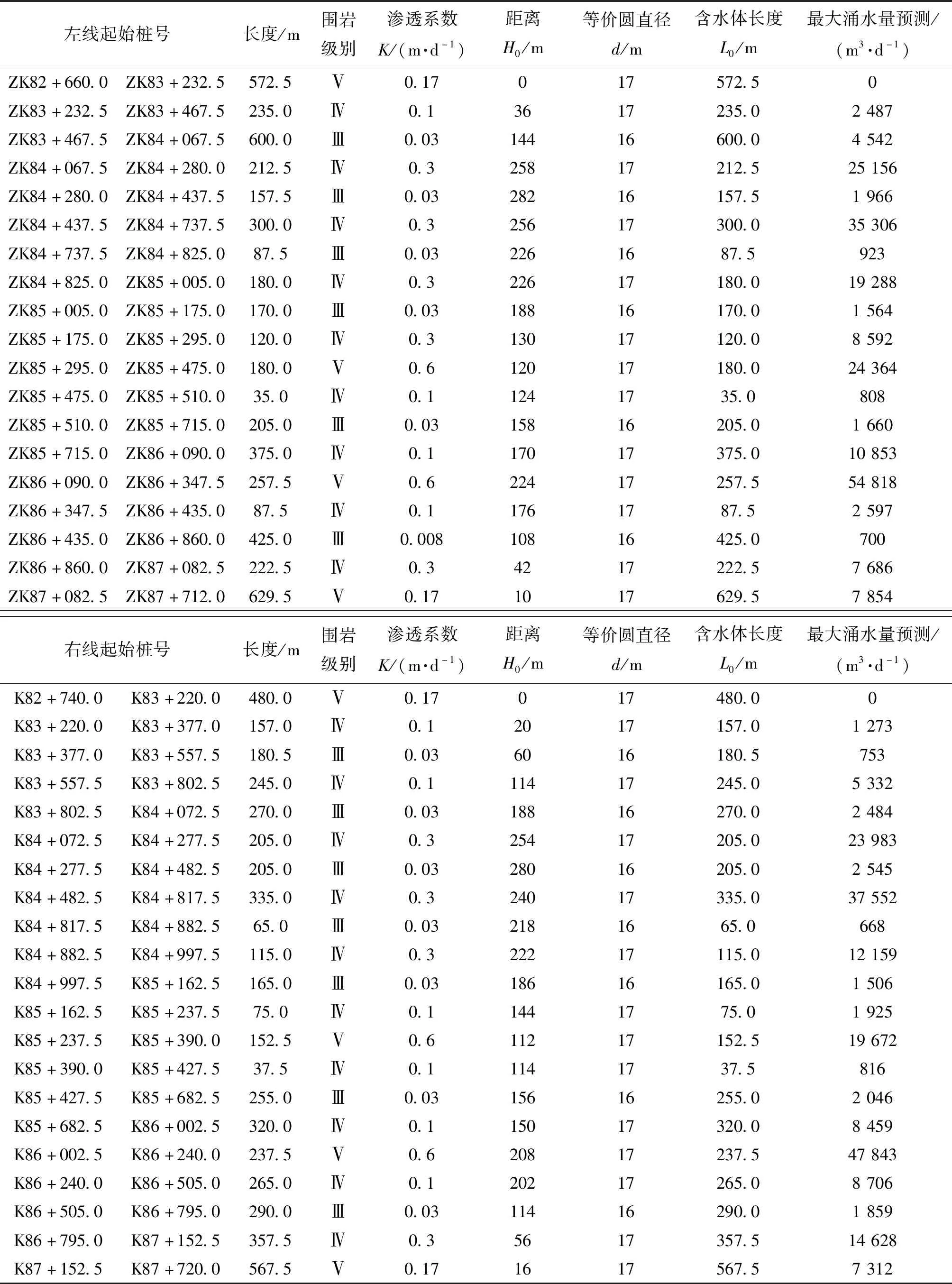
表6 古德曼经验式预估隧道最大涌水量结果Table 6 Results of prediction of maximum tunnel water inflow by Goodman Empirical Model

4 结束语

1) 田头山隧道深埋段围岩多为微风化粉砂岩，完整性较好，为相对隔水层，根据现场水文地质试验结果，认为地下水对隧道施工影响将不会太大，但实际由于受节理裂隙发育带、褶皱构造、强烈风化的影响，局部路段形成导水通道，在隧道施工时可能产生涌水；同时向斜轴部常是地下水富集之处，成为良好的储水构造，开挖后会造成大量地下水涌出，必须注意岩层的坍落、漏水及涌水问题。

2) 采用降水入渗法计算得出隧道单洞正常涌水量约为4 295 m3/d；采用裘布依理论式估算隧道左线正常涌水量为9 795 m3/d，隧道右线正常涌水量为9 943 m3/d；采用古德曼经验式估算隧道左线最大涌水量为211 163 m3/d，隧道右线最大涌水量为201 522 m3/d。这是在极端情况下，大规模断裂构造带导水通道形成后，涌水量的上限值。

3) 由于复式向斜蓄水构造的存在，应密切注意隧道开挖过程中的水文地质问题。隧洞开挖时，洞壁将会有基岩裂隙水渗出，呈滴水或渗流状，特别接近富水段落边缘时，建议采用TSP、地质雷达、超前钻探等手段，及时开展超前地质预报工作。遇到导水通道发生涌水时，应遵照“排堵结合，限量排放”的原则，建议对导水通道进行超前注浆措施，避免疏干方式的排水对隧址区环境造成不利影响。