充填砂颗粒级配对土工织物覆砂渗透特性的影响
2022-07-27满晓磊鲍永健吴海民刘广英
满晓磊,鲍永健,吴海民,刘广英
(1.滁州学院土木与建筑工程学院,安徽 滁州 239000;2.河海大学水利水电学院,南京 210098)
0 引 言
充填管袋技术始于20世纪50年代,最先被应用于国外的海岸防护工程中[1-3];自1985年被引入我国后,凭借其优点在我国河口蓄淡水库、深水航道整治、近海交通设施、内河整治等多种基础设施的建设中得到了广泛应用[4-6]。但目前充填管袋坝的渗流机制尚不明确,渗透模型也未能建立,因此,充填管袋坝的渗流计算与分析至今无法进行,极大地限制了新建坝体的结构设计与已建坝体的安全评价。
揭示充填管袋坝渗流机制的首要任务是探究单个管袋的渗流特性。由于单个管袋是由充填砂和袋体材料共同组成的非均质结构,其渗透性能受到充填砂和袋体材料的共同影响。目前,对于管袋材料与充填料各自的渗透特性研究已比较充分。
考虑到充填管袋在施工及运行期土工织物应力状态的差别,国内外学者对不同应力条件下土工织物的渗透系数进行了研究。Wu 等[7]对土工织物沿纬向施加单向拉力后进行透水试验和梯度比试验,试验结果表明土工织物在受到单向拉伸时等效孔径孔隙会增大,渗透系数随之增大;Fourie 等[8]对不同厚度的土工织物进行了单向拉伸和双向拉伸试验,试验结果表明无论是单轴还是双轴拉伸作用下,土工织物的等效孔径均会随拉力的变化而变化。较厚织物的等效孔径随着拉力的增加而减小,而对于较薄的土工织物,其等效孔径随着拉力的增大而增大,说明拉力对土工织物渗透系数的影响不可忽略;陈轮等[9]通过室内试验研究了拉应变对土工织物的渗透特性的影响,试验结果表明拉应变会使土工织物发生淤堵,且淤堵程度随拉应变的增大而加重,进而降低土工织物的渗透性能。白建颖等[10]在总结国内外关于土工织物渗透性能研究的基础上,通过定性分析,总结了土工织物的微观结构及其渗透原理,并通过定量分析,建立了水头差与渗流流速的经验关系式。
对于纯砂土料渗透系数的研究,国内外学者以常水头试验为主研究了渗透系数的影响因素,并对渗透系数的计算公式进行定量总结、分析。国外,继H.Darcy 之后,众多学者陆续提出了渗透系数k的计算公式,如:太沙基等[11]认为土体的渗透系数k与d102e2成正5 比(e为孔隙比);哈增等[12]通过试验数据分析得出土体渗透系数k与d102成正比;柯森等[13]认为渗透系数k仅与土料孔隙比和d9有关。国内,刘杰等[14]通过试验发现无黏性土的渗透系数与孔隙率n与d20间存在较好的相关关系;朱崇辉等[15]指出粗粒土的渗透系数与不均匀系数和曲率系数存在较大的相关性,用修正的太沙基公式建立了粗粒土渗透系数与级配特征的关系;苏立君等[16]研究了同一粒径级砂土渗透系数随孔隙率的变化和同一孔隙率下不同粒径级砂土渗透系数随均值粒径的变化规律,并最终拟合出渗透系数的经验公式;杨兵等[17]采用常水头试验方法,研究了砂土不均匀系数、曲率系数、平均粒径对渗透系数的影响,结果表明渗透系数随曲率系数增大而增大,随不均匀系数的增大而减小,且与平均粒径的变化关系接近线性正相关。
对于管袋材料与充填料组成的系统的渗透特性,国内学者也进行了初步探究。吴纲等[18]采用自主研制的一套多功能渗透试验装置,开展了一系列纯土和有纺土工织物覆土条件下的渗透试验,结果表明:有纺土工织物对于土体渗流略有一定的抑制作用,表现为覆土条件下的渗透系数略小于纯土的渗透系数。为进一步定量分析土工织物对不同级配充填砂渗透系数的影响,本文选用南-55 型渗透仪,采用常水头试验方法,探究土工织物对不同颗粒级配充填砂渗透系数的影响,并提出土工织物覆砂系统渗透系数的计算方法。
1 试验材料及试验过程
1.1 试验材料
1.1.1 填充材料
试验所用天然石英砂,砂料按粒径分为小于0.075 mm 的粉粒,0.075~0.125 mm 的细粒,0.125~0.180 mm 的中粒,0.180~0.300 mm 的粗粒,以及粒径介于0.300~0.600 mm 的特大颗粒。由于特大颗粒相较于其他粒径的颗粒对渗透系数的影响可以忽略不计,因此可同时调节特大颗粒与某粒径颗粒的含量,用于探究该粒径的颗粒含量对渗透系数的影响。在严格控制充填料孔隙率和总质量不变的前提下,依次将各粒径含量从10%~50%进行调节,颗粒级配曲线如图1所示。

图1 颗粒级配曲线Fig.1 Particle grading curve
1.1.2 织物材料
渗透试验所采用的土工织物与潮汐河口地区的上海陈行水库和青草沙水库等工程建设中所用的有纺土工织物都为聚丙烯编织布,其基本物理性质指标为:单位面积质量为150 g/m2,厚度为1.20 mm,横纵向断裂强度为375 N/m,横纵向标准强度对应伸长率为50%,CBR 顶破强力为1 600 N,横纵向撕破强力为210 N,等效孔径为0.07 mm。
1.2 试验过程
为保证试验数据的可靠性,采用科研试验中常用的南55型渗透仪,试验操作按照《土工试验规程》[19]中的具体步骤进行,分别开展了有纺土工织物覆砂和纯砂条件下的常水头渗透试验。试验装置如图2所示,仪器的进水口连接能持续提供常水头水压的进水箱,出水口下方放置集水箱。纯砂试验中,渗透仪内仅装填砂料,控制孔隙率为30%;土工织物覆砂试验中,渗透仪内装填砂料后还需在砂料上方满铺土工织物。在试验开始后,待仪器出水管口处流速达到稳定时开始记录数据;当水压稳定后,停止试验。本文通过下述公式对试验结果进行数据处理,计算出各试验组的渗透系数。

图2 渗透试验示意图Fig.2 Schematic diagram of penetration test

式中:k为渗透系数,10-4cm/s;Q为时间t内的渗透水量,cm3;L为两水口间的试样高度,cm;A为过水断面面积,cm2;h为平均水位差,cm;T为时间,s。
2 试验结果及分析
2.1 试验结果
不同级配下的纯砂和土工织物覆砂条件下的渗透系数见表1,纯砂条件下渗透系数为k,土工织物覆砂条件下的渗透系数为k'。
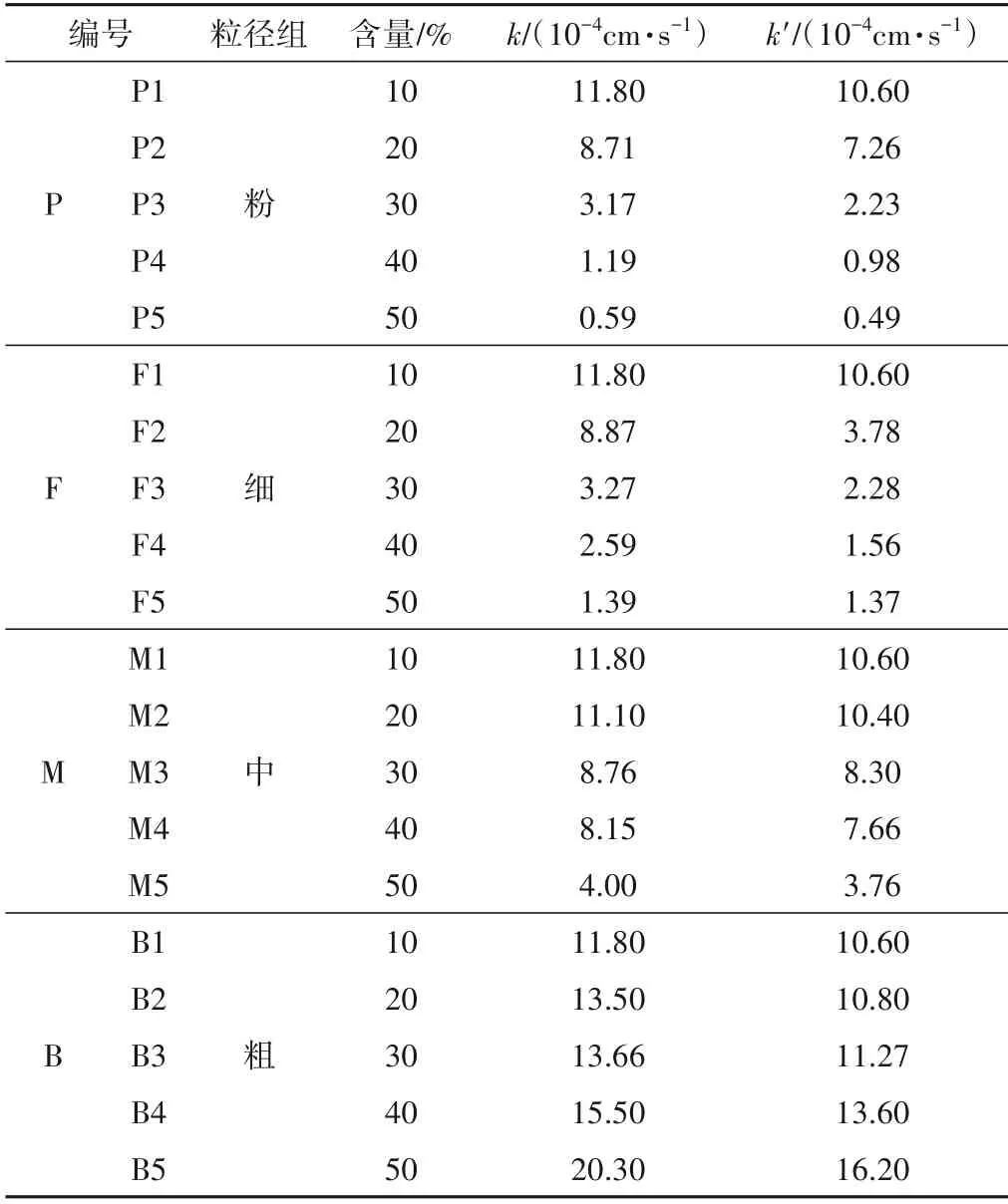
表1 试验结果Tab.1 Test result
2.2 各粒径组对渗透系数的影响分析
2.2.1 各粒径组在纯砂条件下渗透系数的比较
各粒径组在不同含量下纯砂的渗透系数如图3所示,对各粒径组含量与对应渗透系数k进行回归分析,可得到各粒径组含量与渗透系数的拟合公式分别如式(2)~(5)所示。其中kP、kF、kM、kB依次表示在纯砂条件下:粉砂、细砂、中砂、粗砂的渗透系数。
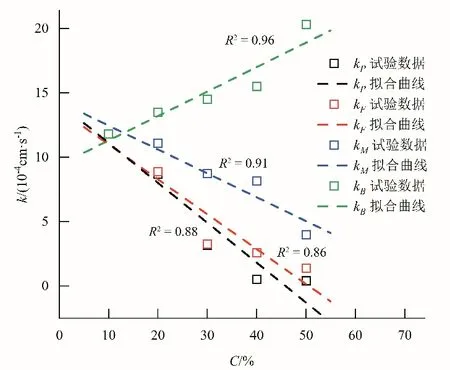
图3 纯砂渗透系数与粒径含量的关系Fig.3 Relationship between permeability coefficient and particle size content of pure sand

从图3中可以看出:随着粉粒含量CP、细粒含量CF和中粒含量CM的增多,中值粒径d50逐渐减小,故渗透系数呈下降趋势。而随着粗粒含量CB的增多,渗透系数kB逐渐上升。其原因可解释为:粗粒含量增多,大颗粒占比变大,小颗粒占比变小,在相同孔隙率下,大颗粒砂之间孔隙无法被小颗粒砂充分填充,从而使砂料之间的填充效果变差,宏观表现为渗透系数增大。
由公式(1)~(4)可知:粉、细、中粒砂含量与渗透系数呈现负相关,粗粒含量与渗透系数呈现正相关关系,且判定系数较高,符合试验现象变化规律。斜率的大小关系为:粉粒>细粒>粗粒>中粒,由此可见,粉粒砂含量的变化对纯砂条件下渗透系数的影响最大,中粒砂含量的变化对纯砂条件下渗透系数的影响最小。
2.2.2 各粒径组在土工织物覆砂条件下渗透系数的比较
各粒径组在不同含量下土工织物覆砂系统的渗透系数值绘于直角坐标系中,并对其数据进行线性回归分析,分析结果如图4所示。并得到相关拟合公式如下:(6)、(7)、(8)、(9)渗透系数的线性回归方程。其中k'P、k'F、k'M、k'B依次表示在土工织物覆砂条件下:粉砂、细砂、中砂、粗砂的渗透系数。

图4 土工织物覆砂渗透系数与粒径含量的关系Fig.4 Relationship between permeability coefficient and particle size content of geotextile covered with sand


由图4可以看出,在土工织物覆砂条件下渗透系数随着粒径含量变化规律一致。
由公式(6)~(9)可知粉粒、细粒、中粒含量与土工织物覆砂条件下的渗透系数呈负相关关系,粗粒含量与渗透系数呈正相关关系,且判定系数较大。比较图4中各趋势线的斜率可知,粉粒砂含量的变化对纯砂条件下渗透系数的影响最大,粗粒砂含量的变化对纯砂条件下渗透系数的影响最小,与纯砂条件下有所差别。
2.2.3 有无土工织物在各粒径组中渗透系数的比较
为进一步明确土工织物在不同粒径组下对渗透系数的具体影响,将图3、4 中所有曲线截取出进行比较分析,如图5所示。

图5 各粒径组不同含量下有、无土工织物覆砂渗透系数的比较Fig.5 Comparison of permeability coefficient of geotextile coated sand with and without different particle size and content
通过图5可知,在各粒径组中,k'均小于k,说明土工织物的存在会降低渗透系数这一结论不受粒径组变化的影响。砂粒的粒径基本大于土工织物的孔隙,故在渗流过程中砂粒难以通过土工织物而被截留,甚至会发生小颗粒聚集产生堵塞的现象,使得土工织物覆砂的渗透系数小于纯砂的渗透系数。比较纵向k与k'的差值可知,在粗粒径组中,土工织物对渗透系数的影响程度最大,说明土工织物对粗粒砂渗透系数的影响最为明显。其原因可解释为:土工织物等效孔径与粉粒粒径基本相等,因此粉粒含量占比较大时,粉粒砂含量是控制渗透系数改变的主要因素;而粗粒含量占比较大时,粗颗粒对渗透系数的影响可忽略不计,此时,土工织物是控制渗透系数的主要因素。
2.3 颗粒级配对渗透系数的影响分析
在试验中采用控制变量法保证孔隙率e和水力梯度j为某一恒定常量,通过改变颗粒级配,得到不同Cc、Cu及d50,各试验组砂料级配指标如表2所示。研究其变化与渗透系数的相关关系,如图6所示。
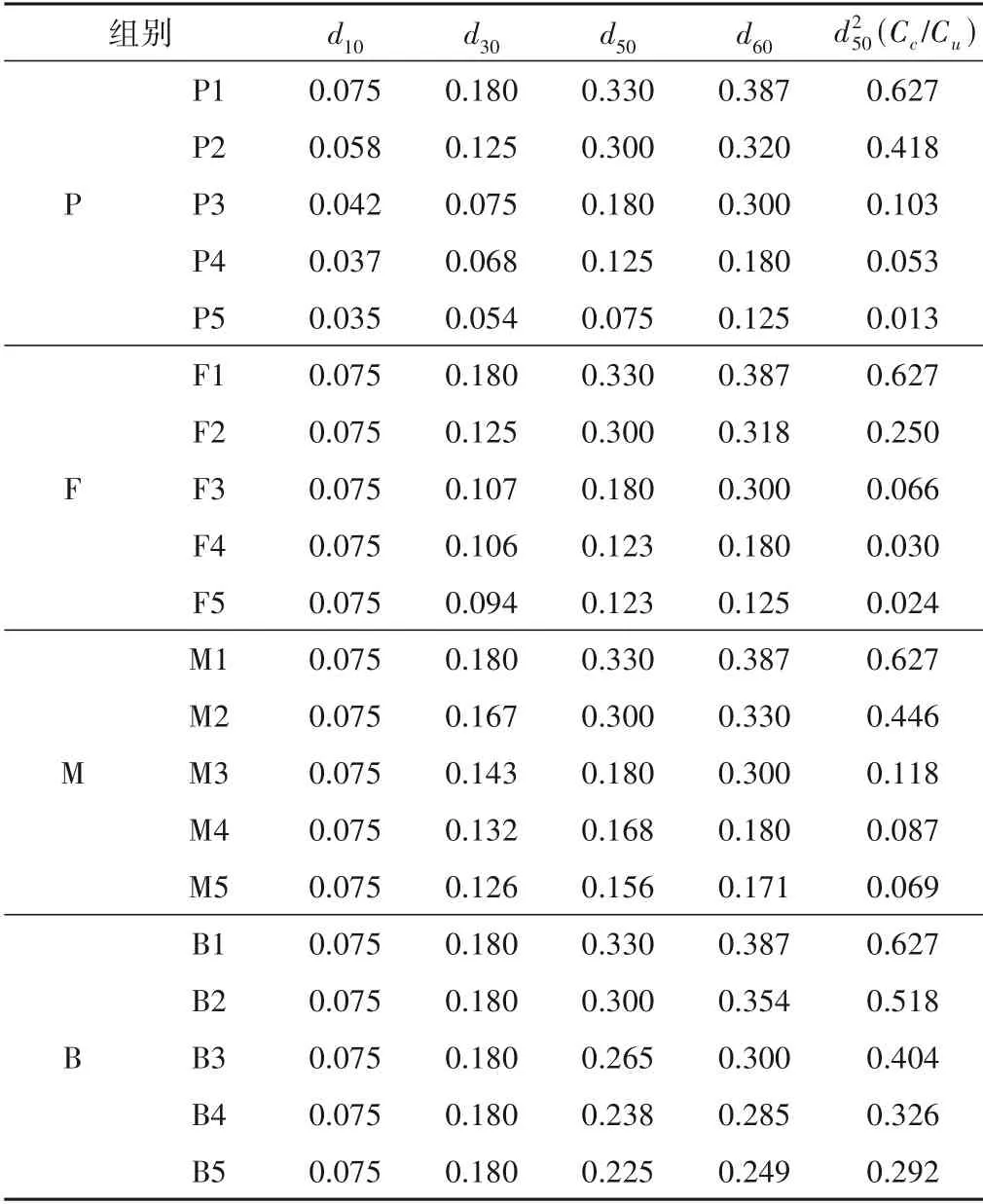
表2 各试验组砂料级配指标Tab.2 Grading index of sand in each test
由图6可知,渗透系数k随d250(Cc/Cu)的增大而增大,且渗透系数与d250(Cc/Cu)呈线性相关。当细粒含量减少,粗粒含量增多时,d50增大,Cc/Cu增大,故d250(Cc/Cu)不断增大,由于孔隙率e不变,即孔隙体积不变,细颗粒无法填充粗颗粒间孔隙的现象愈加明显,故渗透系数增大。

图6 纯砂条件下渗透系数与(Cc/Cu)的关系Fig.6 Correlation between permeability coefficient and(Cc/Cu)under pure sand condition
选择参数d250(Cc/Cu)作为代表颗粒级配的变量拟合得到纯砂条件下渗透系数的经验公式,如(10)所示。

计算出本文纯砂渗透系数的拟合公式计算值kM、文献[12]Hazen公式计算值kH、文献[14]刘杰公式计算值kL、文献[15]朱崇辉公式计算实测值kZ、文献[16]苏立君公式计算值kS与实测值的比值,在3D瀑布图中作出k经验/k实随k实的变化曲线图,如图7所示。

图7 k经验/k随k的变化曲线图Fig.7 Variation curve of k experience/k with k
由图7可知,随着k的变化,k经验/k产生波动,其中波动程度为:kH>kZ>kL>kS>kM,故相较于Haxen 公式、刘杰公式、朱崇辉公式、苏立君公式,本文渗透系数计算公式的计算结果与实测值更为接近。因此,在土工织物覆砂条件下也选用该参数来描述级配与渗透系数的相关关系,如图8所示。使用该参数与渗透系数拟合得到拟合公式如下:

由图8可知,k'与(Cc/Cu)呈线性相关,R²为0.82。可见,该参数在土工织物覆砂条件下,仍具有良好的线性关系。随着(Cc/Cu)的增大,土工织物覆砂与纯砂渗透系数的变化趋势一致,但k始终小于k',说明无论填充料级配优良与否,土工织物始终对充填砂料的渗透功能具有抑制作用。在纯砂条件下,当细粒含量减少,粗粒含量增多时,导致了充填砂料的孔隙截面面积增大,进而使得渗透系数增大;在土工织物覆砂条件下,水流通过土工织物会产生水损,从而使渗透系数减小。故随着(Cc/Cu)的增大,k和k'均增大,且k'始终小于k。

图8 有、无土工织物覆砂渗透系数与(Cc/Cu)关系的比较Fig.8 Comparison of correlation between permeability coefficient of geotextile coated sand and (Cc/Cu)
3 结 论
(1)在有、无土工织物覆砂条件下,单一粒径含量变化对其渗透系数的影响规律一致:粉、细、中、粗粒的含量均与其各自的渗透系数成线性关系,其中粉、细、中粒的含量与渗透系数呈负相关,粗粒含量与渗透系数呈正相关,各相关关系可用公式(2)~(9)分别拟合;在渗流过程中土工织物对于充填砂细颗粒的流失具有一定的抑制作用,因此,土工织物覆砂的渗透系数均小于同条件下纯砂的渗透系数。
(2)在有、无土工织物覆砂条件下,渗透系数与d250(Cc/Cu)均存在较好的线性关系,以该参数为自变量,可拟合得到纯砂的渗透系数计算公式(10)及土工织物覆砂系统的渗透系数公式(11),用于计算不同级配下纯砂及土工织物覆砂系统的渗透系数。
(3)在充填管袋工程设计中,可以通过现场取样并进行室内颗粒级配参数的分析,并结合本文提出的渗透系数计算模型进行渗透系数计算,为充填管袋工程渗流分析提供科学依据。
