酸法地浸采铀多井系统中渗透系数时空演化模拟

2022-07-07陈经明周泽超陈茜茜李寻罗跃

有色金属科学与工程 2022年3期

陈经明，周泽超，陈茜茜，李寻，罗跃

（1.广东华南环保产业技术研究院有限公司，广州 511466；2.核工业二九〇研究所，广东韶关 512029；3.江西省勘察设计研究院，南昌 330095；4.东华理工大学，南昌，330013）

开发铀资源，需要有高效采铀工艺技术。经过多年实践证明，原地浸出采铀（简称地浸采铀）技术具有显著优势，该技术不需井巷工程、不需要建立矿石、废石场，生产成本低、对地表生态环境破坏小、能适应于低品位铀矿开采，是国内外铀矿采冶的主流技术之一[1-5]。由于地浸采铀技术优势明显，不适合地浸的南方硬岩型铀矿，已相继政策性停产。新疆、内蒙古等地相继发现多个适合地浸的砂岩型铀矿后[6]，我国铀资源采冶已基本采用地浸方式采铀。因此地浸采铀已成为我国提高铀产量的重要技术，甚至是唯一技术。

地浸采铀技术基本原理是：首先通过注液井向含矿含水层中注入溶浸液，让其与矿石充分接触，使铀矿溶解于地下水中，然后通过抽液井将富含溶解态铀的地下水抽出，最后将抽出的地下水（称为浸出液）输送至浸出液处理厂提取铀，尾液将作为溶浸液又注入含水层中，形成地下水抽注循环（图1和图2）。按照溶浸液使用的试剂不同将地浸分为酸法、碱法和中性，其中酸法使用硫酸作为溶浸液（图2），使用较普遍。

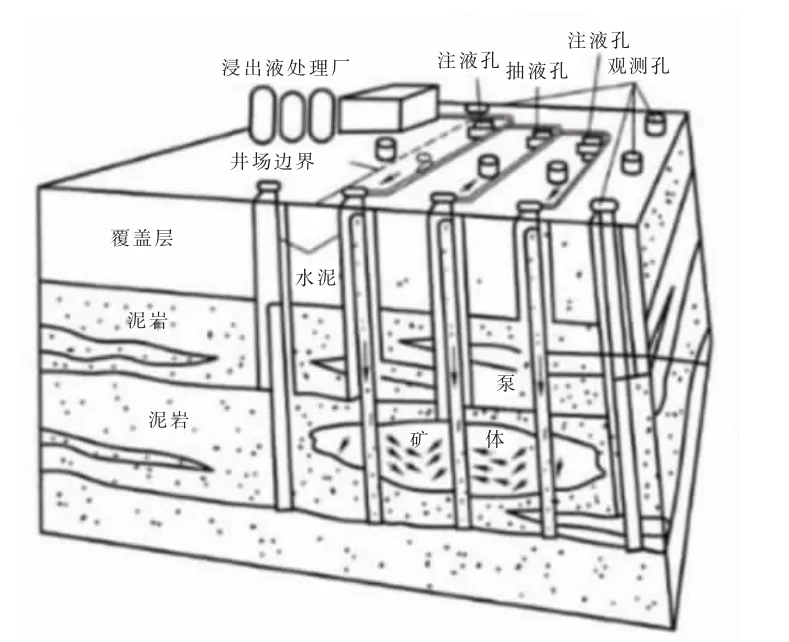
图1 地浸采铀原理示意Fig.1 Principle of in-situ leaching uranium

图2 酸法地浸采铀过程中地下水抽注循环示意Fig.2 Schematic diagram of groundwater extraction cycle during acid in-situ leaching uranium

溶浸范围内抽注井网布设与钻井生产能力、矿层连续性及渗透性等因素有关，目前各个铀矿抽注孔数量主要根据单孔抽注液量及水文地质试验结果来确定[7-8]。地浸井场钻孔布设类型主要有网格式和行列式2种，网格式主要有五点型（四注一抽）和七点型（六注一抽）2种，行列式抽注井各自成行平行排列[9]。

目前国内外关于地浸采铀模拟的研究较少，大部分学者进行的是现场或者室内试验，在实验的基础上建立模型研究。赵春虎等较早提出了将数值模拟应用于地浸采铀中，利用数值模拟软件Visual MODFLOW模拟研究了我国某地浸矿山中水动力场与溶质运移过程[10-11]。周义朋等通过结合现场试验利用数值模拟研究了某砂岩型铀矿床地浸过程中NO3-的运移情况[12]。田亮等模拟研究了某矿山地浸试验流场SO42-的运移规律[13]。何智等通过成熟的地下水数值模拟软件GMS模拟研究了某铀矿床中地下水溶质运移规律，同时预测了未来一段时间内该采区浸出铀浓度变化[14]。焦友军等对比模拟研究了地下水含水层中六价铀吸附反应模型[15]。陈茜茜等通过PHT3D对酸法地浸过程中在低含氧情况下铀水解与迁移的时空演化规律进行了模拟研究[16]。王兵等利用PHT3D模拟分析了酸法地浸采铀中不同酸度对铀矿浸出效率影响，及杂质矿物对溶浸液的消耗降低铀矿浸出率[17]。邱文杰等利用TOUGHREACT模拟研究了地浸采铀过程中溶浸液与矿层水-岩相互作用及反应动力学过程[18]。

大部分学者对于地下水的模拟研究更多的着重点是地下水渗透系数的模拟。桂勇等模拟研究了单孔原地浸矿的渗流量计算模型，结果表明计算模型稳定有效[19]。张将伟等利用不确定分析构建了地下水与地表水耦合模型，确定了渗透系数等参数在模型中的灵敏度较高[20]。赵勇胜等模拟研究了低渗透系数非均质含水层中污染物迁移规律[21]。金磊等通过开发多孔介质渗流耦合模拟平台，揭示了介质渗透性降低的本质是渗流与介质颗粒骨架耦合作用结果[22]。马鹏飞等构建的近场多孔介质渗透模型，可应用于多孔介质渗流过程模拟[23]。

巴彦乌拉铀矿是内蒙古开发的第一个酸法地浸砂岩型铀矿山，自2015年8月正式投产运营以来，矿层渗透性显著降低，导致铀浸出量下降，浸铀成本增高，资源回收率降低，严重阻碍了该矿床的铀资源开发。本文以巴彦乌拉铀矿床矿层堵塞为背景，采用数值模拟法，计算地浸采铀过程中矿层渗透系数的时空演化，预测堵塞发生的时间和位置,为矿区开采过程中解决堵塞等问题提供科学依据。

1 研究方法

1.1 模拟软件

TOUGH（Trransport of Unsaturated Groundwater and Heat）是由美国劳伦斯-伯克利国家实验室基于MULKOM模拟程序开发的数值模拟程序；是一个可以模拟裂隙或孔隙介质中一维到三维的多组分、多相流及非等温的水流和热运移的数值模拟程序，不同程序及所适用的领域如表1所列。本文所用到的数值模拟软件TOUGHREACT是由许天福等基于TOUGH基础上开发的可应用于裂隙或孔隙介质中一维到三维的多组分、多相流及非等温的水流和热反应运移的数值模拟程序[25-26]，不同程序及所适用的领域如表2所列。TOUGH系列软件自开发以来被应用于饱和-非饱和带地下水科学、环境影响评价和修复、地热开发工程、CO2地质封存、核废物处置、白云石化、页岩气及石油开采等领域[27-34]。

表1 TOUGH家族代码的发展历史（自施小清（2009）修[24]）Table 1 Development history of TOUGH family codes(repaired from Shi(2009)[24])

表2 TOUGHREACT模块功能（自XU（2004）修[35]）Tab le 2 TOUGHREACT module function(repaired from XU(2004)[35])

1.2 控制方程

本文相应控制方程均引TOUGHREACT模拟软件使用说明[25]。在TOUGHREACT中的质量守恒示意图如图3。

图3 质量（能量）守恒示意Fig.3 Conservation of mass(energy)

质量守恒方程可以写成以下形式：

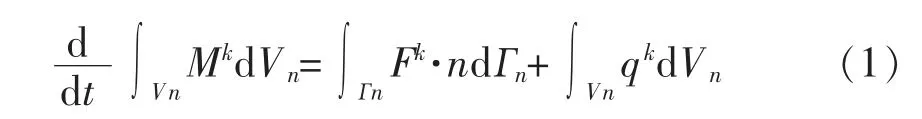
式（1）中：Vn为研究区内的任何积分子区域；Гn为积分区域表面,m2；M为单位体积的能量或质量；k表示不同的组分，如：水、气、溶质等；F为质量(能量)对流量,m3/s；q表示源汇相；n表示通过表面积为dΓn的法向量。

式（2）中：k表示组分；Φ表示孔隙度；Sβ表示β相的饱和度；ρβ表示β相的密度,kg/m3；Xkβ表示在相β中组分k的质量分数；β表示液相。

式（5）中：μβ表示β相渗流速度，m/s；k表示绝对渗透率，m/s；krβ表示相对渗透率,m/s；μβ表示液体黏滞系数,Pa；g表示重力加速度常量，g/s2。

式（6）中：Pβ表示液相压强，Pa；P为参考系压强，Pa；Pcβ为毛管压强，Pa。

所采用的反应速率表达式来自Lasaga等的研究成果[36]。

式（7）中：n表示矿物;rn表示反应速率，（mol/（L·s-1）），正表示溶解，负表示沉淀;kn表示随温度变化的速率常数（mol/（m2·s-1））；An表示每千克水的矿物比表面积（cm2/g）；Ωn表示矿物饱和比率；θ与η由实验得出，通常取1。

式（8）中：k25表示25℃的速率常数，mol/（m2·s）；Ea为活化能，kJ/mol；R为气体常数，kJ/（mol·K），通常取8.314 51；T表示绝对温度，K。

渗透率k（Permeability）表征岩层对不同流体的固有渗透性能，渗透率仅取决于岩石的空隙性质，与渗流的液体性质无关。渗透率与渗透系数K的关系为[37]：

式（9）中:ρ为液体密度，kg/m3;g为重力加速度,m/s2;μ为液体动力黏滞系数,N·s/m2;k为渗透率,常用单位为μm2（即达西）或cm2。

在进行多场耦合建模时需要给定不同物理参数之间的关系，如孔隙度-渗透率之间的关系[38]。孔隙度-渗透率之间复杂的关系取决于孔径分布、孔隙形状及孔隙间的连通性等因素的相互作用，无法仅仅通过简单的立方根定理和Konzeny-Carman孔隙度-渗透率方程反映[39]。有室内实验表明，产生适量的沉淀物会导致孔隙度减少且渗透系数会大幅降低[40]。现场实验表明介质渗透率对于孔喉变化较为敏感[41]，这与在天然情况下渗流通道的收敛-发散性一致，由于孔喉被沉淀物堵塞，导致介质中存在不连续的孔隙空间[39]。渗透率降低不仅取决于总孔隙度的减少，同时也取决于孔隙空间几何形状和沉淀物的空间分布有关[42]。模型中采用VERNA等改进的孔隙度-渗透率关系式[39]。

Verman—Pruess模型：

式（10）中:ki和φi分别表示初始条件的渗透率和孔隙度；φc表示临界孔隙度，当孔隙度达到这个值时渗透率为0；n表示幂指数；φc和n的取值由介质的性质决定。

根据式（9）、式（10）可得渗透系数与孔隙度之间的关系，如式（11）：

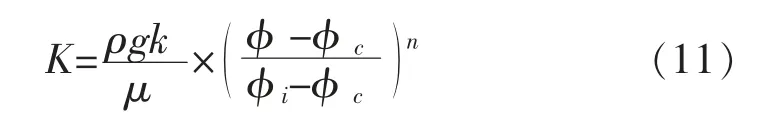
本文中孔隙度初始值取0.2；前人的研究认为当多孔介质中孔隙度约20%时，渗透系数会降低几个数量级[43]，因此φc临界孔隙度取初始值的80%即0.16；渗透率为8.03×10-12m2；由此可确定模型中渗透系数（K，m/d）与孔隙度的关系式为：

渗透系数与孔隙度关系曲线见图4。

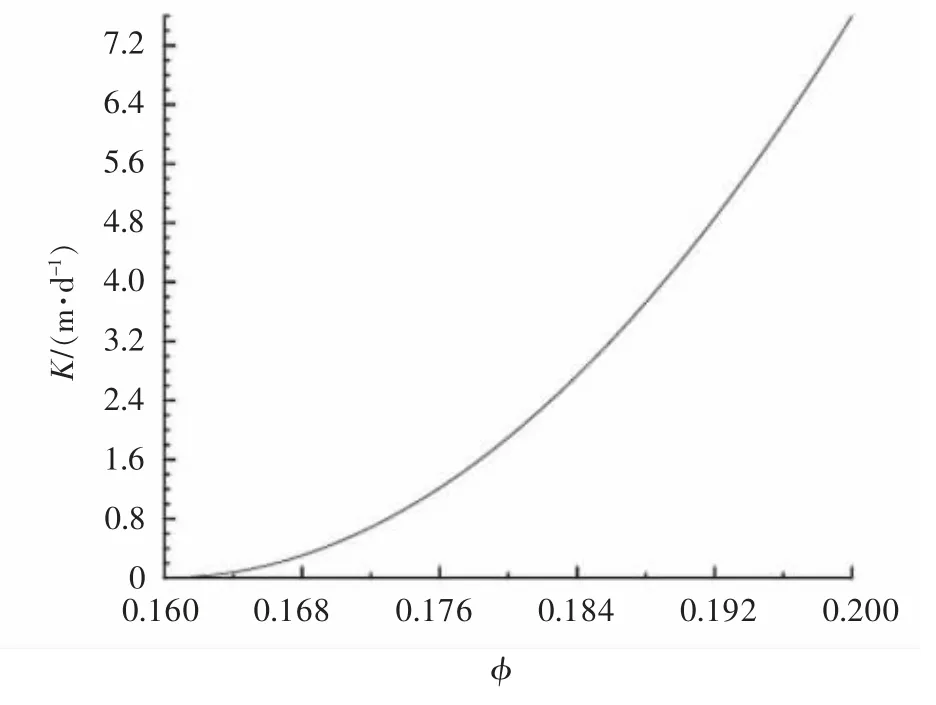
图4 渗透系数—孔隙度关系Fig.4 Relationship between permeability coefficient and porosity

2 数值模拟

2.1 模型概化

基于内蒙古某砂岩型铀矿的多个抽注系统，模拟酸法地浸采铀过程中出现渗透系数减小的现象。该场地的地下水动力场以及地浸采铀的堵塞物质已有详细研究[44-45]。模型共有6个注液孔（Z1-Z6），2个抽液孔（C1、C2）（图5），构成两组五点型二维地浸抽注系统；在确定模拟区域时分别模拟了边长为2 000、1 000、500、200 m正方形区域，模拟结果显示溶浸液的渗流范围较小（图6模拟结果流场图），为了减少模拟时所需的计算量最终确定将边界大小为200 m较为合适。

图5 二维模型概念示意Fig.5 Schematic diagram of the 2-D model

图6 二维流场矢量示意Fig.6 Vector diagram of two-bit flow field

2.2 模型条件

本研究的模拟条件来自郑和秋野等对巴彦乌拉铀矿现场地浸的条件试验和地浸场水动力模拟。模型边界大小确定为200 m，含矿含水层厚度为58.3 m，每个注液孔与抽液孔的距离为30 m，每个注液孔的注入流量为4 m3/h，抽液孔抽出流量为12 m3/h；含矿层厚度58.3 m，含矿层的初始孔隙度假设为0.2，初始渗透系数为7.6 m/d（渗透率为8.03×10-12m2）,总模拟时间为690 d。在地浸采铀中将尾液中的有用元素（铀）沉淀之后，再次作为溶浸液注入注液孔，这种工艺也称为循环抽注系统。这种工艺容易造成矿层渗透系数减小（甚至堵塞），原因是回灌到矿层中的地浸尾液矿化度较高。通过对区域地浸尾液室内试验数据的分析得出：研究区域地浸开采100 d左右后，浸出液中的主要离子浓度趋于稳定（尤其是Ca2+、Mg2+），因此模型中的边界条件各类离子浓度采用100 d后的平均值。初始条件与边界条件的各离子浓度列于表3。根据已有的资料整理得到模拟区域杂质矿物含量列于表4，用于计算矿物动力学速率常数的参数列于表5。

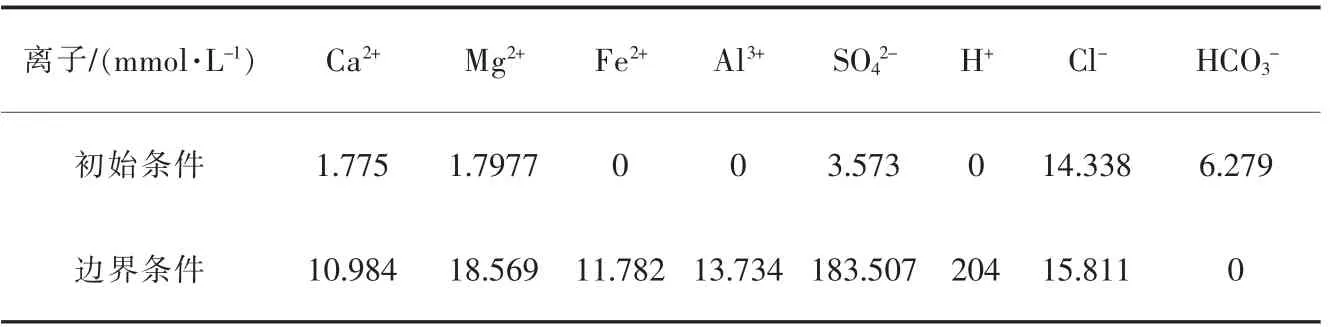
表3 模型初始/边界条件Table 3 Model initial/boundary conditions

表4 模拟区域杂质矿物含量Tab l e 4 Impurity mineral content in the simulated area

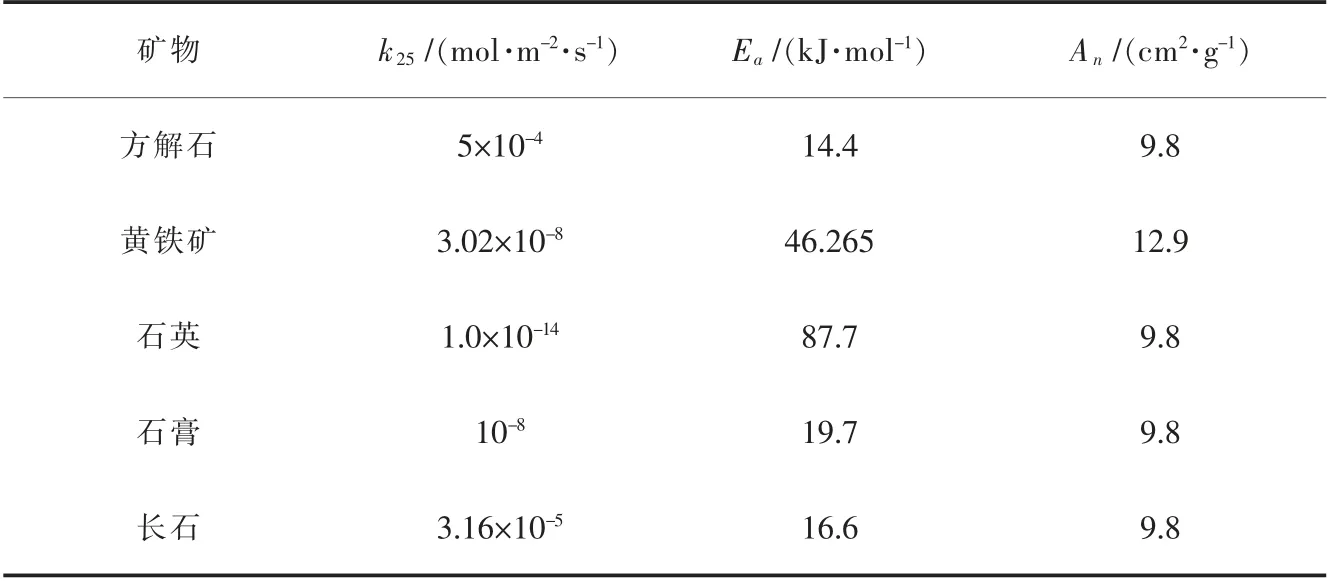
表5 用于计算矿物动力学速率常数的参数Tab le 5 Parameters for calculating the kinetic rate contents of minerals

3 模拟结果与讨论

基于模型概化，选取模拟结果中各因子变化较明显时刻，进行讨论分析；对模拟结果中渗透系数（K）的时空演化规律进行讨论分析。模拟结果中各因子变化较明显的时间分别为：6.9、41.4、200、283、469、690 d；同时选取剖面A、B对渗透系数的空间演化结果进行讨论分析。

3.1 不同时刻渗透系数演化结果

在t=6.9 d时，模拟区域内的渗透系数均大于初始值（7.6 m/d），渗透系数介于7.6~7.69 m/d之间，变化量较小，相对初始值最大仅增大1.2%。渗透系数最大值均位于注液孔附近，与注液孔距离约4 m。在抽液孔附近的渗透系数几乎不发生变化。从图7中可以看出渗透系数发生变化的区域也主要集中在注液孔附近，最大变化半径约为10 m，且变化方向朝着注液孔一侧。

图7 不同时刻渗透系数演化结果Fig.7 Evolution results of permeability coefficient at different times

在溶浸液（H2SO4）反应前锋作用下与注液孔距离越大，渗透系数越接近初始值，不同注液孔周围的渗透系数演化情况相似，没有井群干扰现象。

与上一个时刻（6.9 d）对比，在t=41.1 d时模拟区域内渗透系数发生变化的面积有所增大，且该时刻开始出现渗透系数小于初始值的网格点，以注液孔为圆心渗透系数发生变化区域最大半径为22.63 m。

根据图7可知，t=41.1 d时模拟区域渗透系数介于6.65~7.75 m/d之间；渗透系数最大值和最小值较初始值分别增大2.0%和-12.5%。

说明随着时间的推移模拟区域内的渗透系数区间会不断扩大，并且主要的变化是渗透系数最小值会不断减小，从图7中可以看出，在渗透系数改变的区域内，主要表现为渗透系数不断减小，仅有少量紧邻注液孔的位置渗透系数增大。

根据图7给出的t=200 d模拟区域渗透系数演化结果可知，在该时刻模拟区域内渗透系数介于5.99~9.08 m/d之间，相对初始值最小值减少21.14%，最大值增大19.54%。

从图7中可以看出，模拟区域内渗透系数增大的范围仅出现在靠近注液孔周围的极小区域内（半径约为4 m），沿溶浸液渗流范围内的其他区域均出现了渗透系数减小现象。通过与之前的几个时刻（6.9 d、41.4 d）对比，说明在模拟区域内靠近注液孔处的矿层随着时间的延长不断与溶浸液发生溶解反应，且在渗流作用和反应动力学共同作用下，在渗流路径中不断会有沉淀物生成，同时也有溶解反应发生。

根据模拟结果显示，该时刻渗透系数小于初始值的大部分矿层内渗透系数均介于5.99~6.77 m/d之间，少部分区域渗透系数介于7.15~7.45 m/d之间。

从模拟结果可知在抽液孔附近（半径小于2 m）渗透系数已经开始发生变化。说明模拟到200 d时，溶浸液与杂质矿物发生的沉淀-溶解反应已经开始影响抽液周围的渗透系数。且与注液孔距离越远渗透系数减少值则越小，说明在渗流通道上沉淀-溶解量不断发生变化；与注液孔距离近的区域沉淀物的量较多，溶解量较少；靠近抽液孔处沉淀量相对减少，溶解量也相对增加。

图7给出了t=283 d模拟区域渗透系数演化结果，t=283d时模拟区域内渗透系数区间为5.88~9.44 m/d。最大值相对初始值增大了30.34%,最小值相对初始值减小了22.61%。对比前文中讨论的几个时刻，该时刻最大的区别是模拟区域内渗透系数的最大值变化量比最小值变化量大。

渗透系数最大值（9.94 m/d）均出现在注液孔附近，且渗透系数发生变化的范围几乎没有变化；从模拟结果图可以看出该区域内渗透系数均大于7.9 m/d。说明在注液孔附近渗透系数增大的区域内，不断发生溶解反应，产生的离子随渗流通断不断运移；在该区域内矿物溶解量远大于沉淀量。

从图7可知该时刻渗透系数发生改变的区域内只有少部分区域渗透系数区间为[7.4 m/d,7.9 m/d]，说明在模拟达到283 d时，矿层内发生沉淀和溶解的区域分界线较明显。

在渗透系数发生改变的区域中渗透系数介于区间为[5.88 m/d,6.9 m/d]的区域占比较大。说明在这些区域内，反应生成的沉淀物量大于溶解量；且该区域内大部分位置渗透系数均小于6.39 m/d，只有少量靠近抽液孔处区域的渗透系数为6.9 m/d。

随着模拟时间不断增加，渗流场-化学场耦合作用对模拟区域内的渗透系数以及其他因子影响越明显。

图7给出496 d时的渗透系数演化结果，该时刻矿层内渗透系数最大值为12.01 m/d，相对初始值增大了57.99%；渗透系数最小值为5.65 m/d，相对初始值减小了25.71%。

在前文中讨论到283 d时模拟区域渗透系数在两组五点型抽注系统的影响范围有公共区域，从模拟结果看出，该时刻（496 d）渗透系数在模拟区域内分布较均一。在渗透系数减小的区域内，不同抽注液孔之间几乎没有差异；两组抽注系统的渗透系数空间分布关于直线X=100对称，这是之前几个时刻没有出现的情况；说明经过496 d的反应运移，渗流场-化学场相互影响已经开始趋于稳定状态，至少模拟区域内的沉淀物空间分布差异性开始减小。

对于区域内渗透系数增大和减小的区域，与前文的分析相似。区别在于该时刻矿层内渗透系数减小的范围有所增大，这是由于不断注入的溶浸液与伴生矿物反应增加了沉淀物的量，同时也由于反应动力学的作用，沉淀物会在渗流路径中生成，同时可以解释，矿层内渗透系数小于初始值的区域内渗透系数差异性较小。

根据图7给出的模拟结束时（690 d）的渗透系数演化结果，该时刻矿层内渗透系数最大值为14.68 m/d，相对初始值增大了93.18%；渗透系数最小值为5.37 m/d，相对初始值减小了29.31%。

随着时间的推移，矿层内渗透系数改变的区域不断增大。从模拟结果可以看出，模拟区域内渗透系数发生改变的区域主要集中在抽注液孔之间，在注液孔外侧也有部分区域渗透系数减小。从图7可知，注液孔Z1、Z3、Z4、Z6演化情况一致，Z2、Z5演化情况一致。

渗透系数区间值不断增大，模拟结束时（690 d）渗透系数最大值（14.68 m/d）是最小值（5.37 m/d）的2.73倍，且渗透系数增大的区域除了集中在注液孔附近，在外侧也有少量位置渗透系数所有增大；渗透系数减小的区域不断增大。由于不断注入的溶浸液与杂质矿物发生反应，在注液孔处大量的杂质矿物发生溶解反应，但是在反应动力学的作用下沉淀反应不会马上发生，因此沉淀物会分布在渗流通道上。对于渗透系数减小的区域内，也会有溶解反应生成，但是模拟结果显示生成的沉淀物量大于溶解量。

对比前文中讨论的几个时刻，模拟结束时最大的特点是在渗透系数减少的区域外侧，有少量区域的渗透系数相对初始值有所增大（8.86 m/d）。分析可能的原因是这些区域也是渗流场影响的范围内，运移到这些网格的溶浸液内还有少量的H+未反应，与矿层发生反应导致渗透系数增大。

图7给出了不同时刻（6.9、41.4、200、690 d）二维模型渗透系数演化结果。从演化结果来看，渗透系数发生变化的区域随时间不断增大，模拟区域内渗透系数范围随时间不断增大。

在渗流作用和化学反应前锋不断向抽液孔推进，井群干扰现象越明显，6个注液孔周围的渗透系数演化情况略有差异。Z1、Z3、Z4、Z6 4个注液孔演化情况相似，从图中可以看出渗透系数变化主要方向不断向C1或C2抽液孔推进；Z2、Z5 2个注液孔演化情况相似，从图7中可以看出渗透系数变化主要方向不断同时向C1和C2抽液孔推进。出现这种情况的原因是C1、C2共同影响Z2、Z5注液孔周围的流场分布，其他4个注液孔周围的流场仅受C1或者C2单独影响。

3.2 不同空间渗透系数演化结果

图8给出了两个剖面（A、B）渗透系数在t=6.9 d、t=41.4 d、t=200 d、t=283 d、t=469 d及t=690 d时的演化结果。0 m表示注液孔位置，30 m表示抽液孔位置。

从图8中可以看出在A、B两个剖面中，从注液孔到抽液孔之间的渗透系数演化情况相同之处是：渗透系数随距离的总体趋势均是不断减小；在d=17.23 m到注液孔处两组抽注孔之间的渗透系数演化结果相同。

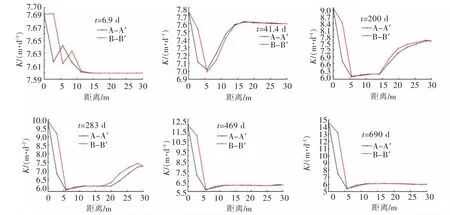
图8 不同空间位置渗透系数演化结果Fig.8 Evolution results of permeability coefficients at different spatial locations

不同之处：A和B两个剖面上渗透系数在该时刻演化结果有所差异。A剖面上渗透系数区间为[7.60 m/d，7.68 m/d]，B剖面上渗透系数区间为[7.60 m/d,7.69 m/d]。

在d=17.23 m之前两组抽注孔之间的渗透系数演化虽然是沿渗流路径不断减小，但是相同距离下的渗透系数均不相同；在d=17.23 m之前的渗流路径内大部分（占抽注液孔间距的81.7%）位置中Z2-C1之间的渗透系数大于Z4-C1之间的渗透系数。

根据图8给出的两个剖面（A、B）渗透系数在t=41.4 d时演化结果。对比2个剖面渗透系数演化结果，相同点是：两个剖面上渗透系数沿渗流路径的演化趋势相同，均是先减小后增大；两个剖面上该时刻渗透系数最小值出现的位置相同（均是于注液孔相距5.58 m处）；两个剖面在14.82 m之后的空间位置上渗透系数差异较小。

在A、B两个剖面上从注液孔到渗透系数最小值处（5.63 m处）之间区域内也有所差异，A剖面上渗透系数沿渗流路径不断减小，B剖面从注液孔（7.50 m/d）到2.83 m（7.53 m/d）之间有所增大且均小于初始值。

两个剖面上渗透系数演化的不同点：两个剖面上渗透系数最小值有所不同，其中A剖面上渗透系数最小值为7.02 m/d，B剖面上渗透系数最小值为6.99 m/d。

A剖面在靠近注液孔处的渗透系数大于初始值（7.75 m/d），在B剖面上靠近注液孔处的渗透系数小于初始值（7.50 m/d）。

两个剖面从注液孔到5.88 m处两个剖面上渗透系数差异性较大，主要体现在B剖面不同位置渗透系数演化较复杂，从注液孔处出发有少量位置的渗透系数相对注液孔出有所增大；从5.58 m至抽液孔处渗透系数演化也有所差异，B剖面大部分空间位置的渗透系数均小于A剖面相同位置。

根据图8给出的两个剖面（A、B）渗透系数在t=200 d时演化结果。A、B两个剖面渗透系数最小值均出现在5.66 m处，该时刻两个剖面上渗透系数最小值差异较小（A剖面渗透系数最小值为5.99 m/d，B剖面渗透系数最小值为6.05 m/d，相差1%）；两个剖面上渗透系数演化结果均出现了大于初始值和小于初始值的空间位置。

A和B两个剖面上渗透系数在该时刻演化结果有所差异。A剖面上渗透系数区间为[5.99 m/d，9.08 m/d]，B剖面上渗透系数区间为[6.05 m/d，8.41 m/d]，B剖面上出现了渗透系数明显大于初始值的位置，A剖面上渗透系数区间明显大于B剖面上渗透系数区间，说明B剖面上的渗透系数较A剖面渗透系数演化较慢。

模拟结果看出在该时刻A、B剖面大部分位置处，B剖面上的渗透系数率大于A剖面上的渗透系数（注液孔除外）；14.15~30 m之间的区域内，B剖面上渗透系数值曲线一直在A剖面渗透系数值曲线上方；在5.63~14.15 m之间存在少部分区域（约2.81 m）B剖面上渗透系数值曲线一直在A剖面渗透系数值曲线下方。

图8给出的两个剖面（A、B）渗透系数在t=283 d时演化结果。A、B两个剖面渗透系数最小值均出现在5.66 m处，该时刻两个剖面上渗透系数最小值差异较小（A剖面渗透系数最小值为5.88 m/d，B剖面渗透系数最小值为6.94 m/d，相差1%）。

A和B两个剖面上渗透系数在该时刻演化结果有所差异。A剖面上渗透系数区间为[5.88 m/d,9.94 m/d]，B剖面上渗透系数区间为[5.94 m/d,9.17 m/d]，B剖面上出现了渗透系数明显大于初始值的位置，A剖面上渗透系数区间明显大于B剖面上渗透系数区间，说明B剖面上的渗透系数较A剖面渗透系数演化较慢；在该时刻，两个剖面在渗透系数较小的区域内（5.66~16 m）之间的演化情况一致。

两个剖面渗透系数演化的差异性体现在靠近注液孔处，以及16~30 m这两段区域内；在16~30 m之间，B剖面渗透系数均大于A剖面上相同位置处的渗透系数，注液孔到5.66 m之间两个剖面上渗透系数的差异与前文中讨论一致，就不赘述。

图8给出的两个剖面（A、B）渗透系数在t=469 d时演化结果。A、B两个剖面渗透系数最小值均出现在5.66 m处，该时刻两个剖面上渗透系数最小值差异较小（A剖面渗透系数最小值为5.88 m/d，B剖面渗透系数最小值为6.94 m/d，相差0.8%）；在该时刻，两个剖面从渗透系数最小值到抽液孔处（5.66~30 m）之间的演化情况一致。

A和B两个剖面上渗透系数在该时刻演化结果有所差异。A剖面上渗透系数区间为[5.65 m/d,12 m/d]，B剖面上渗透系数区间为[5.70 m/d,10.94 m/d]，B剖面上出现了渗透系数明显大于初始值的位置，A剖面上渗透系数区间明显大于B剖面上渗透系数区间，说明B剖面上的渗透系数较A剖面渗透系数演化较慢。

通过两个具有代表性的剖面渗透系数演化结果可知，在该时刻，模拟区域内大部分空间位置的渗透系数均小于初始值。

根据图8给出的两个剖面（A、B）渗透系数在t=690 d（模拟结束）时的演化结果。A、B两个剖面渗透系数最小值均出现在5.66 m处，该时刻两个剖面上渗透系数最小值差异较小（A剖面渗透系数最小值为5.37 m/d，B剖面渗透系数最小值为5.42 m/d，相差1.11%）；在该时刻，两个剖面在渗透系数较小的从渗透系数最小值到抽液孔处（5.66~30 m）之间的演化情况一致。

A和B两个剖面上渗透系数在该时刻演化结果有所差异。A剖面上渗透系数区间为[5.37 m/d，14.68 m/d]，B剖面上渗透系数区间为[5.42 m/d，13.20 m/d]，B剖面上出现了渗透系数明显大于初始值的位置，A剖面上渗透系数区间明显大于B剖面上渗透系数区间，说明B剖面上的渗透系数较A剖面渗透系数演化较慢。

在该时刻，模拟区域内仅有注液孔出的渗透系数大于初始值，且从模拟结果看出，在溶液渗流通道内大部分区域的渗透系数均在6 m/d左右。

通过对比模拟区域内两个剖面内渗透系数演化的差异可知，在多组抽注系统共同作用下，不同抽注井之间渗透系数演化差异性随时间推移不断减小。在文中给的抽注系统中，渗透系数最小值出现在与注液孔相距大约5.66 m处；受单个抽液孔影响的注液孔周围渗透系数在渗流路径上演化较为单一，受多个（文中仅有两个）抽液孔影响的注液孔附近渗透系数在模拟初期演化较为多样性；

随着模拟时间的推移，溶浸液渗流通内渗透系数会不断较小，且区域内渗透系数会区域一致。

从选取的两个特征剖面来看，不同抽注系统内渗透系数存在一定的相互影响的现象，随着时间的推移影响越明显，主要体现在模拟末期两个剖面上的渗透系数演化趋于一致，差异性较小。