基于标准化欧式距离的挠度传感器故障诊断方法研究

2022-09-02陈熠昕刘张浩王代林刘诗拓刘怀林

公路交通技术 2022年4期

陈熠昕，刘张浩，王代林，刘诗拓，刘怀林

(1.招商局重庆交通科研设计院有限公司，重庆 400067；2.物康科技有限公司，重庆 404100；3.重庆市万州区市政设施维护管理中心，重庆 404100)

桥梁结构健康监测旨在对大型桥梁的结构性能进行实时监测与损伤诊断，并进行安全评估和性能预测，是近年来土木工程领域研究的热点方向之一[1]，逐步在实践中得到推广。如今越来越多的桥梁布设有健康监测系统，如香港青马大桥、广州虎门大桥、重庆大佛寺长江大桥等[2]。大型桥梁健康监测系统中，传感器子系统是其中不可或缺的组成部分。各种类型的传感器用于获取结构响应和采集各种各样的监测信息，其性能和精度直接影响最终的评估结果。然而，传感器在监测过程中受服役环境和设备寿命的影响，会出现异常和故障，常造成采集数据不准确等问题，若不及时识别排除，会导致虚警或漏警现象发生。若将之直接应用于损伤识别和状态评估，则必然对诊断评估的准确性带来巨大干扰，造成不必要的经济损失，甚至安全危机。

近年来，传感器故障诊断问题已成为研究热点。其研究方向大致可分为传感器故障诊断与传感器故障定位2个方面。传感器故障分类可按故障原因、故障程度、故障表现、故障统计分类等方面进行划分。何富君等[3]按照故障统计分类的指标，将常见故障分为以下4类：卡死、恒增益、固定偏差和线性偏差。YI等[4]综合Kulla[5]的研究成果，将传感器故障类型扩展并划分为以下8类，分别为：偏移、漂移、增益、精度下降、1型完全失效(常量)、2型完全失效(常量+噪声)、跳点和缺失。基于监测数据分析，传感器异常数据诊断方法的底层原理可分为基于解析模型、基于信号处理和基于知识经验3类[6]。目前，基于信号处理的方法在桥梁健康监测系统传感器故障诊断领域的应用范围最广。Reppa V等[7]基于传感器组获取的监测数据，使用由结构化残差和自适应阈值配制的鲁棒分析冗余关系对每个传感器组中的故障进行诊断。唐浩等[8]利用支持向量机SVM(Support Vector Machine)技术对实桥应变监测数据日均值进行建模处理并预测其未来发展趋势。Wang等[9]提出了一种用于融合诊断系统的传感器漏诊的特征值再分配方法，试验结果表明，特征值再分配方法可有效解决传感器容错问题。胡顺仁等[10]通过数据标准化残差分析对桥梁健康监测系统中的传感器进行了故障判定和时间定位。Fu K等[11]在结构化残差的基础上提出改进的动态主元分析PCA(Principal Component Analysis)方法，并定义了传感器的故障灵敏度和临界灵敏度。胡顺仁等[12]将PCA应用在桥梁挠度传感器故障诊断。Huang等[13]根据故障敏感性差异开发了加权PCA方法，利用实验室数据研究了传感器故障定位。安星等[14]改进了PCA现有残差贡献图和残差贡献指标，提升了故障定位的准确率，并将诊断范围从单传感器故障定位扩展到双传感器。

基于信号处理的方法能有效识别并诊断传感器故障，在机械、电气、控制工程的应用较为广泛。在桥梁结构健康监测领域的传感器故障诊断重点多集中于传感器监测值和诊断本身，而忽略其实际工程意义和与传感器具体故障表现的对应关系，对不同监测量的故障数据未进行对应的指标特征分析和故障类型识别，这不利于后续的故障诊断数据修复，限制了信号处理方法在桥梁健康监测系统中的进一步扩展应用。本文旨在从桥梁安全监测、评价的重要参数挠度出发，针对挠度传感器常见病害对应的3类趋势性数据故障表现，利用标准化欧式距离指标，对这3类常见故障进行诊断和特征分析，提升基于信号处理的传感器故障诊断技术在桥梁健康监测领域诊断和定位的准确性、方法的适用性以及后续预警的准确率。

1 理论方法

1.1 数据标准化模型

在健康监测过程中，挠度是桥梁安全状态监测和评价的重要指标之一。为了掌握桥梁结构是否存在异常，常利用连通管系统进行多点挠度同步动态监测。为减小或消除测试误差的影响，除需对监测数据进行消噪滤波外，通常还需对测点挠度数据进行标准化处理，利用标准化数据开展结构性能机制和性能响应研究。挠度监测数据经过标准化处理后被去量纲化，转变为无量纲的数值，便于挠度监测相关测点的对比分析。常见的数据标准化方法有min-max标准化、log函数转换、atan函数转换、z-score标准化、模糊量化法等。结合桥梁挠度传感器数据自身的特性，选用z-score数据标准化方法。

z-score数据标准化的一般模型如下：

(1)

式中：x为数据的原始值；x′为标准化后的新数据；N为采样数据序列的长度；xi为原始值中第1次采样所得的采样数值；u为采样数据的平均值；s2为原始值的方差；s为原始值的标准差。

1.2 时间序列相似性分析

时间序列的相似性分析是基于距离来评价不同信号之间的相关程度，是一种数据挖掘方法。常见的相似性度量标准有欧式距离、曼哈顿距离、余弦相似度、简单匹配系数等。定义X={x1，x2,…,xn}是m维向量空间中的样本集合，其中的2个样本xi，xj分别为xi=(x1i,x2i,…,xmi)T，xj=(x1j,x2j,…,xmj)T，则xi，xj之间的闵可夫斯基距离(Minkowski distance)定义为：

(2)

当p=2时，称为欧式距离：

(3)

运用简单的欧氏距离求出的值将会非常大，且没有实际意义。为此，需对相关挠度测点的数据进行标准化。结合标准化残差的数学模型：

(4)

采用欧几里得距离度量不同时间序列间的相似性，当d(X,Y)越小时，说明2条序列越相似。

(5)

在故障诊断的过程中，若情况正常，相关挠度监测点的数据之间保持较好的相关性，标准化欧式距离维持在一个区间内上下随机波动。当有故障发生时，可从标准化欧氏距离这一指标的趋势和相对值变化表现出来，挠度数据间的强相关性遭到破坏，标准化欧式距离的相对波动程度增大，最终超越正常情况下的标准化欧式距离阈值，这就是基于标准化欧氏距离实现故障诊断的基本依据。对于故障定位，引入故障定位效率这一指标来表征定位的精确程度：

(6)

式中：t为标准化欧式距离超越设定阈值的时间点；t0为故障起始时间点。

1.3 标准化欧式距离故障特征诊断算法流程

标准化欧式距离故障特征诊断算法流程如图1所示。

图1 标准化欧式距离故障特征诊断算法流程Fig.1 Process of standardized Euclidean distance fault feature diagnosis algorithm

1) 数据初始化，确定相关挠度测点及诊断窗宽度。

2) 提取训练挠度测点数据和待测挠度测点数据，对数据进行标准化处理，并基于训练挠度测点数据求取故障诊断阈值。

3) 计算待测挠度测点的标准化欧式距离值，判断其是否超过故障诊断阈值，如已超过，继续进行故障诊断和故障时间定位，并基于式(6)计算故障定位效率，初步评估传感器故障定位效果。

2 数值模型

2.1 传感器常见故障模型

在结构健康监测过程中，异常监测数据一般是指由传感器故障或外界干扰所引起的显著偏离真实结构响应的监测数据。当测量值与真值存在误差范围外的偏差时，传感器会判定为有故障。用x*(t)代表t时刻的待测变量真值，w(t)代表传感器测量噪声，则有传感器显示的正常值x(t)能够被表达为：

x(t)=x*(t)+w(t)

(7)

常见的7类传感器故障数值模型[4]如表1所示，其中a、b、k是描述相关传感器故障程度的常数，e(t)代表由传感器故障导致的均值为零的高斯白噪声干扰。

表1 7类传感器故障数据模型Table 1 Fault data model of sensors of seven types

固定偏差故障多见于挠度传感器突发性的漏液状况；漂移故障与精度下降故障多见于挠度传感器逐渐漏液，或液体自然蒸发的单一或多因素共同作用下的情况。为此，本文针对挠度传感器故障的具体工程表现及对应原因，选取精度下降故障、漂移故障以及固定偏差故障进行研究。

2.2 数值模型简介

本文试验选取的是招商云合川区合阳嘉陵江大桥监测系统数据中的第2跨挠度传感器测试数据，时间从2021年10月16日至2021年11月16日，共计2 632个数据点，采样周期为12 min，为尽量减少温度对传感器故障诊断的影响，选取其中温度变化较为平稳时间区段的600个数据样本点进行分析，每取10个点计算一次标准化欧式距离，直到点600，共计591个时间点数据。

在传感器正常运行的状态下，相关测点2-1和2-2的挠度数据之间具备较强的相关性，其数据标准欧式距离值大部分在区间[0.45,1.22]之间波动，整体数据表现正常，原始数据及对应标准化欧氏距离如图2和图3所示，提取标准化欧式距离的最大值1.211 9作为后续故障诊断阈值。

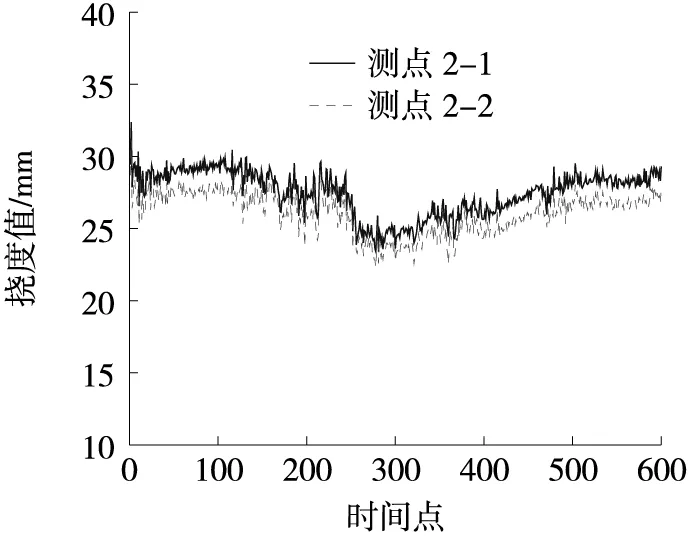
图2 正常情况下相关挠度测点数据Fig.2 Data of relevant deflection measuring points under normal conditions

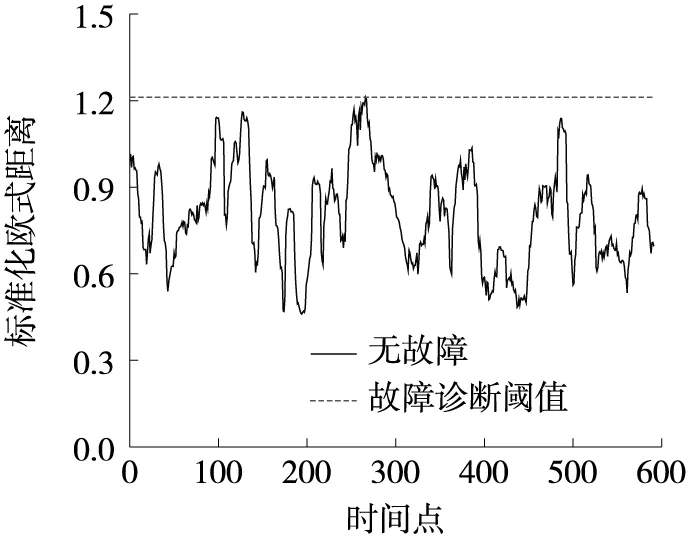
图3 基于标准化欧式距离的无故障检测结果Fig.3 Fault free detection results based on standardized Euclidean distance

2.3 固定偏差故障分析

固定偏差故障表征挠度传感器在某一时刻开始监测值与真值存在一个固定的偏差值，这种故障对应挠度传感器出现漏液的状况。测点挠度监测数据如图4所示。在本次数值仿真试验中，将测点2-2在时间点t=200之后的挠度监测值上加上一个常偏差值a=10 mm，用以模拟固定偏差故障，研究标准化欧式距离这一指标对固定偏差故障的识别效果，并利用该指标来对固定偏差故障进行故障时间定位研究，结果如图5所示。

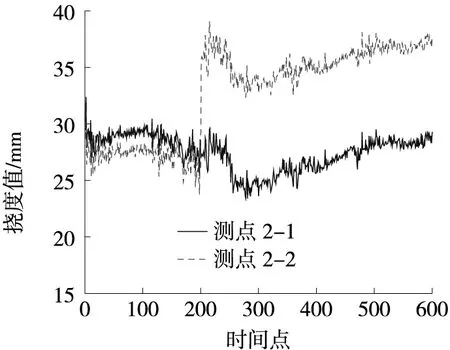
图4 固定偏差故障下相关挠度测点数据Fig.4 Data of relevant deflection measuring points under fixed deviation fault

图5 基于标准化欧式距离的固定偏差故障检测结果Fig.5 Fixed deviation fault detection results based on standardized Euclidean distance

由图4可知，测点2-2的挠度监测数据在t=200之后发生明显增益，2组关联测点监测数据在故障发生后存在明显差异。由图5可知，在故障发生前，即t=1～200时，监测数据标准化欧式距离低于故障诊断阈值，表征该阶段传感器监测数据间相关性强，挠度传感器并未发生故障。故障发生后，标准化欧式距离值在t=200处发生异常跳跃，超出故障诊断阈值，判定挠度监测数据异常，需进行后续预警。综上分析，以标准化欧式距离为指标能初步诊断固定偏差故障，并初步判定固定偏差故障时间。

为进一步研究不同故障程度下的故障诊断和故障时间定位的稳定性，现选取固定偏差值a=3 mm～7 mm，其取值间隔为1 mm，一共5组模拟试验进行分析，结果如图6、图7所示。

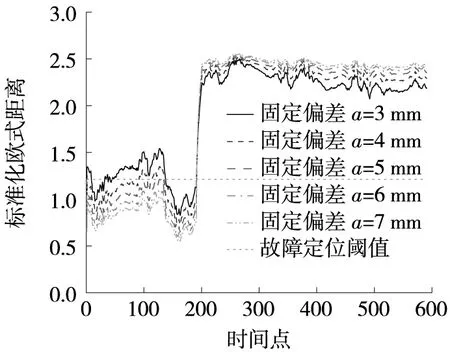
图6 不同偏差值下的固定偏差故障诊断结果对比Fig.6 Comparison of fixed deviation fault diagnosis results under different deviation values

注：柱状图数据对应故障定位效率；点状图数据对应故障定位时间点。

对比分析图6、图7中5组不同偏差值下的故障模拟试验结果发现，在固定偏差为5 mm～7 mm时，可准确诊断和定位固定偏差，故障定位时间点t0=237，故障定位效率L0=81.5%；在固定偏差低于4 mm时，仍能进行故障诊断，但故障定位效率急剧降低，定位效率低于68.2%。总体来说，标准化欧式距离指标基本能够较好地识别固定偏差故障和定位故障发生时间，故障时间定位精度随着固定偏差值的减小而降低，固定偏差a<4 mm时，利用该指标进行固定偏差故障定位，效果并不理想。

2.4 精度下降故障分析

精度下降故障是固定偏差故障的特殊情况，表征挠度传感器监测值在某一时刻开始与真值存在一个随时间变化的偏差值。在本次数值仿真试验中，采用设置信噪比的方式来模拟精度下降对监测数据的影响，将测点2-2在t=200之后的挠度监测值上设置20 dB的信噪比，并利用标准化欧式距离指标开展精度下降故障分析，结果如图8、图9所示。

图8 精度下降故障下相关挠度测点数据Fig.8 Data of relevant deflection measuring points under precision degradation fault

图9 基于标准化欧式距离的精度下降故障检测结果Fig.9 Accuracy degradation fault detection results based on standardized Euclidean distance

由图8可知，在t=200以后，测点2-2的挠度监测数据波动性急剧增加，相关测点2-1的挠度值并未发生剧烈波动。显然，2组关联测点挠度数据在故障发生前后存在明显差异。由图9可知，在故障发生前，即t=1～200时，监测数据标准化欧式距离低于故障诊断阈值(1.2)，表征该阶段传感器监测数据间相关性强，挠度传感器并未发生故障。故障发生后，标准化欧式距离值t=200点附近处较正常值发生异常跳跃，超出阈值范围(1.2)，且故障发生后的数据标准化欧式距离波动幅值较正常阶段更大，判定挠度传感器后续数据异常并进行预警。综上分析，以标准化欧式距离为指标能初步诊断精度下降故障，并能判定精度下降故障时间。

为进一步综合不同的精度下降程度，对故障诊断和故障时间定位的稳定性进行研究。设置信噪比SNR=15 dB～25 dB，其取值间隔为5 dB，一共3组试验进行故障时间定位分析，结果如图10、图11所示。

图10 不同信噪比下精度下降故障诊断结果Fig.10 Accuracy degradation fault diagnosis results under different signal-to-noise ratios

图11 不同信噪比下精度下降故障时间定位结果Fig.11 Fault time location results of accuracy degradation under different signal-to-noise ratios

对比分析图10、图11中3组精度下降的故障模拟试验结果发现，信噪比在15 dB～25 dB之间时，均能准确诊断精度下降和定位故障发生时间，故障定位时间点t0=193，故障定位效率L0=96.5%。综上分析，标准化欧式距离指标在一定范围内能够较好地检测出精度下降故障和定位故障发生时间。

2.5 漂移故障分析

漂移故障是指挠度传感器监测值相对于真实值保持一定线性增长偏差，致使监测值与真实值的距离逐渐增大，监测数据相关性减弱。在本次数值仿真试验中，采用设置漂移速率的方式模拟仿真漂移故障，当漂移速率k=0.05，将测点2-2在t=200之后的挠度监测值上增加一个数值k·(t-200)来模拟漂移故障，并利用标准化欧式距离指标研究漂移故障特征，结果如图12、图13所示。

图12 漂移故障下相关挠度测点数据Fig.12 Data of relevant deflection measuring points under drift fault

图13 基于标准化欧距离的漂移故障检测结果Fig.13 Drift fault detection results based on standardized Euclidean distance

由图12可知，在t=200以后，测点2-2的挠度监测数据发生线性漂移，2组关联测点数据之间开始出现明显差异。由图13可知，在故障发生前，即t=1～200时，监测数据标准欧式距离值维持在故障诊断阈值之内，表征该阶段传感器监测数据间相关性强，挠度传感器并未发生故障。故障发生后，监测数据标准欧式距离值从t=200后开始较正常值发生漂移，并超出故障诊断阈值，可判定挠度传感器数据异常。综上分析，以标准欧式距离为指标能够初步检测出漂移故障，并能判定漂移故障时间。

为进一步研究不同的漂移程度对故障检测和定位稳定性，选取漂移速率k=0.02～0.05，常偏差值取值间隔为0.01，一共4组模拟试验进行分析，结果如图14、图15所示。

图14 不同漂移速率下的漂移故障检测结果对比Fig.14 Comparison of drift fault detection results under different drift rates

图15 不同漂移速率下的漂移故障时间定位结果Fig.15 Drift fault time location results under different drift rates

对比分析图14、图15中4组不同漂移速率的漂移故障模拟试验结果发现，漂移速率介于0.02～0.05之间时，均能准确诊断漂移故障，但漂移故障定位出现一定程度的固定后移，故障定位时间点t0=259，故障定位效率L0=70.5%。以上分析表明，标准化欧式距离指标在一定范围内基本能够检测出漂移故障，但故障时间定位后移，后移程度与故障诊断阈值的取值有关。