赵各庄矿矿井涌水量预测方法分析

赵志伟

（河北省煤田地质勘查院，河北 邢台 054000）

1 概况

矿井涌水量是指在矿山建设和生产过程中单位时间内流入矿井（包括各种巷道和开采系统） 的水量，是确定矿床水文地质条件复杂程度的重要指标之一，对矿井的经济技术评价有很大的影响，同时也是矿山设计部门确定排水设备和制定防治水措施的主要依据。矿井涌水量预计方法大致分为两类：第一类为确定性的数学模型法，其中具有代表性的方法为水均衡法、解析法、数值法；另一类为统计分析方法，如水文地质比拟法、涌水量降深曲线方程法、相关分析法、时间序列分析等。近年来也不断出现一些新的方法，尤其是随着计算机技术的快速发展，出现了许多智能型的方法，其中BP神经网络法是最具有代表性和革命性的方法。据统计，将勘探阶段预测的矿井涌水量与开采后矿井实际涌水量相比，误差小于30%的仅有10%，80%的矿区超过50%，有的甚至误差达到数十倍。造成矿井涌水量预测误差大的原因主要有水文地质条件未查清、选用的水文地质参数缺乏代表性和数学模型选择不当3 个方面。本文对赵各庄矿自1977 年以来历次矿井生产地质报告和水文地质报告采用的含水系数法、相关分析法、时间序列法、解析法、BP 神经网络法等矿井的涌水量预测方法合理性进行分析，以期达到为其它水文地质条件相似矿井涌水量预测方法选择提供依据的目的。

2 预测方法分析

2.1 地质背景

赵各庄矿位于河北省唐山市东北古冶区，开平煤田开平向斜之东北端。煤层集中分布于山西组（大苗庄组） 和太原组上段（赵各庄组），可采及局部可采煤层共7 层（5、7、9、11、12-1、12-2、12 煤层），第7、9、12-1、12-2、12 煤层为主采煤层。煤层倾角由缓倾斜区18°，发展到西翼急倾斜区的90°，直至反山区为倒转70°。受采掘破坏或影响的含水层为5 煤层至12 煤层砂岩裂隙承压含水层、12 煤层至14 煤层砂岩裂隙承压含水层、14 煤层至唐山石灰岩砂岩裂隙承压含水层以及奥灰岩溶含水层。

2.2 含水系数法

赵各庄矿1977 年的生产地质报告采用含水系数法对矿井涌水量进行了预测。含水系数法认为涌水量同产量有线性相关性。

通过对赵各庄矿1978—1982 年涌水量预测值与实测值进行统计分析（表1），误差均大于30%。该方法仅考虑原煤产量这一单一因素，未考虑开采方法、范围、进度等方面因素的影响，故采用该方法对涌水量进行预测精度较低，应用范围受到限制，但其原理简单，计算方便。有人提出将彼此独立的各影响因素变量综合成一个系统，考虑各影响因素的彼此干扰与涌水量的滞后响应等，在比拟法基础上建立应用范围更广的矿井涌水量预报模型[5]。

表1 原煤产量、涌水量预测值、实测值统计Table 1 Rawcoal production,water inflowpredicted value,measured value statistics

2.3 相关分析法

赵各庄矿1998 年的生产地质报告采用相关分析法对涌水量进行了预测[7]。报告中认为涌水量主要随开采深度变化而变化，同开采深度具有某种线性相关关系，建立了涌水量随开采深度的变化曲线，对各水平的涌水量峰值进行预测。

预测十一水平、十二水平、十三水平、十四水平正常涌水量峰值分别为2.72 m3/min、2.91 m3/min、3.10 m3/min、3.28 m3/min。赵各庄矿十一水平正常涌水量实测峰值为3.5 m3/min（2002 年），误差22%；十二水平正常涌水量实测峰值为4.64 m3/min（2013 年），误差37%；十三水平正常涌水量实测峰值为3.82 m3/min（2013 年），误差19%；十四水平涌水量还未达到峰值。误差在可接受的范围内。

相关分析法是一种统计分析方法，在计算过程中避开了那些难以确定的水文地质参数及一些未搞清的机理问题，通过分析因变量与自变量之间的关系，有助于人们了解问题的机理，从而有利于建立确定性预测。该方法的应用也有一定的限制，如各因素之间的相关关系比较复杂时，难以拟定回归方程。随着开采深度加大，各因素对涌水量的影响也会有所变化，难以形成可靠通用的计算式。由于不同矿区的充水影响因素不同，回归方程具有地域性，应用相关分析法时需要特别注意。

2.4 时间序列法

赵各庄矿2008 年生产地质报告[8]中预测十三水平涌水量采用的是时间序列法。

报告中对多年涌水量观测资料统计分析，认为矿井深部各水平涌水量随着开采强度的增加达到最大值，此后，随着下一个水平涌水量的增加，上一个水平涌水量逐渐衰减，而矿井总涌水量相对保持稳定。由于十三水平含水层的涌水高峰期已过，虽然由于降雨、断层和开采影响，涌水量也会有所变化，但属呈现稳定状态下的锯齿状跳动。取近10 a矿井正常涌水量的平均值2.61 m3/min 作为预测的矿井正常涌水量。

通过将2008—2012 年涌水量实测值与预测结果进行对比分析，预测结果误差均小于30%，见表2。分析认为，此方法对涌水量中长期变化规律性较强的矿井涌水量预测很有实效。

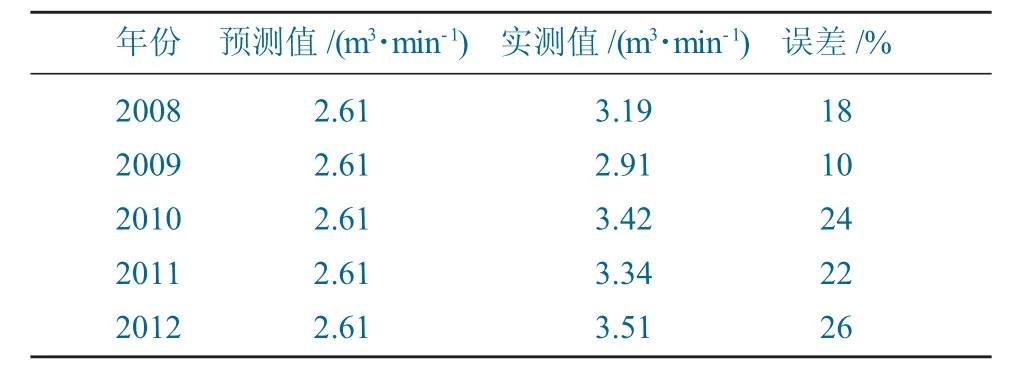
表2 十三水平正常涌水量预测值与实测值对比分析Table 2 Comparison and analysis of predicted and measured values of normal water inflowat thirteenth level

2.5 解析法

赵各庄矿2013 年水文地质类型划分报告采用解析法对十三水平涌水量进行了预测，采用承压转无压的完整井公式预计涌水量[9]。

预测十三水平正常涌水量为2.53 m3/min，而2013 年正常涌水量实测值3.82 m3/min，误差34%。导致误差偏大原因是裘布依涌水量方程的假设及简化条件是地下水为稳定流，可将空间流简化为平面流，且处于稳定流动状态。可是赵各庄矿地层倾角18°～90°，不能满足承压水顶底板呈水平分布的假设条件；报告中“大井法”预计十三水平矿坑涌水量时，计算水位降深百米以上，“大井”井壁水流早已不是缓变流，且由于不同富水性的多层含水层的复杂性，在大流量大降深条件下，很难处于稳定流状态。其物理模型已不符合裘布依涌水量方程的假设条件。

2.6 BP 神经网络法

赵各庄矿2014 年生产地质报告[11]采用BP 神经网络法对十三水平涌水量进行了预测。预测十三水平正常涌水量4.08 m3/min，2015 年实测值3.69 m3min，误差11%。基于主成分分析算法与BP 神经网络算法对于矿井涌水量预测具有一定的可行性，且精度较高，若原始数据集和网络结构良好，BP 神经网络算法可精确拟合结果[12]。

BP 神经网络方法预测涌水量适合于涌水量观测资料积累丰富的区域，恰好赵各庄矿积累了多年的涌水量资料，适宜该方法的应用。该方法充分考虑了开采面积、降水量、奥灰水位、开采深度和上水平开采面积等涌水量影响因素，得到的涌水量预测值是有一定参考价值的。

3 结论

（1） 相关分析法和时间序列法比较适合预计开采年代久远、有多年观测资料的矿井涌水量，如赵各庄矿。

（2） 含水系数法原理简单、计算方便，但是精度较低，该方法可以应用在预测新建矿井的涌水量，即利用地质和水文地质条件相似、开采条件基本相同的生产矿井的涌水量观测资料来预测新建矿井的涌水量。

（3） “大井法”一般适用于简化的勘探阶段或水文地质条件简单的情况，对于开采年代久远且地层倾角较大的赵各庄矿不适用。

（4） BP 神经网络法全面考虑了各种涌水量影响因素，具有相当好的应用前景。但对实际生产来说，充水水源和通道经常难以查清，需要时间序列资料的长期累积，并且一个神经网络系统往往只适用于某一特定的矿井，其他矿区则无法使用[13]。该方法有待于研究人员的进一步开发。