基于遗传神经网络的沥青路面抗滑性能预测及验证

2022-09-02张含伟苗超杰

公路交通技术 2022年4期

张含伟，苗超杰

(1.四川交投设计咨询研究院有限责任公司，成都 610041；2.重庆渝湘复线高速公路有限公司，重庆 401346)

沥青路面在使用过程中，受材料自身的限制、交通荷载的作用及环境因素的影响[1]，路表微观结构逐渐磨光、宏观构造逐渐降低[2-4]，路面抗滑性能不断衰减，严重影响道路行车安全，应及时采取有效措施恢复路表抗滑功能。为准确掌握路面抗滑修复时机，需对路面抗滑性能进行科学预测，以利于养护计划及方案的制定，从而实现路面使用的长期规划[5-6]。

沥青路面抗滑性能受诸多因素影响，一般的回归模型及马尔科夫模型只考虑时间序列参数的变化规律[7-8]，其模型结构较为简单，尚未考虑复杂环境因素等对路面抗滑性能的影响，预测精度受限。人工智能算法能够深度挖掘各因素与抗滑性能之间的关系，典型的BP神经网络模型[9-10]具有较强的自学能力和处理不确定因素等特点，能够建立复杂因素与路面抗滑性能间的高度非线性关系，更适用于路面抗滑性能预测。同时，遗传算法[11-12]具有全局搜索、适应性强、鲁棒性好等特点，能够很好地弥补神经网络局部最优、学习效率低的问题。为此，将遗传算法和神经网络模型有机地结合起来，建立遗传神经网络模型，以进一步提升路面抗滑性能预测的效果。目前以神经网络、遗传算法为典型的智能算法被广泛用于路面性能的评价及预测，单一的神经网络或遗传算法虽能建立抗滑性能与复杂因素间的高度非线性关系，但因算法自身的局限，预测结果存在局部最优、效率低下、精度不足等问题，而组合预测模型能够实现两者的优势互补，从而提高预测的可信度。

本文以重庆某高速公路Ⅰ、Ⅱ两段路面的抗滑性能预测为例，建立基于遗传神经网络的路面抗滑预测组合模型，计算遗传神经网络模型的预测精度、运算效率等，并与单一的神经网络、遗传算法及回归模型进行对比，验证该组合模型的适用性。

1 遗传神经网络模型

BP(Back-Propagation)神经网络模型是一种信息正向传播、误差反向传递的多层前馈网络模型[13-15]，其算法原理是：通过误差函数不断调节输入层、隐藏层及输出间的连接权值、阈值，使得预测值与实际值的误差满足精度要求。该模型具有较高的自适应性、较强的自学能力及泛化能力等优点，但也存在局部最优、收敛速度慢等不足。

遗传算法是一种并行随机搜索最优算法，其算法思想是“优胜劣汰”：对样本按照一定方式编码，通过适应度函数对每一代经过选择、交叉、变异的种群进行筛选，保留适应度好的个体，淘汰适应度差的个体，形成新的适应度更高的群体，直至满足群体最优。该算法具有多点搜索、全局搜索、收敛速度快等特点，能很好弥补BP神经网络模型的不足。

遗传神经网络模型是将两者优势结合起来，采用遗传算法对神经网络的解空间等进行优化，具体算法流程如图1所示，主要算法步骤如下：

图1 遗传神经网络模型Fig.1 Genetic neural network model

1) 数据归一化处理

不同样本数据间的量纲及数量级不同，影响神经网络训练效率及预测精度。采用MATLAB中mapminmax函数对样本数据做归一化处理。

2) 个体编码

编码方式是算法效率的关键，一般的二进制编码方式太长，影响算法效率。采用MATLAB编写code函数进行实数编码，编码长度为：

n=i*h+h*o+h+o

(1)

式中：n为编码长度；i为输入层个数；h为隐含层个数；o为输出层个数。

3) 适应度函数

每个个体解码后进行N次网络训练，以实际值与预测值均方差作为适应度函数。采用MATLAB编写fun函数对种群个体解码，并行性网络训练，计算适应度，公式如下：

f=k∑abs(yi-oi)2

(2)

式中：f为适应度；yi为i节点期望值；oi为i节点实际值；k为系数。

4) 选择操作

遗传算法一般采用轮盘赌的方式进行个体选择。采用MATLAB编写select函数选择优势个体，淘汰劣势个体，各个体选择概率公式如下：

pi=k/fi

(3)

qi=fi/∑fi

(4)

式中：fi为i节点的适应度；pi为被选中概率；qi为累计概率。

5) 交叉操作

采用MATLAB编写cross函数进行个体间实数交叉，其中第k个个体ak与第j个个体aj在位置i的实数交叉方式为：

aki=akj(1-b)+ajib

(5)

aji=aji(1-b)+akjb

(6)

式中：b为[0,1]间的随机数。

6) 变异操作

采用MATLAB编写mutation函数实现个体变异，其中第i个个体在第j个位置进行变异的方法如下：

aij=aii+(aij-amax)*f(g)r>0.5

(7)

aij=ajj+(amin-aij)*f(g)r≤0.5

(8)

式中：amax为aij上界限；amin为aij下界限；r为[0,1]间的随机数。

7) 网络微调

对遗传优化后的网络权值进行解码，并采用MATLAB自带神经网络工具箱函数对权值及阈值进行网络训练，达到设定预测精度。

2 建立路面抗滑性能预测模型

影响沥青路面抗滑性能的内因主要包括：原材料的种类及性质、沥青混合料的级配类型、沥青用量及施工工艺、质量控制，外因主要有：温度、雨雪、光照等环境影响、交通荷载作用、油气污染。对于在建高速公路，选择内因作为抗滑性能预测的输入因素较为合适，而对于营运高速公路，内因随时间的变化规律不易检测及调查，外因可通过查阅相关资料或现场调查获取，相对简单、直接，且外因的累加作用与路面抗滑性能衰变有很强的相关性，选择外因对营运路面抗滑性能进行预测更贴切。因此，本文选取使用年限、交通量、温度、降雨量及光照时长5个因素作为模型的输入参数，路面抗滑指标SRI作为模型的输出参数，建立基于遗传神经网络的路面抗滑预测模型，其网络拓扑结构如图2所示，具体模型参数设置如下：

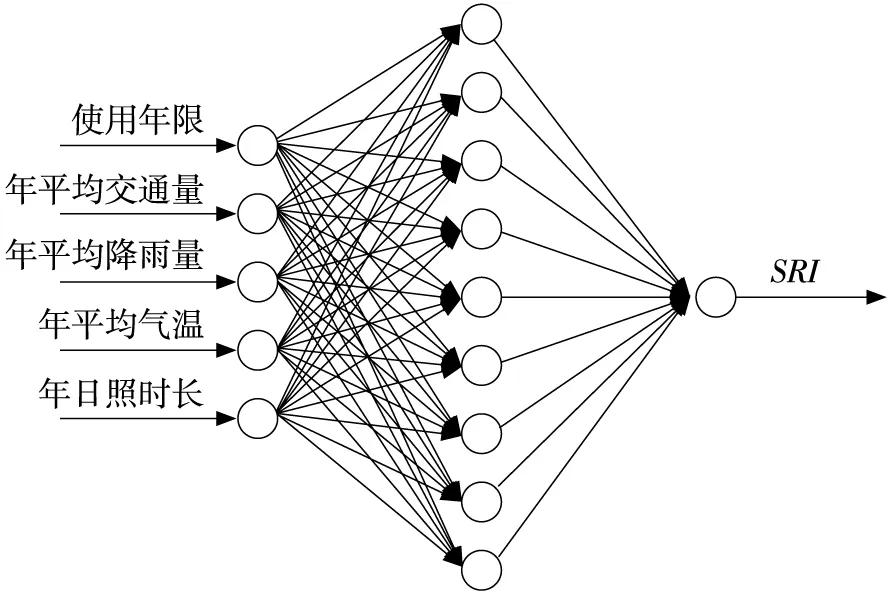
图2 神经网络模型结构Fig.2 Structure of neural network model

1) 网络目标精度：0.000 01；

2) 网络最大迭代：100；

3) 网络学习效率：0.1；

4) 种群规模：50；

5) 遗传代数：10。

3 工程实例验证

本文以重庆某营运高速为依托，选取不同使用年限、不同技术状况条件下的Ⅰ、Ⅱ两段路面抗滑指标SRI作为研究对象，收集并整理历年来Ⅰ、Ⅱ两段路的年平均交通量、年平均气温、年降雨量及年平均光照时长等数据，见表1、表2。

表1 Ⅰ路段路面抗滑影响因素统计Table 1 Influencing factor statistics of pavement anti-sliding in section I

表2 Ⅱ路段路面抗滑影响因素统计Table 2 Influencing factors statistic of pavement anti-sliding in section II

采用已建立的遗传神经网络模型对Ⅰ、Ⅱ两段路面的抗滑性能进行预测，其中以前5年样本值来训练网络，后2年数据进行模型检验，预测结果见表3、表4，残差结果如图3所示。

由图3残差分析可知：1) 整体残差数值，Ⅰ路段4种模型的抗滑预测精度均小于Ⅱ路段，即说明抗滑预测模型的精度与样本数据的质量有很大关系；2) 4种预测模型残差整体趋势，各模型均能很好地拟合样本，Ⅰ、Ⅱ两段路前5年的拟合精度不超过1%；3) 4种预测模型抗滑预测精度，Ⅰ、Ⅱ两段路均呈现回归模型预测精度最差，遗传算法、神经网络次之，遗传神经网络组合预测模型预测精度最高。结合表3、表4结果分析，预测模型的预测精度明显优于一般的回归模型，且相较回归模型，遗传算法预测精度平均提高1～2倍，神经网络平均提高2～3倍，组合预测模型则平均提高6～7倍，表明预测模型对于高度非线性拟合问题具有明显优势。另外，表3、表4表明，相较单一的遗传算法、神经网络模型，组合预测模型的预测精度显著提高，这充分验证了遗传神经网络组合模型是对单一预测模型的改进和优化，更适宜于路面抗滑性能预测。

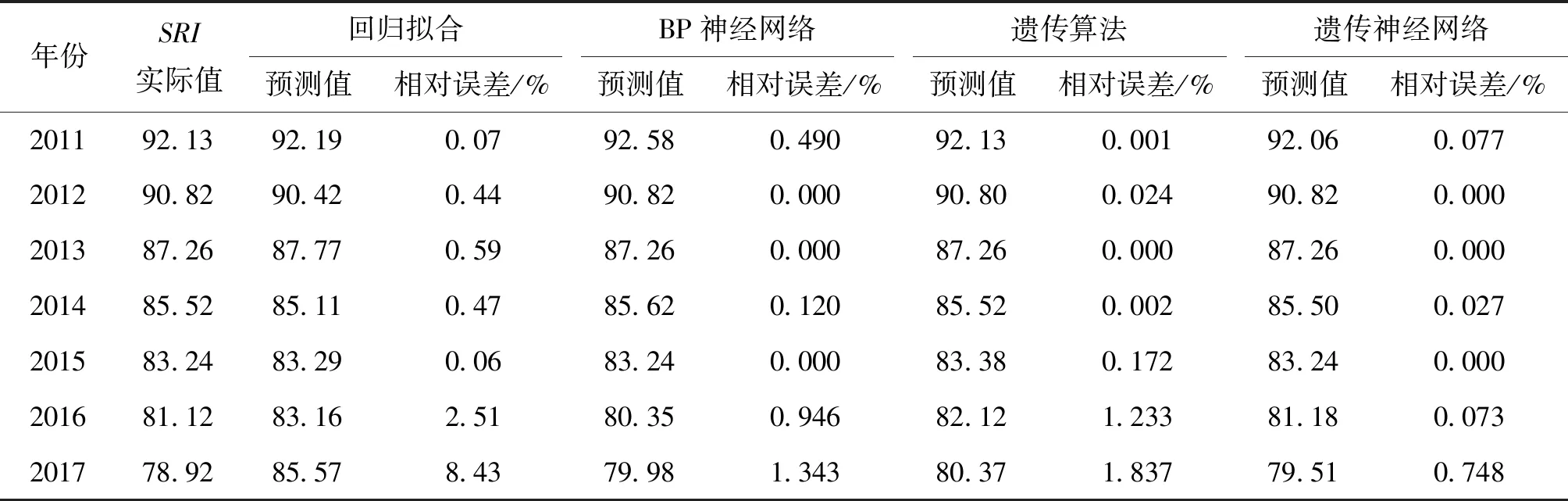
表3 Ⅰ路段路面抗滑性能拟合及预测结果Table 3 Fitting and prediction results of pavement anti-sliding performance in section Ⅰ

表4 Ⅱ路段路面抗滑性能拟合及预测结果Table 4 Fitting and prediction results of pavement anti-sliding performance in section Ⅱ

(a) Ⅰ路段4种预测模型相对残差对比

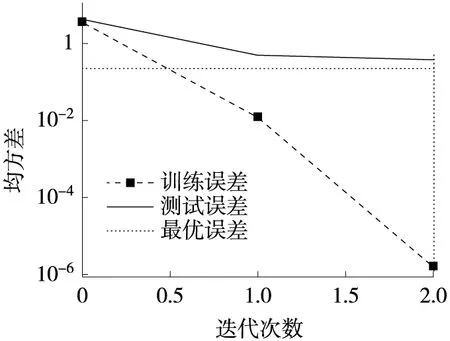
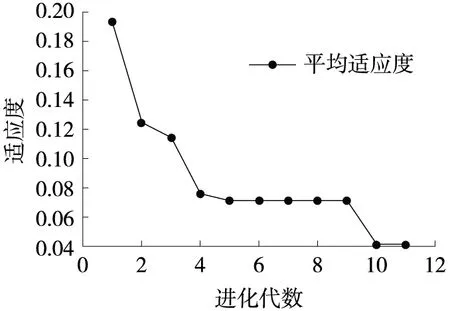
同时，为进一步验证遗传神经网络模型的优势及适用性，分别对3种预测模型的运行效率及迭代过程进行对比，具体运行效率对比见表5、表6，迭代过程如图4～图6所示。

表5 Ⅰ路段 3种预测模型运行效率对比Table 5 Operation efficiency of comparison three prediction models in section Ⅰ

表6 Ⅱ路段 3种预测模型运行效率对比Table 6 Operation efficiency of comparison three prediction models in section Ⅱ

(a) Ⅰ路段

分析表5、表6可知：1) Ⅰ、Ⅱ两段路，相同预测模型的运行效率相差不大，即预测模型的运算效率与样本大小相关；2) 在满足相同精度条件下，3种预测模型中，神经网络模型求解速度最快，遗传算法与组合预测模型速度相差不大，这是由于本文采用一般的遗传算法，多次通过随机方式进行选取、交叉及变异操作，影响了样本的进化速度。

结合图4～图6各算法迭代过程可知：遗传算法迭代过程变化较大，稳定性较差，神经网络模型及组合预测模型的迭代过程相对稳定。因此，从算法稳定性来看，采用遗传算法优化神经网络也是一种切实可行的组合方案。