让思维在沟联与拓展中走向深刻

谢锦璇

数学课程标准提出：“数学知识的教学，应注重学生对所学知识的理解，体会数学知识之间的关联。”教学中如何让学生在新课的学习上，能够自主地联系旧知识或相关知识来解决，使学生的数学学习更系统性，更有逻辑性？如何唤醒他们的记忆力，把一些关联的数学知识联结起来，感受数学知识的联系性？如何基于学生已有的知识经验进行有效的拓展和延伸呢？

一、 主动联结旧知，推进知识建构，激发思维

指向数学思维品质培养的数学课堂，一定要留足空间与时间，让学生主动思考，养成发现问题、提出问题、解决问题的能力。基于这样的思考，课前让学生提出他们想研究的问题，明确本课学习探究的目标与路径。让学生学会联系旧知，主动沟联，让知识深入浅出，让学习由浅入深。

(一)关联旧知，自主学习

片段一：教学《分数除法》时，老师可以这样提问：“今天我们一起学习分数除法，关于分数除法，你想知道什么？”学生可能回答：“分数除法的类型是什么？”“意义是什么？怎么算？”“为什么这样算？有什么用？”“与分数乘法有联系吗？”学生能够自如地提出这么多的问题，说明他们已养成联结旧知的习惯，能根据课题主动提出各种相关联的问题，提出教学目标与学习路径。学生迫切想明白为什么要学习这个分数除法，怎样学习，用什么方式来学习，怎样借助原有的知识解释新知识。

(二)对比沟联，融通知识

片段二：教学《猜数游戏》时，心里想一个数，把它乘2，再加上20，等于80？

师：怎样准确地猜到这个数呢？你有什么好办法？你是怎么想的？

生：用倒推法，根据一个数乘2再加20得到80，用80先减去20，再除以2。

师：你能用这单元学习的方程来解决吗？

生：把心里想的这个数设为，顺着这句话想的等量关系列出了方程：2+20=80。

接着引导尝试解决，此时坐立不安的学生自己发现了问题。

生：解方程每一步就是算术法。它们一一对应。

师：仔细对比这两个算式，你发现什么不同点和相同点？哪个地方一一对应呢？

生：解方程的第一步等式两边同时减去20和算术法(80-20)是对应的，第二步等式两边同时除以2和算术法60÷2也一一对应，结果一样。

生：第一个算式用倒推法来思考，用算术的方法来解决。第二个算式顺着题目的发展顺序来思考，用方程法来解决。

师：对，算术法是逆向思维，而方程法是顺向思维。

这样在教材的细节处进行对比沟联，推进知识建构，让学生的思维在对比中慢慢走向宽广。

(三)唤起联系，举例验证

片段三：教学《乘法分配律》时，从贴瓷砖主题图中抽象出两个等式：3×10+5×10和(3+5)×10，回头看看等式的两边为什么相等？大部分学生都能脱离情境联系乘法的意义进行解释，左边算的是3个10加5个10，右边算的是8个10。师：看来这个等式，不仅从结果上看是相等的，还可以从乘法的意义来验证左右两边是相等的。还能用其他办法解释这组等式是相等的吗？学生画点子图求总量、变长方形求面积、联想长方形周长、用生活事例来解释，此时老师对这几种验证方法进行沟联，归根结底，所有的解释都是联系乘法的意义3个10加5个10等于8个10，在数形结合中自主联系、沟通，快速地抓住问题的本质，凸显乘法分配律的意义。体会对某些数学知识可以从不同的角度加以分析，不同层次进行理解。也就是新旧知识间建立联系或产生矛盾，从而推进学生建构知识的进程。

二、 经常回顾反思，凸显数学本质，发展思维

课堂教学要基于对教材的深入解读，对学生学习路径的分析，顺应“从哪里来，是什么，到哪里去”。在不断回顾反思中引导学生用联系的眼光去发现与探究，找到知识的支撑点，准确理解、大胆说理、举一反三、意义建模，达到对知识系统的理解与灵活应用。

片段一：教学《百分数的认识》，作为“数”概念教学的核心，需要学生能描述其意义，并能结合生活实际进行解释。因此本堂课选取学生亲近的生活素材为主情境图，例如：男教师人数占全校教师人数的10%；果汁中含有50%苹果汁；食物中的蛋白质含量：牛奶3%、鸡蛋12%、豌豆25%。这3个素材从学生的生活中来，从学生已有学习经验出发，借助分数的率的意义来迁移学习百分数的意义。引导学生多角度解释百分数的意义后，第一次回过头看看这几个百分数有什么相同的地方，发现它们都是部分占整体的百分之几。接着在主情境图中“派哪名队员去罚点球？”让学生自主探索完，又引导第二次回头看看这两组分数与百分数的数据，有什么相同点与不同点？它们都是表示一个量是另一个量的百分之几，也是部分占整体的百分之几。在最后一个环节让学生解释生活中的百分数，又进行第三次回头看，找相同与不同。通过三次的回头看，找相同与不同，让学生在大量感知百分数具体意义的经验中多层建模，主动抽象出百分数都是表示一个数是另一数的百分之几，也就是表示两个数的关系，凸显百分数的本质。

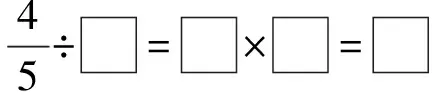
师：是不是分数除以任何整数的计算都是这样算呢？请举个例子说说。

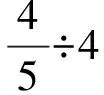
生：还可以更大的数，比如除以1000。

师：举得完吗？回头看，你想说什么？

生：除数不能为0。分数除以一个不为0的整数，相当于乘这个整数的倒数。

师：你真善于总结，能用一句话来概括分数除以整数的方法。除了用一句话概括，还可以用别的方式来概括。

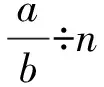
师：整数除以整数也是这样算吗？独立完成这道题。

师：回头看，你想到了什么？(横着看、竖着看)

生：整数除以一个整数(零除外)等于乘这个整数的倒数。

在多次回头的牵引下，不断地诱发学生进一步的猜想、联系、归纳，使思维不断向更深处、更严谨处延伸。

三、 借助已有经验，适度拓展延伸，提升思维

拓展和延伸是学生在学习原有知识的基础上，增加学生的知识积累，激发学生探求知识的愿望，培养创造性思维。因此，教师需要对教材进行适度的拓展和延伸，挖掘教材以外的相关资源的深层价值。

(一)多渠道地唤醒学生已有的知识经验，紧扣文本、适度拓展

课堂教学中经常创设开放性强、富有联想空间的问题，通过大胆猜想、联系生活，让知识延伸，让不同学生的思维得到不同发展。

片段一：教学《乘法分配律》时，关于乘法分配律，你能联想到什么呢？你有什么猜想？学生可能说：“加号可以变减号吗？”还可能说：“乘法分配律是否可用在减法中？(-)×=×-×。”也有的学生提出质疑：“乘号可以变除号吗？除法有分配律吗？(+)÷=÷+÷。”……这些猜想，都是学生对本课知识的拓展和延伸，对下节课的学习提出新猜想。这样富有生成性的教学，使学生思维的广阔性、独创性得到有效的培养。

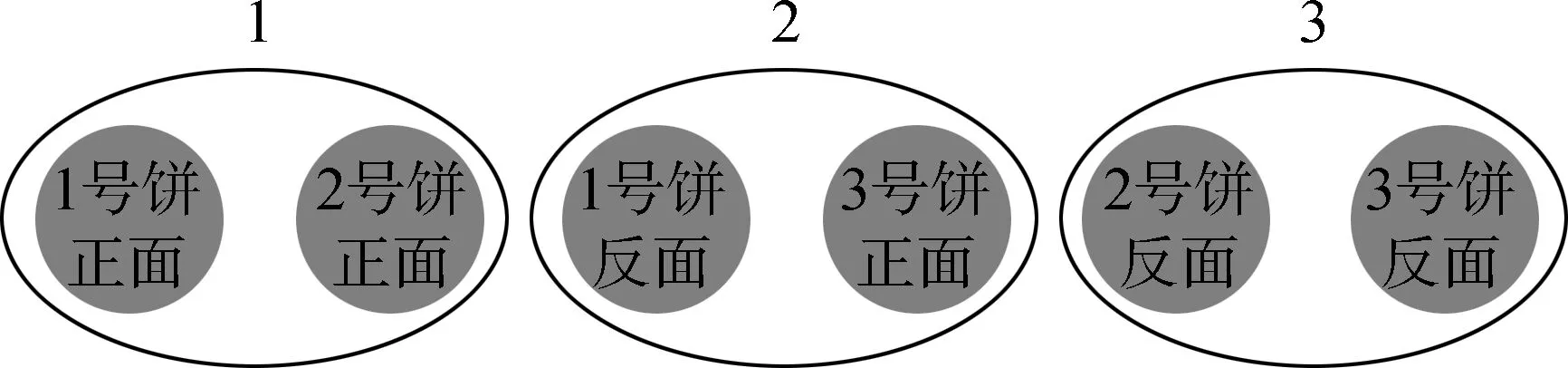
片段二：在教学《分数除法(一)》

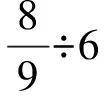
师：仔细阅读大家自己创编的实际问题，发现了什么共同点？什么变了、什么不变？

生：把一个数平均分成几份，求每份是多少？

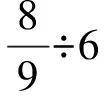
数学知识与现实生活密切联系，创设开放空间，让学生自主寻找模型的生活原型，帮助学生透过现象看本质，触摸数学拓展之魂。

(二)多层次地展现学生已有的知识经验，由浅入深、有效延伸

面对学生已有知识经验的差异，我们要精心布局，在关键深入的问题上发表意见，让不同层次的学生都有展示自己的机会；让知道一丁点儿的学生先说；知道多一点的学生后说；知道很多的学生最后说；知道浅一点的学生，让他在基本问题上发言；知道深一点的学生，让他进行补充，在互补中拓展与延伸，深度体验。

教学片段：在《烙饼》这一课的教学中，怎样才能尽快吃上饼呢？先让孩子用3个圆片(标上正反面)动手操作实践一下，实践完，分层次地说说想法。

知道一丁点儿的学生：我是一次烙一个面，一个一个地烙，6个面，每个面3分钟，所以18分钟。这类孩子就是因为没有读懂题目“每次只能烙两张”。

知道多一点的学生：两个饼同时烙正面3分钟，再同时烙反面3分钟，最后一个饼正面3分钟，反面3分钟，一共是12分钟。

教师引导：这类孩子没有考虑尽快吃上饼，就是烙饼时要节省时间，应该每次同时烙两个饼。

知道很多的学生：我用画图，每次锅里同时烙两个饼，1次3分钟，3次9分钟。

知道深一点的学生：一个饼有两个面，3个饼6个面，每次锅里同时烙两面，可以烙3次，共9分钟，可以直接计算3乘3等于9。

师：为什么呢？两个3分别表示什么？

生：第1个3是烙3次，另外一个3表示每次3分钟，共9分钟。

师：你怎么知道烙3个饼就是烙3次呢？

生：烙饼的次数=总面数除以2，所以3个饼就是烙3次。

师：烙饼问题的计算方法是最节省的时间=烙一面饼的时间乘烙饼的次数，照这样你能举一反三吗？烙10个饼几分钟？100个？1000个？

师：你能用一个简单的式子来表示吗？生：个饼就是3分钟。

这样分层的交流反馈，才能让不同的学生都有展示自己的机会，教师也可以知道孩子的知识在哪儿，思维障碍在哪里，助推新知由浅入深、由形象变为抽象，让不同学生的思维逐渐走向深刻。

(三)多形式地了解学生的已有知识经验，文化素养、拓深思维

教师可以设计课前问卷、问题调查，包括与教材紧密相关的知识生长点、延伸点等。使得在学习新课的前后有效地延伸文化内涵，发展学生的数学思维与文化素养。

教学片段：在《找质数》的课后练习教学时，在百数表中寻找质数，课前布置学生调查：“有关质数你想了解什么？知道了什么？质数有什么作用？”让学生搜集的资源发挥最大的价值，使学生在碰撞、对比、互补、互学中实现思维层面的提升。教学此练习题，先让学生独立完成题目并思考：“剩下的都是质数吗？”“这样排除够吗？”

生：还不够，划掉除7外所有7的倍数，剩下的才能都是质数。

生：我同意，49和77不是质数，其他数都重复排除，那么8、9的倍数也就不用排除了？

生：为什么呢？

生：是2的倍数也是8的倍数，是3的倍数也就是9的倍数。

师：大家已用筛选法，筛掉的数排列有什么规律吗？

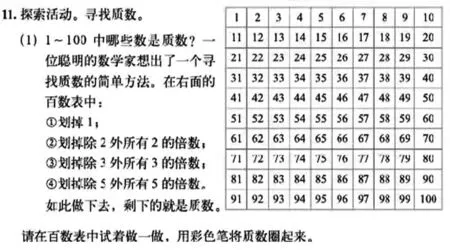
生：这些被划掉的数是2的倍数，分别在第2、4、6、8、10列。3的倍数成斜排，5的倍数在第5、10列。

师：这些排列你感受到了什么呢？生：我发现了这些合数，个位不变，十位变了。

生：其实这些都是合数，它们分别是2、5、3的倍数特征，它们的排列让我们感受到数学规律之美。

师：你们寻找质数的方法好像一个筛子，把合数筛去后，剩下的便是质数了，所以这种方法也成为“筛法”，是两千多年前希腊数学家埃拉斯特尼发明的，筛法文化让我们有序地找到质数，关于质数你有什么想问的吗？

生：为什么要找质数呢？

师：因为合数都能分成几个质数的乘积，所以质数被称为自然数的“数根”，任何一个大于1的整数，要么是质数，要么是合数。

生：质数在生活上又有什么作用呢？

师：用途很广，比如密码编码时加入质数，编码之后再传送给收信人，破解密码过程就是寻找质数的过程。

生：在汽车变速箱齿轮的设计上，齿轮齿数常设计成质数。

师：是呀，相邻的两个大、小齿轮齿数设计成质数，以增加两齿轮内两个相同的齿相遇，增强耐用度，减少故障。

生：杀虫剂使用在质数周期的时间上，实验表明，质数次地使用杀虫剂是最合理的。

师：质数次地使用杀虫剂都是使用在害虫繁殖的高潮期，害虫很难产生抗药性。

生：在军事设备上，导弹和鱼雷可以使敌人不易拦截。

师：那是导弹和鱼雷以质数形式、无规律变化的出现。

……

在练习讲解中之所以交流、碰撞出这么多有关质数的数学文化，都是来自学生在课外带着问题调查的结果，因为有提前让学生带着问题去调查，开阔数学眼界，使得本堂课的拓展水到渠成，丰富了对质数的认识，让学生用数学的眼光去看待生活，体会到生活中处处有数学，丰盈学生的数学文化素养。

每堂数学课，笔者总放慢教学速度，与学生行走在思考的路上，经常问问学生：“你感受到了什么呢？你有什么想问的吗？”师生之间的碰撞，才能促进学生之间的交流与补充，共同达到预期的教学目标。课堂中以学生的生活经验为主，在把握学情、深入解读文本的基础上进行适度、智慧的拓展延伸。让沟通联系真正发挥作用，让拓展延伸为深入理解教学内容而服务；让有深度的数学课堂植入学生的心田，使其思维得到绽放；让有趣的数学课堂慢下来，使其学习真正地发生。