考虑可执行度的地铁服务质量提升策略研究

2022-08-29陈维亚李嘉佳康梓轩

铁道科学与工程学报 2022年7期

陈维亚，李嘉佳，康梓轩

(1. 中南大学交通运输工程学院，湖南长沙 410075 2. 中南大学轨道交通大数据湖南省重点实验室，湖南长沙 410075)

根据我国交通部2019年公布施行的《城市轨道交通服务质量评价规范》[1]，城市轨道交通运营单位应当按照有关标准为乘客提供安全、可靠、便捷、高效和经济的服务，保证服务质量，采用先进技术提升服务品质；城市轨道交通运营主管部门应当通过乘客满意度调查等多种形式，定期对运营单位服务质量进行监督和考评。因此，运营单位根据运营服务质量评价结果制定合理的策略以提升服务质量，是地铁运营管理的重要工作。在根据指标评价结果制定服务质量提升策略时，由于受到技术条件和资源等限制，地铁运营单位往往难以在一段时期内同时提升所有指标，因此需要决策指标的改进优先级和改进幅度。重要性战略矩阵(Ⅰmportance-Performance Analysis，ⅠPA)是目前常用的决策方法[2]，其同时考虑指标的服务质量得分和权重，把指标划分为优先改进区、保持优势区、次要改进区和锦上添花区4个类别，对应4 种改进优先级[3]。但ⅠPA 的决策过程如未考虑指标改进的可执行度，则决策结果难以实施，效果难以保障。例如，张慧慧等[4-5]通过ⅠPA发现车厢拥挤状况是北京地铁和广州地铁优先改进区的指标。但是，北京地铁和广州地铁的客流量巨大，列车发车频率已基本达到极限，因此在一定时期内难以通过调整发车频率等运营管理手段增大运输能力和降低拥挤度。BAN等[6]通过模糊C-均值聚类算法改进了ⅠPA 中划分指标改进类别的方法，但ⅠPA决策不考虑指标改进可执行度的问题仍然没有解决。为此，本文在ⅠPA 决策模型中引入决策树(Decision Tree,DT)，构建DT-ⅠPA决策模型，实现融合考量指标的得分、权重和可执行度，决策出合理的服务质量提升策略，并以长沙地铁为例开展实证研究。

1 决策模型构建

1.1 模型框架

本文的决策问题是：根据地铁服务质量指标体系及评价得分，融合考量各指标的权重及改进可执行度，确定指标的改进优先级和改进幅度，以实现预期的总体服务质量提升目标。构建如图1所示的DT-ⅠPA 模型，输入数据包括指标体系和指标得分。决策过程分5 步：第1 步，利用指标体系和指标得分确定最佳决策树模型；第2步，基于最佳决策树计算指标权重；第3步，利用指标的权重和得分均值构建ⅠPA；第4 步，通过层次分析法(Analytic Hierarchy Process，AHP)量化改进指标的可执行度；第5 步，针对落在ⅠPA 优先改进区且无改进可执行度的指标，利用决策树中包含相关指标的分类规则，调整分类规则内指标的改进优先级并确定改进幅度，使调整后总体服务质量得分能达到较高等级。最后，DT-ⅠPA 模型将输出指标的改进优先级和改进幅度。以下详细阐述DT-ⅠPA模型的决策步骤。

图1 DT-ⅠPA模型框架Fig.1 Framework of DT-ⅠPA model

1.2 关键步骤

1.2.1 最佳决策树建立

决策树是由一系列的节点分裂而成的树状分类或回归模型。按节点分裂方法分类，建立决策树的算法分为ⅠD3，C4.5 和CART 等。由于CART的生成速度和分类准确率优于ⅠD3 和C4.5[7]，本文选用CART算法，由该算法构建的决策树模型为二叉树，即树的每个节点最多有2个子节点[8]。另外，因为地铁乘客服务质量的测评数据是离散的，所以运用CART算法建立的决策树为分类树，输入数据Ω 是各指标得分和总体服务质量得分，如式(1)所示：

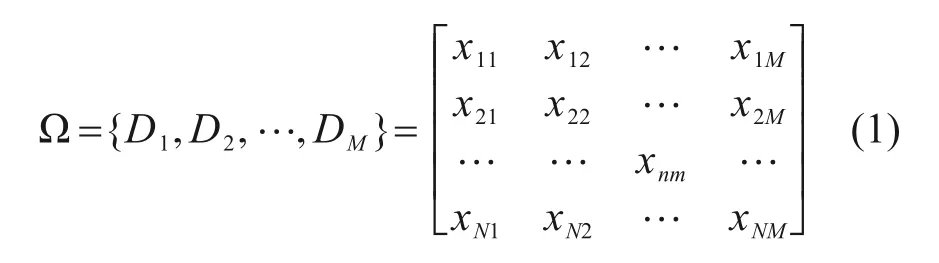
式中：行变量为被访者，列变量为服务质量指标；xnm表示被访者n对指标m的打分，n=1,2,…,N，N∈N*，m=1,2,…,M,M∈N*；Dm为指标m得分集合，Dm={x1m,x2m,…,xNm}。获得输入数据后，通过图2所示4个步骤建立最佳决策树。

图2 最佳决策树生成的基本步骤Fig.2 Basic steps for building an optimal decision tree

第1步，将数据集划分为训练集和测试集，为建立决策树模型并评估其分类准确率做准备。采用的方法是k折交叉验证，该方法具有确保来自原始数据集的每条数据都有机会出现在训练集和测试集中的优点。其中，k表示数据集划分后数据子集的数量，k-1组为训练集数据，用于生成饱和树。剩余的一组为测试集数据，用于测试剪枝树的分类准确度。数据集将进行k次划分，重复以上操作。大量的实验证明当k=10 时，所建模型的分类准确度最好[9]，因此本文选k=10。

第2 步，通过CART 算法，使用训练集数据生成饱和树。CART 算法定义Gini系数为节点数据类别不一致的概率，如式(2)所示：

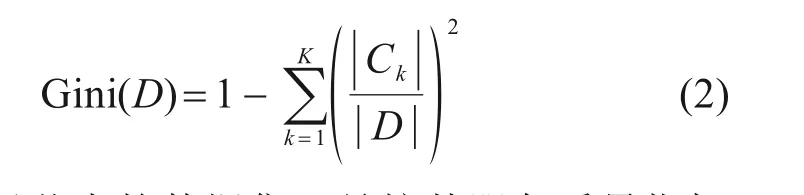
式中：D表示节点的数据集，是按某服务质量指标的某个得分划分的数据集，如“站内指引标志”得分大于2 的数据集；|D|表示数据集的数据量；k表示得分；|Ck|表示数据集D含有总体服务质量得分为k的数据量。

CART 算法分裂节点生成决策树的思想是最小化子节点的Gini 系数，即选择合适的分裂器使子节点的数据尽量属于同一个类别[7]。每一次分裂节点减小的Gini系数为：

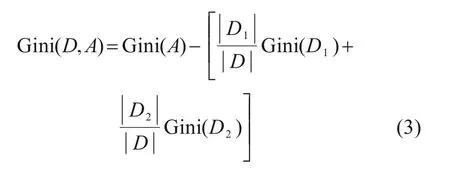
式中：A表示父节点的数据集；D1和D2分别为子节点1 和子节点2 的数据集；|D1|，|D2|和|D|依次为子节点1，子节点2 和2 个子节点数据集的数据量。

通过递归，决策树的Gini 系数会随着树的生长逐渐减小。当Gini 系数无法减小或叶子节点所含的数据量达到设置的最小值时，算法停止，获得饱和树[10]，记为T0。

第3步，利用代价复杂度算法剪枝，目的是避免决策树出现过拟合现象。代价复杂度剪枝的基本思想是用一个叶子节点代替饱和树内某个子树，生成一棵剪枝树。对这棵树进行相同的操作，递归，生成一系列的剪枝树T0,T1,T2,…,Tn。最后一棵生成的剪枝树Tn仅有一个根节点。

根据代价复杂度算法，令g(t)如式(4)所示：

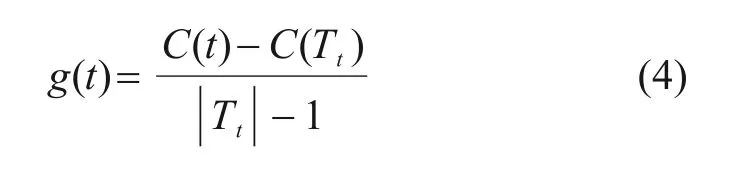
式中：|Tt|和C(Tt)分别是以节点t为根节点的树的叶子节点数量和预测误差；C(t)为剪枝后节点t的预测误差。

计算树Ti的每个非叶子节点t的g(t)值，找到令g(t)达到最小值对应的节点t，令t的左、右子节点为null，生成Ti+1。当多个非叶子节点的g(t)同时达到最小时，取|Tt|最大的节点t进行剪枝。

第4步，利用测试集数据从一系列剪枝后的决策树选出最佳决策树。定义所有叶子节点的Gini系数之和为决策树的分类误差率[11]，如式(5)所示：

式中：l表示叶子节点的编号；L表示叶子节点的数量；其余符号的含义与式(2)一致。

运用k折交叉验证划分的每个对折的测试集数据，计算T0,T1,T2,…,Tn中每棵决策树的分类误差率。因此，每棵决策树可获k个分类误差率，把k个分类误差率的平均值作为该树的分类误差率。一个简单的原则是选择交叉验证分类误差率最低的树。若简单的树和复杂的树的交叉验证分类误差大致相同，应优先选择简单的树，有利于使决策树避免过拟合。决策树的规模一般使用叶子节点数量表示[10]，叶子节点数量越多，决策树的规模越大。通过绘制剪枝树T0,T1,T2,…,Tn的分类误差率-叶子节点数量的图像，距离最小分类误差一个标准差的最小规模的剪枝树即为最佳树。

图3展现了基于式(1)，然后利用CART 算法构造的决策树的一般结构。它包含根节点、子节点、叶子节点和分裂器，节点用长方形表示，分裂器用菱形表示。根节点是所有指标的得分数据；总体服务质量指标以外的指标充当分裂器，按指标得分分裂；叶子节点代表总体服务质量的分类情况；其余节点表示其他指标的分类情况[10]。

图3 基于地铁服务质量指标得分数据建立的决策树一般结构Fig.3 General structure of decision tree based on score data of metro service quality attributes

1.2.2 指标权重计算

根据KASHANⅠ等[11]，指标权重是决策树的节点按该指标分裂后，节点Gini 系数减少的加权平均值(权重是分裂器所含样本量与所有数据样本量之比)。指标i的权重w(i)如式(6)所示：

式中：t表示以指标i为分裂器的节点，节点数量可能大于1；T表示决策树中所有节点的数量；nt表示以指标i为分裂器的节点的样本量；N表示根节点的样本量；D1和D2表示节点t以指标i为分裂器产生的子节点；|D1|，|D2|和|D|的含义与式(3)相同。

1.2.3 ⅠPA建立

以指标得分和权重为坐标轴，所有指标得分的均值和权重的均值为原点，建立如图4 所示的ⅠPA。基于所求的指标得分均值和权重，确定各个指标的初始改进优先级。

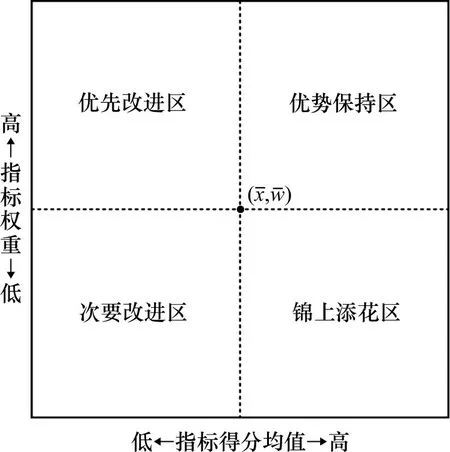
图4 重要性战略矩阵(ⅠPA)Fig.4 Ⅰmportance-Performance Analysis,ⅠPA

左上角象限为“优先改进区”，该区域的指标权重大于，得分均值低于，具有最高改进优先级，记为第1 优先级。右上角象限为“优势保持区”，该区域的指标得分均值和权重分别大于和，需要继续保持优势，具有第2 高改进优先级，记为第2 优先级。左下角象限为“次要改进区”，该区域的指标得分均值和权重分别低于和，具有第3 高改进优先级，记为第3 优先级。最后，右下角象限为“锦上添花区”，该区域的指标得分均值大于，而权重低于，具有最低改进优先级，记为第4优先级。

1.2.4 指标改进可执行度量化

指标改进可执行度是指在一定时期内考虑技术和资源等条件下，服务质量指标能够被改进的可行性及程度。本文利用层次分析法量化地铁服务质量指标改进可执行度。首先，请地铁运营管理专家通过1～9 标度法(见表1)两两比较指标的改进可执行度，根据比较结果构造判断矩阵。然后，计算判断矩阵的特征向量并检验一致性。若判断矩阵通过一致性检验，把归一化处理后的特征向量作为指标的改进可执行度；否则，对判断矩阵进行调整，直至通过一致性检验。

表1 指标改进可执行度1～9标度含义Table 1 The 9-point scale of the feasibility for attribute’s improvement

1.2.5 指标改进优先级和改进幅度确定

通过设计分类规则确定被调整指标的改进幅度，使总体服务质量得分能达到较高等级。从最佳决策树的根节点到每个叶子节点的路径为一条分类规则。

基于文献[10,12-13]，式(7)展现了一个分类规则例子，它可以解读为：当指标1 的得分均值≥k1，指标2的得分均值≤k2，到指标i得分均值＜ki，则总体服务质量有a%的概率得分为k。

决策树生成的分类规则并非全部有效，有效性一般使用Support(S)，Population(Po)和Probability(P)评价[10]。S 表示分类规则出现的概率；Po 表示分类规则中“如果…”部分出现的概率；P 表示符合叶子节点分类情况的数据量与该叶子节点所含的数据量之比。P等于S比Po的值，Po一般由P和S 计算。当分类规则的S，Po 和P 的值分别大于最小阈值时，分类规则才有效。如表2所示，不同文献给定的S，Po 和P 的最小阈值不一。若所设的最小阈值越大，则分类规则达标的难度越大，所得的评判结果更为可靠。文献[12-14]采用的S 最小阈值为0.006，处于中间位置，而P 为0.6，远大于其他文献，且考虑到该组的最小阈值应用更为广泛，因此本文采用该组阈值作为评判分类规则有效性的标准。

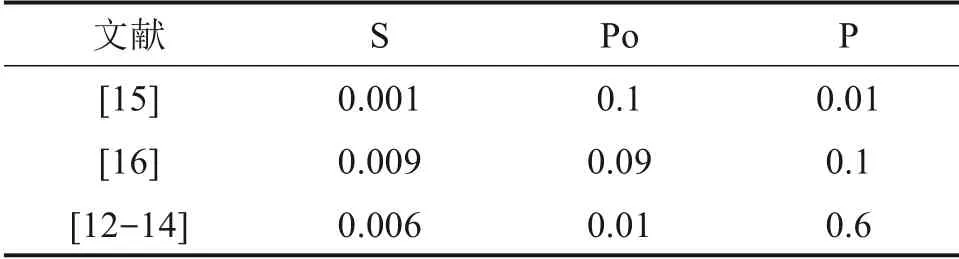
表2 决策树分类规则的S、Po和P最小阈值取值情况Table 2 S,Po,and P minimum threshold values of decision tree’s if-then rules

针对改进可执行度不足的指标，从决策树中提取包含相关指标且部分其他指标得分高于现状的分类规则。在分类规则的“如果…”部分，指标可划分为2类：改进可执行度不足的指标和改进可执行度足够的指标。对于改进可执行度足够的指标，根据指标当前得分是否达到分类规则所述要求，又可划分为达标和不达标2类。对于改进可执行度不足且得分已达标的指标，把它们的改进优先级调整为最低。而对于得分未达标的指标，把它们的改进优先级调整为最高，通过对照指标当前得分和分类规则所述得分要求确定改进幅度。不包含在分类规则的指标则不确定改进幅度。

2 实证研究设计与实施

2.1 问卷设计

本文通过乘客自填式问卷收集数据，问卷包含3 个部分。第1 部分，设置过滤问题“您是否曾经搭乘长沙地铁”筛选搭乘过长沙地铁的乘客。若被访者没有乘坐过长沙地铁，调查直接结束。第2部分，收集地铁服务质量指标得分。首先通过阅读文献[1, 17-21]，从安全、舒适和便捷3 个维度筛选出18 个指标，分别是车站可达性、站内指引标志、购票与充值服务、进出站闸机等候、线路图信息、扶手梯与升降梯、站内拥挤度、列车到站信息、候车时长、车厢拥挤度、噪声、照明、温度与通风、卫生、员工服务、生命与财产安全、运营时长和总体服务质量评价。各指标得分通过1～5分的五级数值量表测度，1分表示非常差的服务质量，5 分表示非常好的服务质量。第3 部分，收集被访者个人社会属性、出行特征和本次评价针对的运营服务时段信息，以了解样本的代表性和全面性。

2.2 调查实施与检验

调查于2020年11月在长沙轨道交通运营有限公司开展，采用自填式问卷向乘客调查长沙地铁2号线的运营服务质量，共收回130份问卷。剔除重复提交和存在漏答题项的问卷后，获得有效问卷107 份，大于所需最小样本量96(95%置信度，±10%误差)。

有效问卷被访者的个人特征、出行特征和评价的地铁运营时段统计情况如表3 所示。由表3 可知，被访者以男性为主，年龄段集中在20～40 岁之间，均拥有本科或专科以上学历。61.68%被访者每天都使用长沙地铁2 号线出行，29.91%被访者的使用频率为每周至少一次，说明大部分被访者对长沙地铁2号线的服务表现较为熟悉。绝大部分被访乘客使用长沙地铁的主要目的为通勤，占87.85%，其次为休闲娱乐，占10.28%。各个地铁运营时段都采集了评价数据，且评价高峰期的样本量比例大于平峰期，与客流分布特征相符。因此，各种特征的覆盖面较全且比例均匀，说明样本代表性较高。

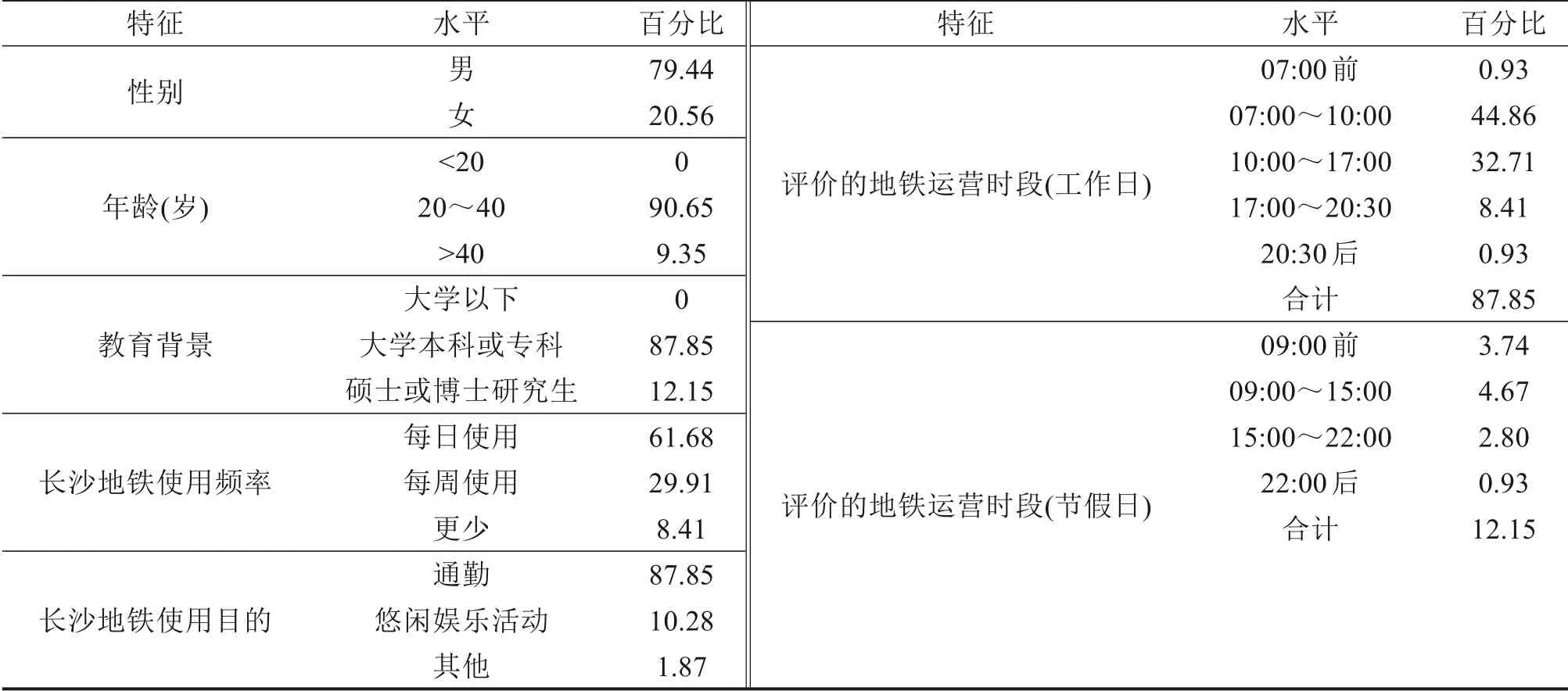
表3 有效问卷被访者信息统计Table 3 Statistics of respondents’ information from valid questionnaires

利用克朗巴哈α系数检验问卷信度，即检验测度结果的稳定性[22]。计算结果为0.964，大于DEVON 等[22-23]所述的阈值0.7，说明本次实证研究所获的数据结果具有良好的信度。

3 结果分析

3.1 最佳决策树

决策树通过MATLAB 2019b 建立，所得的一系列剪枝树的规模与分类误差关系如图5所示。可以发现，剪枝树对训练集数据的分类误差率随决策树规模的减少而单调递增，表明饱和树对训练集数据的拟合效果是最好的。另一方面，剪枝树的交叉验证分类误差随决策树规模的减少先减小，后迅速增加。当叶子节点数量为6时，相应的剪枝树是距离最小分类误差一个标准差范围内规模最小的树，因此被选为最佳决策树。

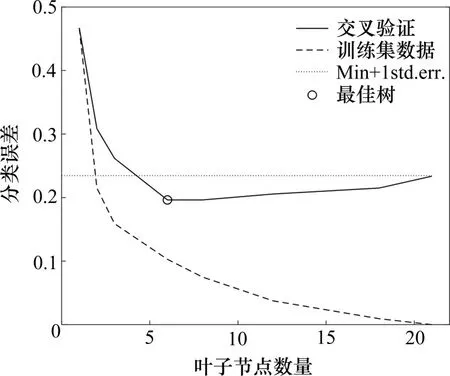
图5 剪枝树规模(叶子节点数量)与分类误差的关系曲线Fig.5 Relationship between the size of pruned tree(number of leaf nodes)and the misclassification error rate

最佳决策树如图6 所示，它有11 个节点，6 个叶子节点，深度为3，交叉验证分类误差为0.196 3，优于文献[24-25]的最佳决策树分类误差0.225 7 和0.211 3。

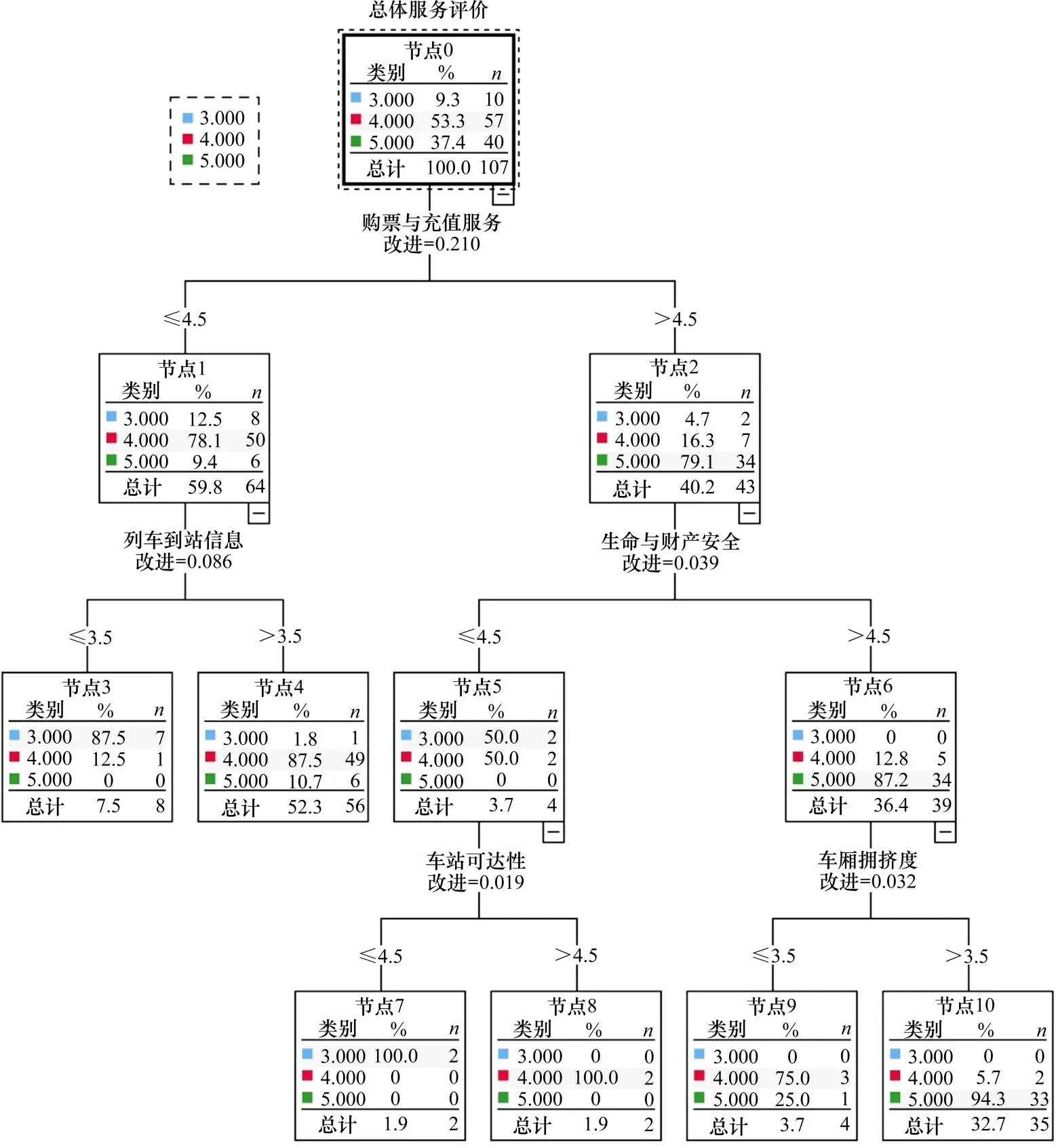
图6 最佳决策树Fig.6 Optimal decision tree

在图6中，每个长方形代表一个节点，呈现了节点中各个指标得分的样本量与所占比例。连接各个节点的路经径上的指标表示分裂器，下方的数字表示父节点分裂为子节点后，Gini 系数的下降值。

最佳决策树的根节点通过分裂器购票与充值服务分裂为节点1 和节点2，分裂的指标得分阈值为4.5 分。划分后，节点1 和节点2 的Gini 系数之和与根节点相比降低了0.210。节点1 表示购票与充值服务得分均值≤4.5分的数据集，节点2则表示购票与充值服务得分均值＞4.5 分的数据集。节点1和2 继续沿其他分裂器分裂，直至叶子节点3，4，7，8，9和10。

3.2 DT-IPA决策结果

利用实证研究所获数据建立的ⅠPA 如图7 所示，按1.2.3 所述方法可以确定各个指标的初始改进优先级。由图7可知，指标车厢拥挤度、站内拥挤度和购票与充值服务位于优先改进区，具有最高的改进优先级。根据1.2.4 所述方法求得这3 个指标的改进可执行度分别为0.06，0.19 和0.74，可以发现车厢拥挤度改进可执行度较差。从现实情况分析，购票与充值服务可以通过增设机器数量或者提高在线支付比例等方式提升效率，减少乘客购票与充值的等待时间，从而提升服务质量。站内拥挤度的服务质量可以通过限流进站提升。由于高峰运营时段列车的发车频率已接近饱和状态且列车的容量一定，车厢拥挤度难以通过增大发车频率等运营管理手段降低，增购车辆的成本则可能过高，因此改进车厢拥挤度服务质量的策略可执行度较差，于是把车厢拥挤度记作改进可执行度不足指标。

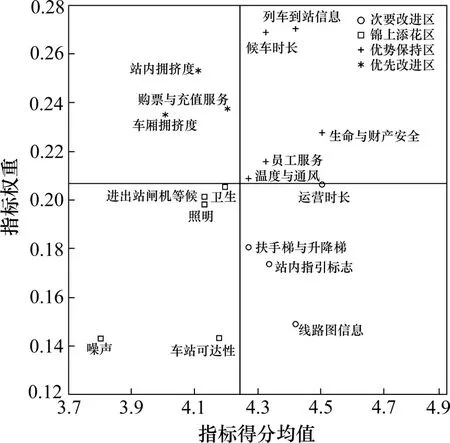
图7 ⅠPA决策结果Fig.7 Result of ⅠPA

表4 呈现了从最佳决策树中提取的6 条分类规则，它们均满足S，P 和Po 的最小阈值，是有效的。已知车厢拥挤度是改进可执行度不足的指标，根据1.2.5 所述方法，序号6 的分类规则可以用于调整由ⅠPA 确定的指标初始改进优先级，并量化被调整指标的改进幅度。

表4 最佳决策树包含的分类规则Table 4 Ⅰf-then rules from the optimal decision tree

6 号分类规则包含的指标为购票与充值服务、生命与财产安全和车厢拥挤度。由图7可知，生命与财产安全得分均值等于4.5 分，购票与充值服务得分均值低于4.5 分，二者均未满足6 号分类规则所述要求，服务质量需要提升。根据1.2.5 所述方法，购票与充值服务和生命与财产安全的改进优先级调整为第1级别，车厢拥挤度的改进优先级则调整为第4级别。

购票与充值服务得分均值差0.29 分到达4.5分，而生命与财产安全得分均值若提高0.01 分即可大于4.5 分，从而满足6 号分类规则。基于6 号分类规则可以发现，即使不提升车厢拥挤度的服务质量，通过至少提高购票与充值服务0.29 分和生命与财产安全0.01 分，总体感知质量将有94.3%的概率达到满分。经DT-ⅠPA 模型决策的长沙地铁2号线的服务质量提升策略总结如表5。从中可知，属于DT-ⅠPA 模型第1 改进优先级的指标的改进可执行度高于ⅠPA 的决策结果，反映了DT-ⅠPA 模型的有效性。