基于多日需求情景的高铁列车开行方案鲁棒优化
2022-08-29周文梁康静李莎黄裕
周文梁,康静,李莎,黄裕
(中南大学 交通运输工程学院,湖南 长沙 410075)
高铁列车开行方案确定了给定高铁线网上开行列车数量以及各列车开行径路、编组、停站与开行时段等,其编制密切依赖于高铁出行需求。“按流开车”是设计列车开行方案的最主要原则,既有研究通常针对单个运营日固定需求、弹性需求等优化列车开行方案。PARK 等[1-2]基于客流预测的固定需求值,兼顾铁路企业和旅客利益建立列车开行方案的多目标优化模型。史峰等[3]指出客运需求与旅客出行费用之间相互影响,弹性需求由固定需求波动而来,进而提出构造旅客运输弹性需求函数,以此需求优化列车开行方案。吕叶[4]通过“监测与预测相结合”的方法获取动态客流需求,提出基于动态客流调整列车开行方案的反馈模式。史峰等[5]针对一天内旅客需求在各时段的差异,在传统开行方案中引入列车始发时间,提出面向旅客服务水平的开行方案优化方法。在高铁实际运营组织中,不同运营日的出行需求在需求总量及其全天时空分布上均具有显著差异。目前铁路客运企业分别针对工作日、周末和节假日制定不同的列车开行方案,采用“日常线+周末线+高峰线”的模式。该方法适合于客流需求符合周期性波动的高铁线路,通常周内是出行平峰,周末是出行高峰,并且各运营日出行需求的时空分布也很相似。然而存在不少高铁线路,其客流需求不符合这种严格规律性变化。因此,非常有必要面向需要实施同一方案的多个运营日的出行需求优化列车开行方案。近年来不少学者研究列车开行方案鲁棒优化方法,核心思想是基于波动的客流需求找到不利情况下的最佳方案,即在所有可能情况下均可行且接近最优解的次优解,使得该开行方案实施于各运营日后,其经济性、服务水平不会很差。蒲松等[6-8]将客流需求限定于预测均值与峰值所构成的区间,以鲁棒性调节系数对需求变化的范围进行控制,构建可调鲁棒优化模型以解决因列车运能不足导致的“弃流”问题,从而协调开行方案的鲁棒性、经济性和服务水平。CACCHⅠANⅠ等[9]提出4 个鲁棒优化模型,其中之一是以未满足的客流需求最少为目标,以客流需求波动区间、列车总旅行时间和停站总次数的限制作约束条件构建模型。但这些研究主要验证了鲁棒性调节系数的变化越大,则客流波动范围越大,其对开行方案的影响就越大,并没有衡量得到的鲁棒优化方案是否接近各运营日的最优方案。本文将实施同一列车开行方案的每个运营日的实际需求视为一种需求情景,首先生成适应多需求情景的统一候选列车集,再以最小化最大后悔值[10](运营日实施的开行方案的目标值与该日最优方案目标值之差)为目标建立鲁棒优化模型,然后设计面向多个运营日差异化需求情景的模拟退火求解算法,得到能够同时有效适应各运营日出行需求的鲁棒优化方案。
1 问题分析和描述
考虑由N个车站构成的复线高铁线路,记下行方向车站依次为1,2,…,N。由于开行方案编制阶段高铁线路上、下行列车开行安排可视为相互独立,故本文仅研究下行方向列车开行方案。
1.1 需求情景集
将实施同一列车开行方案的每个运营日的出行总量及其时空分布描述为一种需求情景,所有需求情景构成本文研究面对的需求情景集,记为R。需求情景集R可以结合OD 客流预测与基于高铁售票数据的客流出行分布规律获得,即首先借助于历史售票数据分析拟合各OD 客流在不同运营日与全天不同时段的概率分布,进而将预测的各OD 需求量按此概率分布分散到各运营日以及各时段即可。因篇幅有限本文假定该需求情景集R已获得。
在任意需求情景r∈R内,每个OD 需求具有显著的时变特征。简便起见,将旅客全天出行时间范围划分为等时间长度,记M为需求时段总数,对于其中第m=1,2,…,M个时段,记和分别为其起始时刻与终止时刻。对于情景r∈R,记为起点i至终点i'的需求在时段m的出行量,其期望出发时间统一假定为时段m的中间时刻,即为。
1.2 适应多日需求的候选列车集
预先确定候选列车集不仅能确保开行列车更符合实际要求,而且有助于降低问题求解难度。针对单一需求情景,候选列车集的生成通常是先将不具备始发终到条件车站之间的客流归结到邻近具有始发终到条件车站,然后以具有始发终到条件的车站作为候选列车的起讫点,并依据车站始发终到能力、起讫点间客流分布、线路运输能力等限制大致确定候选列车数量及其开行路径与时间范围[11]。由于考虑多种具有差异性的需求情景,按各需求情景分别生成的候选列车集同样具有一定差别,为了使各需求情景实施同一列车开行方案,故需要生成统一的候选列车集。将每个需求情景对应的候选列车集按一定规则整合,既避免简单合并造成候选列车集规模激增,又能保证总候选列车集可以包括所有需求情景下旅客出行可选的列车。
记Lr为根据需求情景r生成的候选列车集,L={l=(Sl,El,ml)}为适应所有需求情景的总候选列车集,其中,l为一候选列车,Sl为候选列车l从始发站Ol至终到站Dl的途经车站集,El={ei,i+1=(i,i+1)|i,i+1 ∈Sl}为途经区间集,ml为候选列车l的始发时段。对于总候选列车集L与需求情景r对应候选列车集Lr,其所包含的时段m内从起点站o开往终到站d的候选列车数量分别记为建立两者关系如下:

其中,P为所有需求情景所产生候选列车的起讫点对集合。
在所有Lr的基础上,按式(1)关系确定总候选列车集L中各时段m,各起讫点(o,d)之间候选列车数量进而按此数量生成相应时段、相应起讫点对之间的多列候选列车,由此生成总候选列车集L。如图1 所示,假定A,B,D 和E 均为始发站或终到站,在时段m内起讫点为(A,E)的列车在3 个需求情景中的开行数量分别为3,5 和4 列,则在集合L中该候选列车开行数量为其中最大值5列;此外,虽然起讫点为(A,B)和(B,D)的列车只在情景1和情景3开行,但必须包含在集合L内。

图1 候选列车集生成示意图Fig.1 Diagram of a candidate-train-set generation
1.3 问题描述
本文研究问题可描述为:基于给定的高铁线路以及该线路多个运营日需求情景集,从所给候选列车中选择部分开行,并进一步优化列车停站和开行时间,在有效满足所有运营日出行客流服务的基础上,提高铁路企业的列车开行效益。
针对候选列车集L中每列候选列车,设置如下决策内容:
1)xl:候选列车l是否开行的0-1决策变量,若开行,则xl=1;否则,xl=0。
3):候选列车l在其始发站Ol∈Sl的发车时刻。
为简化开行方案优化问题的复杂性,运用以下假设条件:
1)假设各候选列车定员和速度等级相同;
2) 假设旅客选择直达目的地的列车,不考虑换乘情况。
2 模型构建
2.1 列车开行成本和旅客出行费用分析
列车开行成本主要包括组织成本和运行成本(与列车旅行时间成正比),可表示为:

其中,co为单位列车组织成本,元/列;cv为列车单位时间运行成本,元/min;为列车l在终到站Dl∈Sl的到达时刻。
为衡量开行方案适应各需求情景的程度,故需同时计算各情景下旅客出行费用,包括出发时间偏差(旅客期望出发时刻与所乘列车实际发车时刻之差)、旅行时间和票价,分别表示为:

利用旅客单位时间价值系数ψ将时间转化为与票价量纲相同的费用,则情景r∈R下旅客出行总费用表示为:
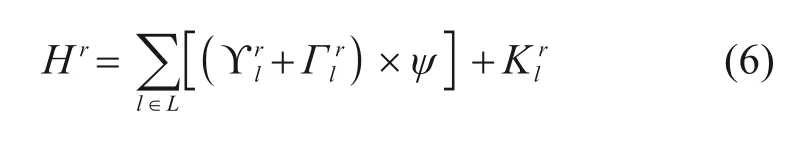
2.2 基于最小最大后悔值的鲁棒优化模型
通常每种需求情景对应一个最优开行方案,而在多需求情景下,鲁棒方案需要使开行列车与各需求情景的匹配性均较好。最小最大后悔值的思想来源于最小目标损失,即决策者从所选方案的成本与放弃的可能最低成本之间的差额最小的角度考虑制定决策[11]。本文用后悔值作为鲁棒解与最优解产生目标值的偏差,通过最小化最大后悔值(目标损失最大情况下的偏差)求解与各情景的最优解偏差最小的鲁棒解。
基于最小最大后悔值的鲁棒优化模型目标如下:

其中,Zr表示以需求情景r的客流分布优化开行方案产生的最优目标值;表示鲁棒解g*用于情景r得到的目标值,则为鲁棒解用于情景r时目标值与该情景下最优目标值的偏差,即鲁棒方案用于情景r的后悔值。
针对特定需求情景r,列车开行方案优化目标是最小化列车开行成本与旅客出行费用之和,即:

模型所需考虑的相关约束条件如下。
1)各时段的区间列车通过能力约束。
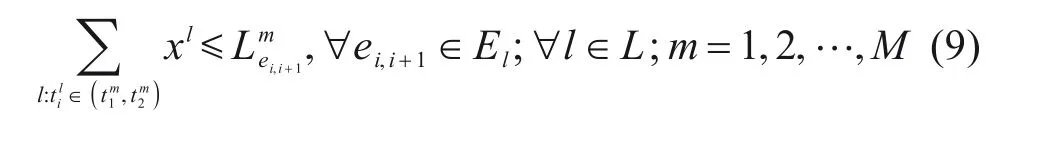
2)OD对服务水平的约束。

其中,l,l'∈L为在OD 客流起讫点(i,i')均停站的相邻2 列车,约束(10)限制这2 列车的时间间隔不能超过该时段允许的最大服务间隔ρm,即列车对各OD的服务必须保持在一定水平。
3)列车停站约束。
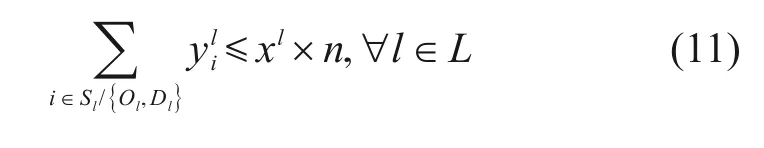
约束(11)确保任意列车l∈L在未开行时,其在中间车站均应不停车;若开行,其在中间停站不受限制。
4)客流约束。

其中,Cap为列车定员,人/列;为列车l在 运行 区 间ei,i+1上 的 载 客 量 ,=表示乘坐列车l的OD 客流是否经过运行区间ei,i+1,若经过,则=1,否则为0。
约束(12)确保各时段的OD 客流都会被分配到各列车上,使客流需求守恒。约束(13)和约束(14)保证分配至列车l的OD 客流量为非负数以及列车l在各运行区间的载客量不超出列车定员。
3 算法设计
考虑到模拟退火算法具有搜索新解能力较强、适用性较好等优势,被证实能有效求解列车开行方案优化问题[5],因此本节将结合模型特点设计模拟退火求解算法。
由于列车开行方案优化问题的复杂性,目前难以获得各需求情景下最优列车开行方案,一般只能获得近似最优解[13],亦称作各需求情景的满意解。显然采用各情景的满意解计算最大后悔值并不准确,为保证鲁棒解的优化质量,在求解过程中还需要结合鲁棒解的更新来改进各情景满意解。为此构建如图2所示的求解算法框架。
3.1 面向多需求情景的鲁棒邻域解搜索策略
首先同时分配各需求情景下的客流[14],在评估各开行列车服务质量的基础上,设计如下邻域解搜索策略并且按照调整列车开行数量、停站计划和始发时刻的顺序依次执行,以更新当前列车开行方案。
1) 增删开行列车
采用文献[15]中4.2 小节停开列车的策略,但不同的是本节计算各需求情景下各开行列车的平均客座率取各情景的平均值作为该列车客座率ηl;然后针对当前每列开行列车,计算其被停开的概 率其 中ηmax=为各列车中客座率最大值,进而按此概率采用轮盘赌方式选择列车予以停开,并释放相应的客流。
对于释放的OD 客流,首先考虑将其安排到同时段内具备可用能力的未停开列车上;对于无法安排的所有OD 客流,按其客流量以多到少的顺序,选择最合适的未开行候选列车并计算其平均客座率,若达到规定阈值则予以开行。任意增开的候选列车以其发车时段内最大时间空挡的中间时刻始发,按站站停方式生成停站。
2) 调整列车停站
运用文献[15]中4.2 小节取消和新增列车停站的策略,但不同的是本节计算每种需求情景下列车l在车站i的上下车客流量与在车站i相继停车的2 列车在该站的发车时间差值的乘积,然后取各情景下该乘积的平均值,再计算概率采用轮盘赌的方式调整停站。
3) 调整列车始发时刻
运用文献[15]中4.2 小节调整列车始发时刻的策略,但不同的是本节计算每种需求情景下乘坐各当前开行列车旅客的出发时间总偏差,然后取各情景下的平均值,再计算概率采用轮盘赌的方式调整始发时刻。
值得注意的是生成邻域解的方法并不是执行一个搜索策略就需要进行一次客流分配,因此改变策略执行顺序不会对优化结果产生影响。
3.2 模拟退火算法步骤
模拟退火计划表相关参数包括:初始温度Ψ0,温度下降比例θ,终止温度Ψend,恒温迭代上限Umax,最优解保持次数φ。算法终止条件为温度下降至终止温度Ψend或者最大后悔值在迭代φ次后无改变。
综上,形成面向多日需求情景的高铁列车开行方案鲁棒优化的模拟退火求解算法如下。
输入:高铁线路,候选列车集L,需求情景集R,模拟退火计划表参数。
输出:鲁棒解g*,最小最大后悔值F。
Step 1设置模拟退火计划表参数初始值,令当前温度Ψ=Ψ0,恒温迭代次数n=1。
Step 2首先应用文献[14]设计的针对单一需求的列车开行方案优化算法分别生成各需求情景r的初始满意解并设置各情景的当前满意解为=相应的目标值表示为Zr*。以各需求情景当前满意解分别作为鲁棒解,计算相应的最大后悔值,最后以最小的最大后悔值F(0)所对应的情景满意解作为鲁棒初始解g*(0),设置当前鲁棒解为并且令当前最大后悔值为=F(0)。
Step 3基于当前鲁棒解分别为各需求情景的OD 客流进行分配,以此为依据运用邻域解搜索策略产生鲁棒邻域解g(n)。
Step 4针对任意需求情景r∈R,若鲁棒邻域解g(n)使得Zr*>Zr(g(n)),则更新该需求情景满意解为并令Zr*=Zr(g(n));否则,保持原来满意解不变。
Step 5计算当前鲁棒邻域解g(n)的最大后悔值F′,并与当前最大后悔值比较,执行Metropolis准则:
2)若F′>且则接受鲁棒邻域解g(n)为当前鲁棒解且令
Step 6检验当前温度下迭代次数,若n=Umax,则降温退火,令Ψ=Ψ×θ,n=1;否则,令恒温迭代次数n=n+1,转Step 3。
Step 7若Ψ<Ψend或者当前最大后悔值在φ次迭代中未改变,则算法终止,输出最终的鲁棒解g*;否则,令n=1,转Step 3。
4 算例分析
本节以宁杭高铁线路为例检验模型和算法的求解效率和质量。宁杭高铁全长256 km,共设南京南站、江宁站、句容西站、溧水站、瓦屋山站、溧阳站、宜兴站、长兴站、湖州站、德清站和杭州东站共11 个车站。本文仅优化南京至杭州下行方向的列车开行方案,旅客全天的出行时间范围为06:00~23:00,以1 h 为时长,共划分为17 个时段。
考虑某周工作日5天的客流需求作为需求情景集,每天的出行需求总量分别为87 050,90 639,86 787,85 075,88 046 人次。各候选列车起讫点均为南京南站和杭州东站,其中出行高峰时段8:00~11:00 与14:00~16:00 候选列车均为8 列,其他时段为7列,全天共124列。
列车运营相关参数:列车运行速度300 km/h,列车定员1 053 人/列, 列车人公里票价率0.60元/(km·人)(按不同席别的座位数比例和客流出行距离比例计算得到),列车中间站停站时间3 min,列车单位组织成本4 000 元/列,列车单位时间运行成本150 元/min,旅客的单位时间价值系数37.8 元/h[16],服务于OD 对的列车最大时间间隔在出行高峰时段取45 min,其他时段取70 min。模拟退火算法相关参数:初始温度Ψ0=10 000 ℃,终止温度Ψend=100 ℃,降温速率θ=0.9,恒温迭代上限Umax=30,最优解保持次数φ=600。
算例求解采用MATLAB R2018a 编程实现。获得各情景初始满意解之后,最大后悔值收敛过程如图3所示,达到最优解保持次数后算法终止,曲线趋于平稳,证明该算法收敛性较好。

图3 最大后悔值收敛图Fig.3 Convergence diagram of maximum regret value
基于5 种需求情景得到的鲁棒优化方案如图4所示,其中包含列车的起讫点、开行数量、停站方案和开行时间等基本信息。共开行南京南至杭州东的列车61 列,包括直达列车9 列,站站停列车1 列以及择站停列车51 列。南京南站至杭州东站的客流需求相对于其他OD 对较多,因此需保证有一定数量的直达列车以提高这部分客流的出行效率。

图4 宁杭高铁下行方向列车开行方案Fig.4 Train plan of Ning-hang high-speed railway downward direction
为了分析鲁棒方案实施于各运营日的效果,考虑以下3种方案实施情形:其一,针对每个运营日需求独立生成实施列车开行方案,记为Sbest;其二,分别将基于每日需求获得的满意方案作为实施方案应用于所有运营日,分别记为S1,S2,…S5;其三,将本文获得鲁棒方案实施于所有运营日,记为Srobust。3 种方案实施情形对应的各项指标在5种情景中的平均值见表1。结果表明若从各需求情景的满意方案中选择一套开行方案实施于所有运营日,其总目标以及平均最大后悔值均大于本文所得鲁棒方案。相比情形S1,S2,…S5,情形Srobust下平均最大后悔值(5.073×104元)最小,与情形Sbest的总目标仅相差0.56%,这说明鲁棒方案能够比各需求情景独立优化产生的满意方案更能有效适应多日需求。

表1 3种方案实施情形关于各项指标的对比Table 1 Comparison of the indicators among the three implementation of the schemes
图5给出了鲁棒方案中各时段开行列车数与服务OD 客流量之间的匹配性。在8:00~11:00 和15:00~16:00 时段出行客流量最多,相应地开行列车数达到6 列左右;而在其余时段因客流相对较少,故列车开行3~4 列。由此可见开行列车数与客流需求随时间的变化趋势基本一致,这表明鲁棒方案能够使得各时段开行列车有效匹配各时段出行需求量。

图5 各时段开行列车数与服务OD客流量的匹配性Fig.5 Matching of the number of trains and the OD passenger flow in each period
图6 展示了各需求情景中各区间的运输能力、断面客流量和平均客座率的变化情况。运输高峰区间为溧水—宜兴区段,该区段的客座率在80%以上,大部分区间的客座率在70%左右,客座率最小值在50%左右,因此鲁棒方案中列车运输能力在各需求情景下均得到了较好的利用。

图6 各需求情景下各区间的运输能力、断面客流量和平均客座率Fig.6 Transportation capacity,cross-section passenger flow and average seat rate of each section under each demand scenario
5 结论
1) 本文考虑需要实施同一列车开行方案的多个运营日的差异化需求来优化开行方案,以最小化鲁棒方案与各需求情景的最优方案产生目标值的偏差为目标构建鲁棒优化模型,然后根据模型特点设计求解算法以改进鲁棒解。
2) 算例分析表明:鲁棒方案实施于各运营日与其实施各自满意方案相比,在总目标上仅相差0.56%,并且从各需求情景的满意方案中任意选择一个实施于所有运营日,其总目标均大于本文所得鲁棒方案,证明本文提出的列车开行方案鲁棒优化方法具有一定有效性和可行性。
3)没有考虑列车类别以及高铁线网中OD 对客流的换乘情况,所以研究仍存在一定不足,下一步工作不仅应着眼于此,还可以将列车开行方案与时刻表进行协同鲁棒优化。
