基于序贯辅助自适应渐消UKF的列车定位信息融合算法

2022-08-29李卫东余跃王运明初宪武

铁道科学与工程学报 2022年7期

李卫东，余跃，王运明，初宪武

(大连交通大学自动化与电气工程学院，辽宁大连 116028)

随着新一代高铁信号技术的不断创新与发展，新一代列车运行控制系统对列车精准定位提出了更高要求，使得传统的轨道电路、应答器等列车定位方式已不能满足下一代智能化列控系统的需求。我国建成的第三代北斗定位导航系统能够提供连续、高精度的定位服务，可为列车定位提供新技术[1]。因此，开展服务于下一代列控系统的列车精确定位技术研究具有重要理论意义和应用价值。为保障列车能够实时获取准确的位置信息，BDS 与ⅠNS 相结合的列车定位方式成为研究热点。BDS与ⅠNS的位置信息融合算法是提高定位精度的关键[2-3]，卡尔曼滤波算法作为信息融合的经典算法，已得到广泛研究[4-6]。然而卡尔曼滤波算法存在无法求解列车定位系统中非线性量测方程和获取精确先验统计噪声的问题。为此学者们提出了大量改进算法，AWⅠN[7]采用EKF 算法，将非线性方程直接线性化，但是当遇见高度非线性化系统时，效果极差。HU 等[8]采用标准UKF 算法，该算法对于线性化系统具有很高的适应性，但当遇到系统的模型和噪声不明确时，对于滤波发散现象的抑制不明显。LⅠU 等[9]将无迹变换与扩展卡尔曼滤波相结合，提出无迹扩展卡尔曼滤波(UEKF)算法，仍然存在滤波发散的问题。GU 等[10]提出了自适应UKF 算法，通过实时估计和修正系统噪声统计特性，并引入自适应渐消因子，提高导航系统的精度及可靠性。为有效提高BDS/ⅠNS 列车组合定位系统的精度，设计一种基于BDS/ⅠNS 的列车紧耦合组合定位系统模型，分别建立系统状态方程和量测方程，提出基于序贯辅助自适应渐消UKF 的列车定位信息融合算法。该算法在标准UKF 中引入自适应渐消因子，并采用序贯辅助方式，增加多重渐消因子的灵活度，降低滤波增益的计算难度，最后，仿真分析改进算法在卫星信号正常和部分卫星失锁情况下列车定位的有效性和精确性。

1 BDS/ⅠNS列车定位系统

列车定位系统主要是通过融合处理BDS 接收机、惯性导航器件(ⅠNS)等多传感器获取的位置信息，实现列车的精确定位。

1.1 BDS/INS列车紧耦合组合定位系统

根据列车定位信息的耦合程度，设计了基于BDS/ⅠNS 的列车紧耦合组合定位系统。列车紧耦合组合定位系统如图1所示。

图1 列车紧耦合组合定位系统Fig.1 Tightly coupled combined train positioning system

列车紧耦合组合定位系统分别利用北斗接收机获取实时广播星历中的卫星轨道参数以及由加速度计与陀螺仪等组成的ⅠNS 解算位置和速度信息，计算列车相对于卫星的伪距和差伪距，并将该值与BDS 接收机计算出的伪距和差伪距作比较后的结果作为量测值，使用自适应滤波器估计BDS与ⅠNS的误差量，并对误差进行反馈校正，从而实现列车的精确定位。

在列车紧耦合组合定位系统中BDS 接收机需要提供的信息包括广播星历以及伪距与差距率，当列车的BDS 接收机信号受到电磁干扰或山体遮挡，导致部分卫星信号失锁时，依然存在可用的BDS 信息，并且利用BDS 接收机给出伪距、伪距率与ⅠNS 计算出的伪距、伪距率进行组合[11]，提供列车一定时间内的定位与导航；并且该组合模式无需使用导航处理器解算列车的位置与速度，省去数据处理部分，具有精度高、鲁棒性好的特点。

1.2 列车定位数学模型

BDS/ⅠNS 列车紧耦合组合定位数学模型分为状态模型和观测模型2部分[12]。

1.2.1 系统状态模型

系统状态变量分为2 类[13]：ⅠNS 误差和BDS 误差。系统状态共描述为14维变量，表示为：

其中，前12 维为ⅠNS 误差，后2 维为BDS 误差，根据文献[14]可得出各部分的线性化误差模型。

结合ⅠNS 的误差状态方程和BDS 导航系统方程，建立列车定位系统的状态模型为：

简记为：

1.2.2 系统量测模型

列车紧耦合组合定位系统可用的量测据包括BDS 的伪距和差伪距率等测量值。观测矢量可以表示为ⅠNS估计值与BDS测量值之差，即

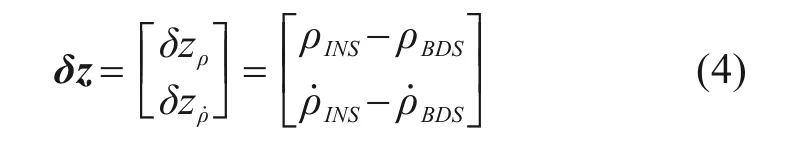
ⅠNS的伪距估计值为：

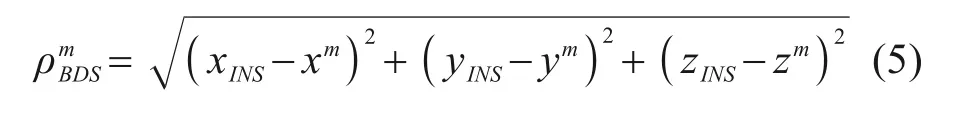
其中：(xINS,yINS,zINS) 为ⅠNS 输出的位置坐标，(xm,ym,zm)为第m颗卫星的位置坐标。

BDS的伪距可以表示为：

其中，(x,y,z)为当前时刻的位置坐标；δbr为接收机的时钟偏移误差；为其他噪声。然后，通过将ⅠNS 输出的位置进行泰勒展开，可以将伪距测量方程线性化，伪距方程在当前最优估计值(xINS,yINS,zINS)处线性化后可得：

进一步可计算出伪距测量误差模型，并经过坐标变化整理得：

其中

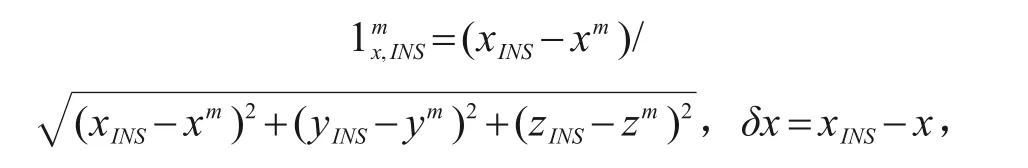
同理可得δy，δz和。

同理可得差伪距测量误差模型。

结合上述伪距误差和差伪距误差测量模型，并进行坐标变化，可得测量模型为：

式中：H(·)为非线性函数；V为量测模型的噪声。

2 基于序贯辅助自适应渐消UKF 的信息融合算法

将以上得出的列车紧耦合定位系统的状态模型和量测模型离散化处理，可表示为：

其中：wk-1为系统噪声向量；vk为量测噪声向量；wk-1与vk对应的均值与方差分别为qk-1，rk与Qk-1，Qk-1。

用卡尔曼滤波计算状态方程下一时刻的估计值和协方差矩阵：

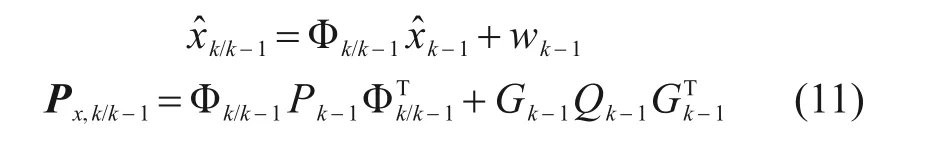
进一步，选取出2n+1个sigma点χj,k。

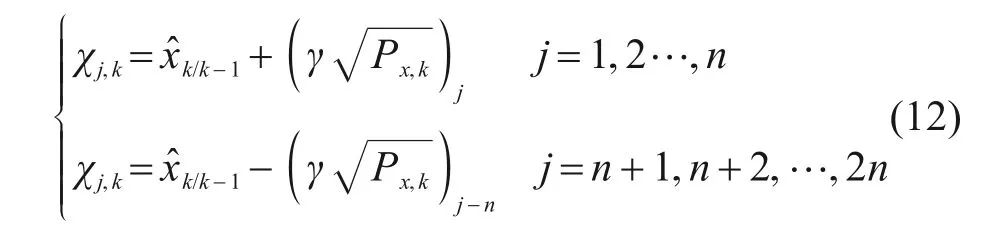
式中：χj,k的初值为n，α取0～1，κ=3-n。

将sigma 点代入量测方程进行量测更新，量测方程的系统参数表示为：

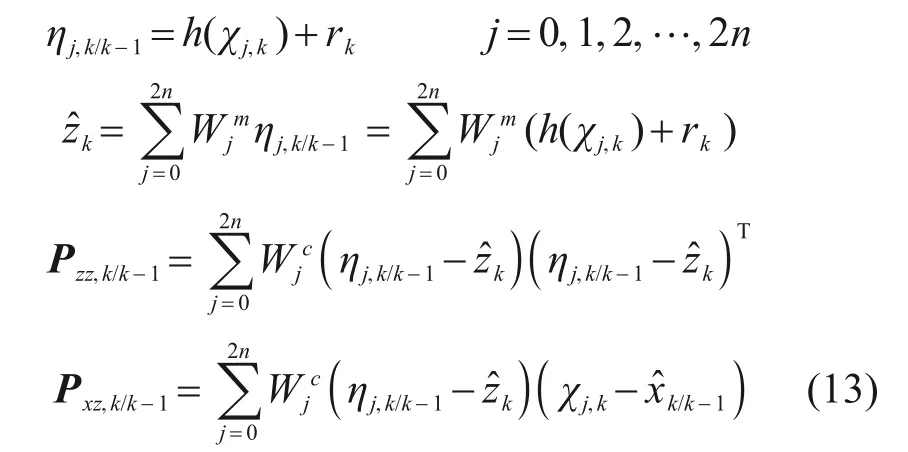
式中：ηj,k/k-1和分别为量测值及其均值；Pzz,k/k-1和Pxz,k/k-1分别为量测值协方差矩阵和互相关矩阵；和W c j为权值参数，计算公式为：

其中：β为常数，取值为2。

为防止列车高速运动时，量测噪声统计量随时间累计出现突变，引入渐消自适应因子加强近期数据的有效性，减少陈旧数据占比。量测均值的信息序列和协方差分别为：

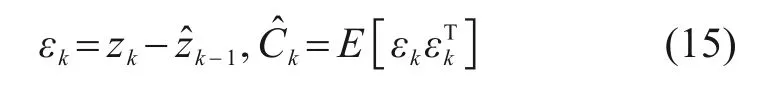
进一步，采用时间平均递推法将协方差Ck变形为：

其中，βk=βk-1/βk-1+b，b为渐消因子，β0=1,β0=1-b,0 ＜b＜1。将用于计算多重渐消因子Λk，可表示为：

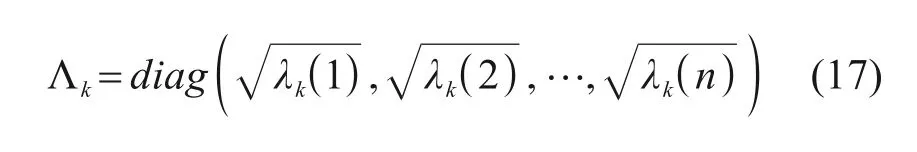
采用自适应一步算法得：

式中，αi为预设比例系数，αi≥1，Mk和Nk表示为：

式中：Φk/k-1与Hk分别为状态方程和量测方程的雅可比展开。下一步计算增益矩阵：

最后，更新量测方程，得出k时刻的滤波值和均方差估计，表示为：

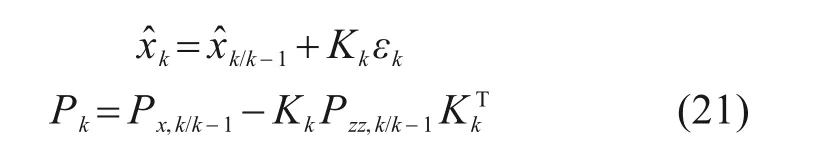
在自适应渐消UKF 算法中，引入多重渐消因子实质为平衡矩阵，通过自适应因子修正滤波中的异常值，减少前期数据对当前时刻的影响。为了提高多重渐消因子的灵活度，采用序贯辅助处理方法计算多重渐消因子，将多量测量的并行处理转换为串行处理。多重渐消因子序贯辅助处理公式如下：

采用序贯辅助处理后的增益矩阵表示为：

3 仿真验证与分析

为验证本文提出的序贯辅助的自适应渐消UKF 信息融合算法应用于列车紧耦合组合定位系统的有效性和准确性，采用以哈尔滨为起点的列车实测定位数据为样本，列车的初始经度和纬度分别为126.58°与45.71°；平均速度为99.90 km/h；最高时速为200 km/h；北向与东向初始速度分别为-204 m/s 与-42 m/s。设定北斗接收机采样时间为T=1 s，仿真时长为1 000 s。将标准UKF 算法与改进的UKF 算法应用于列车定位系统中，得出列车东向和北向位置误差曲线图如图2。

由图2 可以看出，采用标准UKF 算法的列车东向位置误差为6.1～-5.6 m，北向误差为6.2～-5.9 m；采用改进UKF 算法的列车东向位置误差为4.0～-3.7 m，北向误差为3.2～-3.7 m。

图2 列车位置误差Fig.2 Comparison of train positioning errors

将标准UKF 算法与改进的UKF 算法应用于列车紧耦合组合定位系统中，得出的列车东向和北向速度误差如图3 所示。由图3 可以看出，采用标准UKF 算法的列车东向速度误差为0.6～-0.6 m/s，北向速度误差为0.59～-0.55 m/s；采用改进UKF算法的列车东向速度误差为0.39～-0.35 m/s，北向速度误差为0.37～-0.35 m/s。

图3 列车速度误差Fig.3 Comparison of train velocity errors

以上误差数据可以看出，相较于标准UKF 算法，改进的UKF 算法的列车定位误差明显下降，说明改进UKF算法优于标准UKF算法。

为进一步验证改进算法的有效性，仿真分析卫星信号失锁情况下列车定位导航精度。仿真时长为500 s，设置在200～300 s 期间列车因天气或者山体原因，造成列车部分卫星信号失锁，该时段内有效卫星数为3 颗，列车其他参数保持不变，列车的误差计算结果如图4和图5所示。

由图4 可以看出，采用标准UKF 算法的列车东向位置误差在卫星失锁期间最大值为14.98 m，北向误差最大值为15.2 m；采用改进UKF 算法的列车东向位置误差最大值为8.8 m，北向误差最大值为7.92 m，表明改进算法在卫星信号失锁的情况下也具有较高的定位精度。

图4 卫星信号失锁时列车位置误差Fig.4 Comparison of train positioning errors

由图5 可以看出，采用标准UKF 算法的列车东向速度误差在卫星失锁期间最大绝对值为1.63 m/s，北向误差的最大绝对值为1.7 m/s；采用改进UKF 算法的列车东向速度误差的最大绝对值为0.797 m/s，北向误差的最大绝对值为0.855 m/s，改进算法较好地降低了列车定位的速度误差。

图5 卫星信号失锁时列车速度误差Fig.5 Comparison of train velocity errors

综上，在列车信号良好的情况下，相比于标准UKF 算法，改进UKF 算法的列车导航精度有了明显的提高；在列车卫星信号失锁的情况下，列车的导航精度有所下降，但是改进UKF 算法依然能够减少由于卫星信息减少所带来的影响，在100 s 的卫星失锁的时间内，依然能够提供10 m 以下的导航精度，达到列车定位的基本要求。