基于激活-熵的分层迭代剪枝策略的CNN模型压缩
2020-06-07陈程军毛莺池王绎超
陈程军,毛莺池,王绎超
(河海大学计算机与信息学院,南京211100)
(∗通信作者电子邮箱yingchimao@hhu.edu.cn)
0 引言
移动云计算作为移动互联网和云计算相结合的产物,利用云端的存储和计算等资源优势,突破移动设备的资源限制,提供卷积神经网络在移动终端部署的基础条件。AlexNet[1]、VGG-16[2]、GoogleNet[3-4]、ResNet-50[5]和 DenseNet[6]等新型卷积神经网络(Convolutional Neural Network,CNN)结构模型在相关领域内取得了较好的效果,但导致CNN模型朝层次增加方向发展,使大部分CNN模型都包含庞大的参数量,限制CNN模型在存储受限的移动设备上部署。移动设备(例如智能手机、医疗工具和物联网)几乎无处不在,对设备上深度学习服务的需求很高,包括对象识别、语言翻译、健康监控等,但目前大型深度学习模型因庞大的参数处理和存储受限,部署到移动系统仍然很困难[7]。有关研究证明大稀疏模型始终优于小密度模型,压缩大网络能取得比直接训练小网络更好的结果[8],因此模型压缩对于移动设备上部署CNN模型至关重要。
目前常用的模型压缩技术分为:剪枝、量化、网络分解、知识蒸馏和精细模型设计:剪枝包含基于正则化的剪枝[9]和基于重要性的剪枝,通过裁剪训练好的神经网络模型中冗余的权值或神经元,减少存储空间和加速计算;量化[10]使用位运算代替浮点运算,减少权重的比特数来压缩模型,加速模型计算;网络分解利用张量或矩阵分解技术分解原始卷积核,有效减少了运算量;知识蒸馏[11]借助大模型学习知识,指导小模型训练并代替原模型;精细模型设计重构了轻量级神经网络结构,如 MobileNets[12]、ShuffleNet[13]等,达到较好的压缩效果并显著提升运算速度,但设计模型时需要较高的技巧。
上述压缩方法中,模型剪枝策略灵活且容易实现,旨在深度神经网络的各种连接矩阵中引入稀疏性,从而减少模型中非零值参数的数量,而稀疏性参数被证明是权衡模型准确性及其内存使用情况的有效方法[8],具有较高的实用价值。本文采用模型剪枝策略解决CNN模型在移动设备上存储受限的问题。CNN模型在移动云环境中的部署架构如图1所示,整个系统分为三层架构,CNN模型的训练在云端进行,使用权重剪枝技术压缩训练好的模型,并将模型部署在移动设备和微云中。
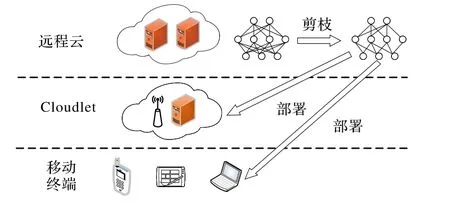
图1 移动云环境中CNN模型的部署架构Fig.1 Deployment architectureof CNNmodel in mobilecloud environment
针对CNN模型现有剪枝策略各尽不同和效果一般的问题,本文提出了一个基于激活-熵的分层迭代剪枝(Activation-Entropy based Layer-wise Iterative Pruning,AE-LIP)策略,保证模型精度在可控范围内的前提下有效缩减模型的参数量,使CNN模型在移动设备中的部署成为可能。本文所做的主要贡献如下:1)提出了基于激活-熵的权值重要性评判准则,计算权值在模型中的重要性得分,并裁剪重要性得分较低的权值;2)提出了面向层的迭代剪枝策略,使用试错实验法给每层单独设定剪枝率和剪枝迭代次数,并遵循筛选-剪枝-微调的步骤来压缩CNN模型。
1 相关工作
1.1 权值重要性评判准则
深度神经网络存在大量冗余参数,删除其中冗余的参数是一种有效的压缩手段[14]。模型剪枝的一般流程是通过分析权值或神经元的重要性,剪掉重要性低的权值或神经元,再进行模型微调。如何有效衡量权重对模型精度的影响是剪枝需解决的关键问题。基于Hessian矩阵的神经网络剪枝算法OBS(Optimal Brain Surgeon)[15],分析了权重变化对模型精度的影响,但计算Hessian矩阵的复杂度过高,使其在实际使用中受限制。基于幅度的剪枝方法使用权重的绝对值评判其重要性,绝对值越大的权重对模型精度的贡献越高并优先裁剪小权重[16],与其他剪枝方法相比,该方法简单且容易实现,但权重的大小难以反映权重在模型中的重要性,实验证明基于幅度的剪枝方法会误删一些重要的权值,导致模型精度在剪枝后大幅下降[17]。针对以上问题,学者们提出了其他评判准则,例如计算两个神经元激活值的相关性[18]、计算每个滤波器输出的熵值[19]、计算每个权值在下一层神经元激活值中的贡献度[20]等准则,作为衡量权值重要性的依据。
1.2 四类剪枝方法
根据剪枝粒度可分为连接级剪枝和神经元级剪枝,图2展示了两者区别。连接级剪枝又称为非结构化剪枝,以权重为单位进行裁剪,例如基于神经元相关性裁剪权重[18];神经元级剪枝又称为结构化剪枝,作用于单个神经元或滤波器,剪掉一个神经元相连的所有权重,例如根据几何中值对滤波器进行剪枝[21]。与神经元级剪枝相比,连接级剪枝具有更精细的裁剪粒度,对模型精度的影响较小。连接级剪枝会让原始网络变成稀疏网络,权重需使用稀疏矩阵存储,带来额外的存储开销,不利于缓存优化和内存访问,并且难以在通用硬件平台上加速。结合权重和卷积核的混合剪枝方法[22],将这两种粒度结合起来剪枝。

图2 连接级剪枝和神经元级剪枝的对比Fig.2 Comparison of connected pruningand neuronal pruning
根据剪枝是基于整个网络或单层可分为全局剪枝和逐层剪枝:全局剪枝在剪枝过程中分析模型的所有权重,筛选出一定数量的权重进行裁剪,例如逐步全局剪枝方法[24];逐层剪枝为网络中不同的层设置不同的剪枝比例,单独剪枝每一层。与全局剪枝相比,逐层剪枝考虑了模型中不同层的差异,对模型精度的影响较少,但确定每层的剪枝率是待解决的难题,处理过程较为繁琐。
根据剪枝过程是否迭代可分为单步剪枝和迭代剪枝。单步剪枝只进行一轮剪枝操作,剪枝完成后微调模型补偿精度损失,例如基于神经元连接灵敏度的单步剪枝策略[25],可以避免迭代剪枝的复杂性。单步剪枝可能一次剪掉大量参数,造成模型精度的大幅下降。迭代剪枝分为多轮,每一轮剪枝都会移除一定比例的权重并微调模型,通过多轮的剪枝-微调操作完成压缩。迭代剪枝对模型精度影响较小,但剪枝过程消耗时间更多。
根据剪枝后权重能否恢复可分为静态剪枝和动态剪枝。模型中各个神经元之间存在复杂的连接关系,将某些权值裁剪后可能导致其他权值的重要性发生变化,动态剪枝方法可以重新恢复被裁剪的权重[26]。
本文提出基于激活-熵的分层迭代剪枝策略,采用基于激活-熵的权值重要性评判准则,计算权值在模型中的重要性得分,裁剪得分低的权重。考虑模型精度的影响程度,采用影响较小的连接级剪枝;考虑模型中不同层的差异,采用试错实验法给每层单独设定剪枝率并逐层剪枝;考虑模型剪枝-微调后精度损失问题,采用迭代的方式进行多轮剪枝;考虑模型剪枝后神经元连接稀疏问题,采用静态剪枝并使用压缩稀疏行(Compressed Sparse Row,CSR)稀疏矩阵存储微调后的稀疏网络。
2 基于激活-熵的分层迭代剪枝
基于激活-熵的分层迭代剪枝策略主要分为基于激活-熵的权值重要性评判和面向层的迭代剪枝两部分内容,前者负责计算每个权值的重要性得分和按剪枝数量对权值排序,为后者剪枝和微调模型提供依据,最后用稀疏矩阵存储剪枝后的参数,节省存储空间。
许多研究[27-28]指出,大多数全连接层中存在大量冗余,因此本文主要修剪-微调全连接层。如图3所示,其中权重分布指当层所有权值在各取值区间的分布情况,它们近似服从高斯分布,在0附近区间内分布的小权重数远多于两端的大权重数,全连接层数量级远高于卷积层。
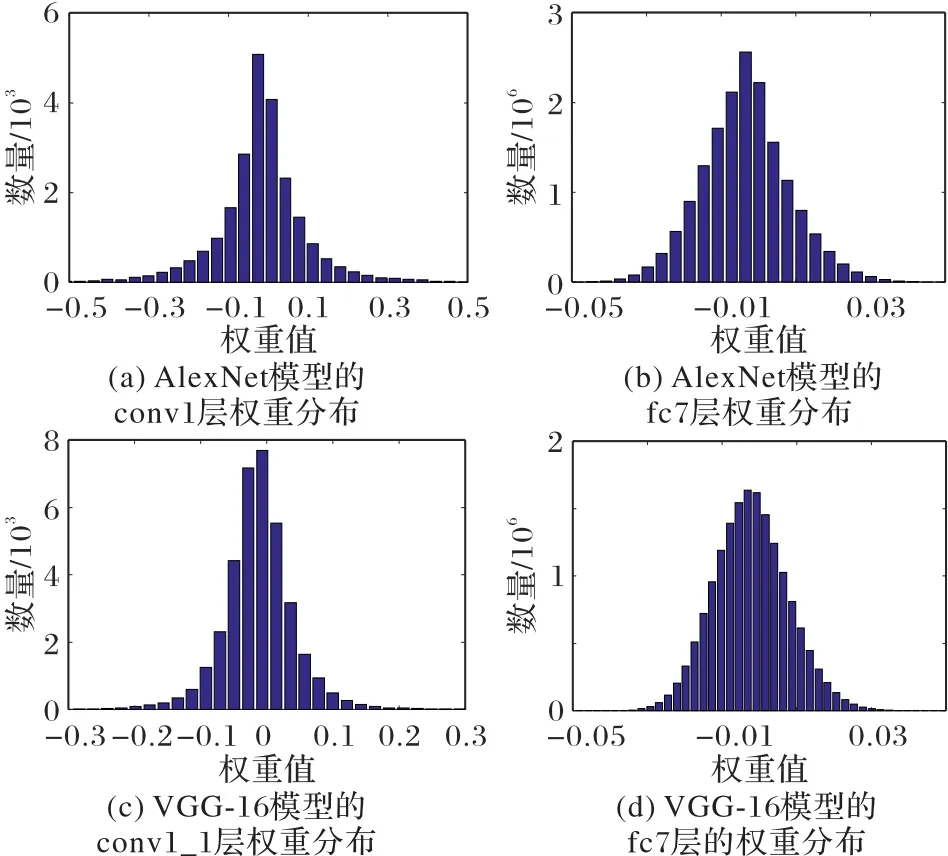
图3 AlexNet模型和VGG-16模型的权重分布情况Fig.3 Weight distributions of AlexNet model and VGG-16 model
2.1 基于激活-熵的权值重要性评判
给定神经网络模型C和训练集D={X={x0,x1,…,x N},Y={y0,y1,…,y N}},其中集合X和Y分别表示训练集中的输入和目标值。设神经网络权重集合为W=其中H为模型的总层数,Ci为第i层的权重数量。训练神经网络的目标是通过确定权重集合W,使模型在训练集D上的损失L(D|W)最小化。剪枝的目标是将原模型部分权重裁剪后保留M个权重得到新的权重集合W*,使剪枝后模型的精度损失最小[17]。剪枝可以转换为组合优化问题,通过搜索2|W|的解空间,获取剪枝的最优解,如式(1)和(2)所示:

由于CNN中权重数量庞大,采用遍历所有组合求出最优解的方式在实际应用中并不可行。目前大多数剪枝策略都是采用启发式方法评估权值重要性,优先裁剪不重要的权值,如基于激活的权值重要性评判准则[20],通过计算CNN模型在全连接层神经元激活值的期望,衡量权值的重要性。该准则证明了高度相关的对象对于深度架构中的后一层的活动具有更强的预测能力,通过计算神经元连接中的相关性,删除绝大部分较小相关性值,保留少量权重以补偿激活的变化。如图4所示全连接层的前向传播过程:i是上一层神经元的编号,j是当前层神经元的编号,上一层共有n个神经元,且神经元的输出为X。W j代表神经元j与上一层神经元连接的权重矩阵,w i为神经元i和j连接的权重值。设激活函数f(x)为线性整流函数(Rectified Linear Unit,ReLU),根据神经网络的前向传播公式,当f(W jTX)> 0时,神经元j的激活值如式(3)所示,其期望值如式(4)所示,对每一个权重w i,abs(E(w i x i))的值越大,则权重w i对下一层神经元激活值的贡献也越大,所以可通过神经元激活值期望的绝对值abs(E(w i x i)),衡量权值w i的重要性,即abs(E(w i x i))值越大,权值重要性越高。
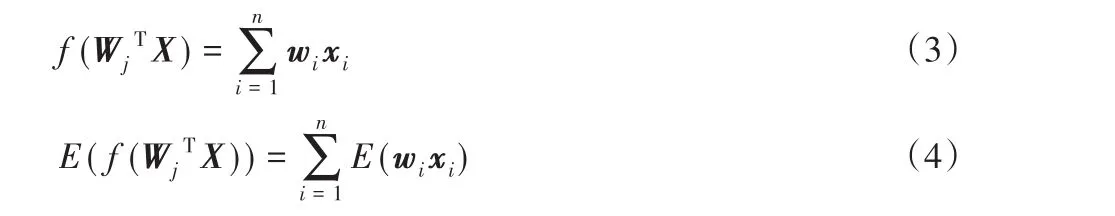
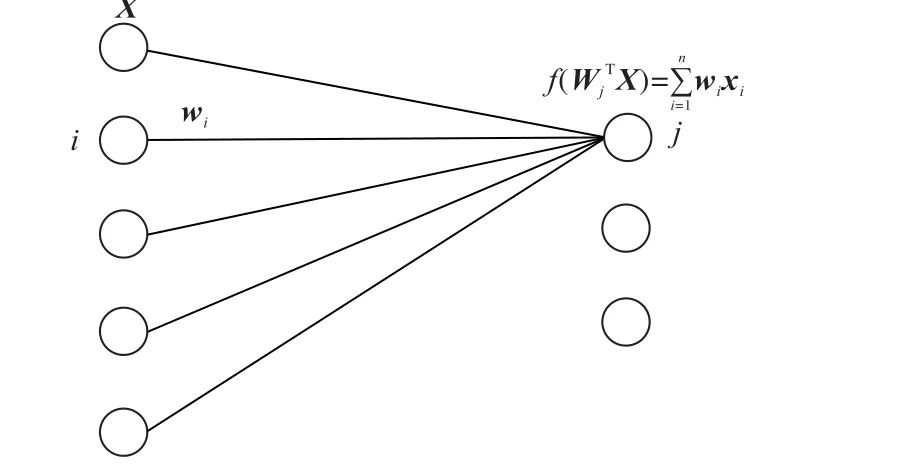
图4 全连接层的前向传播过程Fig.4 Forward propagation process of fully connected layers
许多启发式剪枝算法起源于计算相对熵最小化的近似,可以通过计算信息熵来衡量权值的重要性[19]。在信息论中信息熵越高,表明系统越混乱,不确定程度越高,能提供的信息量也越多,即剪枝策略中信息熵越小,其权值重要性越低[29]。w i x i的信息熵较小,则不同输入下w i x i的值集中分布在少数区间中,信息量较少,权重w i的重要性不高。设p(x i)为x i发生的概率,则离散变量X的信息熵值如式(5)所示。同理从训练集中随机选取K个样本,将w i x i的值划分为D个区间,使用pi,z表示w i x i的值分布在区间z中的概率,根据式(5)计算得到w i x i的信息熵Hi值如式(6)所示:

神经元激活值期望的绝对值abs(E(w i x i))越大,权值w i重要性越高,信息熵Hi越小,权值w i重要性越低,因此激活值和信息熵关于权重重要性都呈正相关。后文实验证明,激活值和信息熵相结合的基于激活-熵的权值重要性评判准则scorei,在保证精度的情况下,可以有效提高压缩率。scorei可以用来衡量权值的重要性,得分越高,则权值在模型中的重要性也越高,在剪枝时优先裁剪重要性得分较低的权值,如式(7)所示:

2.2 面向层的迭代剪枝策略
迭代剪枝对模型精度影响较小,配合剪枝策略,可以提升压缩精度。逐层迭代剪枝策略使用试错实验法测试不同剪枝率下模型的精度变化,根据精度变化趋势确定每一层合适的剪枝率。每层剪枝采用迭代方式,每一轮遵循筛选-剪枝-微调的步骤,避免一次剪掉大量权重造成模型精度大幅下降。设模型第m层共包含Nm个权重,且该层的剪枝率为pm,指定最大迭代次数Im,则每轮迭代需要剪掉的权重数量如式(8)所示:

本文提出的基于激活-熵的分层迭代剪枝策略(Activation-Entropy Based Layer-wise Iterative Pruning,AELIP)如下所示。
算法 AE-LIP策略。
输入 原始CNN模型E,待剪枝层1,2,…,n,待剪枝层的剪 枝 率p1,p2,…,pn,待 剪 枝 层 的 剪 枝 迭 次 数I1,I2,…,In,待剪枝层的权重矩阵W1,W2,…,W n。
输出 剪枝后的CNN模型E*。
for eachm=0 tondo //逐层进行剪枝
for eacht=0 toImdo //迭代进行剪枝
for eachi=0 toNmdo //权重矩阵W m中权值的总个数权值的重要性得分
end for
Δsm=pm NmIm//确定剪枝数量
index=Sort(scorei,Δsm)
//按重要性得分和剪枝数量对权值排序
Set(W m,index) //将筛选出的权重置为0
Retrain(E) //微调模型
end for
end for
returnE*//返回剪枝后的模型
面向层的迭代剪枝流程主要步骤如下:首先,使用数据集训练神经网络,得到原始CNN模型;然后,使用试错实验法确定待剪枝层的剪枝率,并设置每一层的剪枝迭代次数;最后,对待剪枝层逐层进行剪枝,每一层剪枝遵循筛选-剪枝-微调的步骤。从训练集中选取部分样本,根据式(7)计算每个权值的重要性得分,将权值按照重要性得分从小到大排序。然后根据式(8)计算需要每一轮需要裁剪的权重数量,并将筛选出的权重置为0。最后微调模型即重新训练网络,补偿剪枝后模型的精度损失,其中已被置为0的权重不会被更新。完成所有待剪枝层的剪枝操作后,则获得压缩后的CNN模型。
2.3 稀疏权重存储
模型剪枝后神经元之间的连接稀疏,通常采用稀疏矩阵存储剪枝后的权重。常用的稀疏矩阵包括CSR、压缩稀疏列(Compressed Sparse Column,CSC)、协调(COOrdinate,COO)、ELLPACK以及Hybrid等,其中CSR稀疏矩阵使用较为广泛[30]。如图5所示,CSR稀疏矩阵由非零元素、列索引和每行第一个非零元素索引三元组构成。设非零元素个数为b,行数为u,则CSR矩阵一共需要存储2b+u+1个元素。剪枝后模型的存储空间由两部分组成,包括非零权重所占用的存储空间以及稀疏矩阵所占用的存储空间,稀疏矩阵的存储开销降低了模型的压缩率。CSR矩阵可以在稀疏度高的网络中达到更高的压缩率[8],尽管存在额外的存储开销,与模型大小相近的稠密网络模型相比,稀疏网络模型的准确率更高,并且在大规模网络中表现尤为明显。
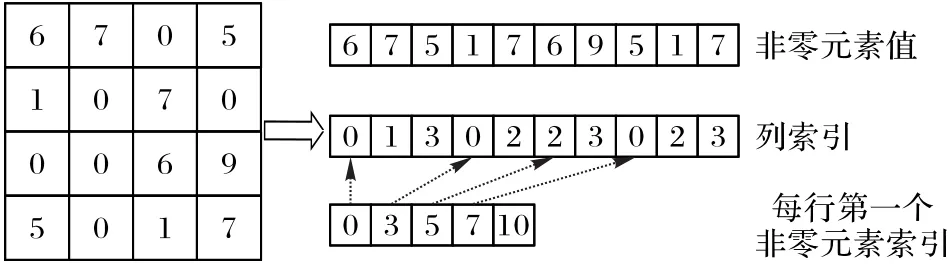
图5 CSR稀疏矩阵存储格式Fig.5 Storage format of CSRsparse matrix
3 实验验证
3.1 实验环境与数据集
本章实验使用Pytorch-1.0.0作为深度学习框架,实验环境如表1所示。

表1 实验环境Tab.1 Experimental environment
实验使用CIFAR-10数据集训练和测试卷积神经网络模型。CIFAR-10是深度学习领域常用的一种用于普适物体识别的数据集,共包含50 000张训练图片和10000张测试图片,图片共包含10个类别,每张图片都是大小为32×32的彩色图片[31]。本实验在CIFAR-10数据集上训练了AlexNet和VGG-16两种CNN模型。
AlexNet模型共有20层,其中8层含参数,包括5层卷积层 conv1、conv2、conv3、conv4、conv5以及 3层全连接层 fc6、fc7、fc8。训练好的AlexNet模型在测试集上的准确率为77.15%。
VGG-16模型共有38层,其中16层含参数,包括13层卷积层 conv1_1、conv1_2、conv2_1、conv2_2、conv3_1、conv3_2、conv3_3、conv4_1、conv4_2、conv4_3、conv5_1、conv5_2、conv5_3以及3层全连接层fc6、fc7、fc8。训练好的VGG-16模型在测试集上的准确率为89.63%。
3.2 实验结果与分析
3.2.1 单层剪枝实验
单层剪枝实验选取AlexNet和VGG-16模型部分全连接层,在不进行微调的情况下,逐步增大剪枝率,观察模型在测试集上准确率变化情况,其中微调可以有效补偿剪枝带来的精度损失,但对算法的优劣不产生影响。本实验通过选取基于幅度的权重剪枝[16](Magnitude)和基于相关性的权重剪枝[18](Correlation)策略与基于激活-熵的权重剪枝(Activation-Entropy)策略比较测试集上准确率变化情况,验证本文提出的激活-熵评判准则的有效性。
如图6所示,AlexNet和VGG-16模型由于全连接层中存在较多冗余权值,当剪枝率较低时模型精度无明显变化。对于AlexNet模型的fc7层,当剪枝率在50%以下时,使用三种策略剪枝后的模型精度仍保持在70%~77%;当剪枝率达到95%时,全连接层中剩余的权重数量较少,剪枝后模型的精度都出现大幅下降。基于激活-熵的剪枝策略的精度损失大概为23.5%,基于相关性的剪枝策略的精度损失约为25.5%,基于幅度的剪枝策略的精度损失达到了26.4%。在剪枝过程中,基于幅度的剪枝方法效果最差,基于激活-熵的剪枝方法由于保留了对下一层神经元激活值贡献较大的权重,精度损失相对较小。对于VGG-16模型的fc7层,基于幅度的剪枝方法在剪枝率达到90%时模型精度出现明显下降,剪枝率达到95%时精度只有57%左右,而基于激活-熵的剪枝策略的精度可以达到61%。综上所述,当剪枝率较低时AlexNet和VGG-16模型的精度几乎没有损失,而较高的剪枝率下基于激活-熵的权重剪枝效果较好。
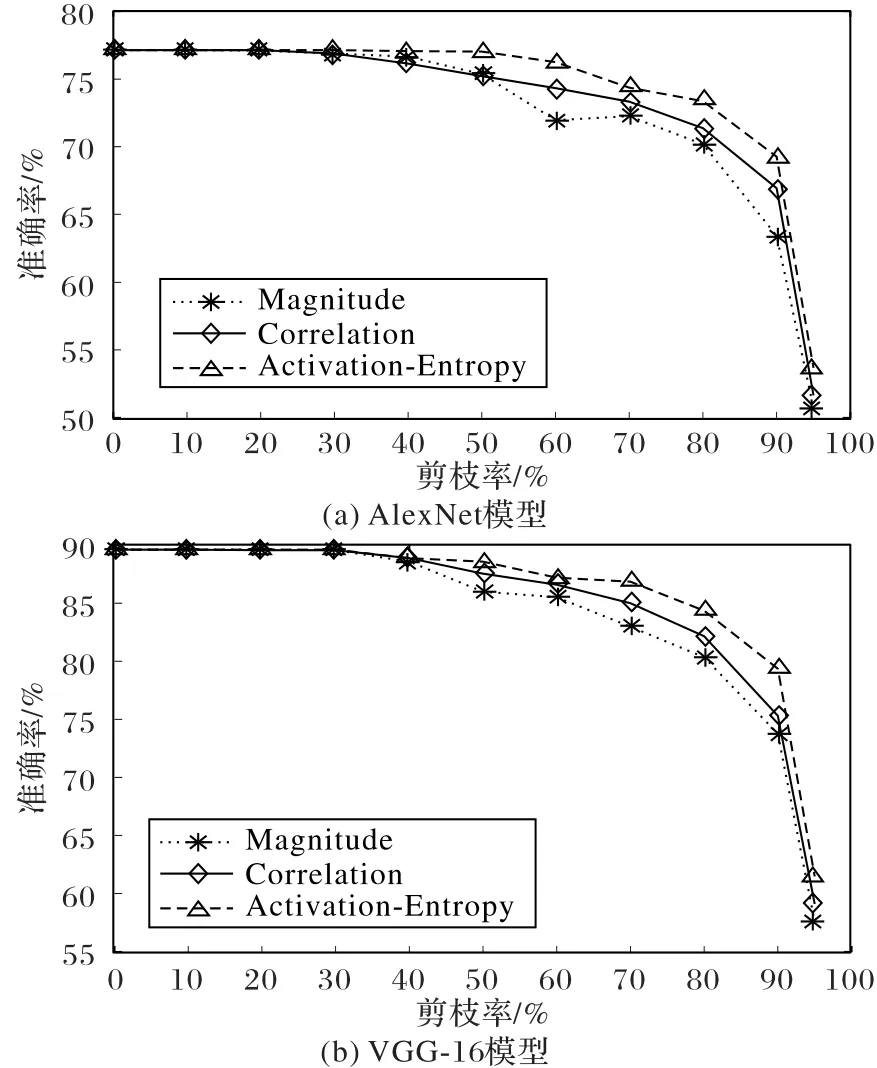
图6 AlexNet和VGG-16模型的fc层的单层剪枝实验结果Fig.6 Single-layer pruning experimental results of fc layer for AlexNet and VGG-16 models
微调可以有效恢复剪枝后的模型精度。微调时设学习率为1×10-4,在整个训练集上重新训练,在微调过程中被裁剪的权重值不会被更新。从图7可以看出,当剪枝率达到95%时,AlexNet模型经过微调后准确率从53.67%恢复到63.15%,VGG-16模型的准确率从61.49%恢复到75.46%。在模型剪枝中,微调是关键步骤,可以有效补偿剪枝带来的精度损失。
3.2.2 分层迭代剪枝实验
本节实验使用基于激活-熵的分层迭代剪枝策略对整个模型进行压缩,比较三种剪枝策略在不同压缩率下的模型精度变化情况,表2显示了AlexNet和VGG-16模型的剪枝实验结果。如表2所示,裁剪权重数量上升,模型压缩率提高,模型准确率下降。经重训练,基于激活-熵的分层迭代剪枝策略:使AlexNet模型压缩了87.5%;准确率下降2.12个百分点,比基于幅度的权重剪枝策略提高1.54个百分点,比基于相关性的权重剪枝策略提高0.91个百分点。使VGG-16模型压缩了84.1%;准确率下降2.62个百分点,比基于幅度的权重剪枝策略提高0.62个百分点,比基于相关性的权重剪枝策略提高0.27个百分点。
实验结果表明,在单层剪枝实验中,相同剪枝率下基于激活-熵的剪枝策略,比基于幅度的剪枝和基于相关性的权重剪枝策略精度损失更小。基于激活-熵的分层迭代剪枝策略能够在模型精度损失较小的情况下有效缩减CNN模型的体积,可以解决CNN模型在移动设备上部署受限的问题。
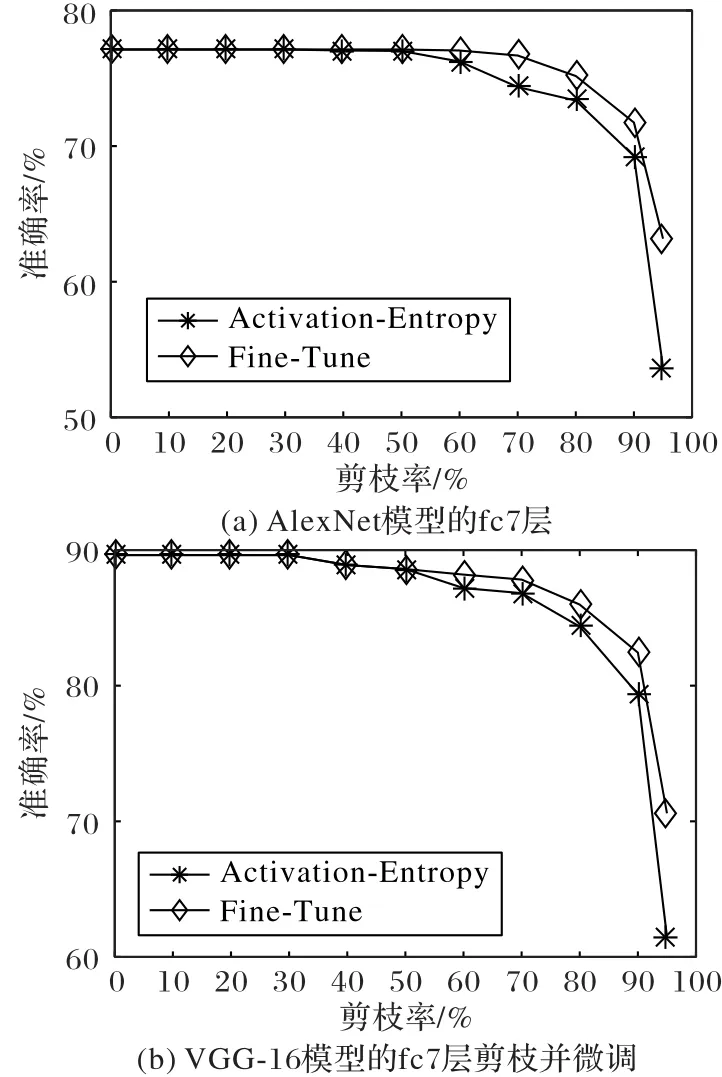
图7 AlexNet和VGG16模型剪枝微调实验结果Fig.7 Pruning fine-tuning experimental results of AlexNet and VGG16 models

表2 AlexNet和VGG-16模型的分层迭代剪枝实验结果Tab.2 Experimental results of layer-wise iterative pruning of AlexNet and VGG-16 models
4 结语
本文分析了现有研究工作中的权值重要性评判方法,提出基于激活-熵的分层迭代剪枝策略裁剪模型中的权重,并使用CSR稀疏矩阵存储裁剪后的权重。实验结果表明,本文提出的剪枝策略能够在模型精度损失较小的情况下有效缩减模型的参数量,解决了模型在移动端的存储问题,使CNN模型在移动设备中的部署成为可能。
