基于前景理论的高铁差异化定价优化方法

秦进，黎熙琼，杨康，徐光明，屈文萱

(中南大学 交通运输工程学院，湖南 长沙 410075)

由于高速铁路的便利性和准时性等突出优点，已经成为我国中长途客运的主要运输方式。既有研究发现，高铁客流在一天中也具有明显的高峰期与平谷期[1-2]。但由于高铁运输都是按照固定的列车开行方案组织列车运行，导致一天中不同时段高铁列车的上座率极不均衡，往往高峰期是“一票难求”，非高峰期列车运能虚靡。客票价格是影响旅客出行选择的重要因素之一。发达国家在航空、铁路和汽运等旅客运输方式中，根据客流特征进行票价的市场化调整，实现了在增加企业效益的同时提高服务水平的目标。但我国高铁客票定价方式的市场化程度仍较低，长期保持服务同OD 对的所有列车票价统一的单一定价模式，未能发挥出价格在调节市场需求方面的基本功能。国铁集团从2016年就开始探索客运票价体制改革，以期在不再增加运力的前提下，提高高铁客运的整体收益。先后在东南沿海高铁、京沪高铁以及京广动卧等线路和产品上的市场化定价实践，均已取得初步成效，也为后续的价格体制改革奠定了一定的理论和实践基础。差异化定价是指将具有相同功能的产品，针对不同的细分市场制定不同价格的一种定价策略[1]。差异化定价是在零售、酒店和银行等领域得到广泛应用并取得成功后，被逐步引入到交通运输领域。郑金子[1]在分析旅客出行选择行为的基础上，提出弹性需求下多列车差异化定价的双层规划方法；李丽辉[2]提出了考虑与其他交通方式竞争的差别定价方法；HETRAKUL 等[3]基于历史客票数据，利用潜在类模型对旅客市场进行细分后，提出了铁路客票定价和座席分配的联合优化方法；李博等[4-5]在对旅客分类的基础上，提出高铁差异化定价方法；李博[6]设计了基于旅客时间价值的高铁非平行车次差别定价优化模型；李雪梅等[7]将旅客分为价格敏感性和时间敏感性2类，提出了考虑竞争的高铁差别定价方法；HU 等[8]研究了动态票价和席位分配的联合优化方法；蔡鉴明等[9]利用潜在类模型对旅客进行细分的基础上，提出了高铁动态差别定价方法；赵鹏等[10]提出了高铁差别定价的双层规划方法；周文梁等[11]提出了弹性需求下的高铁多类列车差异化定价与票额协同优化方法。尽管差异化定价方法已在铁路客运领域得到了一定的研究，但这些研究多是基于期望效用函数或Logit 选择模型，对旅客出行选择进行简单的描述，在这个过程中对旅客的个体差异性往往考虑不足，尤其是缺乏对旅客在出行选择行为中的有限理性特征的描述。本文在利用前景理论分析旅客出行选择行为特征的基础上，以客票收益最大化为目标，构建高铁差异化定价模型，并基于模拟退火算法设计求解方法进行算例的计算与分析。

1 问题分析及变量定义

高铁差异化定价，就是将提供相同运输服务的高铁列车视为同类产品，面向具有不同出行特征的旅客群体制定差异化的客票价格，以实现客票收入最大化的目标。因此，首先要确定高铁旅客分类和合理描述旅客出行选择行为。

旅客分类是指将呈现出相似出行选择行为特征的旅客划分为同一群体进行定价分析[12]。本文将根据既有研究成果进行旅客分类[4]，并基于历史客票数据，统计在不同区间各类型旅客的占比。另外，既有研究往往将旅客视为完全理性人，假设其完全根据效用函数进行出行方式选择。但实际上旅客由于信息不充分等原因，在出行选择中总存在一定的非理性因素。前景理论可以描述人们在不确定条件下的决策特征和规律[13]。JOU 等[14-15]证实可使用前景理论进行交通系统中旅客出行行为决策的分析。因此，为更精准刻画旅客在出行过程中的非理性特征，本文使用前景理论进行旅客出行选择行为描述。

根据前景理论，旅客在进行出行选择时，会预先设定一个心理预期值，即参照点，来权衡判断各个选择方案的优劣[16]。参照点的确定，是假设旅客在了解不同列车票价、发车时刻和旅行时间后，结合历史出行体验，产生的预期心理价格。显然，旅客对票价及时间的敏感程度会影响其参照点的取值。

定义变量如下：给定某高铁线路，共有k个车站，其上运营的列车集合为H，列车h∈H的运输能 力 为C(h)， OD 对(r,s) 的 集 合W={(r,s)|r=1,2,…,k-1,s=r+1,2,…,k}，服务于OD 对(r,s)的列车集为Hrs。对任意OD 对(r,s)和列车h：为列车h的执行票价；为列车h的旅行时间；为第h列车的分配票额数；列车发车时刻为和Urs分别为列车h和总的选择效用；qrs(Urs)和分别为系统和列车h关于效用的需求函数。

记旅客共I类，对第i(i=1,2,…,I)类旅客：为感知的历史广义出行费用；为单位时间价值；为偏好出行时间集合；为(r,s)上的时间敏感度系数；为旅客对期望出行成本的非客观感性认知偏差；为选择列车h而带来的发车时刻偏离惩罚费用；为广义出行费用，为旅客期望出行成本；为选择列车h出行时实际出行成本与期望出行成本的偏离程度；为出行成本偏离对出行决策的影响程度。

为便于分析问题，做如下合理假设：

1)列车开行方案已给定且不会变化。

2)不考虑超售、改签和退票的情况。

3) 不考虑全部列车席位等级区别(只考虑二等座)。

2 模型构建

对于任意OD对(r,s)，偏离惩罚费用是该列车发车时刻与旅客偏好出行时间的偏离程度的函数：

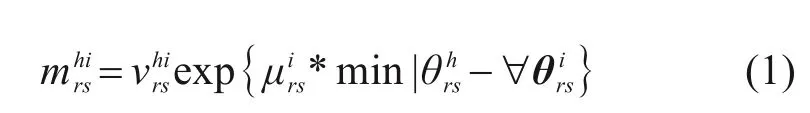
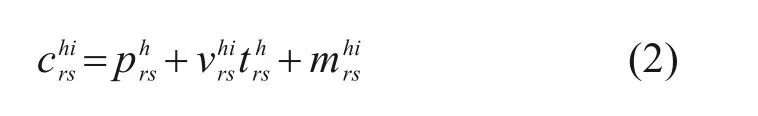
记第i类旅客的预计售票数为则服务于(r,s)间所有列车的平均票价、第i类旅客平均出行时间和对第i类旅客平均偏离惩罚费用，分别计算为：

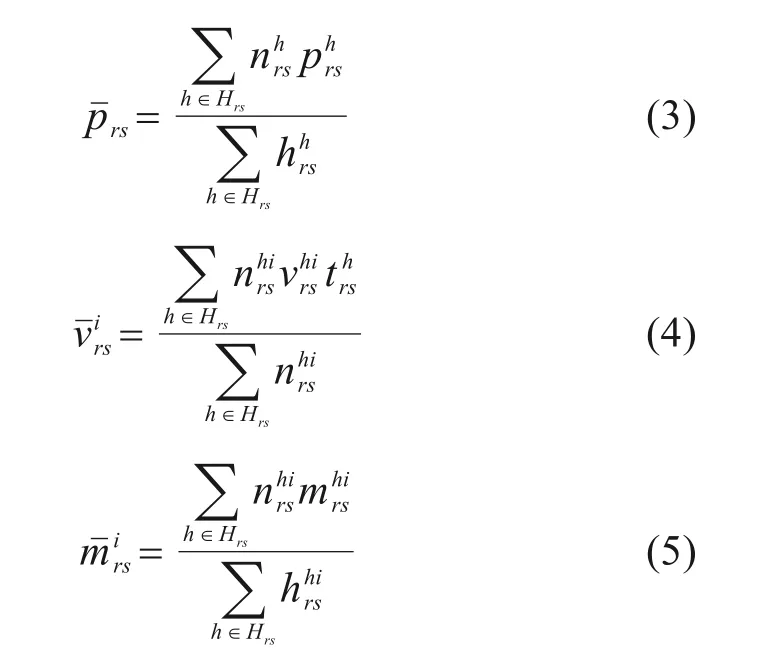
因此，对第i类旅客而言，服务于(r,s)间所有列车的平均出行广义费用为：

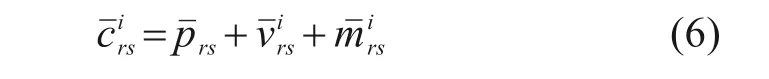
在广义费用的基础上，得到旅客期望出行成本为：

其中：ρ为权重系数。

以旅客期望出行成本作为参照点，OD 对(r,s)间的第i类旅客选择列车h出行后，实际出行成本与期望出行成本的偏离程度为：

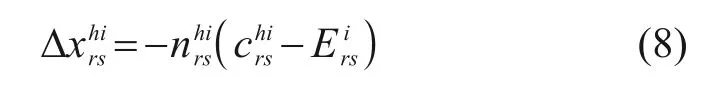
由于出行决策者对于收益的敏感往往低于对损失的敏感，构造决定出行成本偏离对出行决策影响程度的价值函数如下：

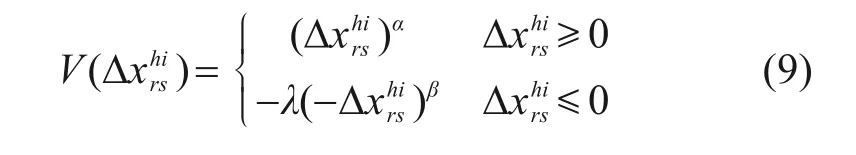
其中：α,β(0 ＜α≤1,0 ＜β≤1)越大，表示旅客对风险越敏感，λ(λ＞1)表示损失规避系数。

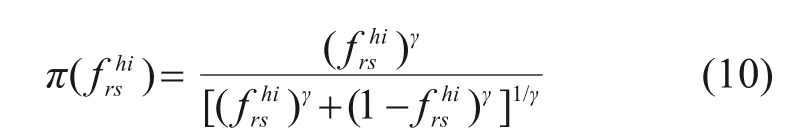
得到期望参照点条件下,旅客选择列车h的效用及系统效用分别为：

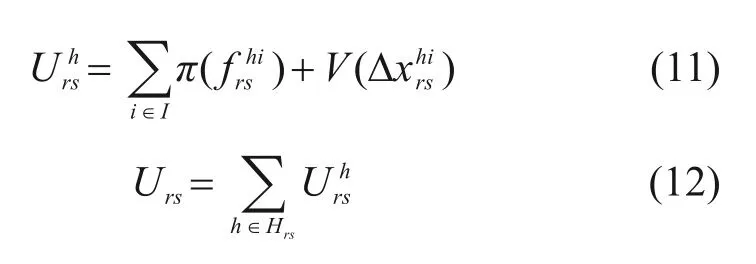
当所有列车的效用之和为正时，高铁吸引潜在旅客出行，使弹性客流增加；效用之和为负时，高铁会流失部分客流。

由于相同OD 间的列车有很强的可替代性，因此高铁出行的弹性需求，应采用服务于相同点对的所有高铁旅客列车的弹性需求进行描述更为合理，记则(r,s)间的弹性需求可描述为：

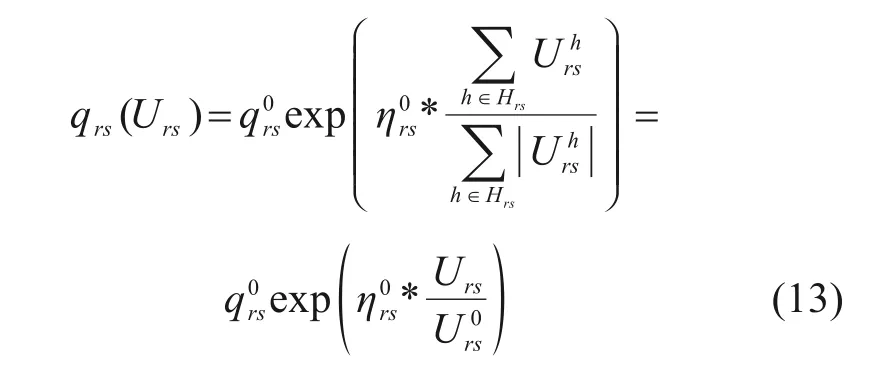
对于服务于(r,s)的列车h∈Hrs，旅客选择该列车的出行需求函数，可通过分解总的弹性需求qrs(Urs)获得。借鉴既有研究成果，假设旅客的选择遵循Multi-Nomial Logit (MNL)模型，则列车h∈Hrs上的弹性需求可表示为：

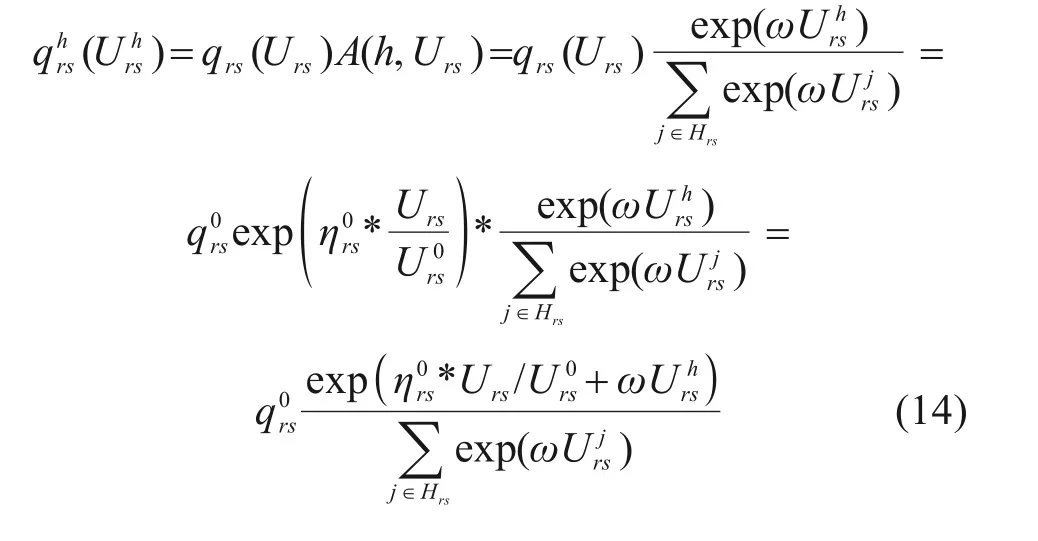
其中：ω为给定的系数参数。

由此，构建基于前景理论的高铁差异化定价模型如下：

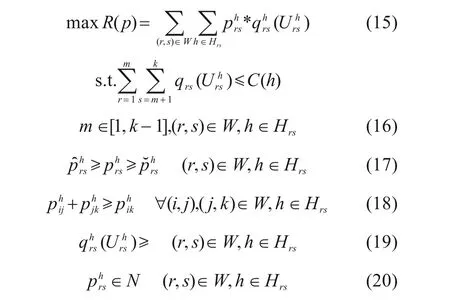
其中，式(15)是最大化客票总收入；式(16)是列车运能(座席数)约束，即对任一区间上的列车h，占用该区间的所有OD 需求之和不应超过列车定员；式(17)和式(18)分别是票价的上下限和不倒挂约束；式(19)和式(20)分别是需求非负和票价整数约束。

3 求解算法

由于高铁线路车站多、运营列车数量多且高铁列车能力大，前面所提出的优化模型计算复杂度很高，很难使用精确算法进行求解。模拟退火算法(Simulated Annealing, SA)是一种基于Mente-Carlo 迭代求解策略的寻优算法，它能概率性跳出局部最优得到趋于全局最优的解[17]。SA 算法还具有使用灵活、较少受初始解限制等优点，因此选用SA进行求解。

SA 算法需基于初始解展开迭代优化搜索。原问题的初始解，可在票价上下限范围内，随机生成相邻车站所构成区间的票价，进一步组合形成任意OD对的票价，由此得到初始票价集p。在此基础上，根据式(1)～(13)得到各OD 的弹性客流，利用式(14)进行配流后，判断各列车是否满足能力约束，若不满足，将该列车多余客流按比例加载到其他列车，直至全部满足能力约束。

对于算法的邻域构造，在当前解p中，随机选择某OD 对(r,s)，对于其票价令Δp=min从(-Δp,Δp)随机产生数值η≠0，由此，令构成原问题票价解的邻域解。

SA 算法的实现，还需对退火计划表进行设置，包括初始温度、温度下降规则、同温度下迭代次数和算法终止规则[18]。初始温度可直接设置为初始解的目标函数值，温度下降规则是按比例(降温系数)下降，同一温度下的迭代次数使用最大迭代次数进行控制，算法终止规则是当前温度低于给定的终止温度时算法终止。

由此，SA算法的详细步骤如下。

Step 1：初始化。生成问题初始解，即初始票价集合p。设置初始温度T0，给定温度下降比例α，终止温度tf，同温度下最大迭代次数L。令当前温度t=T0，当前迭代次数K=1，记当前全局最优解

Step 2：邻域解构造。基于原解p生成邻域解p'。检查p'的可行性，若不可行，则重复上述邻域解生成操作，直至得到满足约束的邻域解。

Step 3：比 较 判 断。若R(p′)≥R()，令p==p′，转Step 5，否则转Step 4。

Step 4：Metropolis 准则检验。记ΔR=R(p)-R(p′)，则较劣解的接受概率为P(A)=exp(-ΔR/t)；从区间(0,1)中产生一个随机数μ，若μ≥P(A)，则令p=p'，否则不接受该较劣解为当前解。

Step 5：K=K+1，若K≥L，则转Step 6，否则返回Step 2。

Step 6：t=t·α，若t≤tf，算法终止，输出最优解否则，K=1，返回Step 2。

4 实例分析

以京沪高铁为例，选择G2，G4，G6，G8，G12，G14，G16 和G18 共8 趟列车为研究对象，各车次的停站方案如图1 所示，共产生15 个OD对。各站发车时刻如表1所示。

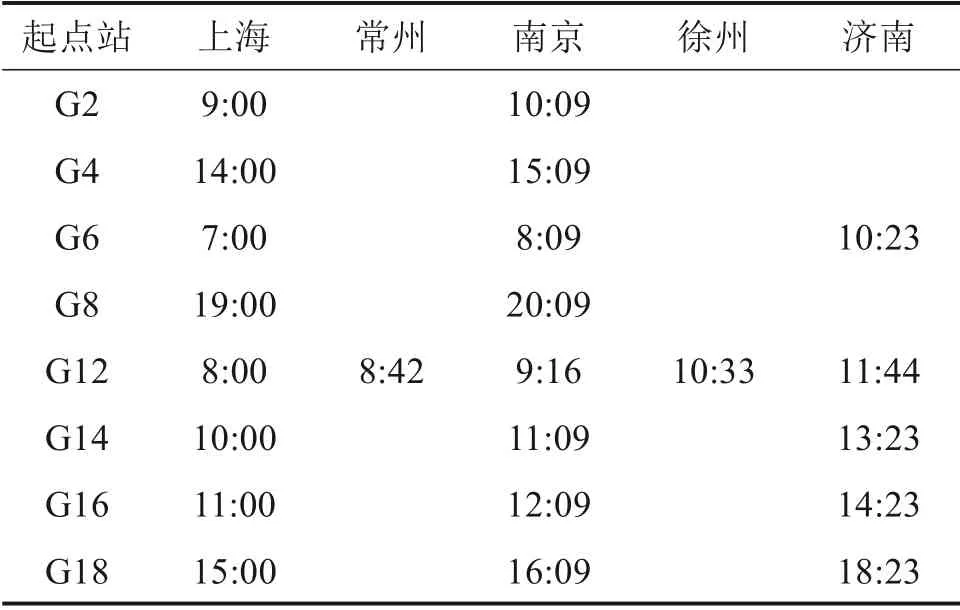
表1 各列车发车时刻表Table 1 Train timetable

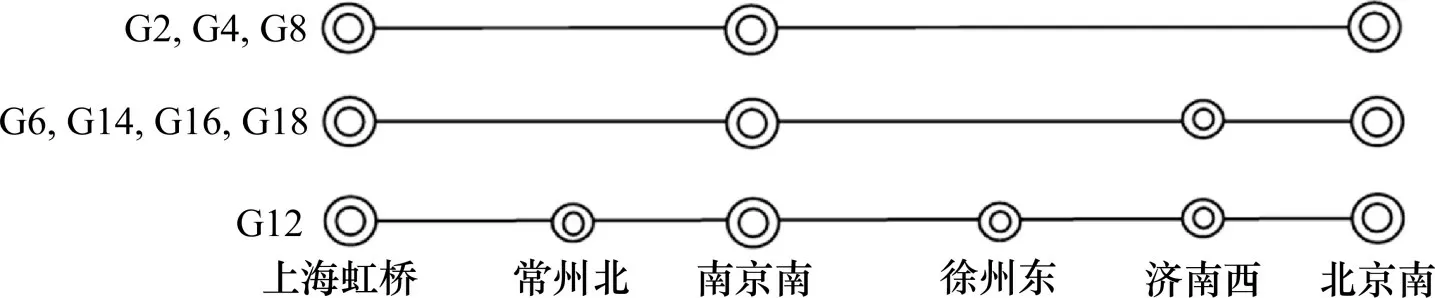
图1 列车停站方案Fig.1 Train stop scheme

所有列车的定员(运能)均为1 005 人。以节假日(2018年5月20日，高峰期)和非节假日(2018年5月23日，非高峰期)2个时段的客流分别进行分析。

根据既有成果[16]，将高铁旅客分为3 种类型，如表2 所示。其他参数取值为：α=β=0.88，λ=2.25，γ=0.61；对任意OD 对(r,s)所有旅客类的时间敏感度系数统一设为和=1.2；由于经济型旅客会占总旅客80%以上，可设置=1.333；旅客初始心理价格为完全理性期望价格，即=0。

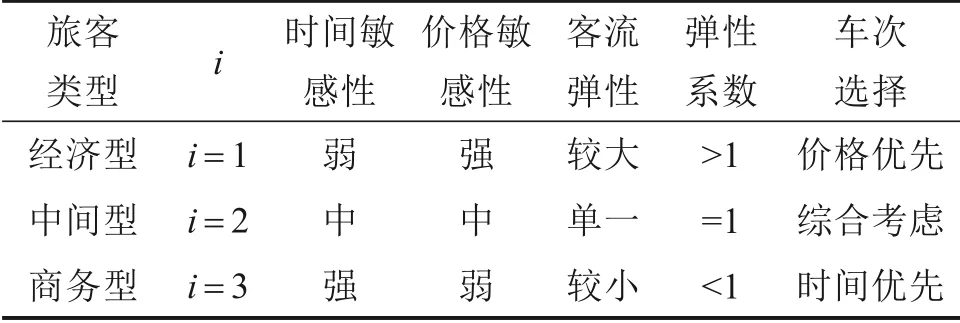
表2 高铁旅客分类Table 2 Classification of the high-speed rail passenger

旅客历史出行经验对出行选择的影响由参数ρ体现，如图2 所示。随着ρ的增加，由于高峰期票价提高，旅客受历史出行经验的影响，高票价往往会抑制他们购票的欲望，使客票收入下降。但在非高峰期，客票收入的增加，是由于票价下降刺激了旅客的出行欲望。但总体而言，总客票收入几乎始终持平。

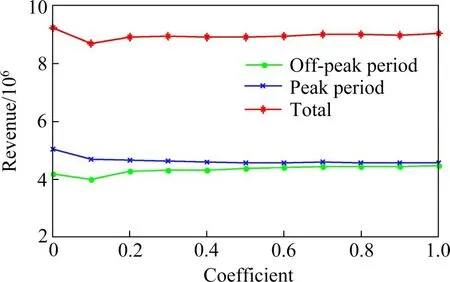
图2 旅客历史出行权重系数对客票收益的影响Fig.2 Ⅰnfluence of historical travel weight on revenue

最优的差异化票价方案如表3所示。高峰期除G18 外的其他列车票价均有所增长，但差异明显，其中G12 的上海—北京区段票价相比初始票价增幅最高，达18.9%(658 元)。同样的，在非高峰期，除G6 外的其他列车票价都有所降低，从而吸引了更多旅客出行。其中，G14的上海—北京区段票价降幅最大，达16.4%(463元)。

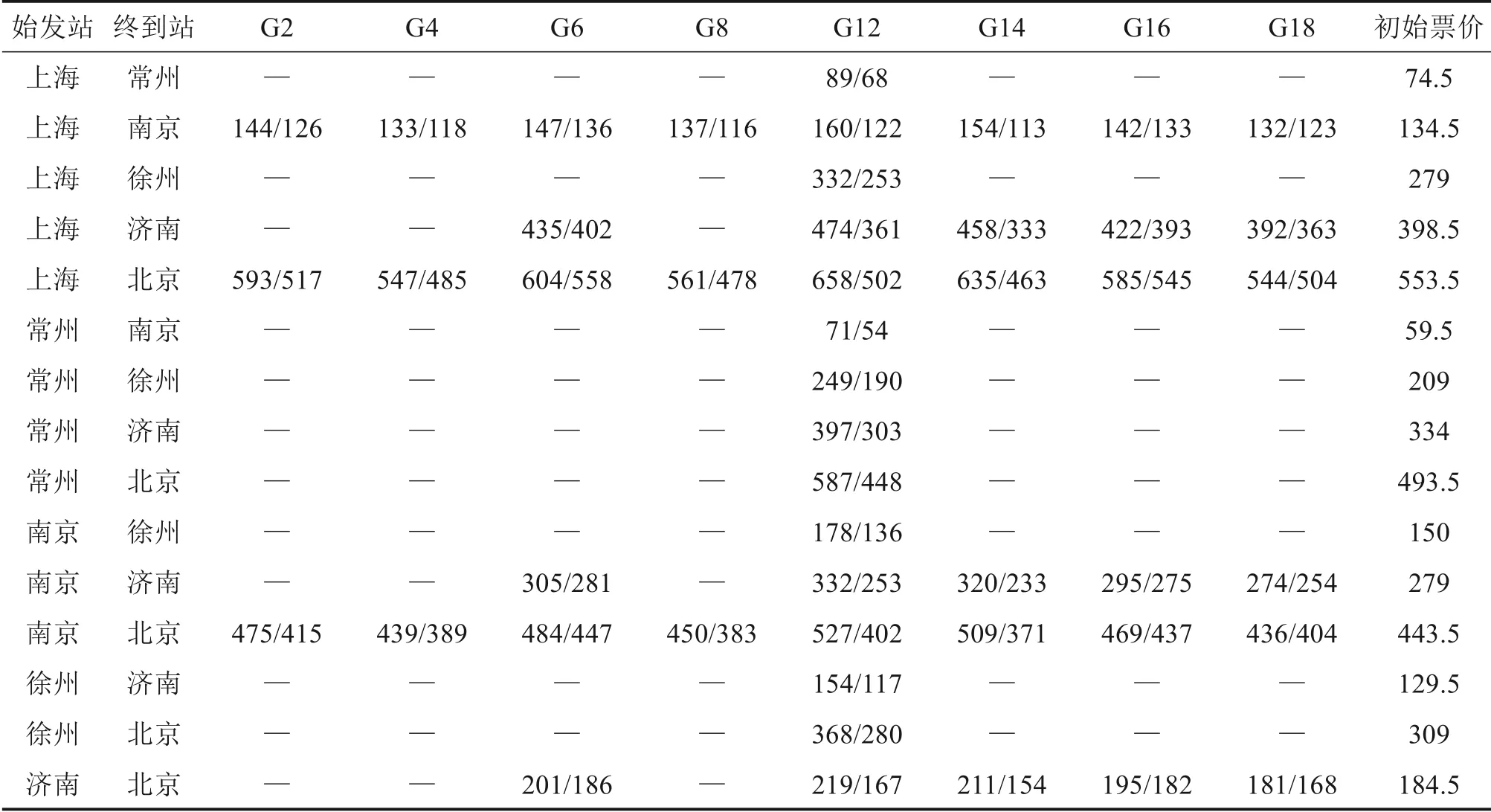
表3 高峰期/非高峰期列车票价情况Table 3 Ticket prices of trains in peak/off-peak hours

高峰期和非高峰期的客流情况如表4所示。其中，由于仅G12在常州和徐州停车，因此这2个车站的需求可视为刚需，客流一直保持稳定。其他OD，在非高峰期时初始客流较小，各列车降价会使客流增长，客流的增长不仅弥补了降低票价的损失，还使总客票收入增长10.41%；高峰期票价提高后，列车仍几乎全部满员，总客票收入相对增加了7.98%。

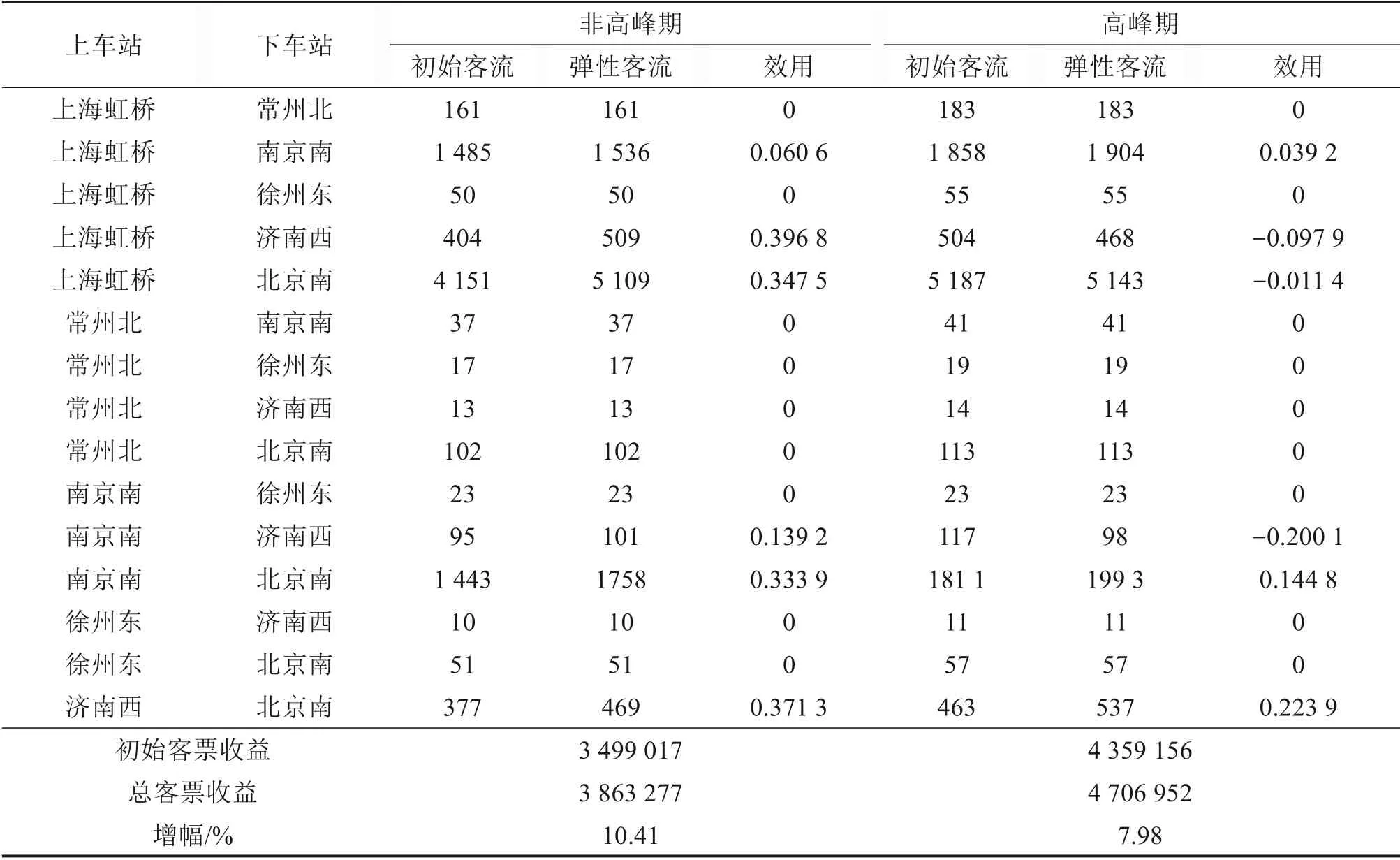
表4 非高峰期和高峰期的客流变化情况Table 4 Changes in passenger flow during off-peak and peak periods

高峰期各OD 间弹性客流和初始客流的变化情况如图3 所示。各OD 间的客流高峰时段并不相同，但对同一OD，弹性客流与初始客流的高峰时刻较为一致。对于距离最长的上海—北京区段，票价提高对客流量的影响最小，相对而言，提高票价后，南京—济南、济南—北京的客流变化较大，这是因为其距离较近，与高铁竞争的交通方式多，价格提高后旅客会有更多的选择。但是总体而言，高峰时段的高铁票价上涨，对旅客的选择影响并不突出。

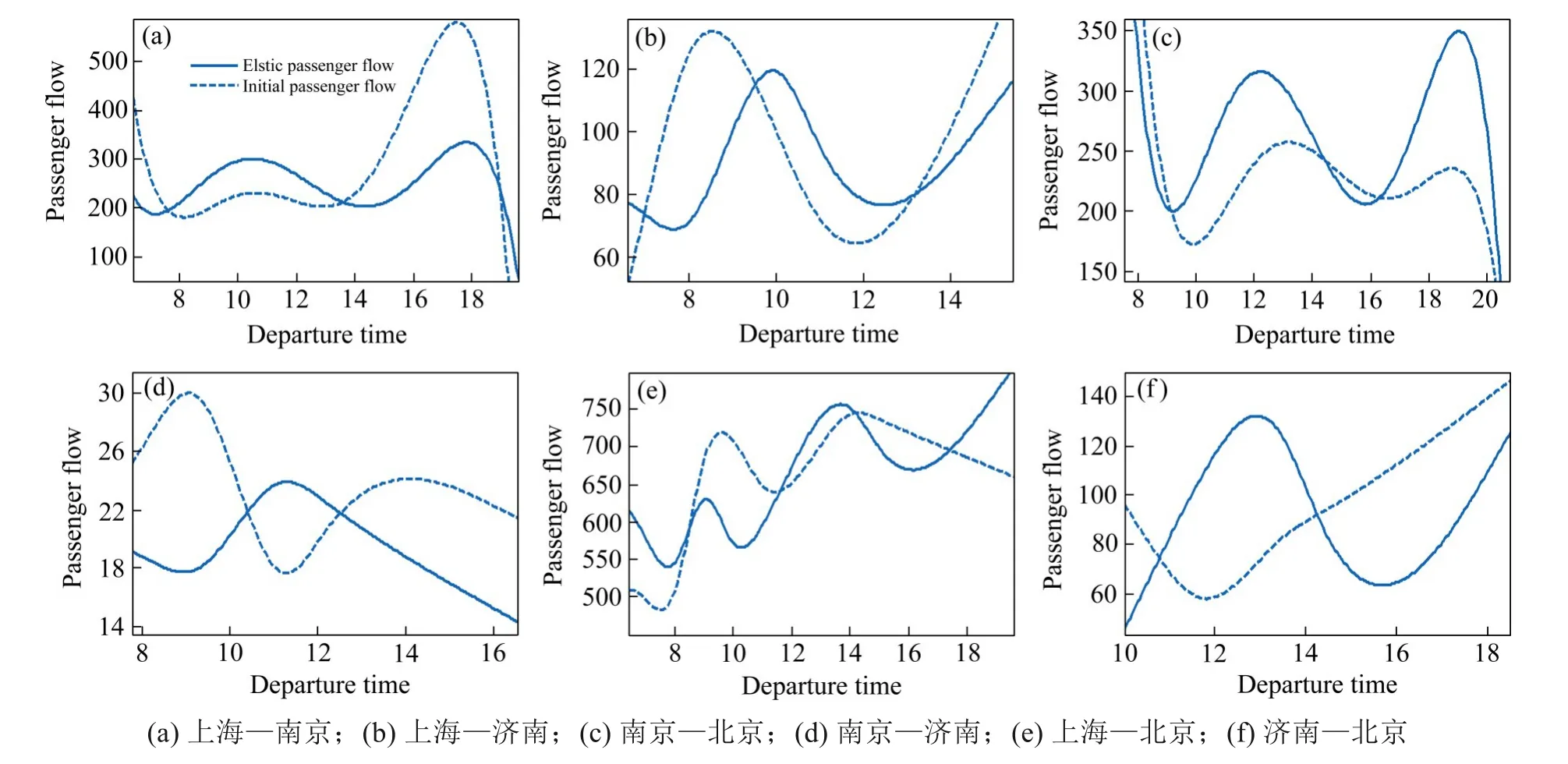
图3 高峰期各OD客流变化情况Fig.3 Changes of OD passenger flow in peak period

与高峰期相比，非高峰期票价的变化会导致客流更显著变化，如图4所示。

以上海—北京和南京—北京2 个距离最长的OD 为例，由于票价降低，吸引大量价格敏感的旅客，客流增长幅度最大。相对而言，上海—南京由于距离短，初始票价不高，因此尽管票价降低，但幅度有限，客流并无明显变化。对于其他OD，总体客流都有小幅度的增长。总的来说，降低票价对增加非高峰客流增加有积极的影响。

旅客期望出行成本受多种因素的影响，除历史出行成本、期望出行时间等确定性因素外，还包括服务体验和运输企业形象等不确定感性认知变量。若旅客对高铁感性认知表现出积极作用，即式(7)中ξ i rs＞0，其值越大，旅客出行选择时的票价期望参照点也就越高，也就愿意支付更高成本选择高铁出行。

从表5 可发现，旅客感性认知值每增长10%，带来的非高峰期和高峰期总客票收入增幅，分别超过9%和3%，这说明提高旅客对高铁出行的感性认知，对高铁收益管理具有重要意义。建议高铁企业可通过塑造企业正面形象、提升服务质量等方式，提高旅客对高铁的正面感知，从而实现高铁可持续发展。

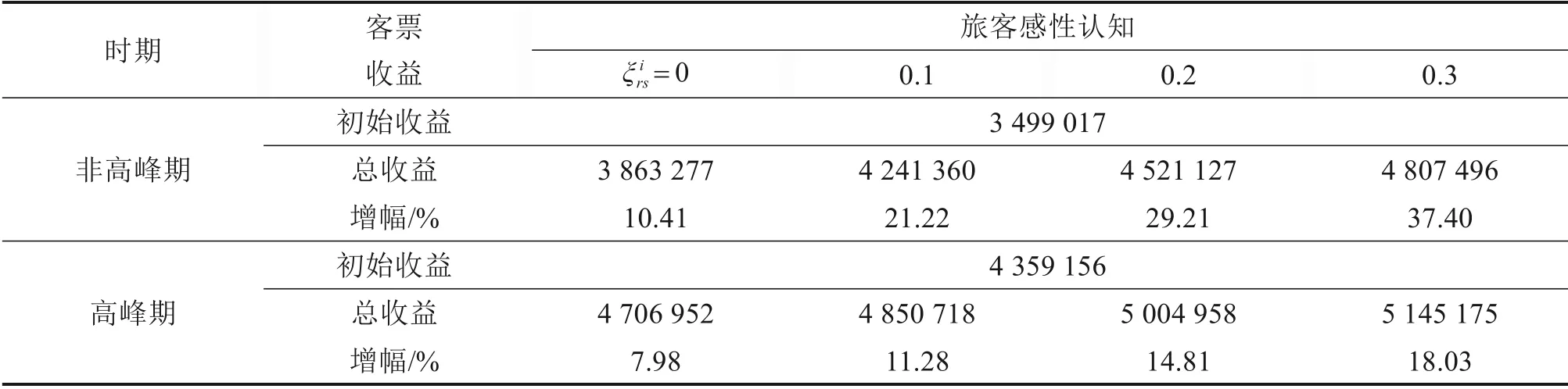
表5 旅客感性认知对客票收益的影响Table 5 Ⅰnfluence of passengers’ perceptual cognition on ticket revenue

5 结论

1) 基于前景理论，将旅客期望出行成本作为决策参照点，以总客票收入最大化为目标，考虑列车运能、票价区间和票价不倒挂等约束，建立高速铁路差异化定价决策模型，并利用模拟退火算法进行求解。

2) 以京沪高铁为例的计算分析表明，合理的高铁差异化定价策略，可以通过在高峰期提价调节客流和非高峰期降价吸引客流，分别实现客票总收入增长7.98%和10.41%，实现了平衡客流和提高收益的双重目标。

3) 旅客对高铁的主观感性认知每增加10%，分别可以将非高峰期和高峰期的总客票收入的增幅再提高9%和3%以上。这表明旅客对高铁出行感性认知的正面作用，可以通过提高旅客的忠诚度和服务期望价格，促进客票收益显著增加。