列车开行方案与客流需求的匹配性评估与优化研究

李科，李刚，吕红霞,3,4

(1. 西南交通大学 交通运输与物流学院，四川 成都 610031；2. 宜宾市南溪区公路养护管理段，四川 宜宾 644100；3. 综合交通运输智能化国家地方联合工程实验室，四川 成都 610031；4. 综合交通大数据应用技术国家工程实验室，四川 成都 610031)

理想条件下的铁路列车开行方案的编制是以客流需求基本保持稳定为前提进行的。然而，在实际的运输生产过程中，由于受到旅客出行习惯、节假日、宏观政策等因素的影响，客流需求会呈现动态变化，容易导致现行开行方案能力虚靡或客流需求无法满足，进而影响线路乃至路网的运输服务质量。所以在列车开行方案初步编制之后、实施之前，对其与客流需求之间的匹配性及时进行评估与优化就显得尤为重要。列车开行方案与客流需求的匹配性[1]是指以合理高效地安排和利用运输资源为原则，充分协调运输能力、服务水平等要素与客流需求之间的关系，从而实现运营方与乘客方双赢的目的。现有的列车开行方案评价研究主要从盈利水平[2]、服务水平[3]以及综合水平[4-6]的角度构建评价体系，王文宪等[7]提出了开行方案与客流需求适应性的概念，但所选用的集对分析法无法消除指标间的多重共线性。现有的开行方案优化主要以保障经济效益或社会效益建立单目标优化模型[8-9]，及以保障两者综合效益最优建立多目标优化模型进行求解[10-12]，但大多优化问题都独立于开行方案的评价，优化与评价模型之间缺乏有机统一。因此，本文从能力效用、运输质量以及服务水平3方面多维度地构建列车开行方案与客流需求的匹配性评估体系，并通过解析各指标之间、指标与开行方案之间的关联性，以TOPSⅠS 法为评估主体，同时引入因子分析消除指标间的高度相关性，熵值法修正指标权重，最后针对评估结果较差的开行方案，建立基于匹配度评估模型嵌套的列车开行方案双层优化模型，并结合案例检验评估体系与优化模型的效果。

1 基于因子分析的E-TOPSⅠS 匹配性评估体系

1.1 匹配性指标的选取

为合理构建匹配性评价指标体系，本文基于指标的方便获取与计算、主客观结合、多维度和全面等原则，从能力效用、运输质量以及服务水平3 方面进行综合分析与比较，提炼出以下6 个匹配性指标。

1) 线路平均满载率A1：线路满载率是从线路层面反映铁路能力效用的指标，即运营时段内线路单向各断面客流量与该断面实际运力的平均比值：

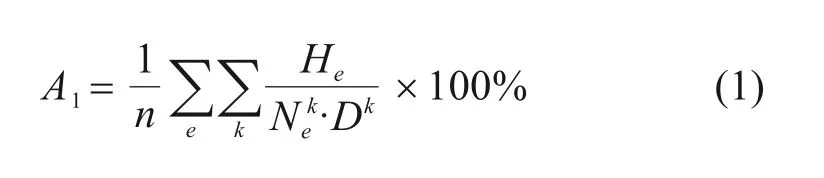
式中：n为断面数；He为第e断面单向客流量；N k e为经过第e断面列车k的数量；Dk为列车k的定员。

2) 列车平均客座率A2：列车客座率是从列车层面反映铁路能力效用的指标，即实际发生的客流总周转量和列车所提供的客座总公里之比：

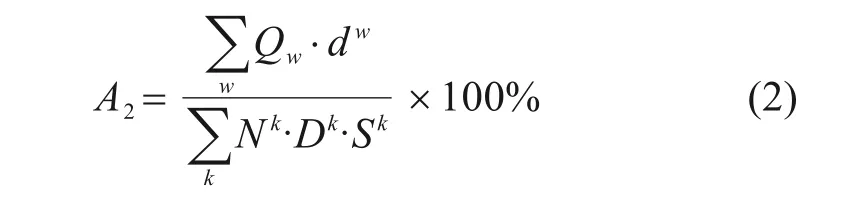
式中：Qw为各OD 对间w的客流量；dw为各OD 对w间的运行距离；Sk为列车k的单次运行里程。

3) 车站平均停站率B1：车站停站率是从车站层面反映车站运输质量的指标，即线路各中间站办理列车停站作业的次数与总服务次数之比：

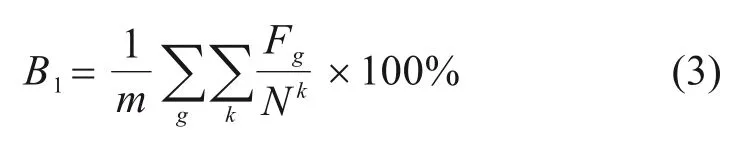
式中：Fg为车站g所办理的停站作业次数；m为线路中间站的数量。

4) 停站损失时间B2：停站损失时间是从旅客层面反映列车停站质量的指标，即因列车为满足中间站上下乘客的需要而导致车上其他旅客被迫产生的额外时间损失：

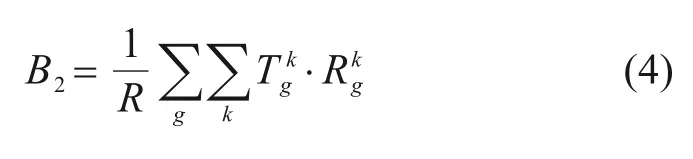
5) 候车损失时间C1：候车损失时间是以各站发车频率反映服务水平的指标，即旅客自进站后开始、到上车前所结束的这一候车行为过程所花费的时间：

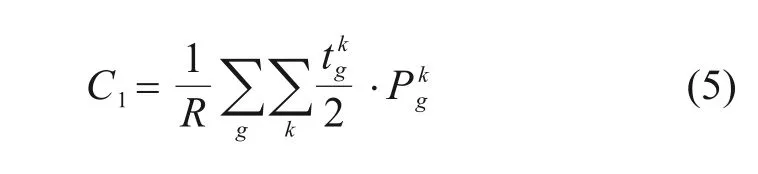
6) 单位时间拥挤度C2：旅客拥挤度是以单位时间内客流拥挤程度反映服务水平的指标，即旅客在乘车过程中对列车所载人数的主观体验：

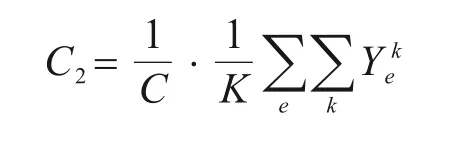
其中

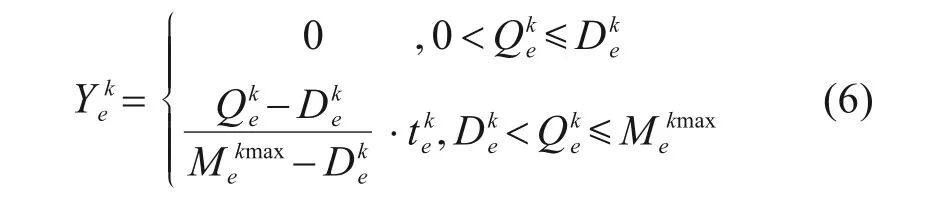
式中：C为列车平均运行时长；K为列车种类数；为k类车在断面e的运行时间；与分别为列车k在断面e所能提供的总坐席运力与总额定运力。

进一步分析可知，A1，A2和B1为效益型指标，分别从线路、列车和车站角度反映了运营方的利益；B2，C1和C2为成本型指标，分别从候车、停站和舒适性的角度反映了乘客方的利益。同时，A1，A2和C2对列车开行对数影响显著，B1，B2和C1对停站方案产生影响。各个指标相互作用，相互制约，又与开行方案相互关联，开行方案优化目的，正是通过调整开行对数、停站方案等内容，实现两者匹配度的综合最优。

1.2 匹配性评估方法

考虑到匹配度指标之间相关性强，冗余度高，本文采用基于因子分析的E-TOPSⅠS 法[13]进行综合评价。因子分析可削弱评估指标间的相关性，熵值法可利用数值变化程度修正因子权重，TOPSⅠS法又可弥补间接距离得到因子总得分的不足，3 种方法互为呼应，相辅相成，评价结果更加合理、严谨。

1.2.1 基于因子分析及熵值法的指标权重

1) 规范化决策矩阵。根据m天不同日期的客流需求与n个匹配度评估指标，构建决策矩阵U=(uij)m×n，并通过正向标准化操作得到规范化矩阵R=(rij)m×n。

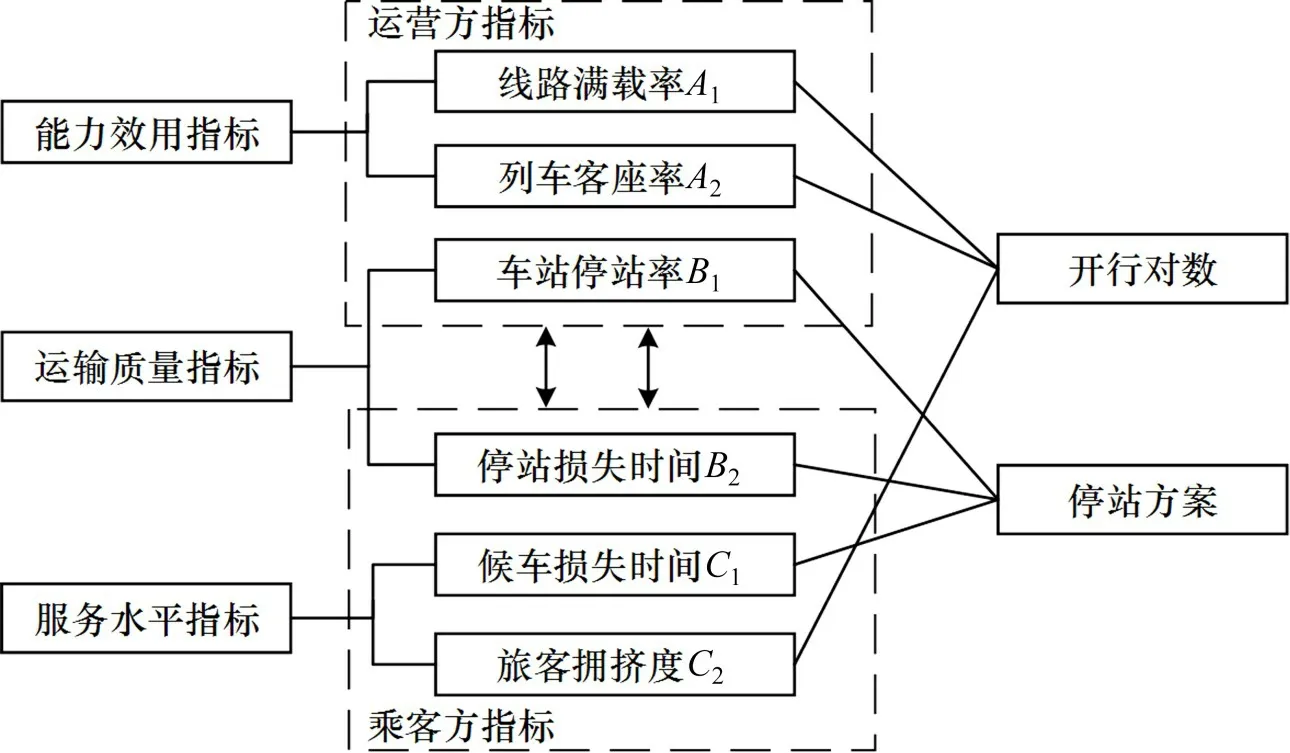
图1 指标关联图Fig.1 Ⅰndex correlation graph

2)因子分析法确定权重。

①将规范化矩阵转化为相关系数矩阵，进行指标间的相关性检验；

②按照解释总变差大于85%的原则提取τ个公因子(其中τ≤6)及与子对应的贡献率hτ；

③对成份矩阵进行正交旋转，从而得到指标对应各自公因子的得分系数βj。

3)熵值法修正权重。

②计算指标xj的差异性系数：gj=1-ej，gj表示指标在评价结果中的影响力。

③用差异系数gj对因子分析方差贡献率hτ和成份得分系数βj进行修正：从而构建指标xj的权重向量ω=(ω1,ω2,…,ωn)T。

1.2.2 基于TOPSⅠS的综合评估

1) 根据指标的权重向量ω与规范化矩阵R构成加权矩阵P=(pij)m×n，其中pij=rij×ωij。

3) 计算各日期样本与V+和V-的距离：d+i=并得到相对贴近度其中Di∈[0,1]。

4) 对各样本的匹配性进行综合评估。Di的大小是对评估对象与最优解之间距离程度的体现，Di越大，说明样本对象同最优解越靠近，匹配度也就越高；反之匹配度越低。

2 基于评估嵌套的开行方案双层优化模型

通过评估体系所得到的列车开行方案与客流需求的匹配度如果低于预先设定的阈值，便需要针对相应时期的列车开行方案进行基于匹配性的优化。开行方案优化模型按照层次结构可分为单层优化模型[9-12]与双层优化模型[8,14]，本文结合前文评估模型，同时考虑到客流分配的需要，建立基于匹配度评估嵌套的列车开行方案双层优化模型。

2.1 符号假设

模型的变量参数假设如下：设铁路单向线路为L=(S,E)，其中：S=(si|i=1,2,…,n)为车站集合；qij为在车站si上车，车站si下车的人数；E=(ew|w=1,2,…,m)为OD区间集合；dw为区间ew的里程；qw为区间ew的出行人数；R=(ro|o=1,2,…,n-1)为单向断面集合；qo为断面ro的客流量；Dmax为列车最大载客量。设开行方案集合Ω(k,fk)，其中：k=为停站方案集合；为0-1变量，若列车在si站停车，则=1，反之=0；fk为采用k类停站方案的列车对数。为OD 对w间旅客选择的k类车发车周期；为OD对w间旅客选择的k类车平均停站时间；为OD 对w间旅客选择的k类车平均停站次数；为OD 对w间乘坐k类车的累计客流量。θ1，θ2和θ3分别为候车时间损耗、停站时间损耗及拥挤度的权重，γ1，γ2和γ3分别为三者的成本系数。

2.2 上层匹配度模型

上层模型的目的主要是协调运营单位与旅客两者的利益从而达到综合最优。由评价体系可知，6 个指标不仅代表着列车开行方案中开行对数、停站方案的质量，又能从各个方面反映运营方与乘客方的利益，所以本文以匹配度最优为目标构建上层模型：

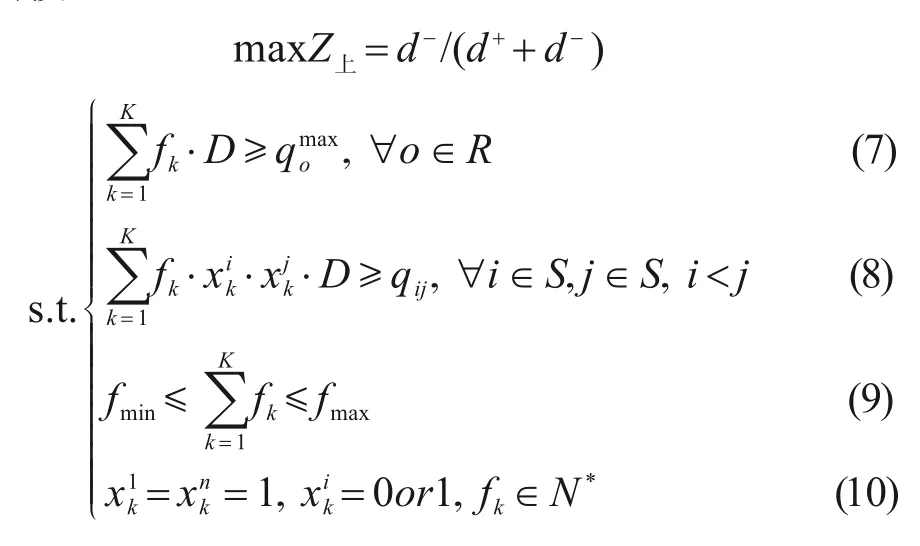
式(7)为客流基本出行需求保障约束；式(8)为客流停站需求保障约束；式(9)为最低开行对数标准及线路最大能力约束；式(10)分别为始发终到停站约束、0-1约束与开行对数的正整数约束。

2.3 下层客流分配模型

客流分配是指将列车运行网络中的各个列车看作承载路径，客流作为待分配单元，将各OD 区间的客流按照旅客的出行行为机制的不同分配到相应列车上。根据效用最大化理论，乘客在出行前总是偏向于广义费用相对较小的方式选择，所以本文以乘客广义费用最小为目标构建下层用户平衡配流模型：

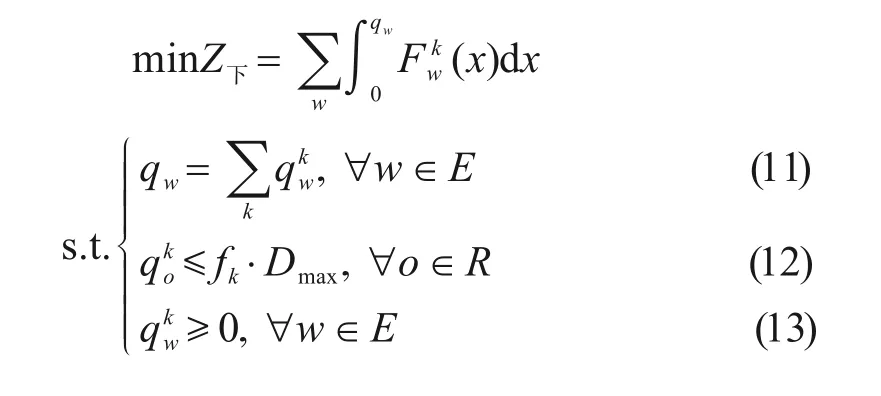
其中，式(11)为客流平衡约束；式(12)为列车最大载客能力约束；式(13)为分配数值的正向约束。F kw为广义出行费用阻抗函数，主要包括候车时间损耗、停站时间损耗及拥挤度3部分，即：

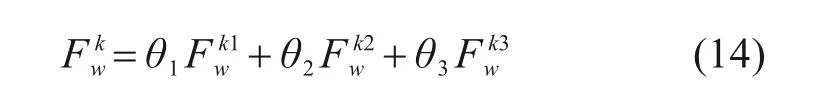
拥挤度函数：

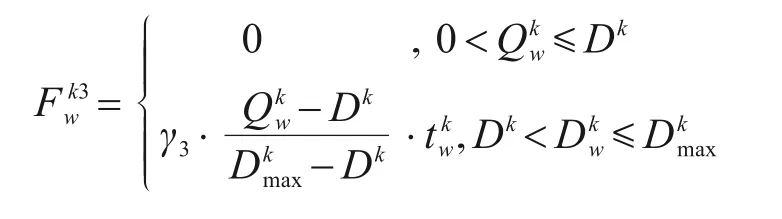
综上所述，本文最终构建以匹配度最优为上层、客流平衡分配为下层的开行方案双层优化模型，并结合模型特点，使用基于嵌套MSA 配流的粒子群算法[15]进行求解。

3 案例分析

以某城际铁路Y 线所编制的往后一个月的开行方案为例，检验评估体系与优化模型的有效性。Y 线全长45 km，设车站8 座，开行CRH6A 型列车，4 节编组，列车定员与最大载客分别为300与360 人/列，最高运行速度120 km/h。设定线路运营时段为7:00～21:00；列车在始终站停站5 min，中间站2 min；最低开行对数及线路最大能力分别为20，50对/h；θ1，θ2和θ3的权重参考权重向量ω，γ1，γ2和γ3分别取0.4，0.5 和0.8 元/min；列车种类k与停站方案对应，客流数据通过现有客流数据预测及客流分配模型得到。

3.1 Y线开行方案与客流需求的匹配性评估

1) 计算规范化矩阵：根据匹配性指标式(1)～(6)计算Y线未来一个月内6个指标的数值，并通过正向标准化处理转化为规范化矩阵R=(rij)30×6。

2) 相关性检验：计算相关系数矩阵，线路满载率与列车客座率、旅客拥挤度的相关系数分别为0.745和0.801，车站停站率与停站损失时间、候车损失时间的相关系数分别为0.776和0.810，说明指标间相关性较强，同时KMO和Bartlett的检验值分别为0.792 与0. 000，各项检验系数表明本文指标数据适用因子分析。

3) 计算成份得分系数：按照成分矩阵中解释总变差大于85%的原则提取主成分2个，可累计解释原始数据90.710%的变差，并计算6个指标在各自共因子上的成份得分系数，如表1所示。

由表1 可知，A1，A2与C2在主成分L1 中拥有较大的载荷(0.894，0.853 和0.807)，将其视为开行对数主成分；B1，B2与C1在主成分L2 中拥有较大的载荷(0.833，0.912 和0.677)，将其视为停站方案主成分。

表1 贡献度与成份得分系数Table 1 Contribution degree and component score coefficient

4)利用熵值法计算矩阵R差异系数gj，得修正后的各指标权重ω=(ω1,ω2,…,ω6)T，如表2所示。

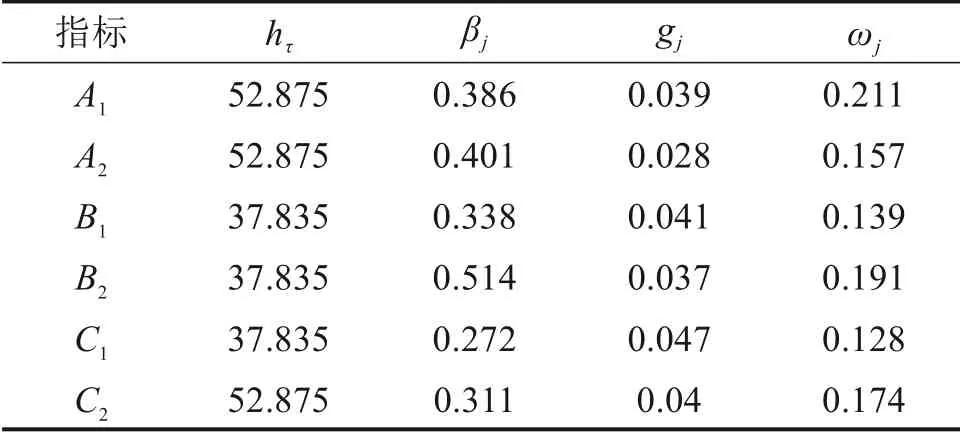
表2 指标权重系数Table 2 Ⅰndex weight coefficient

5)构建加权矩阵P=(pij)30×6，计算6 个指标的最优解、最劣解以及30 d 的样本对象与两者的距离，并得到相对贴近度即匹配度如图2所示。

由图2可见，列车开行方案与客流需求的匹配度在时段6～12 和18～28 较高，说明继续沿用现有的开行方案仍能达到良好的运营效果；但是在月中14～18 时段两者的匹配度较低，说明现有的开行方案(特别是在开行对数方面)已经无法满足该时段客流的需求，对该时段便需要使用开行方案双层模型进行优化。

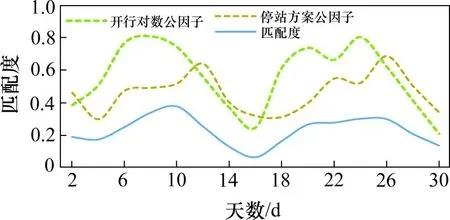
图2 各日公因子与匹配度得分Fig.2 Each day common factor and matching score

3.2 Y线低匹配度时段的优化及分析

根据设定的线路概况、客流数据及相关参数，对14～18 号时段运用Matlab 2018b 编程嵌套算法求解双层模型，连续执行4次操作，粒子群迭代至28 代左右趋于平稳，得到匹配度最优的开行方案如图3所示。

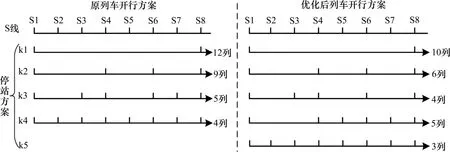
图3 列车开行方案优化前后对比Fig.3 Comparison of train operation scheme before and after optimization

对比原始方案可知，Y线优化后的开行总列数减少2 列，列车客座率提高5.7%，但旅客拥挤度提高了1.4%；列车停站方案由4 类变为5 类，停站次数不变，停站率增加了2.5%。列车开行方案与客流需求的匹配度方面，14～18 号时段的运营方指标与乘客方指标有明显的改善，平均匹配度提升了0.201，说明优化之后的开行方案更加适应客流需求，从而验证了评估与优化模型的合理性与有效性。

4 结论

1)从能力效用、运输质量、服务水平3个方面以及不同维度的6个指标构建评估指标体系，并采用基于因子分析的E-TOPSⅠS 综合评估法，通过因子分析削弱指标间高度相关性，熵值法客观修正指标权重，TOPSⅠS法弥补间接距离计算的不足，3种方法相得益彰，使得评价结果更加客观、科学、严谨。

2) 统一了评估模型与优化模型，根据开行方案与客流需求相互关系，将评估模型作为上层模型嵌套进双层优化模型，结合下层客流分配模型，共同对匹配度较低时段的开行方案进行优化，并通过案例分析验证了本模型能进一步协调运输效率与客流需求，在提高匹配度的同时实现运营方与乘客方的双赢。

3) 本文是基于客流量不变的情况下展开研究的，然而实际中的未来客流具有不确定性，具体表现为客流的波动性以及开行对数、停站方案等开行方案本身变化对客流的影响，后续可基于客流的动态变化对两者的匹配度进行优化研究，为进一步优化列车开行方案提供决策依据和指导建议。