胶合木连续梁抗弯性能试验研究

陈爱军，白帆，周彦，贺国京，王皓磊，王解军

(中南林业科技大学 土木工程学院，湖南 长沙 410004)

胶合木结构作为现代木结构的主要类型之一，结合了国内外现代加工技术，力学性能得到了较大的提升，已逐步应用于我国现代化建筑、桥梁建设事业当中[1]。如湖南省张花高速木结构人行天桥就是以胶合木结构为主要承重结构的现代胶合木结构桥梁[2]。然而胶合木简支梁有着刚度不足、整体变形较大、跨度受限等问题[3]，使其在实际工程中的应用尤其是桥梁工程中的应用受到了较大的限制。采用连续梁的结构形式可以有效降低梁跨中弯矩和变形，进而充分利用胶合木材料性能[4]，是提升胶合木梁跨越能力的有效手段。关于胶合木梁的抗弯性能，国内外学者也进行了大量的试验与理论分析。KLAPÁLEK 等[5]研究了木节的分布对胶合木简支梁强度的影响，并建立了有限元模型，预测了该区域的弯曲受力行为，结果表明木节处存在明显的应力集中现象，对梁的承载能力有较大的影响。TSALKATⅠDⅠS[6]研究了加筋胶合木梁的抗弯性能，并进行了有限元模拟，结果表明加筋后胶合木梁的极限承载力与延性性能均明显强于无筋胶合木梁，破坏模式由脆性转为延性。DE 等[7]研究了胶合木简支梁、加筋胶合木简支梁、预应力胶合木简支梁三者的抗弯性能，并建立了具有非线性应力-应变路径的钢-木组合结构理论模型。FOSSETTⅠ等[8]研究了FRP 加固胶合木梁的抗弯性能，结果表明FRP 加固后试验梁的破坏模式由梁底受拉破坏转为梁顶受压破坏，FRP 加固后试验梁强度大致提高25%，延性提高40%。ZHANG 等[9]对实心、空心和类似竹的矩形胶合木梁进行了弯曲性能试验，同时基于有限元软件对加劲肋的合理间距和厚度进行了参数分析，结果表明在空心胶合木梁内部布设加劲肋后，梁承载力得到了显著提升；并建议加劲肋间距为1.0～3.4 倍梁高，加劲肋厚度为0.25 倍梁宽。周先雁等[10]对胶合木简支梁进行了荷载试验，探讨了梁的破坏形态，分析了抗胶合木梁的抗弯性能。MATTHⅠAS[11]研究了布置形式对胶合木连续梁的影响，对单跨胶合木简支梁、2 跨胶合木连续梁与3跨胶合木连续梁进行了有限元计算，研究表明相比单跨胶合木简支梁，2 跨胶合木连续梁抗弯承载力提升了25%，3 跨胶合木连续梁提升了8%。MAURⅠCE等[12]研究了2 跨胶合木连续梁的抗弯性能，结果表明胶合木连续梁破坏前部分表现为弹性，部分则表现为塑性，破坏模式集中表现为某一加载点与跨中支座间的双铰破坏。王文博等[13-14]研究了预应力对胶合木连续梁受弯性能的影响，结果表明预应力胶合木连续梁较预应力胶合木简支梁的抗弯承载力提高了40%；随预应力调控幅度的提升，梁抗弯刚度也随之增大。国内外学者主要以胶合木简支梁为研究对象，围绕其材料以及抗弯、抗剪、疲劳等方面进行了大量研究，而对于胶合木连续梁的研究较少。本研究在前期研究的基础上[15-21]，以胶合木连续梁为研究对象，并将相同高跨比下不同截面高度的胶合木连续梁和简支梁进行跨中集中荷载试验，探究胶合木连续梁的破坏模式与变形规律，明确胶合木连续梁的抗弯性能，为胶合木连续梁的研究与应用提供参考。

1 试验概况

1.1 试件材料与设计

以国产速生东北落叶松小径材为基材，干燥处理后含水率为9%～11%，经筛选胶合后制造了8组共24根胶合木梁。其中H92-J，H106-J，H119-J，H133-J 为单跨胶合木简支梁；H92-L，H106-L，H119-L，H133-L 为2 跨胶合木连续梁(试验梁参数见表1)。

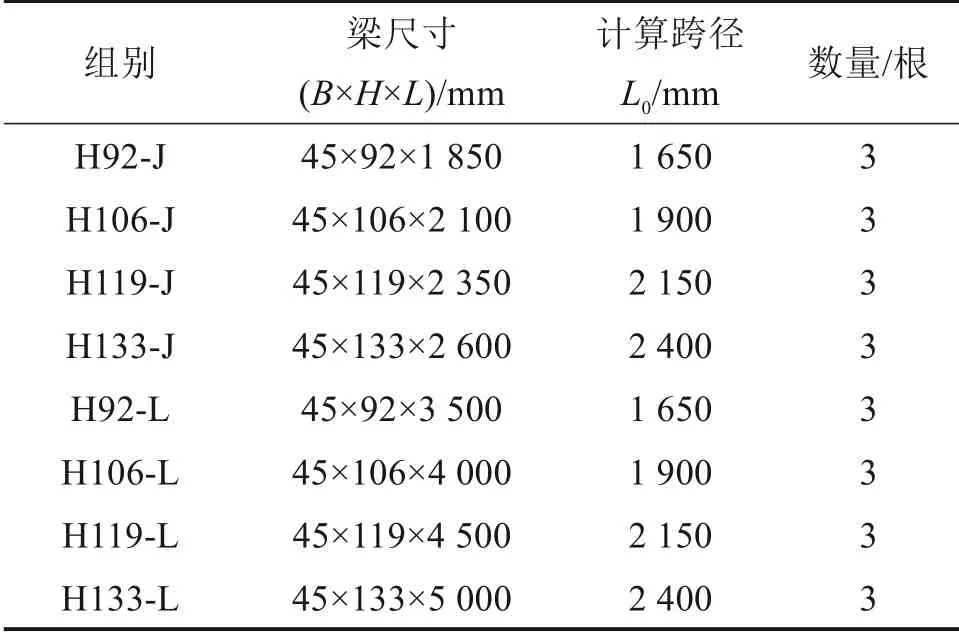
表1 胶合木试验梁分组及参数汇总Table 1 Summary of grouping and parameters of glulam test beams

根据课题组所进行的材性试验，试验采用胶合木的木材平均干密度ρ为0.58 g/cm3，木材顺纹抗拉强度为84.09 MPa，木材顺纹抗压强度为36.49 MPa，木材抗弯模量为9 984 MPa。

1.2 试验装置与试验方法

胶合木连续梁、简支梁加载布置如图1 和图2所示。对梁跨中施加单点集中荷载，加载设备为20 t的液压千斤顶。加载位置与试验梁接触处设置垫块从而防止胶合木梁发生局部破坏。以胶合木连续梁、简支梁的跨中加载处截面为控制截面，在控制截面沿高度方向等间距布置应变片测应变，在控制截面、两端支座处布置百分表测量位移。

图1 胶合木试验梁加载装置示意图Fig.1 Schematic diagram of glulam test beams loading device

图2 加载试验装置Fig.2 Loading test device

在正式加载前对试验梁进行预加载，预加载值取极限荷载计算预估值的5%，用来检查试验仪器是否正常工作以及消除梁与支座、仪器之间的不良接触。正式加载采用线性分级加载的方式，从开始加载至试验梁破坏全程由荷载控制，胶合木连续梁、简支梁加载步均为1 kN一级。

2 试验结果

2.1 试验现象与主要破坏模式

1) 4 组胶合木简支梁在荷载下的试验现象相似，以H92-J 为例：①在加载初期，试验平稳进行，梁处于线弹性阶段。②当荷载由8 kN 渐渐加载至9 kN 时，梁发出细微的木材撕裂声；当荷载加载至10 kN 时，木材的撕裂声愈加明显，荷载加载效率明显降低。③当加载到10.9 kN 时，梁跨中下缘突然发生断裂，梁发生脆性破坏。当荷载加载至梁的临界破坏荷载值时，各组梁的破坏形态有所不同：H106-J 破坏时梁下缘的裂缝向上延伸到胶合木黏合层，并沿顺纹方向延伸，且伴随较大的木纤维撕裂声；H119-J 破坏时裂缝数小于H92-J，但在梁底有2条明显的顺纹裂缝和1条沿梁高方向的横纹裂缝；H133-J 的裂缝首先发生在梁底下缘，达到极限荷载时梁的下缘与上缘均出现了明显的顺纹裂缝和横纹裂缝(见图3(a)～3(d))。

图3 胶合木简支梁破坏形态Fig.3 Failure modes of simply-supported glulam beams

2) 胶合木连续梁试验现象与简支梁不同，以H92-L 为例：①在加载初期，梁跨中的竖向位移随荷载线性递增，中支点处梁向上微微弯曲。②荷载加载至18～19.5 kN 时，可以听到轻微的木材撕裂声；荷载继续增加，梁跨中变形明显，木材撕裂声也逐渐增大。③荷载加载至24 kN 时，试验加载效率显著下降，梁跨中竖向位移增长明显，此时可以清楚听到支座挤压木材的声音，连续梁中支点处已有明显的局部压溃现象。④加载至临界荷载26.7 kN 时，伴随着一声巨响，中支点梁上缘突然断裂，连续梁整体破坏。H92-L～H133-L代表性破坏形态见图4～5。胶合木简支梁、连续梁极限荷载与极限竖向位移的对比结果如表2所示。

表2 极限荷载与极限竖向位移试验结果Table 2 Test results of ultimate load and ultimate vertical displacement

图4 胶合木连续梁破坏形态Fig.4 Failure modes of continuous glulam beams

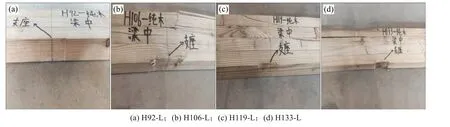
图5 胶合木连续梁在支座处的局部破坏Fig.5 Local failure of continuous glulam beams at the support

在H92-L～H133-L 中，连续梁中支点处上缘会产生较大的负弯矩，致使附近的木纤维薄弱区域、木节处因拉力与剪力的共同作用而产生大量交织裂缝，木纤维断裂明显，结构失效。同时，H92-L～H133-L 中支点处均出现较为严重的局部压溃现象，荷载越大压溃越明显，致使连续梁在试验加载后期，梁中支点处的有效截面面积减少，这也在一定程度上造成了连续梁的脆性受拉破坏。

2.2 荷载-位移曲线

为直接对比2种梁的测试结果，将单跨简支梁对应为双跨简支梁，其荷载值与相应的位移值为试验值的2 倍，并将简支梁和连续梁的荷载-跨中竖向位移曲线绘制于图6。

图6 荷载-跨中竖向位移曲线Fig.6 Load-midspan vertical displacement curves

胶合木简支梁的荷载-位移曲线基本上呈线性变化趋势，在后期逐渐表现为非线性，其抗弯刚度在加载后期变化不大，仅出现了略微降低。胶合木连续梁的荷载-位移曲线基本分为2 个阶段：线弹性阶段和弹塑性阶段。连续梁在弹性阶段的初始抗弯刚度明显高于简支梁，但后期随着荷载的增加，连续梁跨中竖向位移增加速率明显加快，梁抗弯刚度有降低趋势；进入弹塑性阶段后，连续梁表现出的非线性行为要明显地不同于简支梁，连续梁的抗弯刚度有明显的降低趋势，较简支梁更为明显。在相同荷载作用下，胶合木连续梁在跨中所产生的竖向位移要显著小于简支梁。破坏时连续梁极限位移较简支梁降低7.41%～24.37%，极限承载力提升10.47%～22.48%，这表明连续梁的整体抗弯刚度要显著优于简支梁。

由于胶合木梁的弹性模量、跨高比均相同，可以看到截面高度对2 类梁的抗弯刚度影响不大，但梁的极限承载力和极限位移与截面高度呈正相关：简支梁破坏时H133-J 极限位移较H92-J 增加73.21%，极限承载力提升43.12%；连续梁破坏时H133-L极限位移较H92-L增加112.07%，极限承载力提升30.71%。

2.3 截面应变分布

图7 给出了试验梁控制截面的沿截面高度-应变曲线(以H92-J 和H92-L 为例)。由图可知，整个加载过程中，试验梁应变沿梁高基本满足线性变化规律，且沿中性轴上下对称分布。接近极限时，木材应变与荷载的关系表现出非线性，试验梁的中性轴向受拉区轻微移动，但无太大波动。因此胶合木简支梁、连续梁的应变分布情况基本满足平截面假定，可以利用平截面假定对其计算分析。

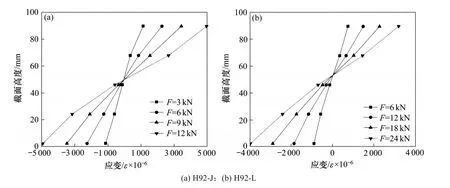
图7 沿截面高度-应变曲线Fig.7 Section height-strain curves

3 理论分析

3.1 弯矩-曲率曲线

弯曲曲率作为梁构件截面分析的重要特征参数，其在数学意义上主要表示在竖向荷载作用下，梁构件产生的竖向挠度的2阶微分，从其物理意义上来说，则表示梁构件发生弯曲时，其弯曲半径的倒数。弯矩-曲率分析方法可以很好地分析出胶合木连续梁从受载到破坏的受力过程与刚度变化情况。

对于求解胶合木梁构件截面的理论弯矩-曲率曲线(M-φ曲线)，通常需要采用以下假定：

1) 平截面假定：胶合木梁从初始受力状态到破坏状态的全过程中，梁截面应变始终符合截面假定。

2) 静力平衡：胶合木梁截面受压区的合力C等于受拉区的合力T，另外压力、拉力乘以力臂与外荷载的弯矩平衡。

3)梁构件的σ-ε关系：胶合木梁截面上只产生分布的正应力，并假设木纤维的σ-ε关系相同，不考虑在受压区沿截面高度的应变梯度、尺寸效应的影响。

4)忽略梁构件剪力的影响。

5) 忽略时间、温度、湿度变化引起的构件应力与应变的变化。

以试验梁控制截面为例，探讨胶合木梁截面的理论弯矩-曲率全过程曲线的获得过程，图8为试验梁控制截面的剖面图。

图8 试验梁剖面图与应变剖面图Fig.8 Profile of specimen and strain

1) 通过试验梁底部测得的平均应变εt,i除以相应的加载阶段下受拉区高度yi，得到该受力状态下的截面曲率φ：

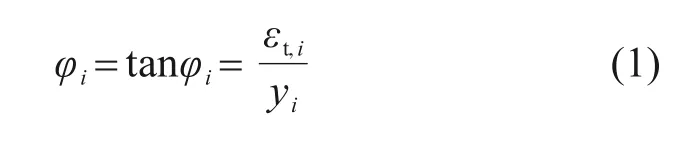
2)分别由胶合木材料的σ-ε关系，获得各条带的应力σ，即：

由胶合木上部受压区各条带分别对中性轴取矩：

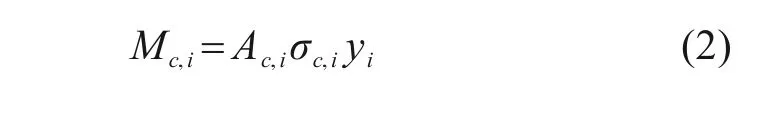
由胶合木下部受压区各条带分别对中性轴取矩：

3)计算试验梁跨中截面的总力矩，即：

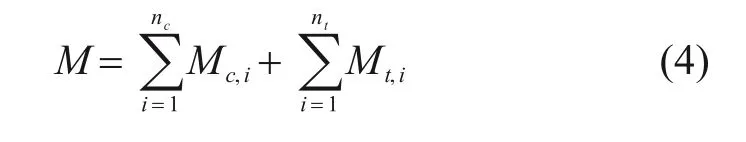
4) 根据每一级荷载所对应的截面曲率，重复利用上述计算过程，获得试验梁跨中截面的理论弯矩-曲率曲线。

通过上述理论计算方法，分别计算胶合木简支梁、连续梁的理论弯矩-曲率曲线，并与试验所得的弯矩-曲率曲线进行了对比(见图9)。从图可知，8 组试验梁的理论计算值相较于试验计算值偏大，但两者能保持较好的符合程度。8 组试验梁的弯矩-曲率曲线的变化趋势显示：梁的弯矩-曲率曲线一直处于上升阶段，胶合木连续梁的弯矩-曲率曲线斜率明显大于简支梁，这表明当截面弯曲曲率相同时，胶合木连续梁所承受的截面弯矩高于简支梁，同时也说明相同变形条件下胶合木连续梁所承受的截面弯矩更大，刚度更大，抗弯性能更好。

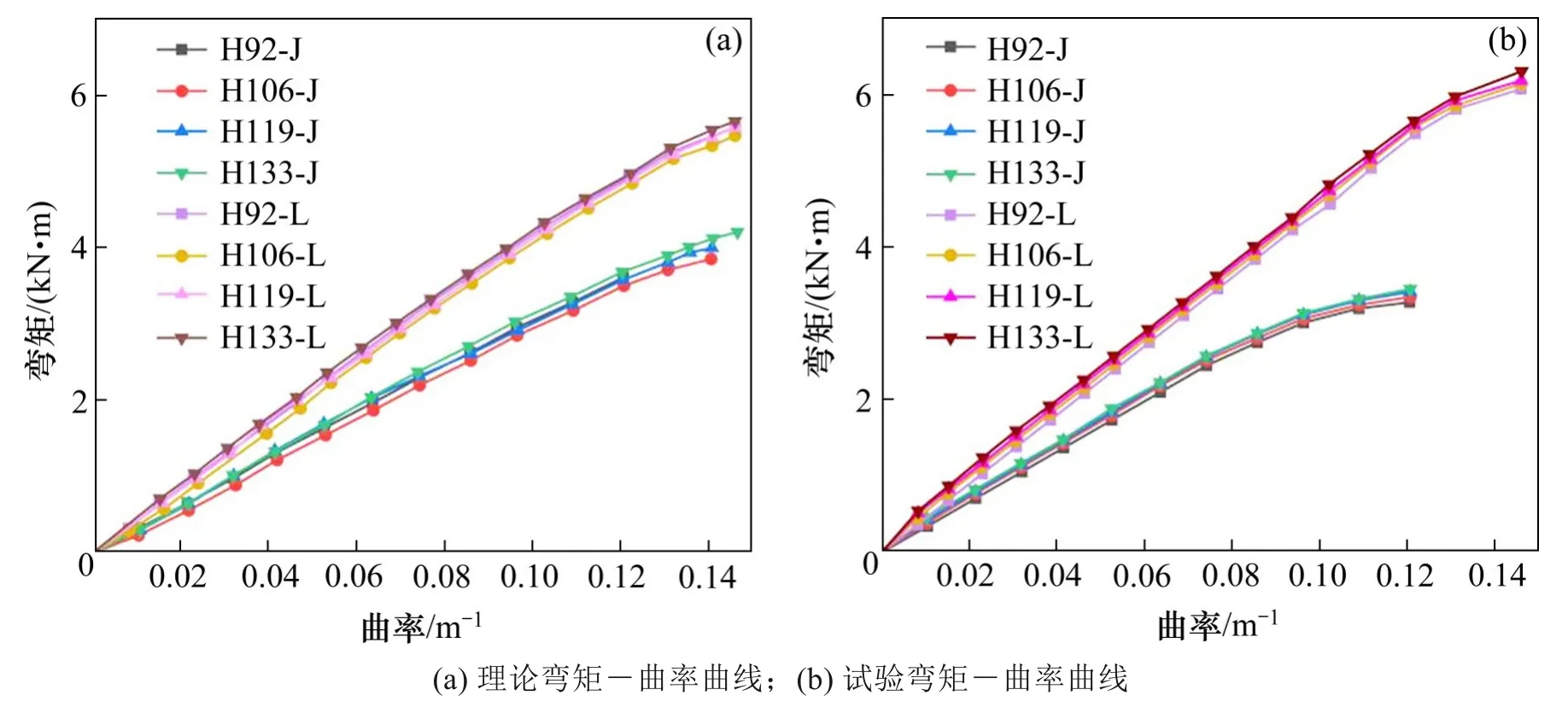
图9 弯矩-曲率曲线Fig.9 Moment-curvature curves

3.2 跨中挠度计算

在胶合木连续梁变形性能分析时，对其2跨跨中截面处的竖向挠度分析计算是一项重要的评判指标。采用弹性理论对胶合木梁进行结构设计，胶合木简支梁、连续梁的跨中挠度分别按下式计算：

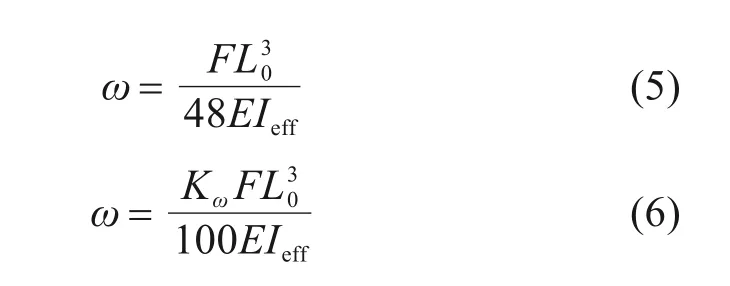
式中：F为集中荷载；L0为计算跨径；E为胶合木梁弹性模量；I为胶合木梁惯性矩；EIeff为试验梁的理论弯曲刚度；Kω为计算系数，当连续梁为2跨连续梁时，Kω取0.911。

计算结果如表3所示。从表中可以看出，胶合木连续梁、简支梁的跨中挠度计算值与试验值吻合较好。连续梁的计算值小于试验值，为胶合木连续梁的结构设计预留了一定的冗余度。

表3 胶合木梁挠度理论值与实测值对比结果Table 3 Comparison results between theoretical and measured deflection values of glulam beams

4 结论

1) 在跨中集中荷载作用下，胶合木连续梁极限位移较简支梁降低了7.41%～24.37%，极限承载力提升了10.47%～22.48%。胶合木连续梁破坏时中支点负弯矩区梁顶受拉破坏，同时梁底与支座接触处局部受压破坏，而简支梁仅跨中受拉破坏，导致结构失效。

2)胶合木连续梁的荷载-位移曲线分为线弹性阶段和弹塑性阶段，胶合木连续梁在线弹性阶段的整体抗弯刚度明显大于胶合木简支梁。而进入弹塑性阶段后，连续梁抗弯刚度降低趋势比简支梁更为明显。

3) 在相同变形条件下，胶合木连续梁较简支梁所承受的截面弯矩更大，刚度更高，抗弯性能更好。采用连续梁结构有望实现胶合木梁跨度的飞跃。