四线临海隧道开挖渗流演变及参数影响分析

任世林

(中国铁建投资集团有限公司，山东 青岛 266000)

青岛地处黄海之滨，地下水丰富，而水是影响工程质量安全的重要因素。水会使边坡安全系数逐渐降低并趋于稳定[1]，同时通过对北京地区7条地铁进行实地调研，结果表明地下水渗漏导致了大部分的隧道病害，约占所有病害的77%[2]。处于地下水位以下的隧道，其内外存在较大的水头差，很容易出现渗漏病害。隧道渗漏会造成地面沉降以及隧道变形，其中后者还可能引起衬砌错位、管片自身产生裂纹等，而这些病害的出现会使地下水渗漏问题更加突出，从而形成一种恶性循环。因此，研究隧道开挖过程中渗流规律及渗流场的演变具有重要的意义。同时可为相似工程条件下隧道渗漏病害的预测与防治提供一定的借鉴与参考。早在1856年，Darcy就通过一系列的水力试验归纳总结了水流在介质中的流动规律，随后渗流微分方程被Zhukovski 创立，渗流理论基础就此奠定。1910年有限差分法由英国学者理査森首次提出，为分析求解渗流场提供了数值法这一种新方法。随着研究的不断深入，1975年CLOSMAN[3]首次总结出三重介质渗流模型；为了解决存在自由面的渗流问题，1973年NEUMAN[4]通过固定网格的Galerkin方法，继而开创了有限元法。近些年，伴随着研究方法及分析技术的发展，国内外学者在一系列已有理论研究的基础上，对隧道渗流问题提出了新的观点与理论，并在众多工程实际中得到了应用[5-8]。其中，在理论分析方面，KOLYMBAS 等[9-10]考虑了不同的边界条件以及控制方程，借助保角变换法得到了圆形断面隧道的涌水量解析解；任文峰[11]则引入复变函数理论，推导了岩溶地层隧道围岩的水压分布与地下水渗流场分布的计算表达式，但这依旧仅仅考虑了隧洞的开挖对围岩原有的水力平衡产生的影响，而未将隧洞的衬砌纳入研究范畴。此后，李杰等[12]在分析水下毛洞任意形状隧道渗流场问题时，研究了注浆圈以及衬砌2 个因素同时作用下渗流场的解；除此之外，还有研究发现，初支、注浆圈以及二次衬砌对水压力、渗流量具有明显的影响作用[13]，本文在此基础上，进一步深入考虑隧洞的开挖以及后期的衬砌综合作用，研究高含水率下的临海隧道渗流场产生的影响效应。此外，数值模拟作为岩土工程研究的重要手段之一，在近些年的工程建设以及科学研究中都起到了重要的作用。其中，LⅠ等[14]在对一段高速公路连拱隧道围岩位移进行研究的过程中，借助FLAC3D有限差分程序发现了考虑渗流的拱顶沉降值要大于不考虑渗流时的沉降；周太全等[15]也应用Abaqus 有限元软件模拟了海底隧道开挖和衬护结构的施作，从而探究了渗流场与应力场之间的相互作用。除此之外，还有大量研究借助了有限元MⅠDAS[16]、ADⅠNA[17]和离散元3DEC[18]、PFC[19]等软件在不同工程背景下，对隧道沉降、围岩应力以及渗流场变化进行模拟计算，也取得了丰富的研究成果。因此，本文也借助Abaqus 有限元计算程序，对隧道开挖及衬砌施作过程中，临海隧道围岩中的渗流场变化展开了数值模拟计算，意图通过模拟高含水率下的隧洞围岩渗流场演化过程，总结隧道施工过程中各项参数对围岩流场产生的作用效应。综合之前学者的研究成果，发现主要是通过理论推导或者数值模拟2种方法对隧道渗流问题进行分析，但对于隧道开挖全过程的渗流场演变特征少有研究。因此，本文根据青岛地铁工程实际，基于Abaqus 有限元软件建立隧道开挖模型，分析对比渗流场的演变特征。同时探究注浆圈厚度以及注浆圈渗透系数对渗流场及渗流量的影响，以期对隧道开挖防水提供相关工程参考。

1 渗流场理论基本方程

1.1 渗流场运动方程

求解渗流场运动方程需要借助各力的平衡条件，对于不可压缩的流体，其液体上的力表现为面力和体积力2 类，根据Navier-Stokes 方程列出渗流场运动方程如下：

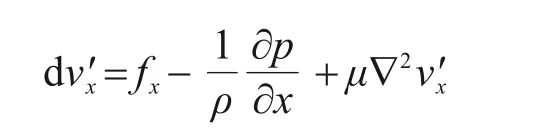
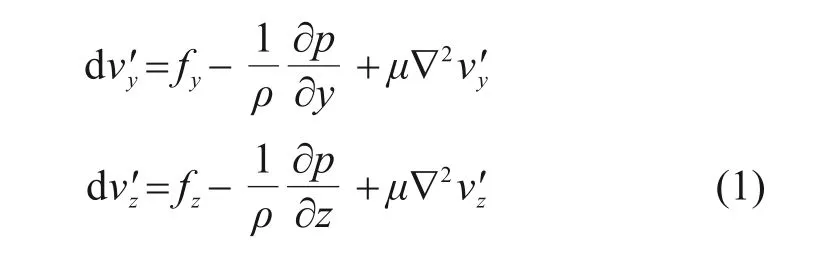
式中：ν′表示孔隙水流的真实速度；p表示液体压强；μ表示液体黏滞度；f表示液体体积力。由于水流的真实速度ν′与全断面孔隙平均流速ν之间的关系可由关系式ν=ν′n表示，因此式(1)可变换为矢量形式：

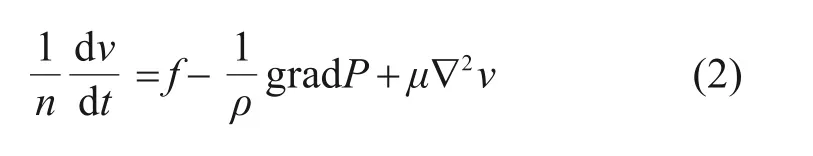
式中：液体体积力f仅包含了沿z方向上的重力，其渗流位势H可以表示为式(3)：

其中：z表示场中某一点的位置高度；p表示该点的压强；γ表示场内液体的容重。若指定单位质量ρ=1，则式(2)可改写为：

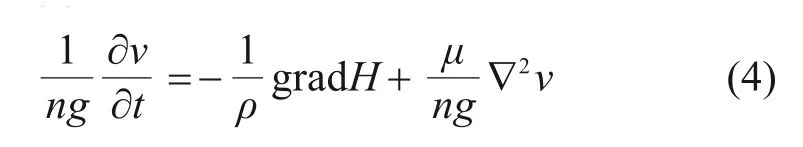
式(4)中的最后一项表示流体经过介质表面时受到的摩擦阻力，而根据沿流程单位长度的能量损失等于单位质量流体渗流阻力的规律，摩擦阻力可由能量损失代替，也就是：

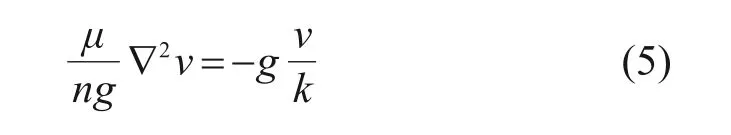
将式(5)代入式(4)，可以得到在多孔隙不变形介质中不可压缩流体的Navier-Stokes方程：

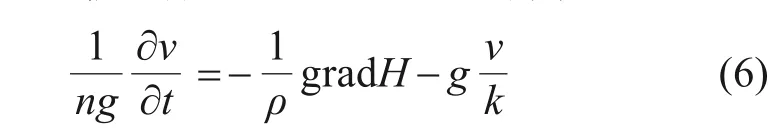
1.2 渗流场连续性方程

在渗流场中取一点P，以P为顶点做一单元六面体，假设此单元体体积dxdydz无穷小，且单元体内的流体可以在介质孔隙中完全通过，如图1所示。

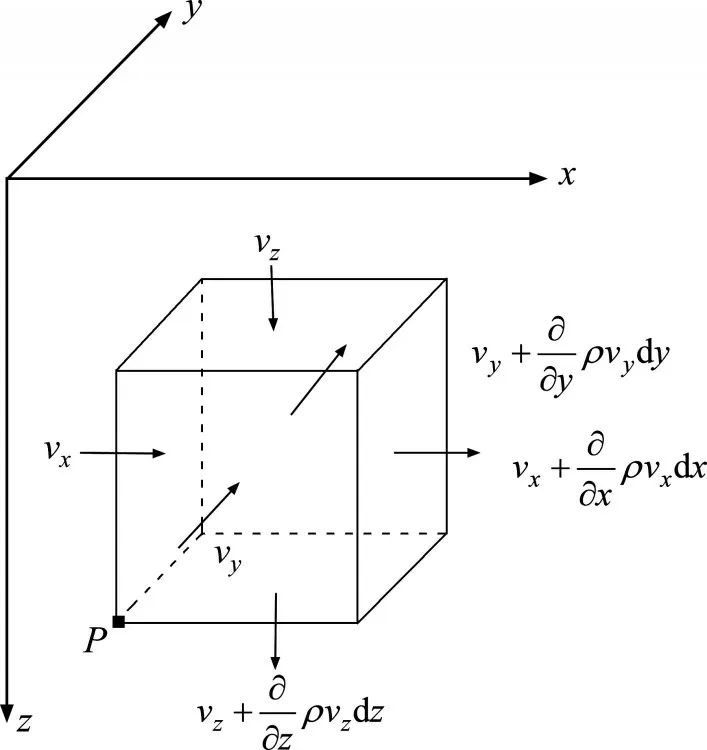
图1 微分单元体渗流模型Fig.1 Differential unit body seepage model

由质量守恒定律可知，流进单元体的液体质量与流出此单元体的液体质量相等[20-21]，因此有：

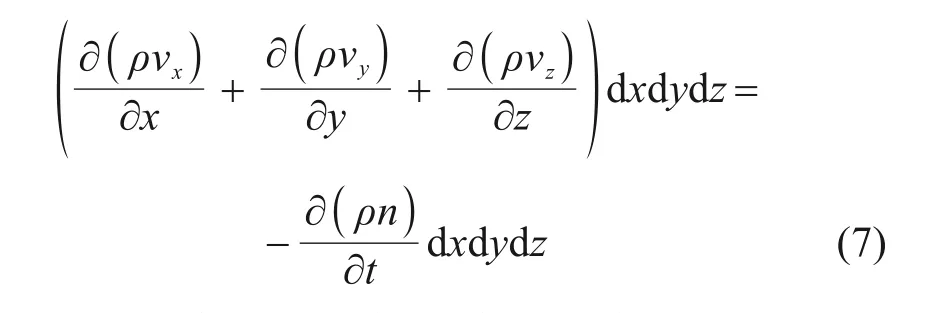
n为孔隙率，如果把水流简化为刚体，即ρ=const，且n不变，则有：

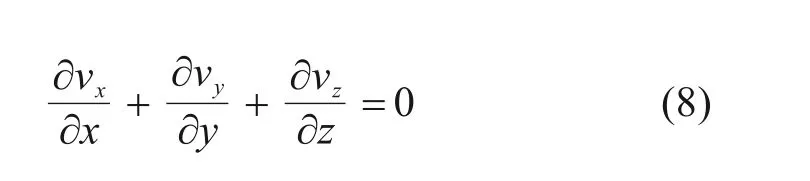
1.3 稳定渗流微分方程

土体中层流状态下水的渗流符合达西规律[22]：

表明层流状态下ν与j成正比，式中ν表示层流状态下流速，j表示水力梯度，而k表示土的渗透系数。不同方向上渗流系数可用矩阵形式表示，因此式(9)可表示为：

将式(10)代入式(8)中，可以得到：

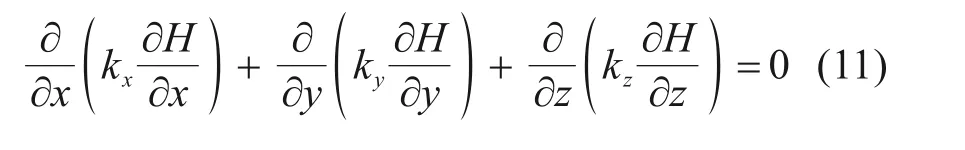
若认为围岩土体是各向同性的，其3个方向上的渗透系数kx=ky=kz,则上式变为：

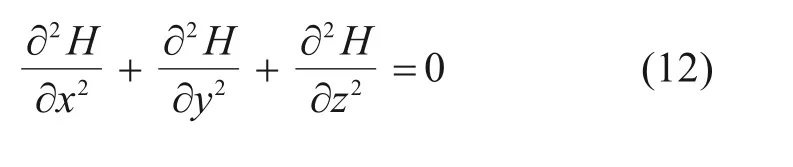
忽略位置z对渗流位势H的影响时，荷载是轴对称的，这是因为水中各点的荷载p来自各个方向。将式(3)代入式(12)得出：

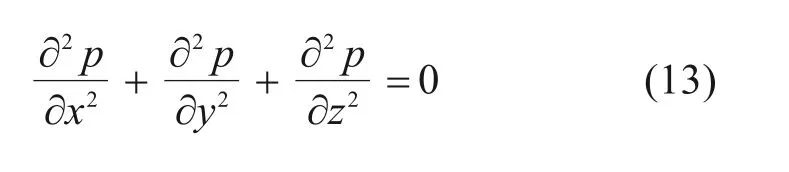
即关于稳定渗流的微分方程。

接下来将基于上述渗流问题理论基础和3类渗流方程，建立青岛地铁水下隧道开挖渗流场计算模型，探究分析大跨度水下隧道开挖过程渗流场的演变特征。

2 隧道渗流场模型建立与开挖模拟

2.1 工程概况

青岛地铁昌乐路站为地下2层岛式站台的暗挖车站，区间分为四线单洞、双线单洞和单线单洞隧道。本文研究对象为四线单洞区，大跨单拱单层结构，宽21.4～22.9 m，区间拱顶埋深在30.8～39.3 m之间，所在岩层主要为微风化花岗岩层。工程所在区域地下水主要为基岩裂隙水和第4系孔隙潜水，地下水稳定水位标高：1.21～11.16 m，稳定水位埋深：1.0～4.90 m。

由于此区间为四线并行，跨度大，为控制沉降采取环形导坑预留核心法的施工方法。即首先开挖拱部，完成锚喷初期支护，然后逐台阶向下开挖至底部，并及时浇筑仰拱及矮边墙，待TBM通过之后，施作剩余侧墙及拱顶的二次衬砌。上下断面的开挖顺序以及隧道横断面图如图2 所示，另外隧道四线单洞区间平面图如图3所示。

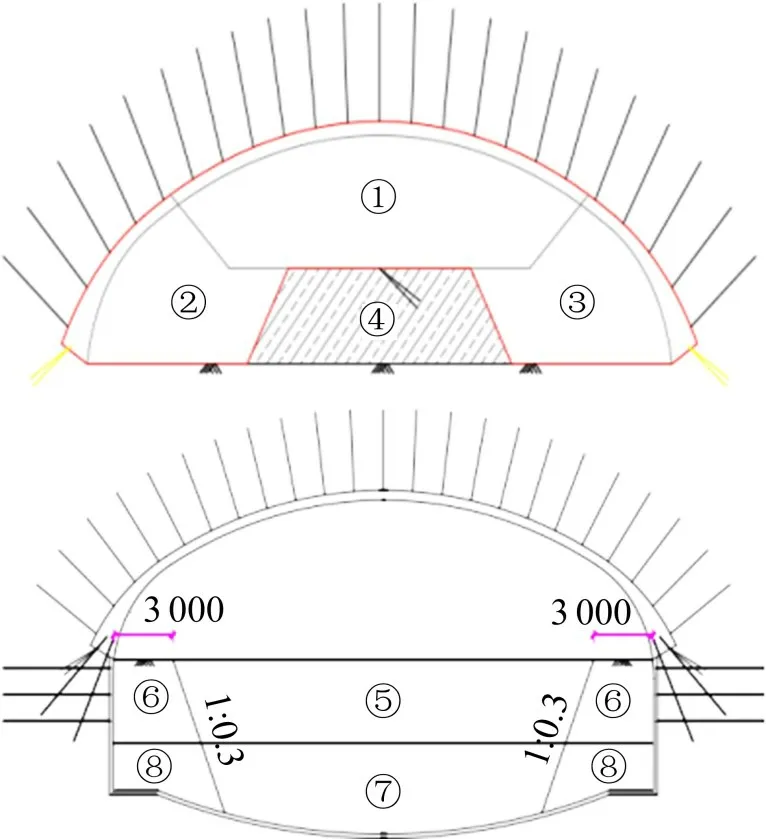
图2 上下断面开挖顺序及隧道横断面Fig.2 Upper and lower section excavation sequence and tunnel cross section diagram

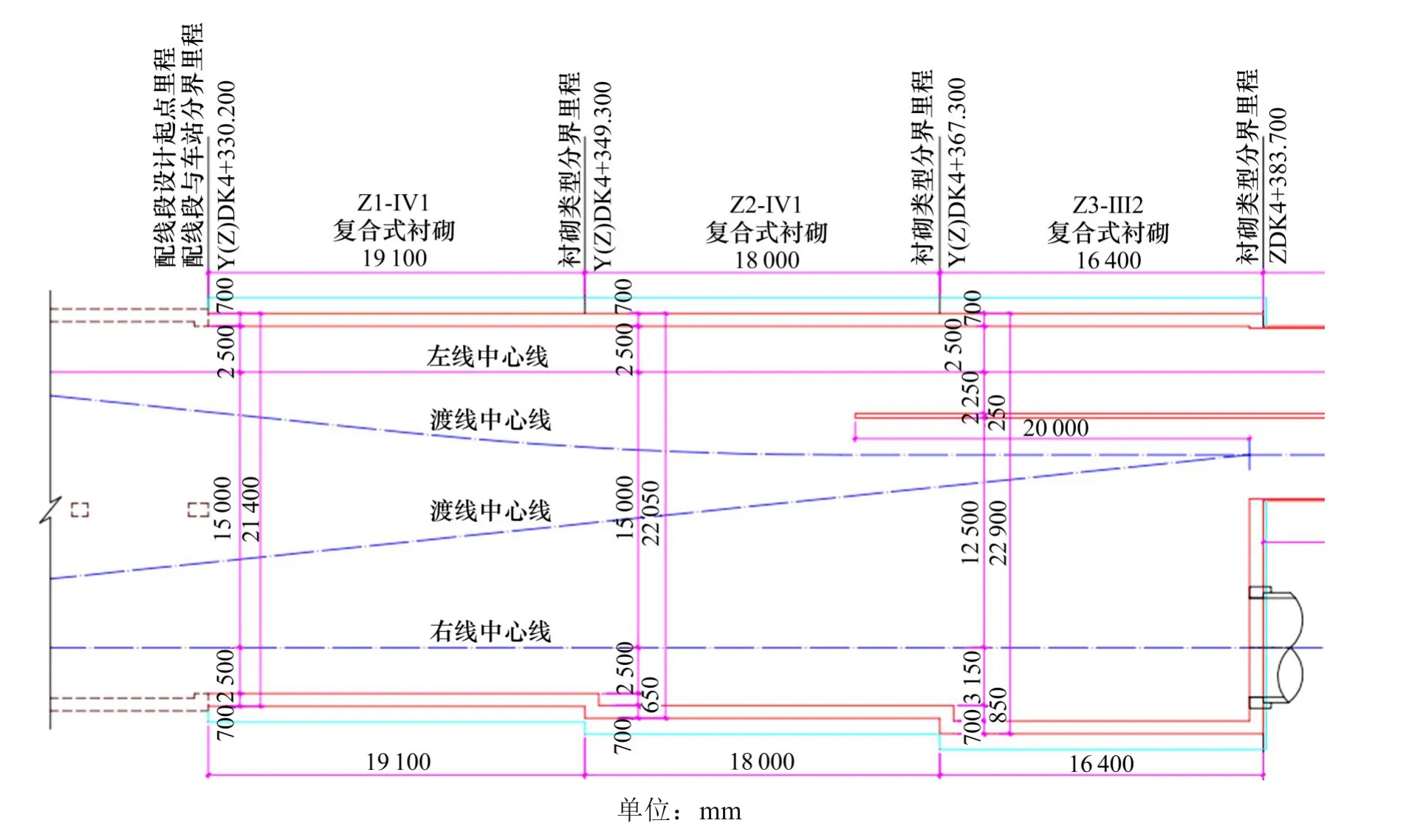
图3 隧道区间平面图Fig.3 Plane map of tunnel interval

2.2 隧道有限元模型建立

本文使用ABAQUS 构建二维平面模型。建立模型的过程中，需要遵循下列基本定律与假定：

1)围岩均质且各向同性，视为连续渗透介质；

2)地下水的流动是连续的，且遵循达西定律；

3)岩体处于稳定渗流状态，地下水水头恒定。

隧道开挖及衬砌施做在实际工程中的程序繁多复杂，为降低模型复杂度，提高计算效率，现对一部分施工步骤和模型做出简化，具体步骤介绍如下。

2.2.1 材料与相关参数

暂时忽略锚杆以及格栅拱架的影响，仅考虑隧道注浆与衬砌的作用，其注浆效果采用注浆圈厚度加以考虑。模型内部围岩、混凝土衬砌等均采用弹性模型。由于本模型仅分析渗流场，暂不考虑围岩应力场，因此力学方面的材料参数对计算结果没有影响，在表1中只给出与渗流相关的必要参数取值。

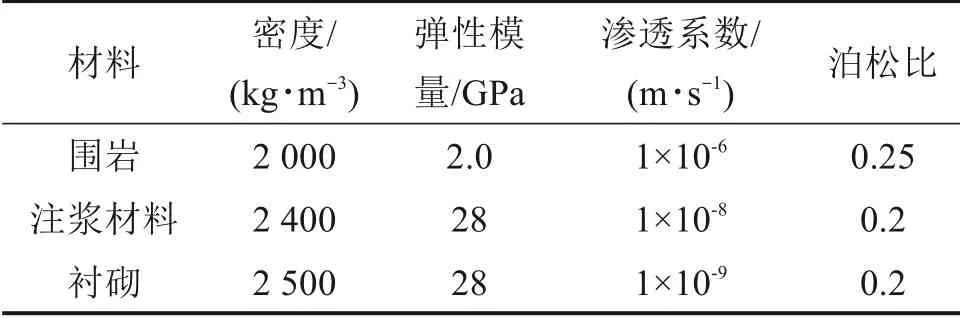
表1 模型参数Table 1 Model parameter

2.2.2 隧道开挖模拟

隧道开挖的实现采用相互作用模块里面的“生死单元”功能，将隧道开挖区域事先选定，在开挖分析步中进行移除。由于本模型暂不分析围岩应力与位移，隧道的开挖过程对渗流计算结果没有影响，为简化模型，本文选择一次性全断面开挖。

2.2.3 荷载与边界条件

为了减少边界效应的影响，整体模型边界长宽取200×200 m，隧道拱顶埋深根据工程实际设置为40 m。在隧道开挖过程中，距离较远的地方其渗流状态变化不大，可以视为处于静水压作用下的稳定状态。考虑水位较高时的不利情况，将地下水水位面设置在模型顶部，即自由面。水的密度为103kg/m3，在重力作用下，模型内部水压从上至下逐渐增大，模型深度为200 m，因此底面处的水压力为2 MPa。对于边界条件：在左右边界控制其水平方向上位移为0，同时保持底面在水平及竖直2个方向上不可移动，顶部为自由面。建立之后的模型如图4所示(红色区域为隧道开挖部分)。

图4 隧道有限元模型Fig.4 Tunnel finite element model

2.2.4 模型验证

模型建立完成后需验证其合理性，此处模型的验证参考江晓洲[17]的计算数据。在注浆圈厚度同为5 m 的情况下，江晓洲[17]的文献中其最大渗流速度约为1.3×10-5m/s。同时，由于其围岩及注浆圈等效渗透系数的取值比本文小了一个数量级，且模型埋深是本文的4 倍，折减后计算结果为3.4×10-5m/s，而本文结果为2.6×10-5m/s，大小相近，表明本文建立的模型具有一定的参考价值。

3 隧道渗流场开挖演变特征对比分析

隧道施工主要分为开挖、注浆、施做衬砌3个部分，本节将按照施工顺序分别对初始状态、毛洞、注浆后以及施作混凝土衬砌后等4种工况进行建模计算，并对其渗流场变化特征进行比较分析。

3.1 初始渗流场

开挖隧道前岩体未收到外界扰动而处于天然状态，此时的渗流场为初始状态渗流场，图5(a)即初始渗流场水压力等值线云图。由图可以看出初始状态渗流场的孔隙水压力分布与静水压力分布是一样的，这是因为隧道周围岩体在原位状态下，地下水处于稳定状态，岩层内部孔隙水压力与静水压力相等。初始状态下渗流场流速矢量图如图5(b)所示，接近于0，进一步说明初始渗流场即为静水场。

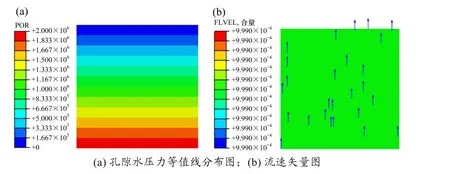
图5 初始渗流场孔隙水压力等值线分布图与流速矢量图Fig.5 Distribution map of pore water pressure contour and velocity vector in initial seepage field

3.2 毛洞渗流场

在初始渗流场模型的基础上把开挖区域内的岩体移除便形成了毛洞渗流场模型。隧洞开挖会产生新的临空面，其上无水压力，可以在边界条件中将隧洞开挖面的孔隙压力数值调整为0以实现模拟。隧道开挖后，周围的地下水在水头差的作用下将会向洞内渗透，破坏原有的渗流平衡，渗流场将重新分布。在静水条件下，孔隙水压力沿深度应成直线分布，开挖后孔隙水压力等值线则会出现弯曲，变水平直线为向隧道中心凹陷的曲线，从而在隧道周围形成降水漏斗，如图6(a)所示。毛洞渗流场流速矢量图如图6(b)所示，图中展示了隧道周边的结果。

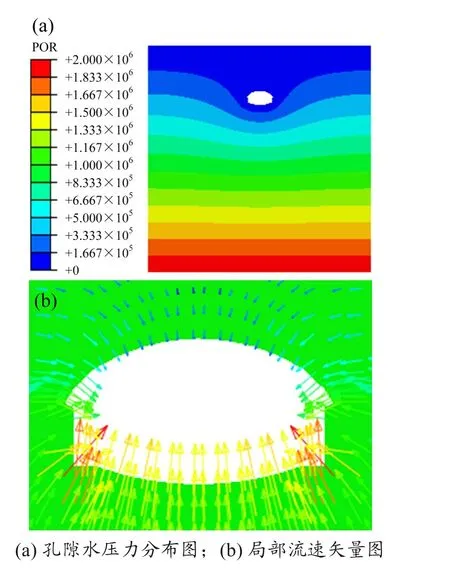
图6 毛洞渗流场孔隙水压力分布图与局部流速矢量图Fig.6 Distribution map of pore water pressure and local velocity vector in capillary seepage field

通过箭头方向可以看出，地下水由四周向隧道中心流动，隧道底部渗流速度大于顶部。流速最大的地方位于隧道两侧拱脚处，流速值约为3.419×10-3m/s。而对于渗流量的计算，可以借助Abaqus 可视化模块中的RVF 这一指标。RVF 的含义为单位时间内进入或者流出模型节点的流体体积，通过对隧道边界节点上的RVF 进行导出并求和便可以得到渗流量，其计算结果约为0.125 m3/s。

3.3 注浆后渗流场

由于隧道围岩中间存在许多裂隙，地下水便通过裂隙从开挖暴露面中渗透出来。从隧道整体稳定和保证施工及维护安全角度出发，一般借助隧道帷幕注浆技术，以减少渗水量。此项技术是指在隧道拱顶、两帮、掌子面等部位，人为开凿一定深度的钻孔，同时把专用浆液以一定压力注入其中，充填进围岩内部的各种孔隙，从而在隧道周围形成一圈混凝土帷幕墙体，通过阻断地下水在孔隙裂缝中的流动，进而达到防水防渗的效果。注浆前后其不同之处在于注浆范围内围岩裂隙被浆液充填，这样浆液凝固后就形成一个坚固的整体，使隧道围岩的渗透性明显下降，大大减轻了渗水现象。

为实现注浆的模拟，现以毛洞渗流模型为基础，在开挖轮廓外5 m 范围重新划定作为注浆区域，通过减小此处区域的渗透系数用以模拟注浆效果，即注浆圈厚度为5 m，注浆圈范围内的渗透系数为1×10-8m/s。另外模型的内外渗流边界条件以及其他参数均与毛洞渗流场的模型相同。注浆后开挖渗流场孔隙水压力等值线分布如图7所示。

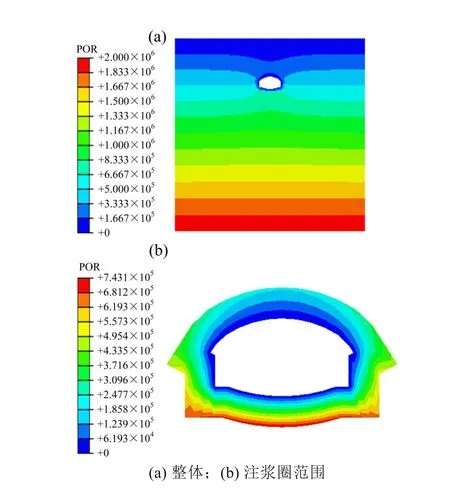
图7 注浆后开挖渗流场孔隙水压力等值线分布图Fig.7 Distribution map of pore water pressure contour in seepage field after grouting

与毛洞渗流场孔隙水压力等值线分布图相比，图7(a)所示的注浆后整体孔隙水压力等值线明显变得平滑，弯曲程度大大减小，仅在隧道周边小范围内出现凹陷，其余部分恢复为初始渗流场时的静水压力。对比前后2种情况能够说明通过对隧道周围岩体进行注浆，孔隙水压力分布有了显著变化，地下水的渗流情况改善可观。而由图7(b)能够观察到，注浆圈最内侧为开挖暴露面，孔隙水压力为0，并沿着径向逐步增大到0.75 MPa，与静水压力相衔接。

为突出注浆效果，下面仅给出隧道周围的云图结果。其中图8 为注浆后注浆圈部分流速矢量图，图9为注浆后注浆圈部分渗流量云图。与毛洞渗流场相比较，注浆开挖后隧道周围地下水的流速有了明显的减小，注浆区域渗流速度最小仅为2.6×10-5m/s 左右。其箭头指向隧道内部，表明地下水仍是由四周向隧道中心流动。同理通过对图9开挖面上节点的RVF 数据进行导出并求和，得出渗流量约为0.006 m3/s，约为毛洞渗流量0.125 m3/s的1/20，渗流量大幅减少。且可以看出，渗流量最大的地方位于隧道两侧拱脚处，为5.73×10-4m3/s。

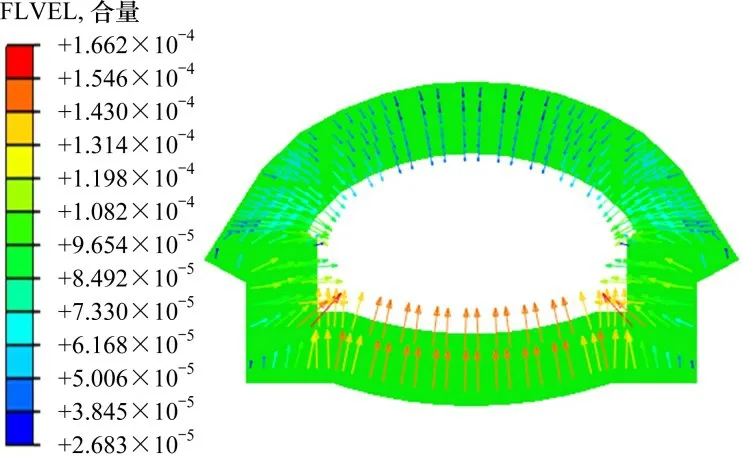
图8 注浆圈区域流速矢量图Fig.8 Velocity vector diagram of grouting circle area

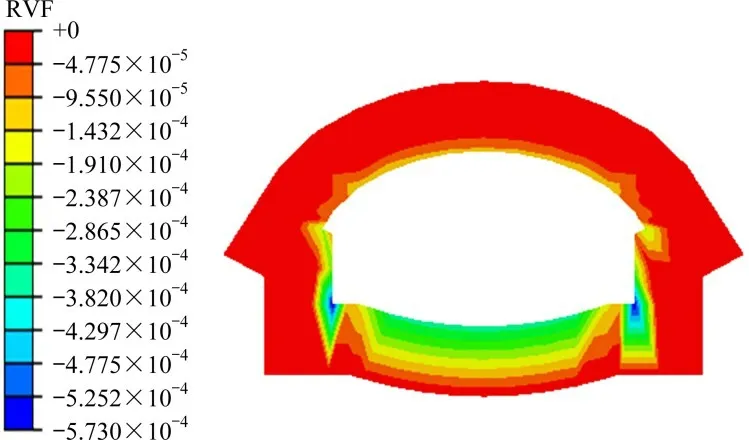
图9 注浆圈区域渗流量云图Fig.9 Cloud map of seepage flow in grouting circle area

3.4 施做衬砌后渗流场

为了保护围岩的稳定性，防止围岩变形或坍塌，隧道采取强度足够的衬砌来确保施工及行车安全。隧道衬砌是沿隧道洞身周边用钢筋混凝土等材料修建的永久性支护结构，不同的围岩中可采用不同的衬砌形式，常用的衬砌形式有喷混凝土衬砌、喷锚衬砌及复合式衬砌。地下水丰富的地区，衬砌兼有防水抗渗的功能。

本模型将依据设计图纸进行衬砌的建模，为方便计算，忽略衬砌中的钢拱架结构。以注浆后开挖隧道模型为基础，在隧道开挖面内部创建一圈块体用以模拟衬砌，如图10 中红色区域所示。设置衬砌的渗透系数为1×10-9m/s，模型内外渗流边界条件以及其他参数均与之前模型相同。

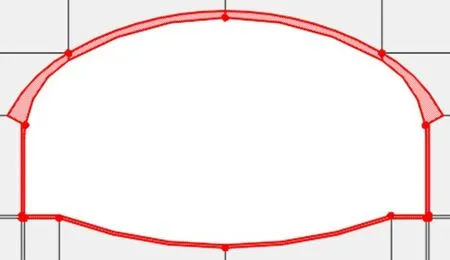
图10 隧道衬砌局部放大图Fig.10 Local magnification map of tunnel lining

施作衬砌后可得隧道渗流场孔隙水压力等值线分布图11，对比图7(a)和图11(a)的云图结果可以看出，在施作衬砌前后，渗流场并没有产生明显的改变，对渗流场的影响范围仍在开挖面以外5 m 左右，即注浆圈厚度范围。其不同之处则由局部放大部件云图可以得知：在衬砌范围内，孔隙水压力由0最大变化到0.24 MPa左右；在注浆圈范围内，由于衬砌的存在注浆圈没有暴露面，因此孔隙水压力最小不再为0，而是沿着径向从0.09 MPa 逐步增加到0.75 MPa，并最终于静水压力相衔接。

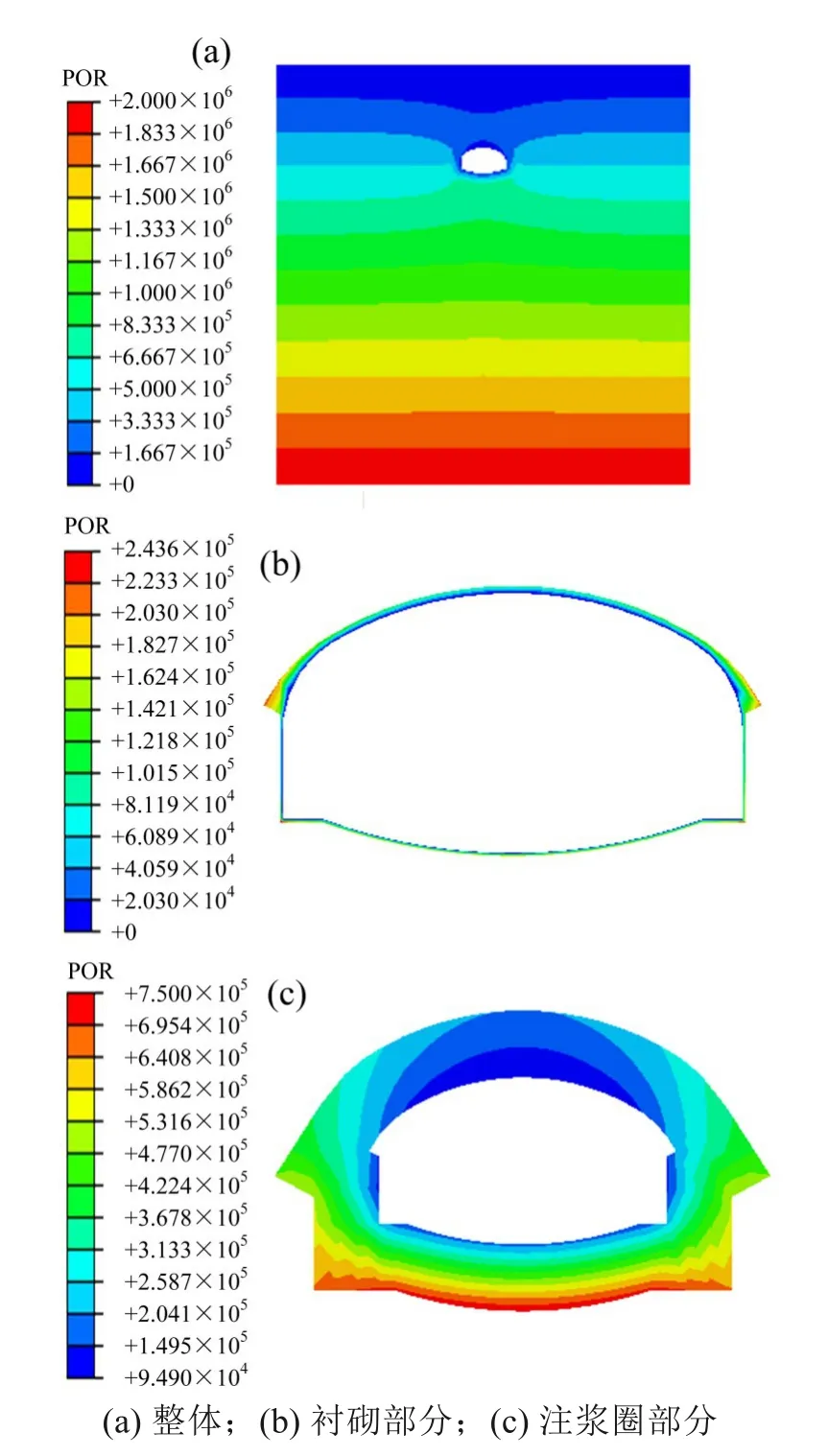
图11 施做衬砌后开挖渗流场孔隙水压力等值线分布图Fig.11 Distribution of pore water pressure contour in seepage field after lining construction

施作衬砌后隧道周围注浆圈区域流速矢量图如图12 所示，可以看到其地下水的流动趋势基本未发生变化，仍是趋向于隧道中心流动，但注浆区域流速有所减小，最小仅为1.8×10-5m/s。图13为施做衬砌后衬砌部分渗流量云图，其渗流量分布与之前相似，主要分布在衬砌两侧与底部，最大渗流量约为3×10-4m3/s。将开挖暴露面上节点的RVF 求和后，得到渗流量约为0.002 5 m3/s，约为施做注浆圈后开挖渗流量0.006 m3/s 的40%，渗流量进一步减小。

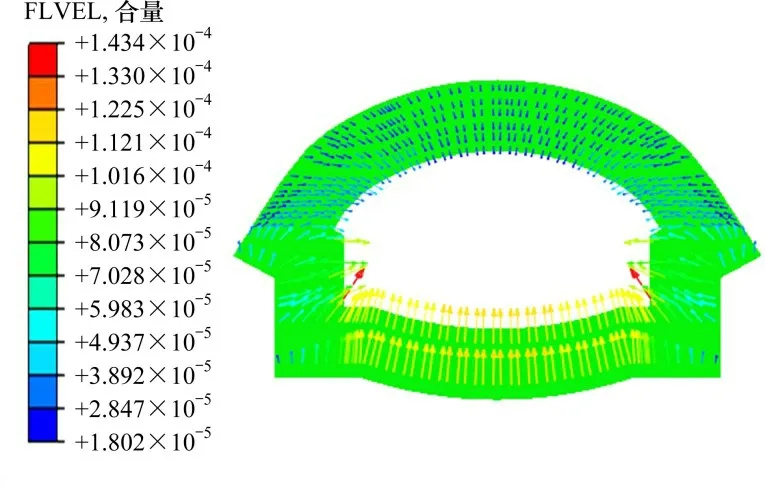
图12 施做衬砌后注浆圈区域流速矢量图Fig.12 Flow velocity vector diagram of grouting circle area after lining construction

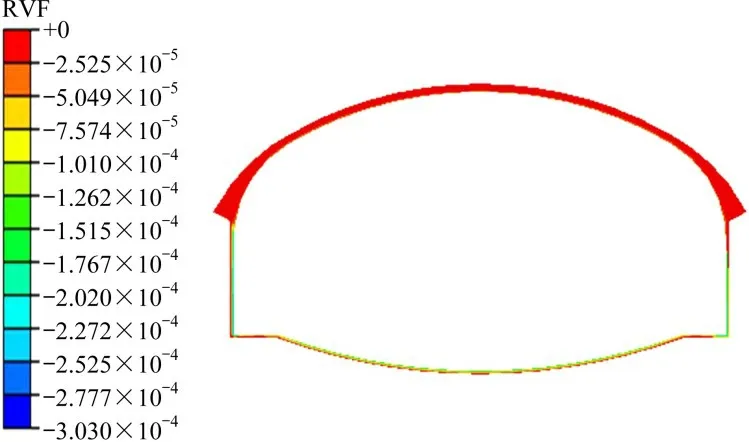
图13 施做衬砌后衬砌区域渗流量云图Fig.13 Cloud map of seepage flow in lining area after lining construction

4 主要参数对隧道开挖渗流场的影响

通过上一节的模拟计算，发现隧道帷幕注浆和施做防水衬砌对渗流场的影响是巨大的，可以有效减少渗流量。为了进一步的研究二者与渗流场、渗流量的关系，本节欲探讨注浆圈厚度和注浆圈等效渗透系数2 个参数对模拟计算结果的影响。

为方便数据分析，更直观地体现出改变参数产生的效果，首先设置几个监测点来记录不同参数下的孔隙水压力值，考虑模型是对称的，仅在一侧布置监测点即可，如图14所示。

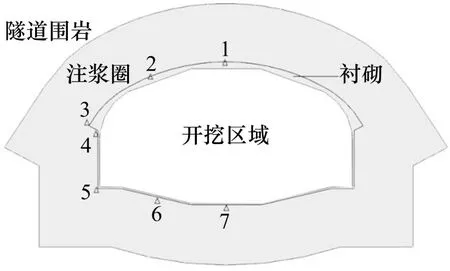
图14 孔隙水压监测点布置图Fig.14 Layout chart of pore water pressure monitoring points

4.1 注浆厚度对开挖渗流场的影响

通过上一节的模拟分析，隧道注浆可以明显改变渗流特征，大幅降低渗流量，是影响渗流场非常关键的因素。一般情况下，注浆厚度越大其防渗效果就会越好，但注浆厚度过大也会造成施工困难以及投资增大。本节主要研究注浆圈厚度对隧道渗流场的影响，在施做衬砌后模型的基础上只需改变模型中注浆圈的厚度，即重新划定注浆区域并设置其渗透系数，其他参数都与之前模型保持一致。注浆圈厚度的分析范围为0～15 m，分别为0，2.5，5，7.5，10 和15 m 共6 个厚度模型，如图15 所示。其中第1 张图片无注浆，灰色区域表示注浆厚度。

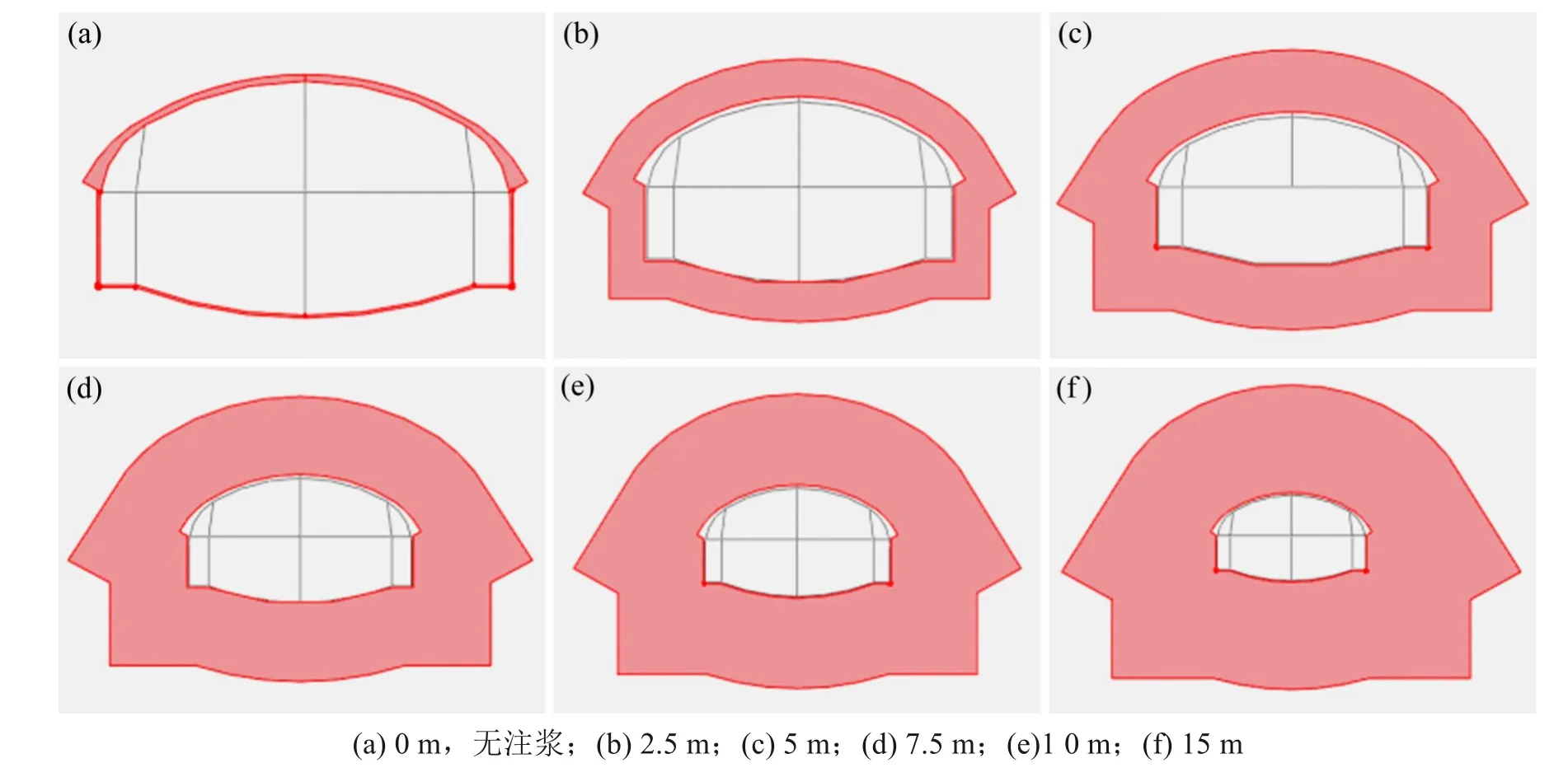
图15 不同注浆圈厚度的计算模型Fig.15 Calculation model of different grouting circle thickness

模型计算完成后绘制图16，由图可以看出注浆圈厚度与孔隙水压力二者成反比关系，孔隙水压力随着注浆厚度的增大而逐步减小，且7个监测点处的变化趋势相同。当注浆厚度从0 增加至7.5 m 时，孔隙水压力减小很快，其变化范围大致为0.5 MPa。而当注浆厚度处于7.5～15 m 之间时，水压力减小幅度远不如前，不足0.1 MPa，在图中表现为孔隙水压力曲线逐渐趋近于一条水平直线。计算结果表明能够明显影响衬砌后孔隙水压力的阶段是注浆厚度处于0～7.5 m 范围内，而超过这个区间进一步增大时，其影响效果是边际降低的。因此为了更好地平衡施工难度、经济效益以及注浆效果等因素，参考本节模拟计算结果可选择5～10 m注浆深度。

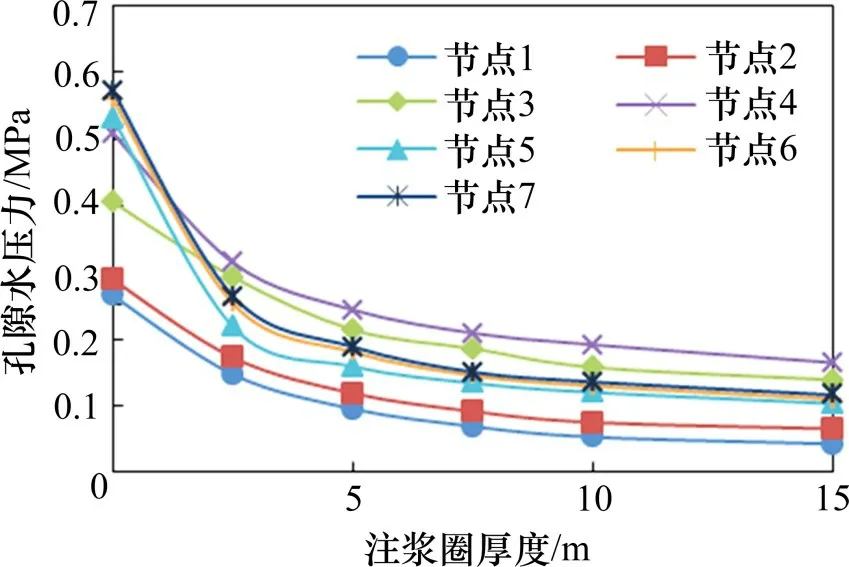
图16 孔隙水压力与注浆圈厚度关系Fig.16 Relationship between pore water pressure and grouting circle thickness

隧道渗水量与注浆圈厚度的关系如图17所示，相比于图16 中孔隙水压力曲线的变化趋势大致相同。隧道渗流量同样与注浆圈厚度成反比，注浆圈厚度越大，其渗流量就越小。当注浆厚度在0～7.5 m 范围内变化时，渗流量明显减少，减少量大约有0.005 m3/s，而当注浆厚度大于7.5 m时，对渗流量影响并不显著，其减少量还不足0.001 m3/s。

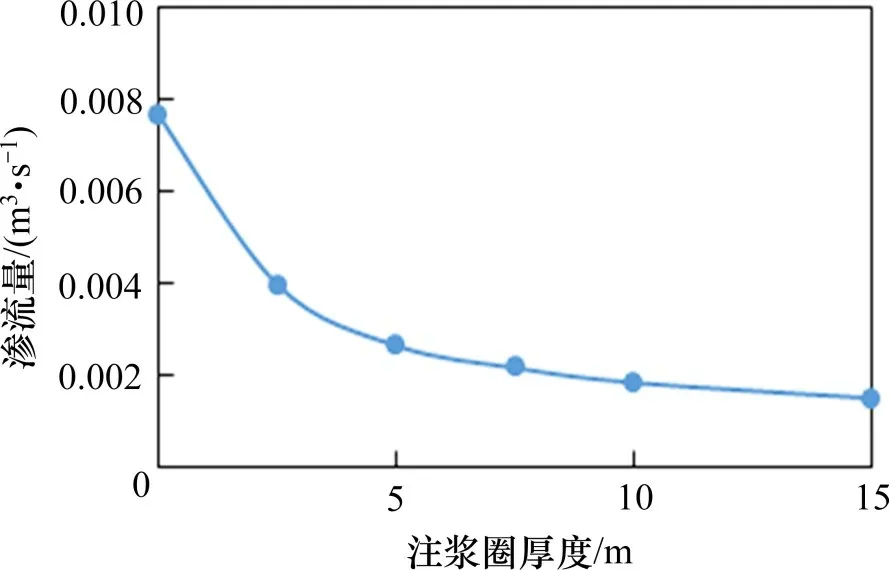
图17 隧道渗水量与注浆圈厚度关系Fig.17 Relationship between tunnel seepage and grouting circle thickness

综上所述，注浆圈厚度是影响隧道渗流场的重要因素，在0～8 m 范围内对衬砌背后孔隙水压力和隧道渗水量有着明显影响，这2个指标在此范围内的变化值能够占到总变化值的4/5。而在8～15 m 区间内，影响效果边际减弱，孔隙水压力及渗水量的变化趋于平缓。通过参考以上结论，可以结合实际情况选择合理的注浆圈厚度。

4.2 注浆圈渗透性对开挖渗流场的影响

有关注浆圈的另一个参数是注浆圈的渗透性，宏观上可表现为注浆材料的选取与注浆压力的确定：注浆材料具有防水性能则注浆圈渗透性低；而注浆压力越大则围岩孔隙填充更密实，注浆圈渗透性亦会降低。此处选取5 m 厚度注浆圈，仅通过改变注浆圈区域的渗透系数来模拟不同渗透性下的注浆效果。其渗透系数大小分别设置为0，1×10-9m/s，1×10-8m/s，5×10-8m/s，1×10-7m/s，2.5×10-7m/s，5×10-7m/s，其余条件同前。

模型计算完成后，提取各监测点孔隙水压力，得到孔隙水压力与注浆圈渗透系数之间的关系如图18 所示。由图可以看出衬砌背后孔隙水压力与注浆圈渗透系数成正比，7 个监测点处孔隙水压力都是随着注浆圈渗透系数的增加而增大。当注浆圈渗透系数处于0～1.0×10-7m/s 范围内，衬砌背后孔隙水压力的变化最为明显，水压力的增加值约为0.2～0.5 MPa。在注浆圈渗透系数超过1.0×10-7m/s 后，孔隙水压力基本不再发生变化，增加值仅有0.1 MPa 左右。综上判断，当注浆圈渗透系数大于1.0×10-7m/s 时，衬砌背后的孔隙水压力较大，建议选择注浆后围岩的渗透系数小于1.0×10-7m/s。

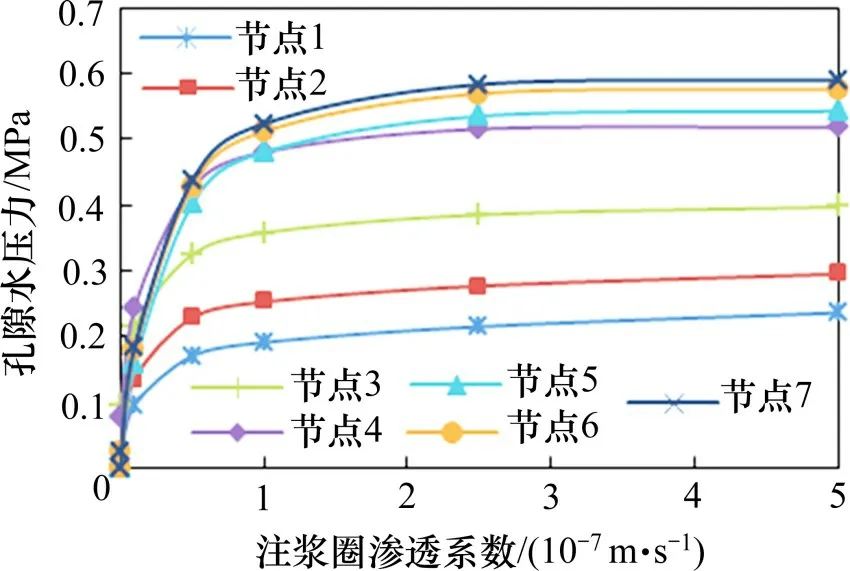
图18 孔隙水压力与注浆圈渗透系数关系Fig.18 Tunnel finite element model

隧道渗水量与注浆圈渗透系数的关系如图19所示，和衬砌背后水压力相比其变化趋势是相同的，注浆圈渗透系数越大，渗水量也随之增加。当注浆圈渗透系数处于0～1.0×10-7m/s之间时，渗水量变化非常明显，而当超过1.0×10-7m/s 之后并直到5.0×10-7m/s，渗水量几乎都不再变化。由此可以说明，当注浆圈渗透系数达到并小于1.0×10-7m/s时，其堵水防渗效果才能更好地发挥出来。

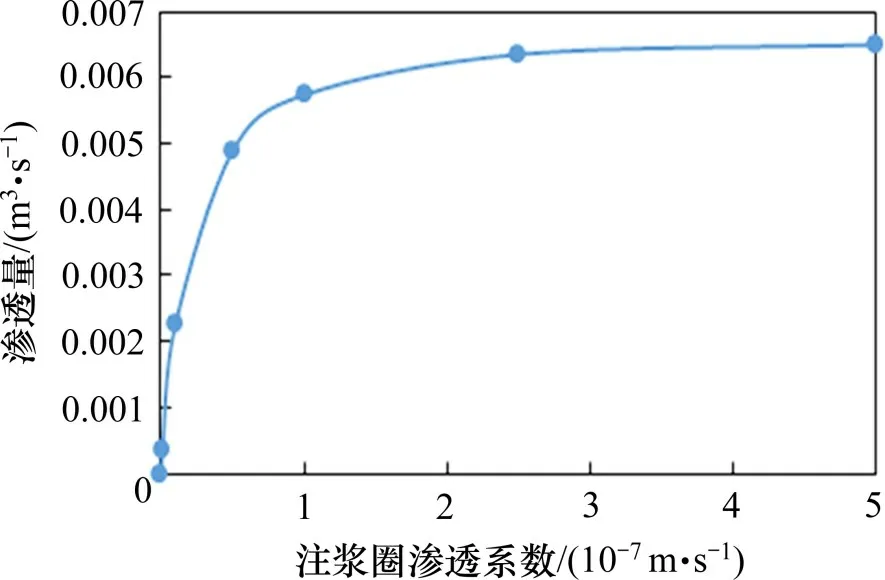
图19 隧道渗水量与注浆圈渗透系数关系Fig.19 Tunnel finite element model

通过计算结果判断得知，影响隧道渗流场的另一关键因素是注浆圈的渗透性，渗透系数在0～1.0×10-7m/s 区间内变化时对孔隙水压力和渗流量的影响是显著的，但是在当系数大于1.0×10-7m/s之后，影响程度就有了明显的减弱。在注浆圈渗透性变化过程中，衬砌背后的孔隙水压力与隧道渗水量的变化趋势基本一致，这与文献[17]结论类似。

5 结论

1) 隧道开挖前，岩体中的渗流场未受开挖影响，保持原始状态即静水场，场中各处孔隙水压力相互平衡，因此流速为0。在未注浆情况下对隧道进行开挖，渗流场会受到强烈影响，临空面的产生使大量地下水流失。注浆后开挖隧道，孔隙水压力等值线明显变得平滑，弯曲程度大大减小，对渗流起到了明显的抑制效果，渗入隧道的水量约为毛洞渗流量的1/20，渗水量大幅减少。施作衬砌后，开挖对渗流场的影响继续减弱，影响范围仅在注浆圈范围，渗入隧道的水量进一步降低，约为注浆后开挖渗流量的2/5。

2) 当注浆圈厚度在0～7.5 m 之间变化时，对衬砌后孔隙水压力影响较为显著，当注浆圈厚度大于7.5 m 后，衬砌后孔隙水压力变化曲线趋于平缓；注浆圈厚度对隧道渗流量大小的影响规律与之相同。

3)注浆圈等效渗透系数从0增加至1.0×10-7m/s时，对衬砌后孔隙水压力和渗水量影响显著，当超过1.0×10-7m/s 后，衬砌后孔隙水压力及渗水量的变化量几乎为0，二者曲线变化趋势相似，先快后慢增大达到上限值并逐渐趋向于水平直线。

4)影响渗流场的关键因素有2个：一是注浆圈的厚度；二是其等效渗透系数。综合考虑施工难度与注浆防水效果，注浆圈厚度可选取为5～10 m，注浆圈渗透系数可控制在1.0×10-7m/s以内。