双洞隧道在断层破碎带的涌水量预测

2022-08-29阮志刚刘宁

铁道科学与工程学报 2022年7期

阮志刚，刘宁

(1. 四川交通职业技术学院，四川成都 611130；2. 贵州大学土木工程学院，贵州贵阳 550025)

在断层破碎带中进行隧道修建，当地下水位较高时，极易导致突涌水害，给施工带来极大安全隐患。所以隧道开挖后的涌水量大小预测，对隧道设计、施工都具有重要的指导意义。有关隧道穿越富水地层的涌水量预测，许多学者曾做过相关研究。郭熹等[1-3]利用统计学和神经网络等方法通过对多个隧道涌水案例进行分析和评估，总结了诱导涌水发生的原因和主要风险源，但这类基于数据驱动的方法需要大量的样本作为支撑，且对突涌水害无法进行机理性的解释。王建秀等[4]认为对隧道的涌水量计算要结合隧道预设计阶段的正演和隧道施工监测阶段的反演方法；为了得到隧道在地下排水量的解析解，GOODMAN等[5]使用图像法将隧道视为排水井，并推导了涌水的经典解析解；后来EL 等[6-7]又发展了基于保角变换的隧道涌水量计算方法。目前，隧道在普通地层的涌水量计算方法已经成熟，所以，目前的研究重点更多集中于软弱或破碎地层。王鹏飞等[8]通过试验的手段，研究了存在于断层区域不同含石率的土体试样的渗透系数；李廷春等[9]考虑到裂隙岩体中的渗流可能导致颗粒介质的损失，运用流固耦合理论分析了隧道穿越富水断层带的突水过程；师文豪等[10]也通过有限元的方法模拟了矿山巷道在遇到破碎岩体时突水的演化过程；ZHANG 等[11]则分析了隧道在遭遇断层面临突水时的地下水头分布情况，发现隧道越接断层，水头线越发密集，这也说明隧道对隧道的突水有明显的促进作用；针对在实际工程中面临的掌子面突涌水，HWANG 等[12]利用图像叠加法对隧道揭露倾斜含水层时掌子面的涌水量进行了理论求解；朱彬彬等[13]在渗流微分方程的基础上，提出了隧道在富水断层控水模型中的涌水量公式。以上研究大多建立在隧道在普通围岩条件下的水害分析，或者单洞隧道在断层破碎带区域的涌水量计算，而双洞隧道揭露断层时的涌水量预测较少，所以本文通过对断层影响宽度的分析和计算，对断层区域进行分区，并利用非达西修正和叠加原理，建立双洞隧道在断层不同区域的涌水量计算模型，提出了相应的计算方法。

1 隧道与断层的等效距离

在普通围岩中，地下水向隧道内流动形成地下水降落漏斗，该漏斗的影响半径为R，一般与岩土层的渗透性能、地下水补给边界有关，根据《铁路工程水文地质勘察规程》，该影响半径R为：

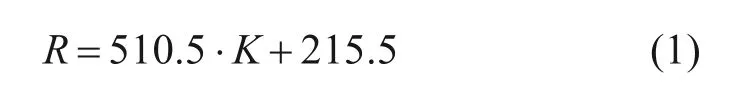
从上式可知，隧道引起的渗流场变化范围主要与地层的渗透系数K有关。可在实际施工中，山岭隧道会遇到地下构造发育的地带，例如断层构造。当隧道靠近断层区域，地下水降落漏斗影响半径则会受到由于断层形成的地下水侧向补给边界的影响，此时地下水流线和等水头面往往会与无限含水层中的渗流情况不同。

为判断断层是否会对隧道附近的渗流场产生影响，首先需要对隧道与断层的位置关系进行分析[13]。当隧道遭遇断层时，隧道与断层的几何关系如图1所示。

在图1 建立的几何模型中，y为代表隧道轴线方向，以隧道开挖方向为正，在y方向上，掌子面与断层的距离为s；在水平面垂直隧道的方向，掌子面与断层的距离为x的绝对值；η为断层面的倾角；ω为隧道轴线与断层走向的夹角。

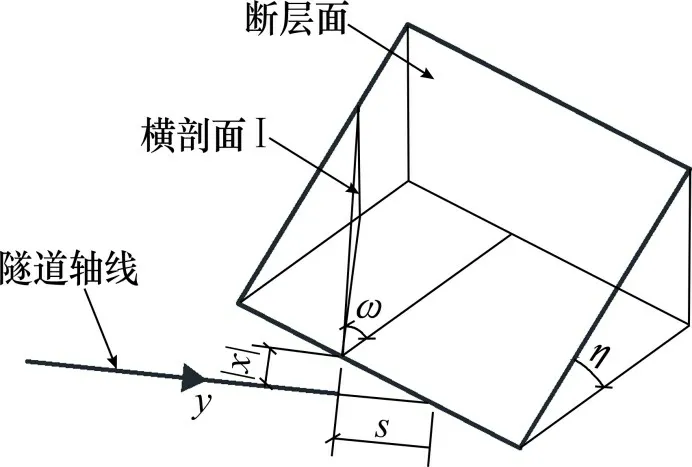
图1 隧道与断层的三维几何关系图Fig.1 Three dimensional geometric relationship between tunnel and fault

为简化计算，本文参考文献[13]和[16]，将隧道遭遇断层的三维涌水问题转化为二维，即将横断面内的原始倾斜断层等效为垂直断层。其中，文献[13]基于安全考虑将断面内隧道与断层的最小距离，即垂直距离视为隧道与等效垂直断层间的等效距离，但当断层倾角很小时，该等效方式与实际差距较大，另外，文献[16]将横断面内隧道轴线到断层的水平距离作为等效距离a，且在不同断层倾角的工况下进行了倾斜断层模型和垂直断层模型的涌水量模拟计算对比，证明了该等效方式的可行性，因此本文也将参考此等效方式。

2 断层影响分区

文献[14]根据断层案例的现场量测及数据统计分析，研究了不同类型断层的节理发育规律，将断层由中心地带向两侧垂直方向进行了分区，包括位于断层中心地带的断层破碎区Ⅰ，以及中心地带两侧局部破碎但未丧失强度的岩体地带，即断层影响区Ⅱ，还有距离断层较远，受断层影响较小的普通岩体区Ⅲ，其中，断层影响宽度范围包括Ⅰ区和Ⅱ区，并得到了断层影响宽度范围的经验公式。本文为研究断层对地下水涌入隧道而形成的渗流场的影响，以叠加原理为基础，提出另一种断层影响宽度的计算思路。

当隧道在普通围岩中，没有断层的影响，可以假定其处于半无限含水层中，隧道开挖后，地下水流动可视为潜水运动，该渗流模型如图2所示。

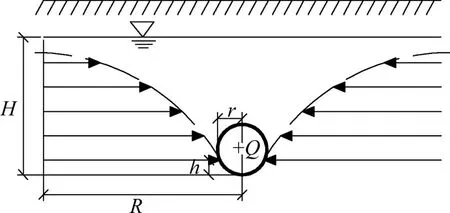
图2 地下水潜水运动渗流模型Fig.2 Seepage model of groundwater movement

此时，引入裘布依微分方程式，并根据模型设定边界条件，如下式所示。

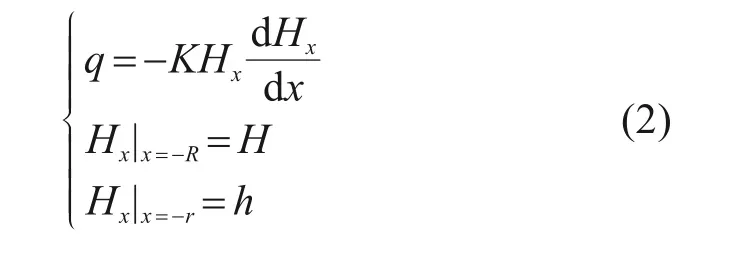
其中：R为半无限含水层中地层的渗流影响半径；r为隧道半径；H为地下水初始水位；h为隧道内水位高度。则可得到隧道的一侧的涌水量。

在图2模型中，左右两侧对称，则隧道在普通岩体区的单位长度出水量为：

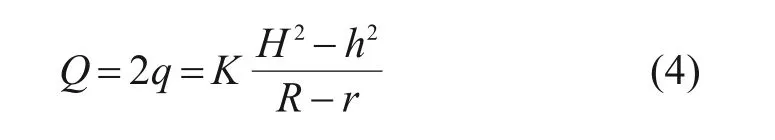
值得注意的是，由式(2)推导的隧道出水量适用于潜水条件，而当实际中隧道可能会遭遇承压水地层，此时需将式(3)或式(4)中的(H2-h2)/2 替换为(H-h)·M，其中M为含水层厚度[17]，本文后续推导均可通过该方式将潜水条件下转换为承压水条件下的地下渗流。

而当隧道断面处于断层影响范围内时，断层构造衍生的节理裂隙，会加速水流速度，使其衍变为非达西渗流，文献[15]通过对渗透系数的修正表征了次影响，如式(5)所示。

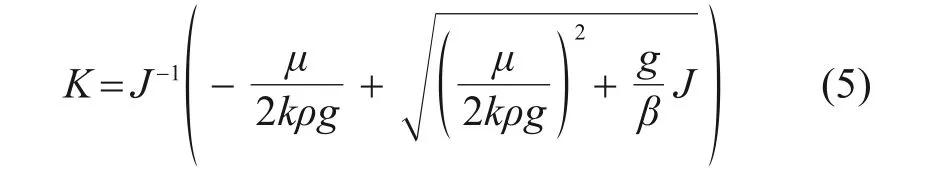
其中：μ为液体的动力黏滞系数，Pa·s；k为岩土体的渗透率，m2，为表征岩层渗透性能的常数，仅取决于岩石的性质，而与液体的性质无关；ρ为液体的密度，kg/m3；β为非达西流影响系数，m-1；g为重力加速度，m/s2。

此外，断层对渗流场的影响还表现在其切断了半无限含水层，构成地下水渗流的补给边界[16]。为此，此处采用镜像叠加的原理将断层边界的影响用虚拟隧道来代替，从而把有限的渗流区化为虚构的无限渗流区，但要求仍保持原有的其他边界条件和水流状态。利用叠加原理，可求得原问题的解。模型示意图如图3所示。

图3 断层影响区内隧道镜像示意图Fig.3 Schematic diagram of tunnel image in fault affected area

在如图3的隧道模型中，实际隧道的排水量由2部分组成，即来自左侧的普通围岩渗流量Q1和右侧来自断层的地下水渗流量Q2。其中，a为隧道与断层的等效距离。左侧的普通围岩渗流可以采用式(3)来计算，而右侧的有限边界渗流量，依据镜像叠加原理，对降深项H2-h2进行叠加。如下式所示。

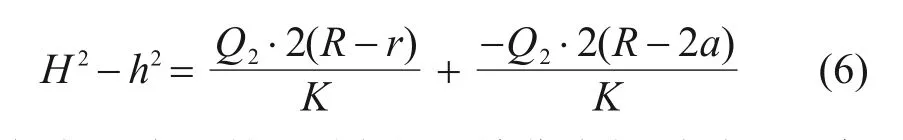
在式(6)中，第2项表征了镜像虚拟隧道对现实隧道处水位下降的贡献。从该项可以发现，当虚拟隧道与现实中的隧道距离2a大于半无限含水层的渗流影响半径R时，虚拟隧道对现实隧道处水位下降的影响几乎为0，所以可以理解为当隧道与断层的等效距离a大于R/2 时，断层作为地下水补给边界的影响可以忽略，地下水仍然可以视为在半无限空间中流动。所以，从地下水渗流补给边界的角度考虑，当隧道与断层的等效距离a小于R/2，需要考虑断层对隧道附近渗流场的影响。

3 单洞隧道在不同断层分区的涌水量预测

隧道在距离断层由远及近，依次会经历普通围岩区Ⅲ，断层影响区Ⅱ，断层破碎区Ⅰ，在不同区域，涌水量计算公式也会不同。

其中，在普通围岩区Ⅲ的隧道单位长度涌水量预测公式为式(4)，在断层影响区Ⅱ，联立式(3)和式(6)，可以得到该区的单位长度涌水量计算公式，如下所示。

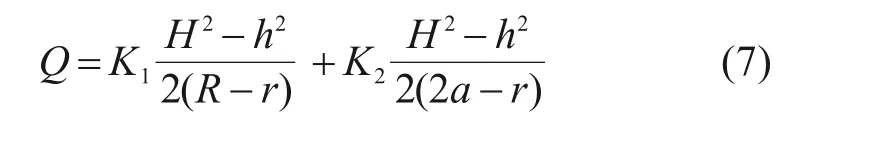
其中，K1为普通围岩区的渗透系数，在均值岩体中可视为常数；K2为断层影响区的渗透系数，该系数需要利用式(5)进行非达西修正，修正过程参考文献[15]，可取ρgk/μ为K2的初试值，计算断层影响范围内的水力梯度J，再代入式(5)，得到新的K2，然后进行第2 轮的计算，直至所计算的水头值趋于稳定。

在断层破碎区Ⅰ，根据文献[12]的研究，当隧道揭露富水断层时，通常为掌子面发生突涌水，涌水量计算公式可以用下式表示。

其中：H为地下水位到隧道内水位的距离，m；F为综合函数，与隧道半径r，m，揭露断层导致突涌水起算的时间t，以及综合变量P有关，该变量与工程地质条件有关，包括渗透系数，储水率，断层宽度以及隧道掌子面到断层边界的距离有关。

综合函数F表达式如下所示。

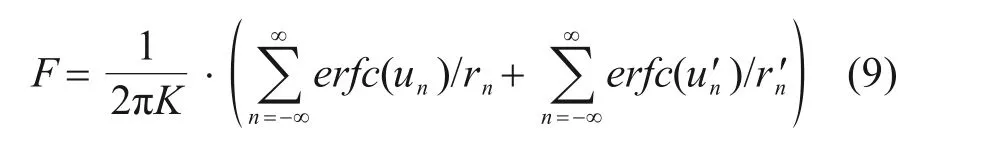
其中：un=rn/(4λΔtij)1/2，rn=2nB，当n=0，rn=r；u′n=r′n/(4λΔtij)1/2，r′n=((2nBcosθ+2H)2+(2nBsinθ)2)1/2，θ为断层的倾角；B为断层宽度；λ=K/Ss，K为断层的渗透系数，Ss为储水系数。

erfc(u)为高斯误差函数，其表达式如下所示。

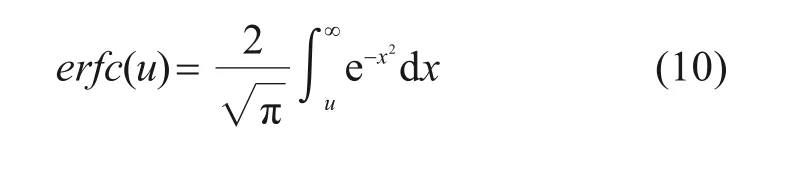
4 双洞隧道在不同断层分区的涌水量预测

基于上述分析，当双洞隧道其中之一位于断层破碎区Ⅰ时，揭露断层中心区Ⅰ的隧道突涌水量可以根据式(8)计算，则另一平行隧道则可视为单洞隧道用按式(7)进行涌水量预测。所以，此处重点讨论双洞隧道在Ⅱ区或Ⅲ区的水量计算。

4.1 两洞皆位于Ⅲ区

计算模型如图4所示。

在如图4的模型中，左右洞外侧地下水流量为Q1，隧道内水位高度为h1；内侧流量为Q2，隧道内水位高度为h2；隧道半径为r，两洞之间轴线距离为L。隧道外侧流量Q1根据式(3)来计算，隧道内侧流量根据叠加原理，计算如下所示。

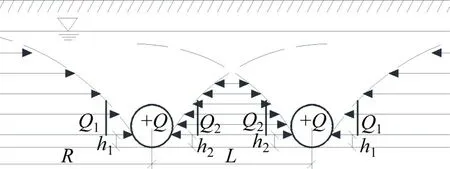
图4 双洞隧道在Ⅲ区模型示意图Fig.4 Schematic diagram of double tunnel model in Zone ⅠⅠⅠ

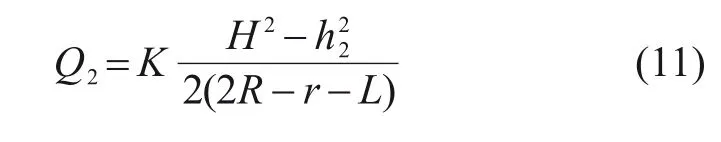
则双洞隧道在Ⅲ区内，单个隧道的单位长度涌水量为Q=Q1+Q2。

4.2 仅一洞位于Ⅱ区

计算模型如图5所示。

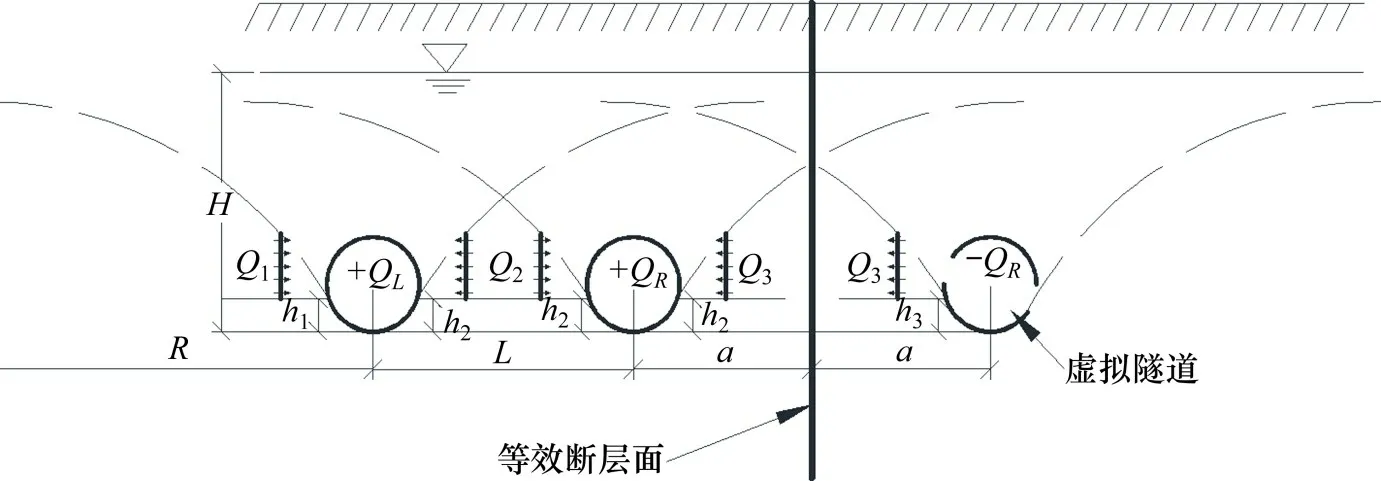
图5 仅右洞隧道位于Ⅱ区内模型示意图Fig.5 Model diagram of only right tunnel in zone Ⅱ

在如图5 的模型中，各参数含义如前面所述。则左洞外侧流量Q1根据式(3)来计算，左洞内侧和右洞内侧流量Q2根据式(11)来计算，右洞外侧流量Q3根据叠加原理，表达式如下。其中：式(12)中的K2为经过非达西修正的渗透系数。所以在此种情况下，左洞单位长度涌水量为QL=Q1+Q2，右洞单位长度涌水量为QR=Q2+Q3。

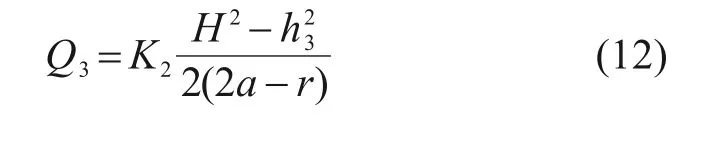
4.3 两洞皆位于Ⅱ区且均在断层一侧

计算模型如图6所示。

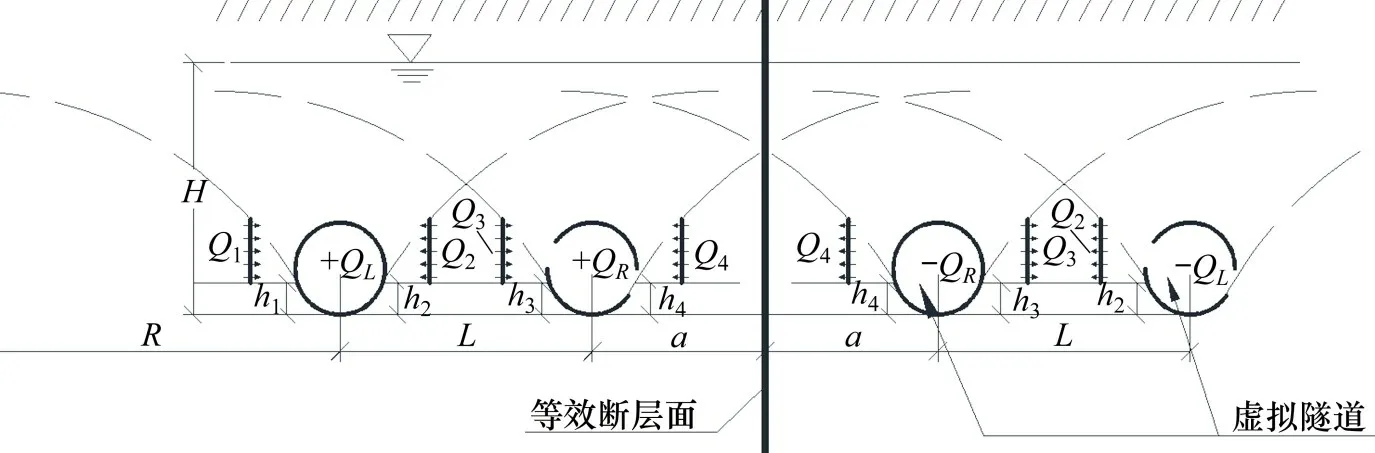
图6 两洞在断层影响范围内处于断层一侧模型图Fig.6 Model diagram of two tunnels on one side of the fault within the influence range of the fault

在如图6 的模型中，各参数含义如前面所述。左洞外侧流量Q1同样根据式(3)来计算，Q2，Q3和Q4根据叠加原理，需要联立方程组来求解，如下所示。

利用式(13)，可求得左洞内侧流量Q2，和右洞内外侧流量Q3、Q4。所以左洞单位长度涌水量为QL=Q1+Q2,右洞单位长度涌水量为QR=Q3+Q4。

4.4 两洞皆位于Ⅱ区且分布在断层两侧

计算模型如图7所示。

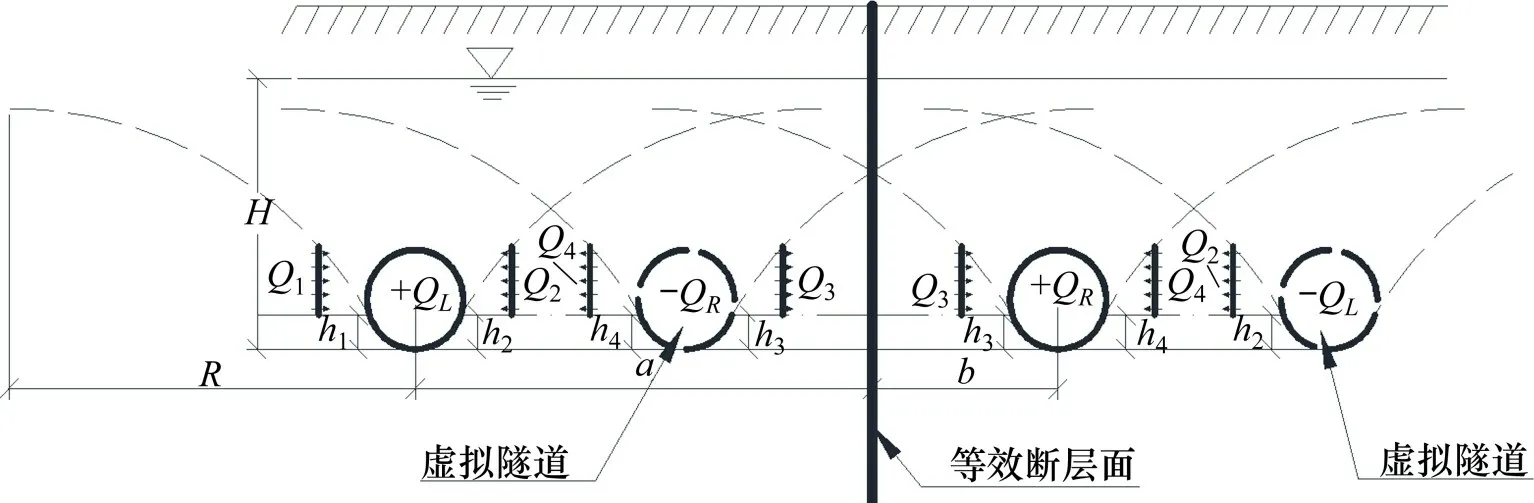
图7 两洞在断层影响范围内且分别位于断层两侧模型图Fig.7 Model diagram of two tunnels within the influence range of the fault and located on both sides of the fault respectively

在图7 的模型中，同4.3 节，左洞外侧流量Q1可用式(3)来计算，Q2，Q3，Q4则需要联立方程组来求解。如下所示。

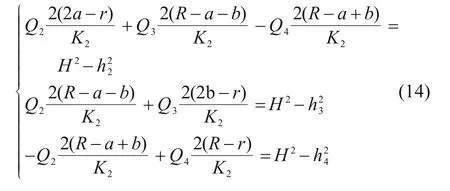
同理，根据式(14)可得到Q2，Q3，Q4的值，从而得到左洞单位长度涌水量QL=Q1+Q2和右洞单位长度涌水量QR=Q3+Q4。

5 案例对比

本文以实际某双洞隧道为依托，选取隧道入口段K89+392 到F3-1 断层带附近K89+693 的段落为分析对象，利用前述方法进行涌水量预测，并结合现场量测验证预测方法的合理性。该区段含水层岩性为中晚侏罗系安山玢岩，以全～强风化土为主，网状裂隙发育，透水性中等。根据相关勘察资料和水文资料，该区段内地形起伏较大，其中普通围岩区Ⅲ海拔较低，地下水平均水位高程为35 m，隧道内的水位取为0.6 m，依据现场渗透试验测试结果，其渗透系数K取为0.894 m/d；而在F3-1 断层影响范围内，由于地处高海拔的山头，地下水平均水位高程为96 m，此断层宽度为5 m，与隧道轴向夹角为75°，根据断层影响区内岩石裂隙大小测定其渗透率k为1×10-8m2，参考文献[15]，该隙宽情况下相应储水系数SS取为0.000 032 m-1，与左线隧道轴线相交于K89+676，与右线隧道相交于K89+690。隧道左右洞横向间距取为50 m，隧道半径为5.9 m，隧道内水位高程取0.6 m。其中，右洞为先行洞，本文重点考虑地下水稳定渗流条件下的隧道出水情况，因此选择施工期左右洞隧道均穿越断层后水流稳定时的水量进行计算对比。

根据式(1)可得到渗流影响半径R为671.9 m，再依据掌子面与断层的等效距离a与R的关系，由此对分析区段进行分区。分区结果如图8所示。

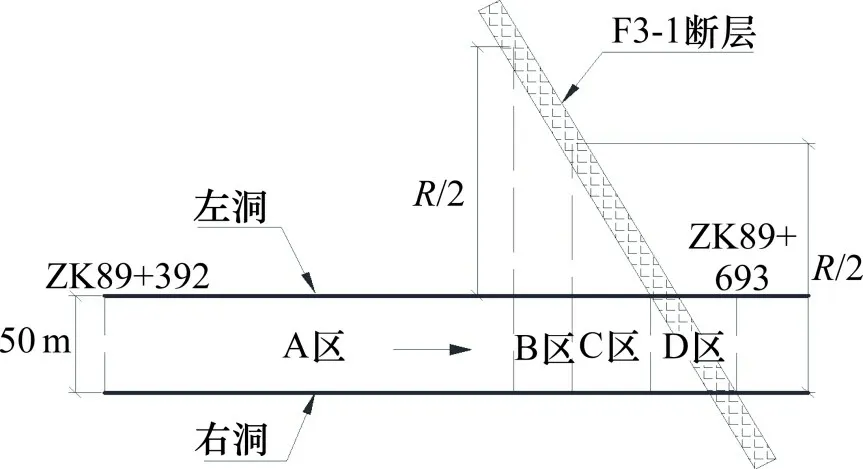
图8 隧道分区示意图Fig.8 Schematic diagram of tunnel zoning

在图8 中，各分区情况为，A 区：左右洞皆位于普通围岩区Ⅲ；B区：左洞位于Ⅱ区，右洞仍位于Ⅲ区；C 区：左右洞皆位于Ⅱ区且均在断层一侧；D 区：由2 部分组成，一部分是左右洞揭露断层，处于Ⅰ区的范围，另一部分为左右洞皆位于Ⅱ区且分布在断层两侧。经过计算，各分区的长度分别为175，14，92和20 m。

将上述各参数代入式(3)、(8)、(11)、(12)、(13)、(14)，可以得到左右洞各分区的涌水量大小，如表1所示。

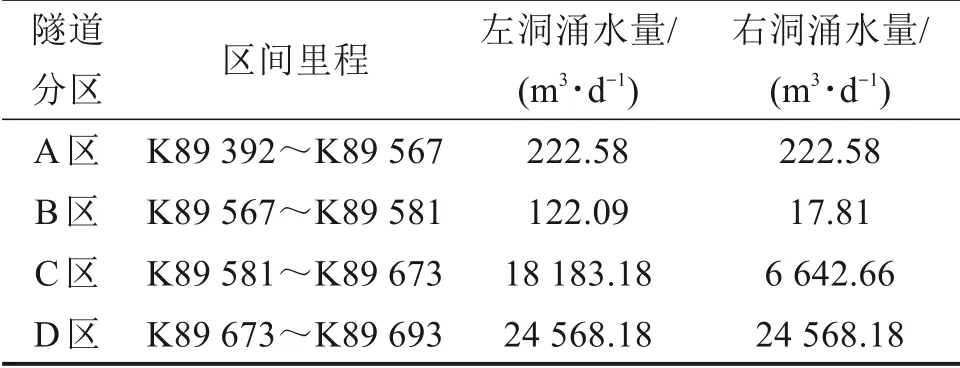
表1 隧道不同分区涌水量大小预测Table 1 Prediction of water inflow in different zones of tunnel

以D 区终点K89+693 为原点，统计在上述分析区内，随着监测点位逐渐远离原点处截面，隧道内涌水量累计值变化。经过现场量测，得到左右洞水量累积变化对比情况，如图9所示。

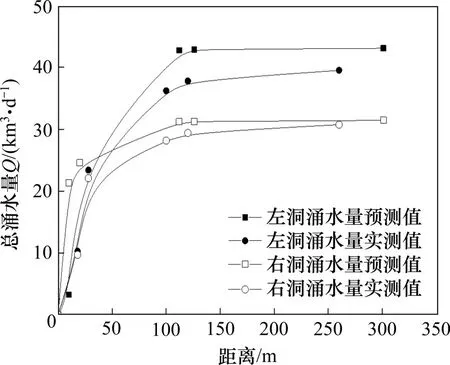
图9 左右洞隧道水量累积变化曲线Fig.9 Water accumulation curves of left and right tunnel

从图9可以看出，在不同断层分区，水量有较为明显的变化，其中，隧道揭露断层的断层破碎区涌水量最大，在断层影响区随着距离断层越来越远，水量逐渐变缓，最终在普通围岩区涌水累积量以相对较小的斜率保持线性增加，并趋于稳定。2 图所示的涌水量预测值与实际值大小较为接近，但比实际值要大，主要是由于理论分析中采用的平均地下水位在实际工况中某些区间并未达到设定的高度，且隧道做了相关防水措施。但本文所述的双洞隧道涌水量计算方法依然可作为隧道开挖后涌水量的预测手段，可以为工程设计、施工安全提供指导。