基于拓扑优化理论的悬索桥双吊杆索夹优化设计
2022-08-29刘卧唐冕宋旭明胡省阳
刘卧,唐冕,宋旭明,胡省阳
(1. 中南大学 土木工程学院,湖南 长沙 410075;2.中国铁路设计集团有限公司,天津 300142)
自锚式悬索桥的桥面荷载通过吊索和索夹传递给主缆,因此主缆和吊索的连接是关键部位[1-2]。索夹[3]是工程实践中主缆和吊索普遍采用的连接构件,考虑自锚式悬索桥施工周期较长、施工工艺复杂等因素,进一步增大了主缆与索夹锚固系统相互作用的复杂性,该部位的安全可靠性直接影响全桥结构的可靠度,是桥梁设计的关键部位之一。《公路悬索桥设计规范(JTG/T D65-05—2015)》[4]中提出索夹的设计应根据吊索力和吊索处主缆的倾角进行分类设计,对主要受力部位制定了相关的构造要求及力学性能要求,而关于索夹空间具体形式的设计,如弧形板的尺寸和耳板的形式等,规范中并未给出明确规定及参考意见。目前,索夹设计仍主要取决于相应的力学标准及设计者的经验,该方法存在明显的局限性,无法得到最优的索夹结构。基于以上原因,进行自锚式悬索桥索夹的优化设计是十分有必要的。结构优化设计是指使工程结构在满足支撑和荷载条件下按预定目标设计得到的优化方案,其目标是以最少的材料或最低的造价实现结构的最优性能[5]。结构优化分为尺寸、形状和拓扑优化3 个层次[6],其中,拓扑优化比尺寸和形状优化节省材料更显著,被认为是一个更具有挑战性的领域,可以广泛应用于土木、机械、航空、航天器及船舶制造等领域[7-9]。目前,比较成熟的拓扑优化方法有均匀化方法、渐进结构优化法和变密度方法等[10-11]。本文以长沙市三汊矶湘江大桥为工程背景,以双吊杆索夹为研究对象,基于变密度法连续体拓扑优化设计理论,综合考虑索夹的空间状态对索夹结构受力的影响,对自锚式悬索桥的双吊杆索夹开展优化设计,为同类索夹设计提供一种可行方案。
1 工程背景及拓扑优化理论
1.1 工程背景
长沙市三汊矶湘江大桥是一座大跨度自锚式悬索桥,跨径布置为(70+132+328+132+70)m。
索夹采用左右对合、销接带耳板的形式,2 片索夹用高强螺栓夹紧。图1 是倾角为0°的索夹结构,其余索夹结构根据倾角进行相应的局部调整,与倾角为0°时的形状大致相同。索夹采用ZG270-500铸钢铸造,索夹相关参数如表1所示。
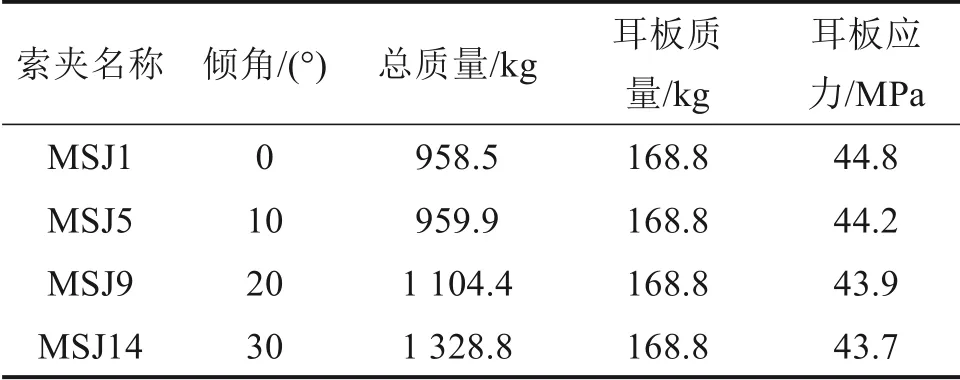
表1 工程背景中索夹参数Table 1 Cable clamp parameters in the engineering background
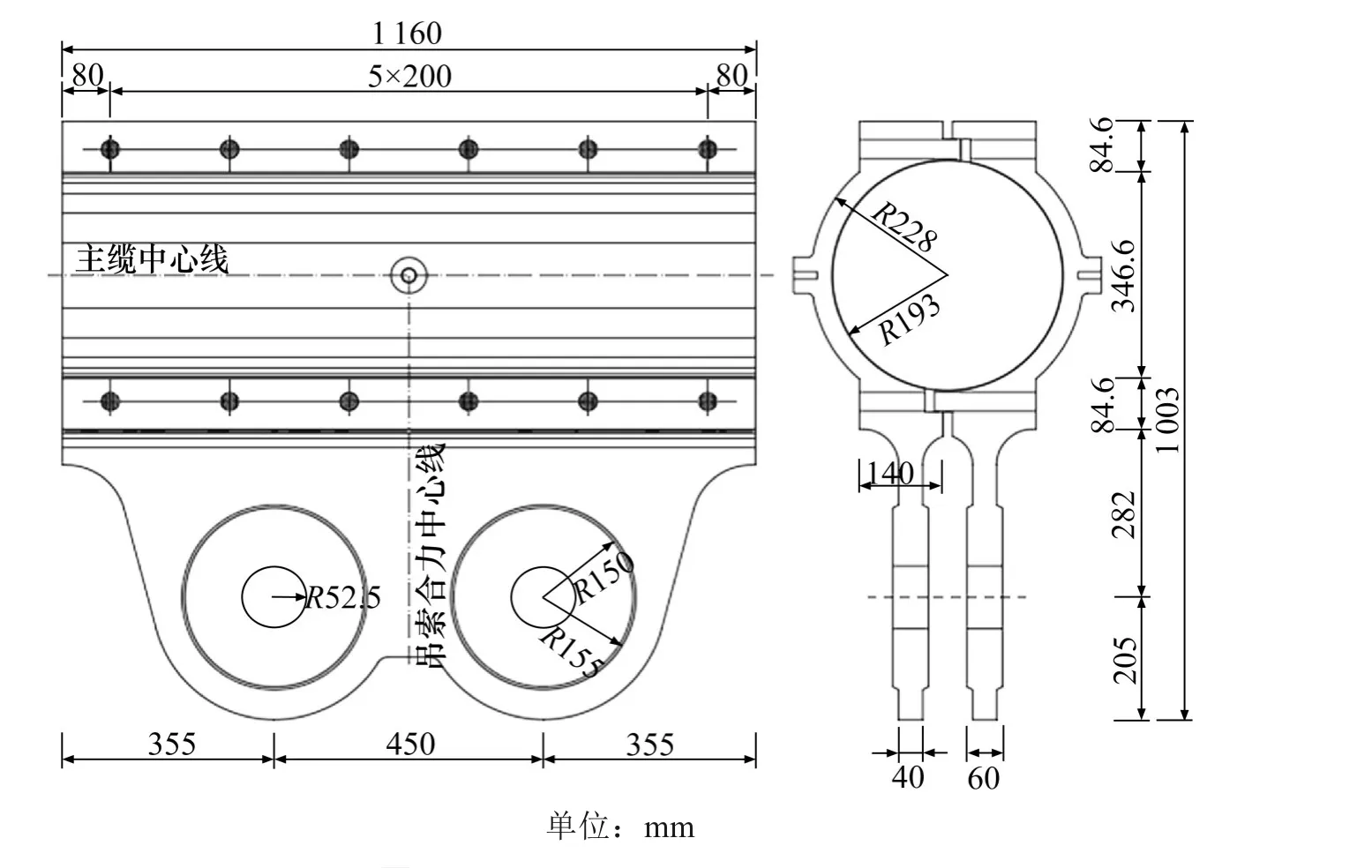
图1 工程背景中索夹结构(θ=0°)Fig.1 Cable clamp structure in engineering background
1.2 拓扑优化理论
本文采用变密度法连续体拓扑优化理论,其基本思想是引入单元相对密度作为优化设计变量,在离散型优化问题中,单元优化设计变量取值为0或1[12-13],由于单元相对密度的引入,单元优化设计变量的取值在区间[0,1]上连续,从而将离散型优化问题转换成连续型优化问题。
1.2.1 SⅠMP材料插值模型
在变密度法连续体拓扑优化过程中,目前较普遍采用SⅠMP 插值模型法[14-16]来压缩中间密度材料。
以结构的最小柔度问题为例,在SⅠMP 材料插值模型方法的基础上,连续体拓扑优化问题数学模型如式(1)所示:
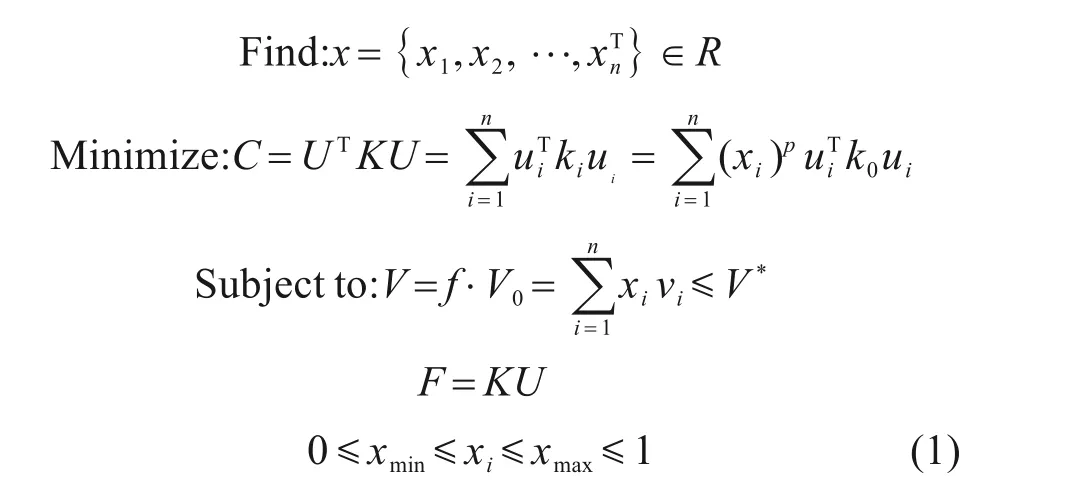
式(1)中各字母的具体含义见文献[17]。
1.2.2 优化准则
在变密度法连续体拓扑优化时,目前较普遍采用优化准则法[17]来对拓扑优化数值模型进行求解分析,例如OC算法和COC算法等。
基于优化准则法的变密度法连续体拓扑优化数学模型可表示如下:
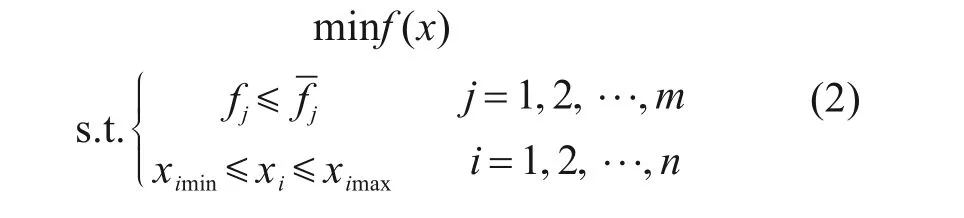
将优化数学模型中的目标函数和约束条件构造成拉格朗日函数:
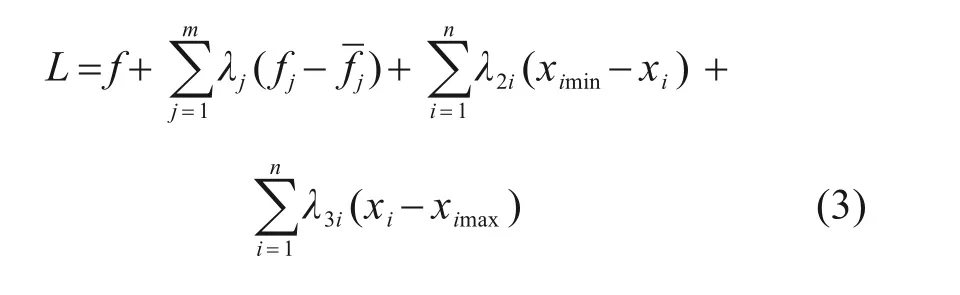
式(2)~(3)中各字母的具体含义见文献[17]。
2 索夹基本结构及其性能评估
2.1 索夹基本结构
以Atair Optistruct 软件作为有限元分析平台,取索夹耳板及过渡部位作为主要研究对象,分析双吊杆索夹优化前基本结构的力学性能。
分别建立不同倾角下索夹有限元模型,倾角分别为0°,10°,20°及30°。索夹材料设置为铸钢,其弹性模量为E=2.05×105MPa,泊松比μ=0.3,密度ρ=7.85×103kg/m3,采用六面体网格划分,索夹基本结构如图2所示。索夹在空间上受到主缆的约束作用,其空间状态较稳定,本文将索夹基本结构弧形板整体视为固定约束,荷载条件取平均总吊索力1 050 kN,根据索夹倾角不同,荷载条件进行相应的调整,以竖向与横向的合力方式施加,见表2。
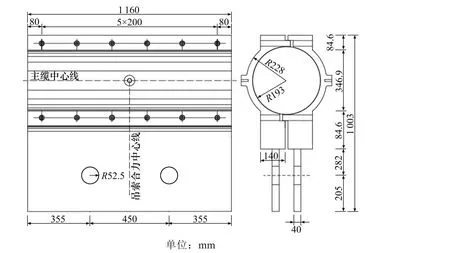
图2 索夹基本结构(θ=0°)Fig.2 Basic structure of cable clamp(θ=0°)
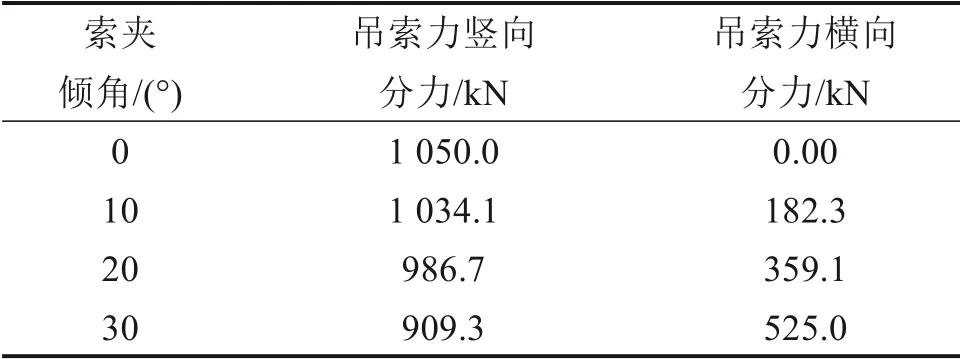
表2 吊索力施加方式Table 2 Application mode of sling force
2.2 变形分析
图3是吊索力为1 050 kN,索夹倾角为0°时双吊杆索夹基本结构的耳板变形云图;表3为不同倾角索夹基本结构的最大变形量和等值线(相对0°时)倾斜的情况。
由图3 和表3 可知,当索夹倾角为0°时,耳板变形呈现沿耳板中心线对称式分布,最大变形量为0.027 mm,出现在耳板开孔的下部。随着倾角的变化,索夹耳板内部传力途径发生改变,耳板的变形会发生适应于倾角变化的调整。例如,当索夹倾角为10°时,其变形等值线相对倾角为0°时变形等值线发生了角度约11.3°的倾斜;其最大变形量为0.028 mm,出现在耳板开孔的下部,相对于倾角为0°时最大变形量0.027 mm 变化不大,对结构安全性能无太大影响。对于其他倾角的索夹结构亦可得出类似结论。
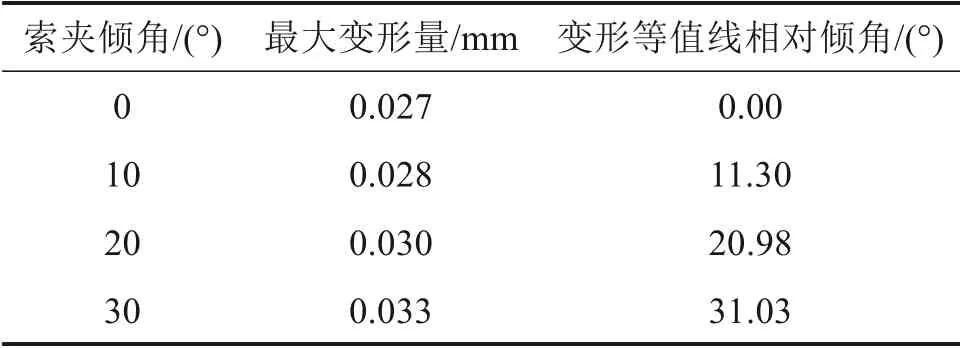
表3 索夹基本结构变形情况Table 3 Deformation of the basic structure of the cable clamp
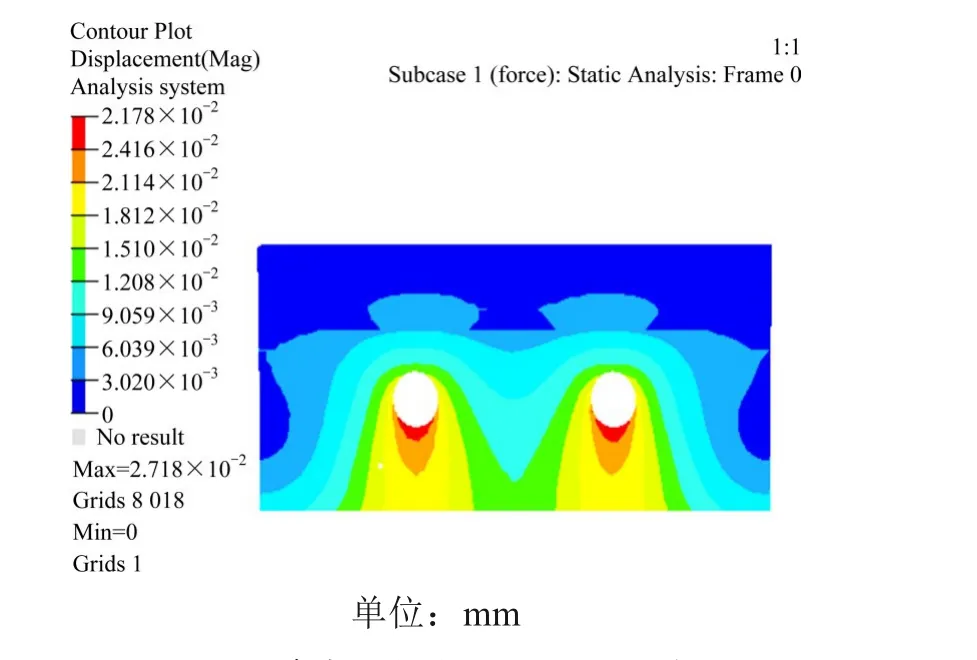
图3 基本结构变形云图(θ=0°)Fig.3 Deformation cloud diagram of basic structure
2.3 应力分析
图4是吊索力为1 050 kN,索夹倾角为0°时双吊杆索夹基本结构的耳板Von Mises 应力云图;表4 为不同倾角索夹基本结构的最大应力值和应力等值线(相对0°时)倾斜的情况。
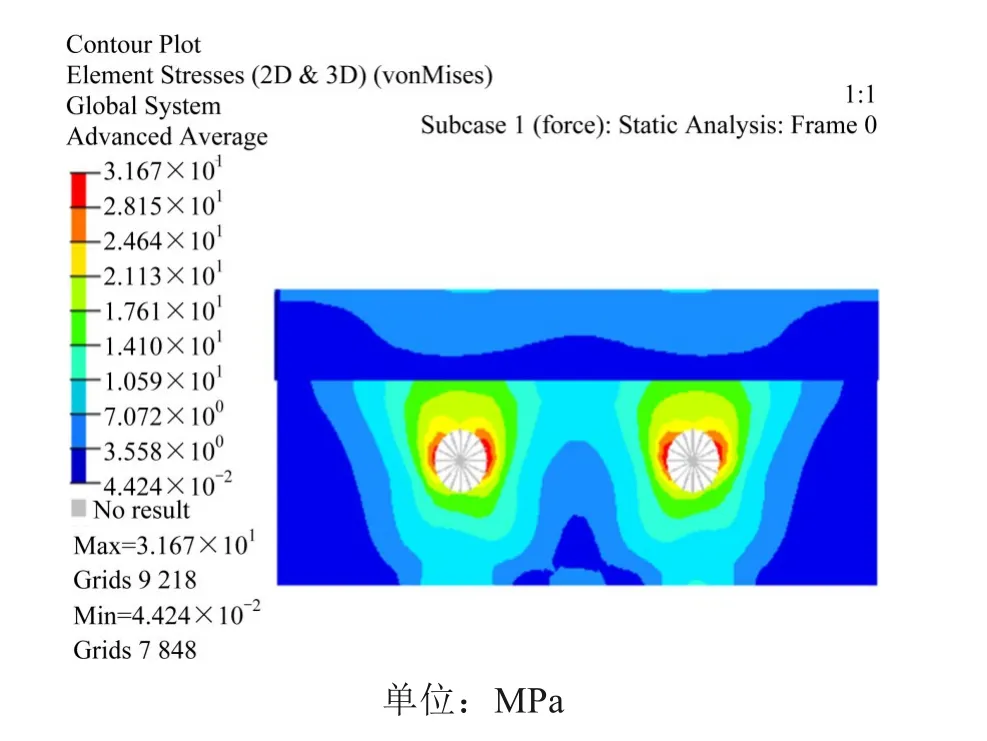
图4 基本结构应力云图(θ=0°)Fig.4 Basic structural stress nephogram
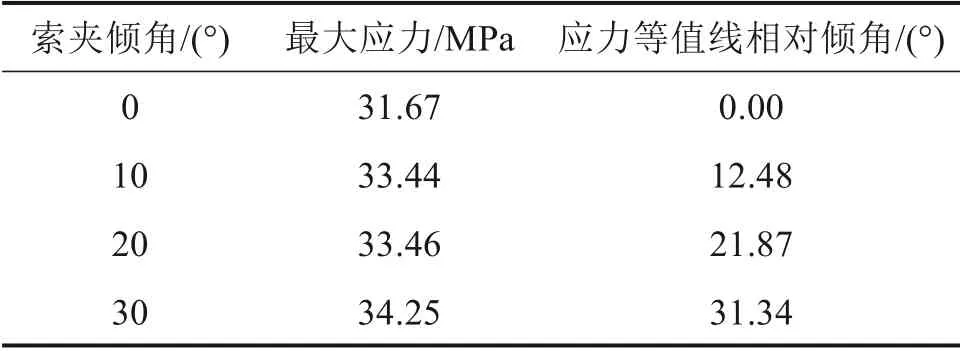
表4 索夹基本结构应力情况Table 4 Basic structural stress of cable clip
由图4 和表4 可知,当索夹倾角为0°时,耳板Von Mises 应力呈现沿耳板中心线对称式分布,最大Von Mises 应力为31.67 MPa,分布在吊孔周围。随着倾角的变化,索夹耳板内部传力途径发生改变,耳板的应力会发生适应于倾角变化的调整。例如,当索夹倾角为10°时,其应力等值线相对索夹倾角为0°时应力等值线发生了角度约12.48°的倾斜;其最大应力为33.44 MPa,分布在吊孔周围,相对于倾角0°时最大应力31.67 MPa 变化不大,满足结构安全要求;其他倾角的索夹结构亦可得出类似结论。
3 拓扑优化模型及结果
3.1 拓扑优化模型
双吊杆索夹拓扑优化设计的目的是在满足其基本受力条件下得到轻质、高强、低柔顺性结构,即要求利用最少的原材料最优地分布于索夹耳板的设计区域。当采用变密度法拓扑优化理论时,考虑到对于金属这类材料,可利用体积间接反映优化后的结构质量。因此,在优化过程中将索夹耳板设计区域的体积作为目标函数,将其在拓扑优化设计过程中的更新迭代结果作为判断结构优化好坏的依据。具体设计参数如下所示。
响应:体积响应、位移响应;
设计变量:单元相对密度;
约束条件:最小柔顺性约束;
设计目标:体积最小(即质量最小)。
选用SolidWorks 创建索夹三维实体模型,并导入有限元分析平台Atair Optistruct,将索夹耳板及过渡部位设置为拓扑优化设计区域,索夹弧形板设置为非设计区域,索夹材料、弹性模量、泊松比、密度、约束条件及荷载水平等相关参数与索夹基本结构静力分析模型保持一致,采用六面体网格划分,分别建立倾角为0°,10°,20°及30°的索夹拓扑优化有限元模型。
3.2 拓扑优化结果分析
在HyperView中,拓扑优化后结构的设计变量即单元相对密度显示在0~1 范围内,通过调节密度当前值current-value,使密度接近0 的浅色单元都不显示,尽量让密度接近1的深色单元显示。结果表明,双吊杆索夹优化良好,目标函数收敛较快,对于索夹耳板的拓扑优化结果,在HyperView中选取密度current-value为0.5。
图5是吊索力为1 050 kN,倾角为0°时的索夹耳板拓扑优化模型;图6 是索夹设计控制参数图;表5为不同倾角的索夹结构经拓扑优化后耳板两侧边倾角α和β的变化情况。

表5 拓扑优化后索夹耳板两侧边倾角Table 5 Ⅰnclination angles of both sides of the cable clamp ear plate after topology optimization
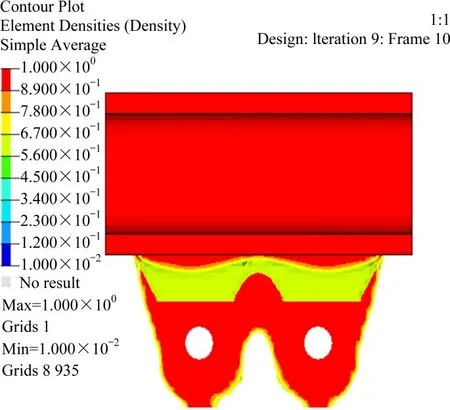
图5 拓扑优化后模型图(θ=0°)Fig.5 Model diagram after topology optimization
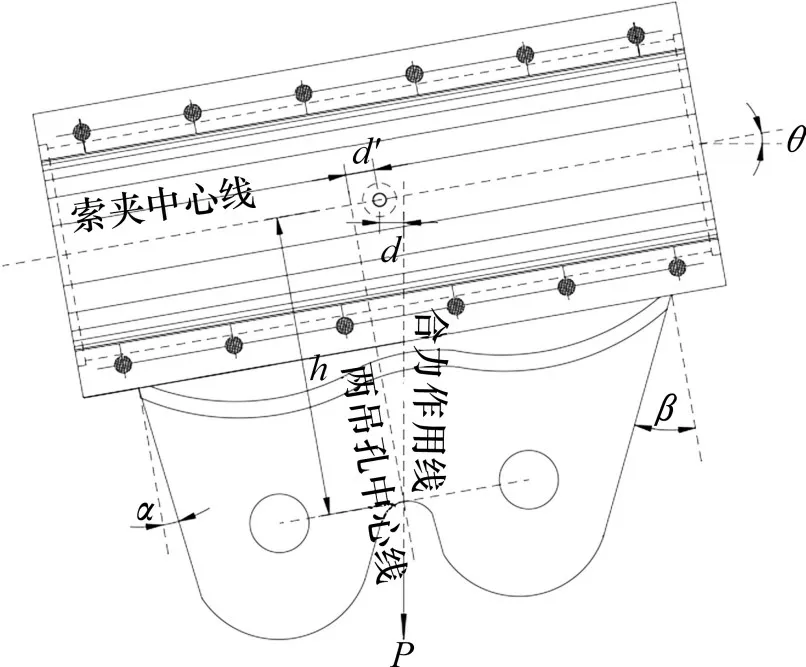
图6 索夹设计控制参数Fig.6 Cable clamp design control parameters
当索夹倾角为0°时,索夹耳板呈对称式分布,弧形板与索夹耳板之间产生过渡部位,即图5中浅色部分,该过渡段的单元密度在0.5~0.67 之间。将拓扑优化后索夹结构与索夹基本结构应力云图进行对比,显示二者具有一定相似性。因此,在进行索夹概念设计时,可依据吊索力计算索夹结构的应力状态,参考其应力等值线削减多余材料。
从图5 和表5 可知,索夹倾角10°时耳板两侧边倾角α和β分别为7°和26°,相对于索夹倾角0°时两侧边倾角变化的绝对值分别为10°和9°,与索夹倾角增幅10°大致相等,即倾角10°时索夹结构耳板侧边倾角变化的幅度与索夹倾角θ增加的幅度近似相等;其他倾角的索夹结构亦可得出类似结论。因此,考虑倾角影响的双吊杆索夹进行初步设计时,可依据无倾角双吊杆索夹的结构形式,对索夹耳板侧边线做出相应的角度调整。
文献[18]研究表明索夹脱空角范围随吊索力增大而增加且受吊索力合力点的影响;文献[4]建议吊索合力通过索夹中心,这是索夹设计的基本要求。在索夹抗滑能力满足规范要求时,如果不偏移吊孔位置,通过加长索夹一端长度使索夹中心偏移至吊索合力方向上,该设计方法易造成索夹材料浪费,且由于索夹尺寸较大,增大了吊装施工难度。因此,在双吊杆索夹优化设计时应适当调整耳板吊孔位置,使整体结构受力均匀。
根据几何关系可直接计算得到吊杆合力的偏移距离d,当吊孔距索夹中心距离h一定时,偏移距离d随主缆倾角增大而增大。由于自锚式悬索桥主缆垂跨比较大,主缆倾角较大,若直接以吊杆合力的偏移距离d作为吊孔偏移依据,索夹长度、吊孔位置及结构受力三者很难耦合。
根据索夹拓扑优化模型,随着索夹倾角的变化,索夹耳板结构不再关于2个吊孔中心线对称式分布,此时索夹耳板及过渡部位相对于索夹中心发生了偏移。经测量:索夹倾角为10°时,偏移距离d′约为80 mm;索夹倾角为20°时,偏移距离d′约为140 mm;索夹倾角为30°时,偏移距离d′约为200 mm。
由此可知,以索夹耳板及过渡部位为设计区域的双吊杆索夹进行拓扑优化,在控制2个吊孔中心距离不变时索夹设计区域产生相对于索夹中心的整体偏移,偏移的主要原因是调整索夹吊孔位置使吊索合力尽可能地通过索夹中心。分析表明,拓扑优化模型的偏移距离d′与吊索合力的偏移距离d虽存在一定的差距,但总体相差不大,且二者存在明显的线性函数关系,如图7所示。
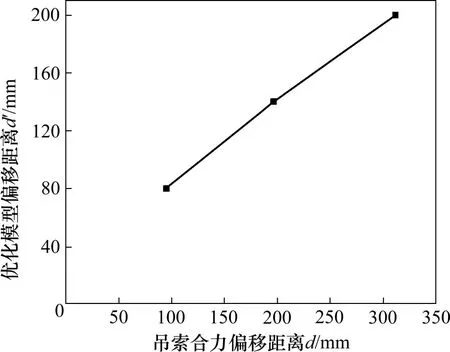
图7 吊孔偏移距离与吊索合力偏移距离关系Fig.7 Relationship between offset distance of lifting hole and resultant offset distance of sling
经线性回归分析,得到优化后索夹形状的简化拟合公式,即d′与h的函数表达式:
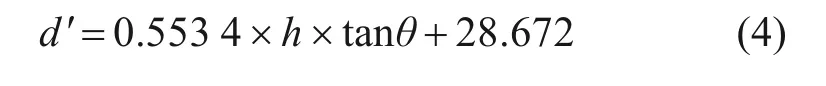
式中:d′为吊孔偏移距离优化值,mm;h为双吊孔连线中心距索夹中心线距离,mm;θ为索夹倾角,(°)。注意,当索夹倾角为0°时,偏移距离为0 mm。
4 新型索夹设计及性能评估
4.1 新型索夹结构设计
通过Ossmooth 工具导出拓扑优化粗糙结构,并利用Solidworks对结构进行修复和删减,捕捉粗糙结构的主要特征,去除多余线条,对可能出现应力集中部位进行平滑过渡,遵循索夹材料分布规律,通过偏移耳板吊孔位置对双吊杆索夹进行二次设计。图8 是倾角为0°时新型索夹结构外侧图,表6 为不同倾角的新型索夹结构的具体参数情况。

表6 新型索夹结构的参数Table 6 Parameter table of the new type of cable clip structure
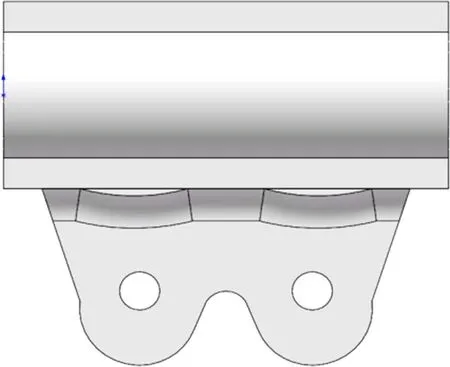
图8 新型索夹结构(θ=0°)Fig.8 New type of cable clip structure(θ=0°)
4.2 新型索夹性能评估
对最终确定的新型索夹结构进行静力分析,其中,最大变形量和最大应力值都出现在索夹倾角为30°时,如图9~10 所示。由结果可知,不同倾角的新型索夹最大变形量约为0.046 mm,发生在吊孔下方,最大Von Mises应力约为50 MPa,小于ZG270-500铸钢索夹材料的抗拉强度设计值,满足结构安全要求。
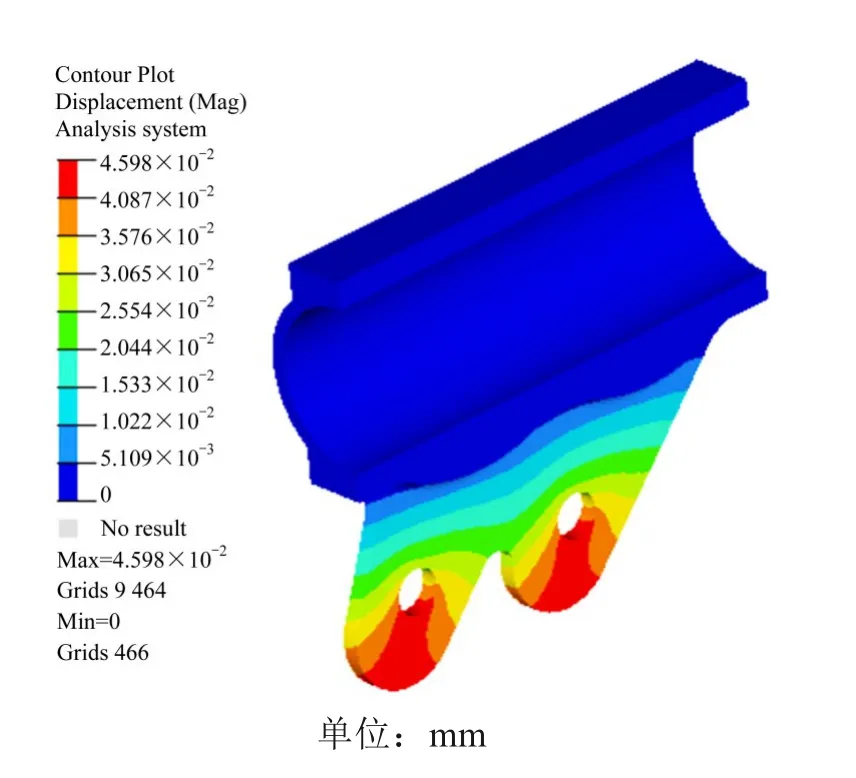
图9 新型索夹变形云图(θ=30°)Fig.9 Deformation nephogram of new cable clip
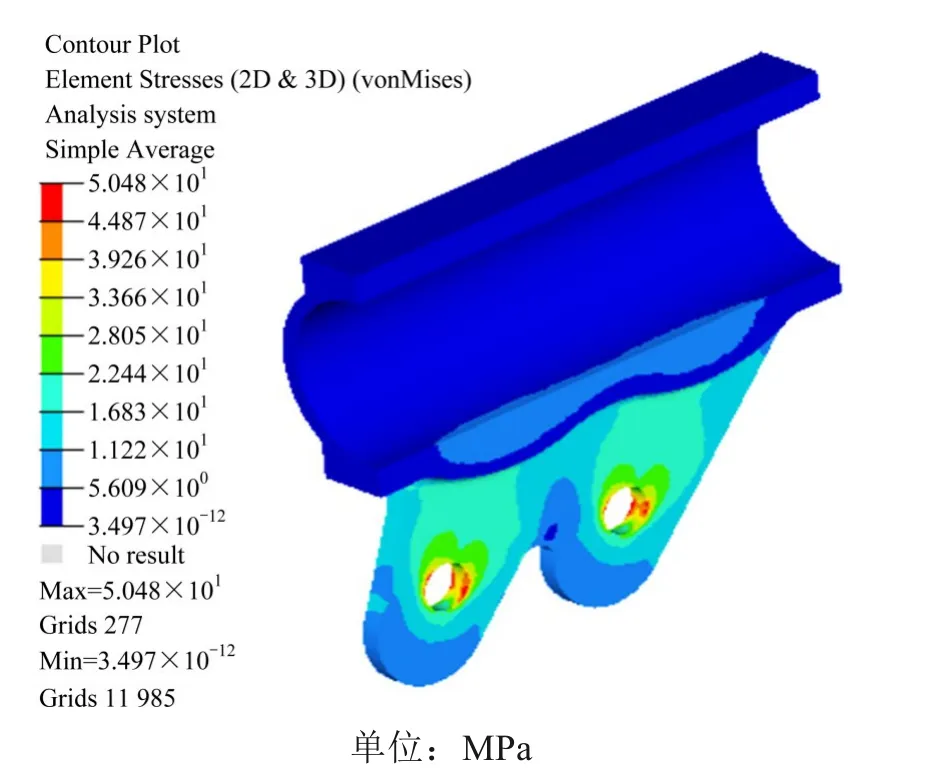
图10 新型索夹应力云图(θ=30°)Fig.10 Stress nephogram of new type cable clip
由表7可知,相较于双吊杆索夹优化前基本结构,不同倾角的新型索夹结构耳板减重约57%;相较于工程背景索夹结构,不同倾角的新型索夹结构耳板减重约20%。由表8 可知,新型索夹结构耳板安全系数约为1.8,原工程背景中索夹结构耳板安全系数约为2.0,新型索夹结构仍具有较大的安全储备。
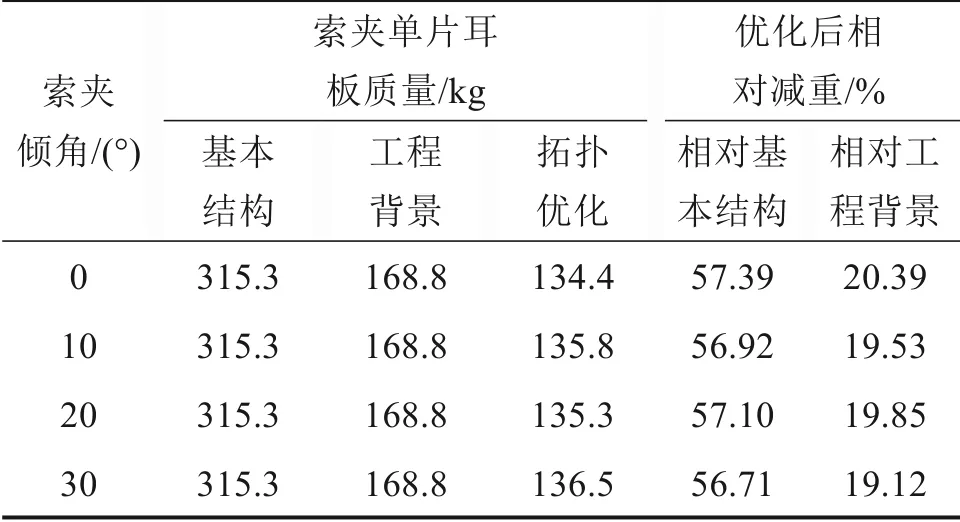
表7 索夹耳板质量对比Table 7 Weight comparison of cable clamp ear plates
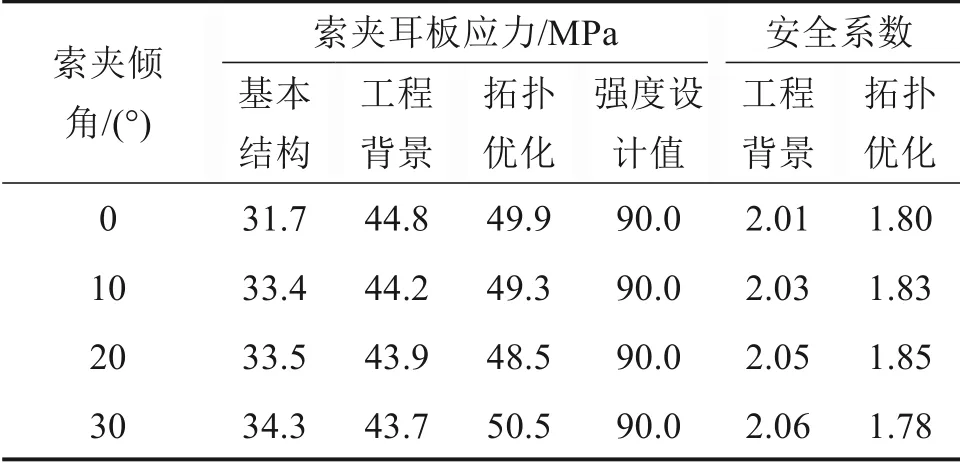
表8 索夹耳板力学性能Table 8 Mechanical properties of cable clamp ear plate
5 结论
1) 当索夹倾角为0°时,索夹耳板呈对称式分布,将拓扑优化后索夹结构与索夹基本结构应力云图进行对比,结果显示二者具有一定相似性,可依据索夹基本结构应力等值线进行索夹概念设计。
2) 以倾角为0°时的优化结果为参照,对比不同倾角索夹的拓扑优化结果中侧边线角度变化幅度,结果显示索夹侧边线角度变化的幅度与倾角θ增加的幅度近似相等,故考虑倾角影响的双吊杆索夹进行初步设计时,可依据无倾角双吊杆索夹的结构形式对索夹耳板侧边线做出相应的角度调整。
3)当倾角为10°,20°及30°时,双吊杆索夹耳板及过渡部位在拓扑优化过程中发生相对于索夹中心的偏移,偏移量分别为80,140 及200 mm,其主要原因是调整索夹吊孔位置使吊索合力尽可能地通过索夹中心;优化后得到索夹形状的简化拟合公式,在满足索夹抗滑及结构受力均匀的前提条件下使材料达到最省。
4) 新型索夹结构耳板相较于基本结构减重约50%~60%,相较于工程背景索夹结构减重约20%,且仍具有较大的应力安全储备。根据拓扑优化方法设计的双吊杆索夹在考虑索夹倾角影响的同时,实现结构轻质、高强和经济的设计目标。
