人行悬索桥吊杆的损伤识别
2022-06-24张彦玲侯屹峰王泽涵
张彦玲, 侯屹峰, 王泽涵, 曹 杨
(1.石家庄铁道大学 道路与铁道工程安全保障省部共建教育部重点实验室,河北 石家庄 050043;2.石家庄铁道大学 土木工程学院,河北 石家庄 050043)
在悬索桥中,主梁及桥面系自重及外荷载均通过吊杆传递给主缆,一旦吊杆发生损伤,会对悬索桥的正常使用甚至安全性能产生较大影响[1],其中最新的报道是在2022年1月18日下午,某千米级跨江轨道悬索桥的一根吊杆发生断裂,导致列车无法正常通过,因此对于吊杆损伤对桥梁的影响分析和损伤识别研究至关重要。车行悬索桥一般跨度较长,桥面较宽,吊杆间距相对较大,且桥面会提供必要的刚度以满足行车舒适性,但对于近年来修建数量逐渐增多的人行悬索桥,由于其柔性更大,刚度更小,吊杆间距相对较小,因此吊杆损伤对桥梁产生的影响需要进行专门的分析。
结构损伤识别的主要方法是使所构造的损伤指标在损伤处发生的变化要比未损伤处明显,因此选择一种合适的损伤指标至关重要。早期 Pandey et al[2]提出基于曲率模态的方法来识别结构是否发生损伤以及损伤的位置,以此为基础,研究人员陆续提出了基于模态柔度差、模态曲率差、模态应变能等指标[3-6]。郑明刚等[7]将曲率模态用于桥梁状态监测,结果表明,曲率模态对结构损伤较为敏感;刘义伦等[8]提出了曲率振型规范化的处理方法,并对曲率零点处的变化量计算作了特殊处理,以避免此处引起的损伤识别干扰;包龙生等[9]利用BP神经网络与传统的曲率模态理论相结合研究桥梁的损伤,李杰等[10]构造广义柔度曲率矩阵对角指标进行桥梁的损伤识别。
上述指标基本都可用于损伤程度及损伤位置的识别,但所针对的对象主要为梁式结构中的主梁梁体本身,而对于悬索桥,吊杆的损伤或断裂相当于主梁边界条件的改变,与主梁本身的损伤在机理上有所不同,且目前尚无专门针对人行悬索桥进行吊杆损伤研究的报道。因此基于模态分析,以某主跨为192 m的人行悬索桥为研究对象,对吊杆的损伤识别方法进行研究。
1 工程背景及有限元模型
以位于福建省某景区的人行悬索桥为例,其跨度为(15+192+30)m,中跨长度L=192 m。主缆矢跨比1/10,矢高19.2 m;抗风缆计算跨度201 m,矢跨比1/12;吊杆间距顺桥向3 m,横桥向2.8 m;桥面计算宽度2.3 m,主塔高度为26.4 m。在桥面3/8跨位置设置2个观景台。主缆采用预制平行钢丝束;加劲梁主梁由横梁和纵梁组焊而成,采用Q345钢材,纵梁内部灌有混凝土进行压重,桁梁标准节长度为3 m;吊杆采用强度为1 670 MPa,由13根5 mm粗的高强镀锌钢丝成品索;主塔采用C30混凝土;玻璃桥面宽度2.3 m,吊杆处横梁宽度3.0 m。桥梁总体布置如图1所示。

图1 人行悬索桥总体布置图(单位:m)
该桥在建设完成但抗风缆尚未张拉时进行了自振特性的现场实测。根据实测数据,在振动测试系统中对中跨桥面板进行模态分析,得到实测频率和振型。同时采用Midas软件建立有限元模型,通过建模助手对主缆进行找形。主缆采用wire1860单元,吊杆采用只受拉桁架单元,主梁采用梁单元。边界条件为:主缆和主梁固结,释放顺桥向;主梁和主塔通过固定铰支座和活动铰支座连接。由于在现场实测时抗风缆尚未张拉,为了与测试结果进行对比,有限元模型中也未建立抗风缆。Midas模型如图2所示,在以下的分析中,考虑一侧主缆下方的吊杆发生损伤,称其为“损伤侧”,见图2(a);模型中两塔之间每侧主缆下方共63根吊杆,图2(b)中给出了损伤侧半跨内的吊杆编号,标出序号的吊杆为后续损伤分析的研究对象。

图2 有限元模型
采用有限元模型进行模态分析,与实测结果进行对比,前6阶竖向振动结果见表1。表1中频率误差e=(有限元频率-实测频率)/实测频率。
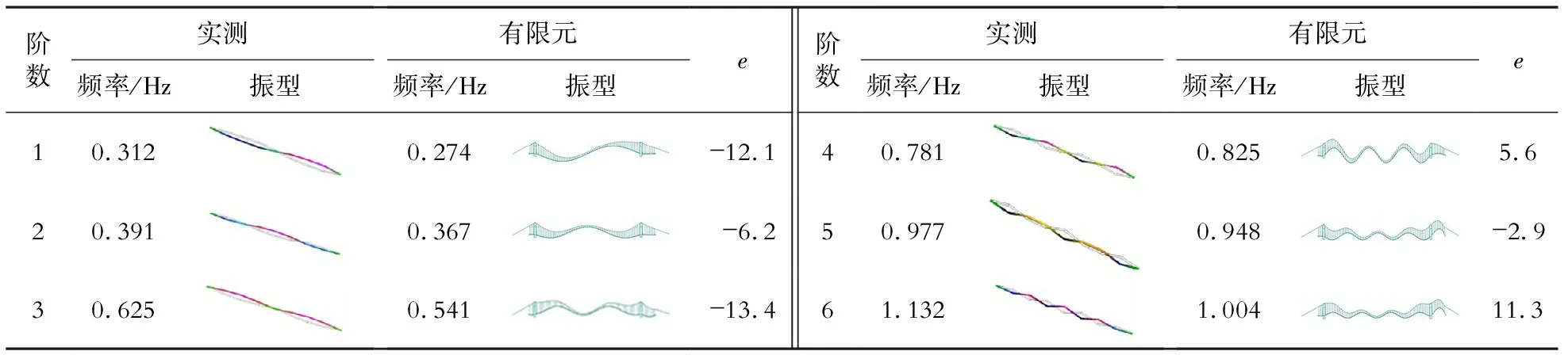
表1 自振频率实测值和有限元值的比较
由表1可知,实测频率与有限元频率误差很小,可以根据该有限元模型进行吊杆损伤后的分析。
2 吊杆损伤和断裂对人行悬索桥静、动力性能的影响
通过鲁棒性分析,发现1、11、16、22、31号吊杆及其沿纵向对称位置的吊杆对该桥静、动力特性影响较大,以下选取上述吊杆(以下称为“关键吊杆”)作为研究对象,分析吊杆损伤或断裂对人行悬索桥的静、动力性能的影响。
2.1 吊杆损伤和断裂对静力性能的影响
2.1.1 对吊杆拉力和应力的影响
在有限元模型中采用减小截面面积的方式模拟关键吊杆的损伤,损伤度分别取10%、50%、75%和100%(断裂)。某吊杆损伤后各吊杆的拉力和应力变化如图3所示,图3中吊杆拉(应)力增幅=(吊杆损伤后拉(应)力-吊杆完好状态下拉(应)力)/吊杆完好状态下拉(应)力。
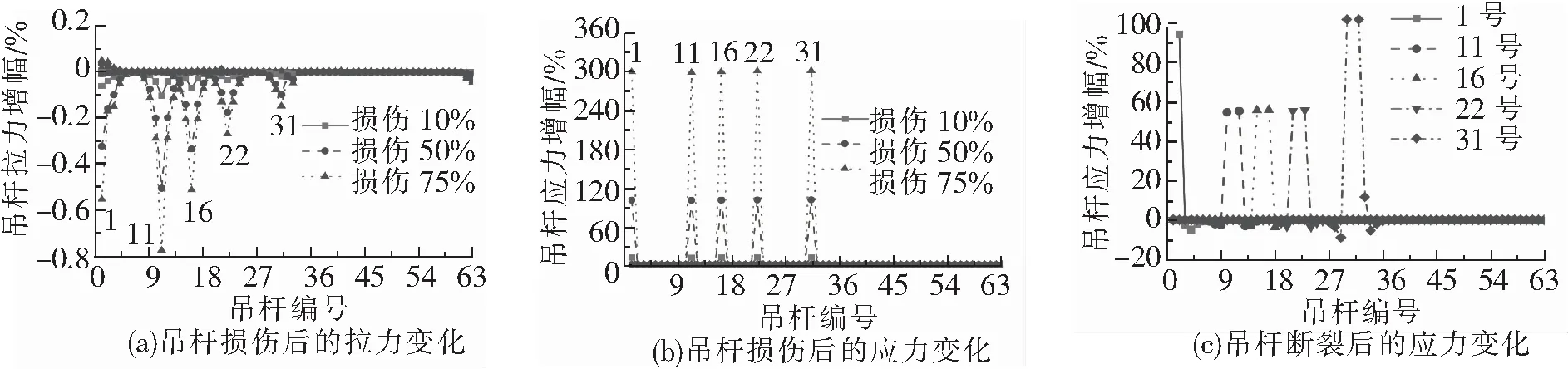
图3 吊杆损伤和断裂后吊杆拉力和应力的变化
由图3可知:① 随着吊杆损伤程度的增加,损伤吊杆的拉力减小,损伤程度越大,减小程度越大,但即使吊杆已发生75%的损伤,吊杆拉力的减小量也不到1%,可见吊杆损伤对其索力的影响较小;② 随着吊杆损伤程度增加,损伤吊杆的应力增大,但一根吊杆的损伤所产生的影响范围很小,仅局限在该损伤吊杆本身,只要吊杆未发生断裂,即使损伤程度达到75%,其相邻吊杆的应力也基本不发生变化;③ 1号边吊杆断裂后,相邻的2号吊杆应力增加了94.3%,3~8号吊杆应力略有减小,其余吊杆应力变化很小,11号吊杆断裂后,在左右相邻的10号和12号吊杆应力分别增加了54.7%和55.3%,6~9号和13~16号吊杆的应力均略有减小,其余吊杆应力增幅均小于0.1%;跨中的31号吊杆断裂后,相邻的30号和32号吊杆应力增幅明显,23~29号和34~39号吊杆的应力均略有减小,其余远离31号吊杆的应力增幅接近于0。
由以上分析可知,吊杆损伤对其拉力影响很小,但损伤吊杆的应力增大。断裂对其相邻吊杆的应力影响最大,相邻吊杆外侧2~3根吊杆范围吊杆应力则略有减小,超过此范围则不再产生影响。
2.1.2 对主梁位移、弯矩和主缆轴力的影响
各关键吊杆断裂对恒载作用下损伤侧的主梁位移、弯矩和主缆轴力的影响见图4。图4中各指标的变化幅度=吊杆损伤后的静力性能指标-吊杆完好状态下静力性能指标。在图4~图10中,横坐标均采用吊杆编号来表示计算点沿跨度方向的位置,例如:横坐标“9”表示9号吊杆所在位置,后面不再赘述。
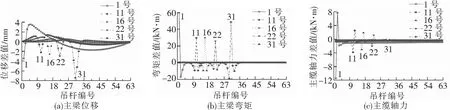
图4 吊杆断裂对关键截面静力性能的影响
由图4可知,1、11、16、22号吊杆断裂均在该吊杆位置使主梁位移、弯矩和主缆轴力发生较大变化,远离该吊杆位置后变化很小,影响范围在该吊杆两侧1~2个吊杆范围内,其中1号边吊杆产生的影响最大。跨中的31号吊杆断裂对跨中主梁位移和弯矩影响较大,但对主缆轴力未产生明显影响。
2.2 吊杆断裂对动力性能的影响
研究表明,构件的局部损伤不会引起自振频率和位移模态的明显变化,但会引起该处结构刚度的变化,从而使模态曲率在损伤处左右会发生突变。位移模态曲率可采用对位移模态进行中心差分得到
(1)
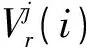
模态曲率可对主梁损伤进行较好的识别[2-4],但模态曲率差(式(2))相较于模态曲率识别效果更好[11]。
(2)
式中,ΔVr(i)为损伤前后第r阶位移模态振型在第i个节点处的模态曲率差绝对值,计算节点均取吊杆与主梁的交点位置。
关键吊杆断裂后前4阶竖向振型的模态曲率差见图5。
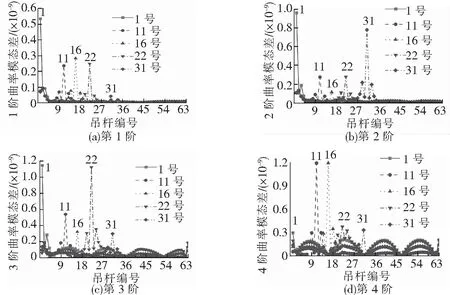
图5 关键吊杆断裂后第1~4阶竖向模态曲率差
由图5可知,在前4阶竖向模态曲率差中,吊杆断裂均在该吊杆位置处引起了明显的突变,且随着模态阶数的增加,突变程度增大,说明模态曲率差对人行悬索桥的吊杆损伤敏感,但不同的模态阶数对不同吊杆的损伤敏感度不同。从图5中也可以看出,模态曲率差除了在损伤吊杆位置有明显突变,在其他位置也有不容忽视的变化,因此若选择该参数进行吊杆的损伤识别,还需进行进一步的研究。
3 吊杆的损伤识别
悬索桥中的吊杆并非隐蔽构件,因此其断裂是可以被及时发现的,比较有意义的是能够在断裂之前对其损伤位置和损伤程度进行识别。以模态曲率差为损伤指标,分别对单根吊杆损伤和多根吊杆损伤等不同的工况进行识别分析。由图5可以看出,吊杆断裂时,虽然在断裂吊杆位置主梁的模态曲率差有明显突起,可以依此识别出损伤吊杆的位置,但在无吊杆损伤位置也有明显的突起,会混淆识别结果。为了减小识别误差,将前m阶模态曲率差绝对值ΔVr(i)进行融合,得到损伤因子DF(Damage Factor)[12]
(3)
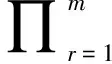
3.1 损伤吊杆位置的识别
3.1.1 单根吊杆损伤时损伤吊杆位置的识别
假设只有一根吊杆发生损伤,其他吊杆均未损伤时,可采用损伤因子DF对单根损伤吊杆的位置进行识别。但由于DF值受损伤程度的影响,不同工况下数值差别较大,故将其归一化,进一步定义节点i处归一化后的损伤判别因子DDF,可表示为
(4)
式中,分母表示同一工况下,1~63根吊杆中DF值的最大值。
由于DDF不受损伤度的影响,故可对任意损伤度下单根损伤吊杆的位置进行识别。当各吊杆损伤程度均为10%时,由不同阶数融合得到的损伤判别因子DDF见图6。
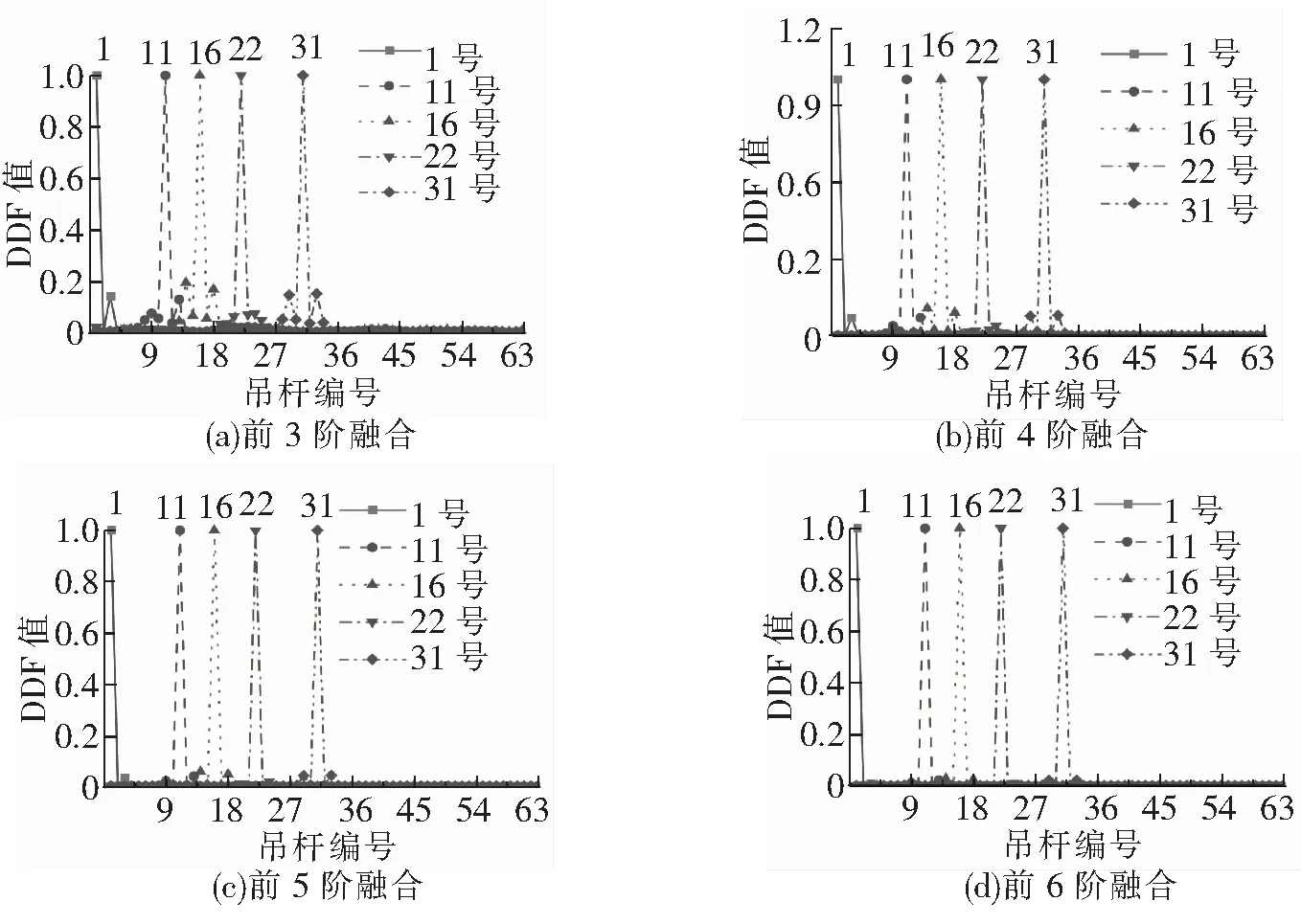
图6 不同阶数融合后的DDF值
由图6可知,损伤吊杆位置的DDF都达到了最大值1.0,可以识别出损伤位置;当融合阶数较少时,除了损伤吊杆位置,在其余无损伤处DDF也出现了较小的峰值,但随着融合阶数的增加,无损伤处DDF峰值的数量和数值都在减小,前5阶融合时,无损处的峰值就已很小,前6阶融合后,则基本消失。
3.1.2 多根吊杆同时损伤时损伤吊杆位置的识别
不同位置的吊杆发生损伤时,在各损伤位置得到的损伤因子DF会出现数量级上的差别。为了对多根吊杆的损伤进行识别,分析各吊杆单独损伤时所对应的损伤因子DF的相对关系。图7给出了各吊杆分别单独损伤10%时,由前6阶模态融合得到的损伤因子DF。由于DF值存在数量级上的差别,难以在同一个图中显示,因此图7中采用分次识别的方式,首先捕获最易识别的损伤吊杆,然后在其后的每一次识别中,都剔除掉上一次已识别出的吊杆,仅对剩余吊杆进行识别。
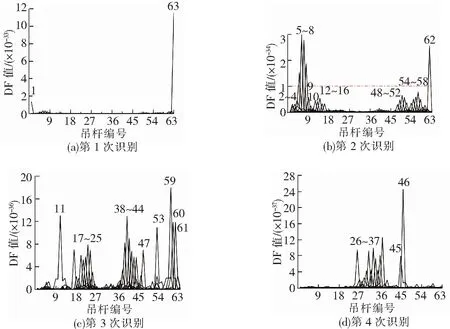
图7 各吊杆单独损伤10%时的识别结果
由图7(a)可知,由于1、63号边吊杆单独损伤时对应的DF值较其他位置吊杆损伤工况大2~6个数量级,是对损伤因子最敏感的区域,因此在第1次识别时即可捕捉;剔除1、63号边吊杆后,图7 (b)的第2次识别结果显示,与1号吊杆较近的2~10号吊杆、12~16号吊杆和右侧的48~52号、54~58号和62号次边吊杆可以明显识别;之后,依次剔除已识别出的吊杆,到图7 (d)第4次时可识别出所有吊杆。由此可见,各吊杆对损伤因子DF的敏感度是不同的,显然边吊杆(图7(a))对损伤因子最敏感,处于很敏感区域;图7 (b)中处于水平线以上的吊杆处于次之的敏感区域,处于水平线以下及图7 (c)中的吊杆处于较敏感区域;图7 (d)中跨中区域的吊杆则处于不敏感区域。总体趋势是,越接近边吊杆位置,对损伤因子越敏感。
在实际结构中,可能存在多根吊杆同时发生损伤,且损伤程度各不相同。由图7可知,如果边吊杆与其他吊杆同时发生损伤,即使采用归一化后的损伤判别因子DDF,由于式(4)中的分母是所有吊杆中DF值的最大值,因此也难以对其他吊杆进行有效识别。在实际的损伤检测中,由于损伤工况是未知的,可首先通过模态测试得到主梁的多阶模态位移,然后结合无损状态下模态位移的数值解(或可用的实测值)进行模态曲率差及损伤因子DF的计算,初步判断不同的敏感区域,再根据DF值的数量级逐层剔除较大值,进行分层次识别。
由于环境因素特别是温度会对桥梁的模态测试结果产生不可忽视的影响,导致损伤识别误判,因此在无损状态下的模态数值分析中,应在计算模型中模拟与现场环境相近的温度荷载,同时建立模态-温度模型来消除温度影响[13-14];如果桥梁在刚成桥时进行了模态测试,则在状态评估时的模态测试也需要选择与成桥测试时相近的温度,以降低温度效应的影响。同时,传感器的数量对模态测试结果也有较大影响[8,15],显然传感器布置越密集,模态曲率的计算越准确,但同时也会使现场测试的工作量增加。由于在模态曲率的计算中取吊杆与主梁的交点为计算点,因此在模态测试时需在每个吊杆位置布置传感器,对于跨径不大的人行悬索桥,采用移动测站法是可以实现的,也可以得到比较准确的模态测试结果。
下面以1、63号(很敏感区域),6号(敏感区域),22、50号(较敏感区域),31、37号(不敏感区域)吊杆同时发生损伤为例来进行分析,分4种损伤工况:工况1,所有吊杆损伤度均为10%;工况2,1、63号吊杆损伤度5%,6号吊杆损伤度10%,22、50号吊杆损伤度15%,31、37号吊杆损伤度20%;工况3,1、63号吊杆损伤度5%,6号吊杆损伤度15%,22、50号吊杆损伤度15%,31、37号吊杆损伤度10%;工况4,仅31、37号吊杆发生损伤,损伤度10%。取前6阶模态进行融合处理,识别结果见图8~图10。
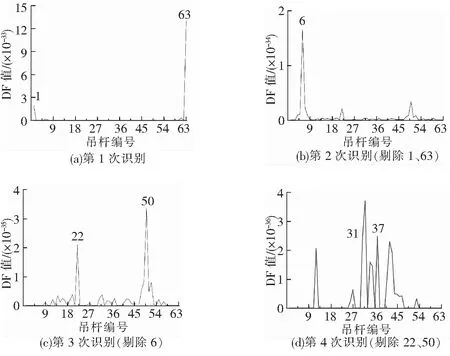
图8 工况1吊杆损伤识别结果

图9 工况2吊杆损伤识别结果
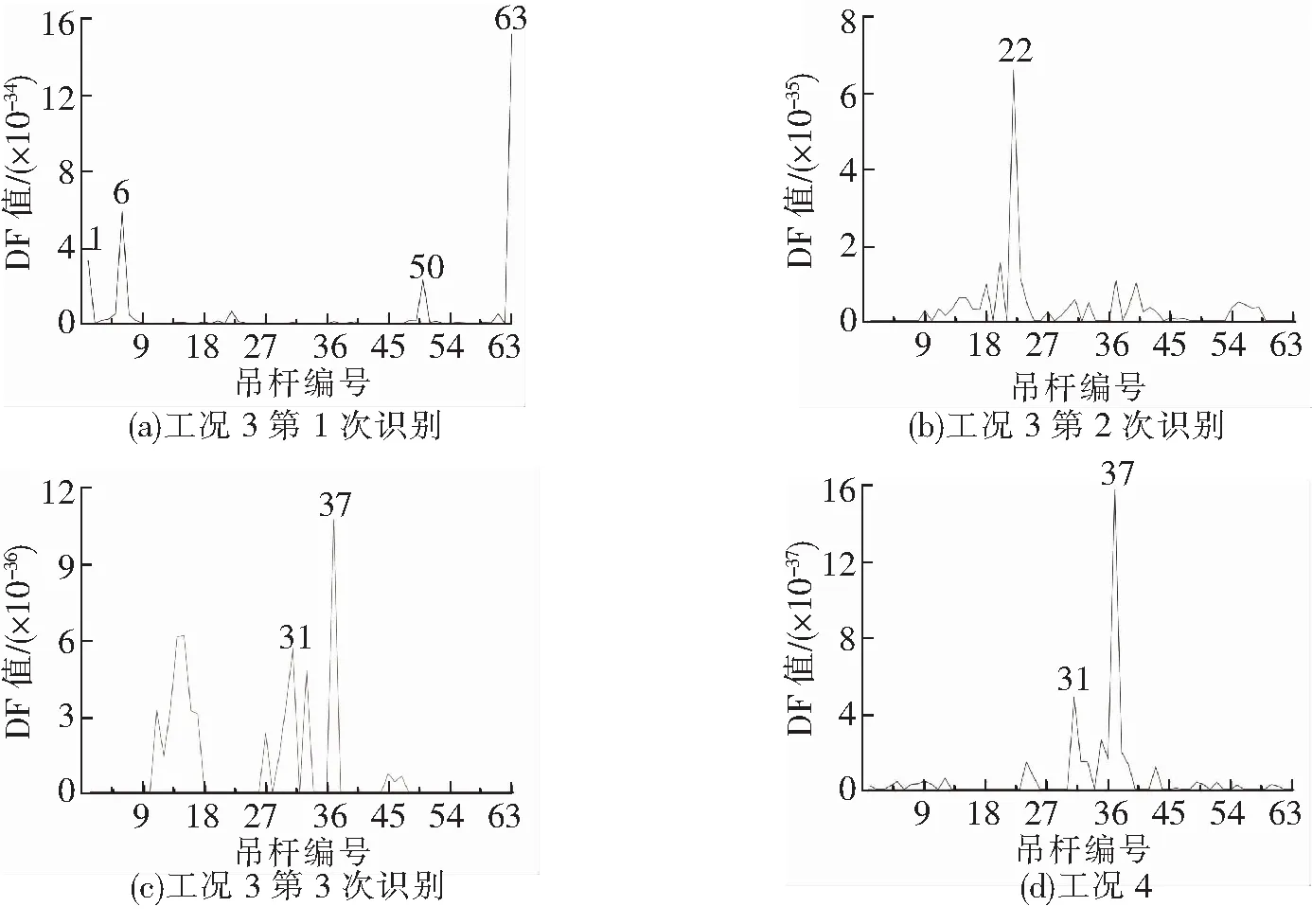
图10 工况3和工况4吊杆损伤识别结果
由图8~图10可知,①各吊杆损伤程度相同时(工况1),很敏感区域图8(a)、敏感区域图8(b)和较敏感区域图8(c)的损伤吊杆位置都很容易识别,但不敏感区域图8(d)受到的干扰较大,较难识别;②当各吊杆的损伤程度不同时(工况2、3),即使很敏感区域的边吊杆损伤程度很小,使DF值下降,仍能较快识别,敏感区域和较敏感区域中,吊杆的损伤度较大,更易识别,例如图9工况2中较敏感区域的50号吊杆比敏感区域的6号吊杆DF值更大,图10工况3中敏感区域的6号吊杆DF值超过了很敏感区域的1号边吊杆,但对于不敏感区域的吊杆,当其损伤度在10%~20%之间时,若有其他区域的吊杆发生损伤,都较难识别;③当只有不敏感区域的吊杆发生损伤时(工况4),在损伤度达到10%时可以识别。
3.2 损伤程度的识别
(1)单根吊杆损伤。当只有单根吊杆损伤时,由3.1节的方法较易识别出其位置,然后针对发生损伤的吊杆,进一步采用损伤因子DF对其损伤程度进行评估。选取1、16、31号吊杆,当各吊杆发生不同程度的单根损伤时,可得到损伤判别因子DF随损伤度变化的关系。鉴于在实际桥梁中吊杆不会出现过高损伤度,因此以损伤度75%时的DF为最大值,定义比值k=DF/DF75%,得到k与损伤度的关系,并进行公式拟合,见图11。根据图11中损伤度与比值k的关系,则可针对某单根损伤吊杆的实际DF值确定其损伤度。
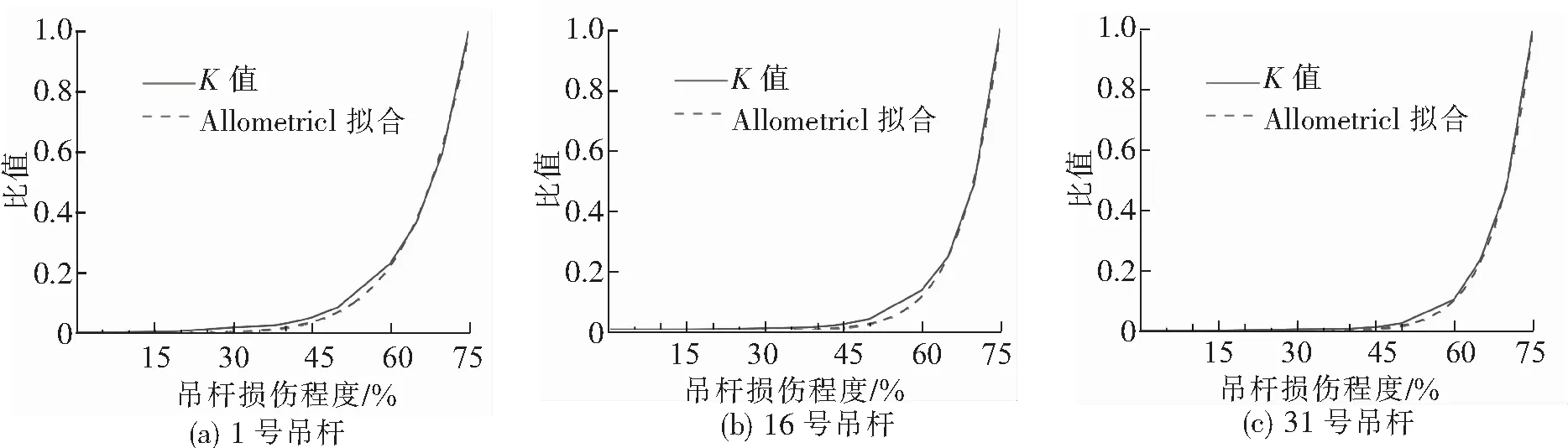
图11 单根吊杆损伤度与比值k的关系
(2)多根吊杆同时损伤。当多根吊杆同时损伤时,各吊杆之间的DF值会相互影响。观察图8~图10,由于损伤组合工况不同,即使同一根吊杆损伤程度相同,其在不同工况中的DF值也不相同,例如当6号吊杆损伤10%时,在工况1中DF为1.6×10-34,而在工况2中为6×10-35,因此采用DF值难以在多根吊杆同时损伤时评估吊杆的损伤程度。通过计算发现,除边吊杆外,其余吊杆在损伤度8%以下都较难识别,由于在实际桥梁中拉索断丝率达到10%就需要进行更换[16],因此除边吊杆外,只要能采用DF法有效识别出来的,就说明已达到吊杆更换标准。
4 结论
针对人行悬索桥分析了吊杆损伤和断裂对桥梁受力性能的影响,并基于模态分析,研究了不同的模态参数对吊杆损伤识别的适用性。研究结果表明:
(1)吊杆损伤对其索力的影响很小。随着吊杆损伤程度的增加,损伤吊杆的应力增大,但仅局限在该损伤吊杆本身,只要吊杆未发生断裂,相邻吊杆的应力就基本不发生变化。吊杆断裂对其相邻吊杆的应力影响最大,边吊杆和跨中吊杆的断裂对相邻吊杆应力产生的影响大于1/4跨区域内吊杆断裂的影响。
(2)吊杆断裂在该吊杆位置使主梁位移、弯矩和主缆轴力发生较大变化,远离该吊杆位置后变化很小,影响范围在该吊杆两侧1~2个吊杆范围内。
(3)模态曲率差对人行悬索桥的吊杆损伤敏感,但不同的模态阶数对不同吊杆的损伤敏感度不同。对模态曲率差进行多阶融合后得到的损伤因子DF及其归一化参数DDF可对单根吊杆损伤时的损伤吊杆位置进行有效识别。
(4)多根吊杆同时发生损伤时,可首先通过模态测试得到主梁的多阶模态位移,然后结合无损状态下模态位移的数值解或实测值进行模态曲率差及损伤因子DF的计算,初步判断不同的敏感区域,再根据DF值的数量级逐层剔除较大值,进行分层次识别。
(5)单根吊杆损伤时其损伤程度可通过比对已知损伤度下的DF值进行评估;多根吊杆同时损伤时可根据DF法的有效识别结果判定其是否达到吊杆更换标准。
