自锚式悬索桥损伤吊索系统拉力重分布研究

2021-02-26李文武周洋陈鹏飞叶毅

铁道科学与工程学报 2021年1期

李文武，周洋，陈鹏飞，叶毅

自锚式悬索桥损伤吊索系统拉力重分布研究

李文武1，周洋1，陈鹏飞2，叶毅2

(1. 湖南省交通规划勘察设计院有限公司，湖南长沙 410200；2. 西安建筑科技大学土木工程学院，陕西西安 710055)

为研究吊索损伤对自锚式悬索桥吊索系统内力的影响机理，以某主跨160 m的混凝土自锚式悬索桥为工程依托，采用非线性静力分析方法，对吊索不同损伤程度下结构的力学响应进行研究。研究结果表明：吊索损伤引起吊索系统的拉力重分布，主要发生在损伤吊索和与之同跨同侧相邻的2根吊索之间，具有相邻性；相较于单根吊索损伤，相邻2根吊索发生损伤后结构的力学响应更为剧烈，且与这2根吊索分别发生损伤引起同侧吊索拉力重分布的叠加效果几乎等效。研究结果可用于自锚式悬索桥损伤索力控制，同时可为损伤吊索监测提供技术指导。

自锚式悬索桥；吊索损伤；吊索系统；拉力重分布

吊索作为自锚式悬索桥的关键构件，将作用于桥面系上的荷载传递给主缆等主要受力构件。桥梁运营期间，吊索容易因锈蚀发生损伤[1]。近年来，已发生多起因吊索损伤引起的桥梁安全事故[2]。吊索材料多采用平行钢丝束或钢绞线，其中部分钢丝的断裂便会造成整根吊索的抗拉刚度减小，从而引起吊索系统的拉力重分布，危及桥梁结构的安全[3]。因此，研究损伤吊索系统的拉力重分布规律具有必要性。CAI等[4]通过研究拉索损伤断裂引起的斜拉桥非线性反应和破坏，发现单根拉索发生破断对其他拉索的拉力影响较小，但相邻2根拉索同时发生断裂会导致其他拉索屈服。夏欢等[5]针对中承式拱桥吊杆发生不同程度损伤时，剩余吊索的力学行为进行研究，发现吊索损伤对剩余吊索拉力的影响具有相邻性。朱劲松等[6]对中承式拱桥体系冗余度进行了分析，发现一般吊杆或长吊杆的破断对结构影响最为显著，可导致其极限承载能力降低约30%。自锚式悬索桥在实际工程中已经逐步被应用，然而，吊索损伤对吊索系统的拉力重分布特征还未开展广泛研究。为此，本文以一座主跨160 m的自锚式悬索桥为工程依托，运用非线性静力分析方法，研究不同吊索损伤情况下吊索系统拉力重分布特征，为该类型桥梁的运营和养护提供依据，同时也为该类型桥梁的吊索更换提供理论指导。

1 吊索损伤模拟与拉力计算

吊索的损伤均被认为是某一根或多根钢丝(钢绞线)断裂失效，且断裂失效的钢丝与完好的钢丝之间没有约束，而断裂的钢丝或钢绞线整根不再受力[7]。因此，吊索的损伤程度可通过改变吊索有效抗拉面积来模拟[8-9]。吊索的初始横截面面积为A,0，损伤后吊索的横截面积为A,=(1−)A,0，其中，变量表示吊索的损伤程度：

规定吊索的初始长度为L,0，初始轴力为N,0，初始伸长ΔL,0，吊索引起的锚固点间距离变化为Δ|0|，则在吊索锚固点上存在力的平衡条件：

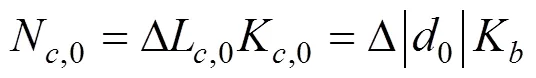
式中：K,0表示吊索的初始刚度；K表示桥梁除损伤吊索外的剩余部分相对锚固点之间距离增量的刚度。吊索的损伤会致使其抗拉刚度减小K,0，长度相应增大Δ，因此损伤吊索的总伸长为(ΔL,0+Δ)。根据吊索总伸长与锚固点之间的距离增量相协调，可知：

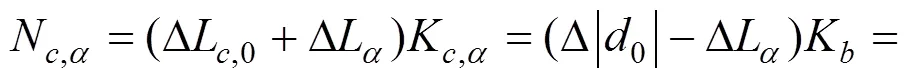
2 工程概况

3 吊索损伤非线性静力计算模拟

全桥三维有限元模型采用ANSYS建立，主梁和索塔选用beam4单元，主缆和吊索选用link10单元，如图2所示。模型中主梁以鱼刺梁的形式模拟，纵向主刺的截面特性按主梁的实际截面特性取值；主刺两侧为刚臂，起到传递荷载的作用，用来模拟主梁和吊索的连接；吊索和主缆初始应力的施加通过赋值初应变实现；索塔底部采用固结形式约束。

单位：mm

图2 自锚式悬索桥有限元模型

不论平行钢丝束吊索还是钢绞线吊索，吊索的损伤均可理解为某一根或多根钢丝(钢绞线)断裂失效，且断裂失效的钢丝(钢绞线)与完好的钢丝(钢绞线)之间没有约束，断裂的钢丝或钢绞线整根不再受力。因此，吊索的损伤程度可通过调整吊索有效抗拉面积A的变化来模拟。本文将单根吊索损伤分为20%，40%，60%和80% 4个程度，分析不同损伤程度下吊索静拉力的变化规律。

4 不同吊索损伤工况引起的吊索拉力重分布特征分析

4.1 单根吊索不同程度损伤引起吊索拉力的重分布

为初步了解吊索损伤对自锚式悬索桥吊索系统的影响[10]，先对中跨L28号吊索进行分析，研究该吊索发生不同损伤程度后结构的力学行为。图3给出了L28号吊索发生不同程度的损伤时各吊索拉力的变化情况。L28号吊索的损伤程度由0增加至80%，拉力值非线性减小，最大降幅达到553.40 kN；而L27号、L29号吊索的拉力不断增加，最大增加均为260.10 kN左右；L26号、L30号吊索的拉力同样逐渐增加但增幅较小，最大仅有14.10 kN；同侧其他吊索的拉力则没有明显的变化；另一侧吊索中，只有R27号、R28号和R29号吊索的拉力发生了变化，且变化数值最大值未超过4.00 kN，仅占成桥状态下吊索拉力的1%。可认为吊索损伤主要引起该吊索及其同侧相邻2和3根吊索的拉力发生变化，而对其他吊索拉力的影响很小，且损伤吊索的拉力减小值主要转移至与其紧邻吊索，其余吊索分担的拉力值呈现随着与损伤吊索距离的增加而减小的趋势。

对比图3和图4，不难发现L28号吊索发生不同程度的损伤时，L28号吊索及其同侧相邻2和3根吊索的应力均有所增长。L28号吊索的损伤率由0增加至80%，L28号吊索承受的应力由397.89 MPa增大至1 395.00 MPa，吊索应力增加了2.51倍已接近其材料的屈服应力1 420 MPa，此时该吊索已处于容易发生破断的状态。而此时吊索有效抗拉面积仅为无损状态的20%，因此相较于发生损伤前，L28号吊索的拉力减少了553.40 kN。说明局部损伤引起吊索有效抗拉截面面积的减小，会导致损伤吊索应力的剧烈增加，但吊索拉力会减小。

随着L28号吊索的损伤率由0%增加至80%，与其相邻的L27号、L29号吊索的应力也有较为明显的增长，增幅可以达到14.00%；然而，L26号、L30号吊索应力的增长则十分有限，均不足1%。可见当某根吊索发生损伤时，与其相邻吊索的拉力和应力均会有所增长，且增长的幅度随着与损伤吊索距离的增加而减小，说明吊索破断对剩余吊索拉力的影响具有相邻性。

单位：kN

4.2 不同位置处吊索损伤对吊索拉力重分布的影响

为进一步研究吊索损伤对吊索系统内力重分布的影响，依据吊索所处位置不同分别选取L6号，L9号，L12号，L13号，L20号和L28号等吊索作为损伤吊索，计算各工况下该损伤吊索及其同侧相邻2根吊索的拉力变化量情况。

由图5可知，在吊索未发生损伤时，桥塔两侧吊索L12号、L13号拉力略小，其余各吊索的拉力均约等于1 800.00 kN。随着吊索损伤率的增加，各损伤吊索的拉力均呈减少的趋势，但各吊索拉力减少的幅度各有不同。吊索损伤率由0%增加至80%，桥塔两侧L12号、L13号吊索的拉力分别减少67.38%和66.87%，边跨跨中L6号吊索的拉力减少51.42%，边跨近桥塔1/4处L9号吊索的拉力减少60.12%，中跨近桥塔1/4处L20号吊索的拉力减少46.72%，中跨跨中L28号吊索的拉力减少29.86%。可见，吊索越靠近桥塔，则该吊索发生损伤时拉力损失的越多。

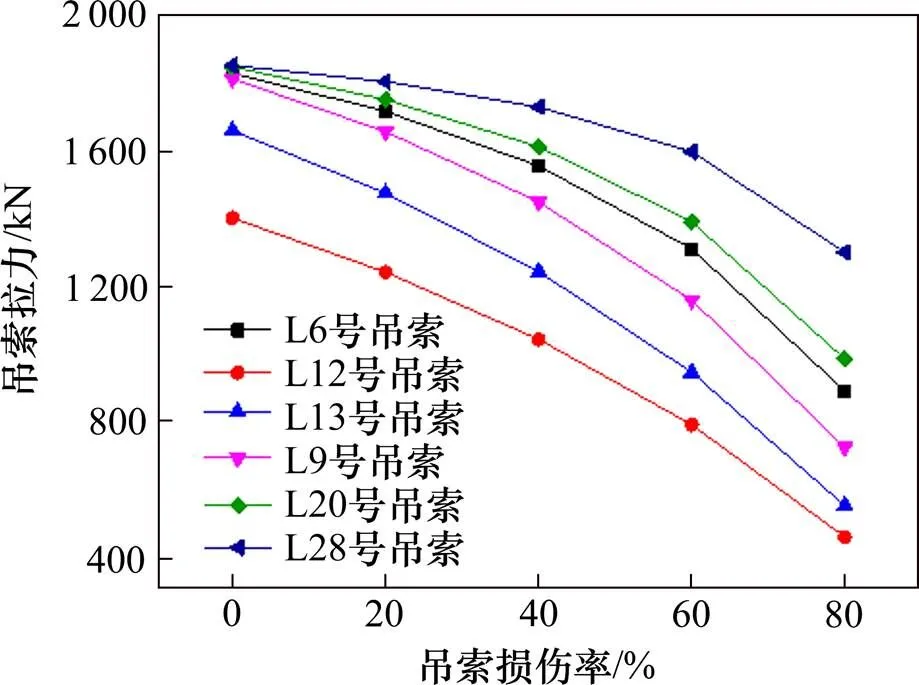
单位：kN

图6说明不同位置吊索发生相同程度的损伤时，与其相邻吊索的拉力增加幅度不同。以各吊索的损伤程度均由0%达到80%为例，与L6号吊索相邻L5号吊索拉力的增长率为22.61%，与L28号吊索相邻L27号吊索拉力的增长率却只有14.10%，而与L20号吊索相邻L19号吊索拉力的增长率19.82%，居于两者之间。说明吊索越靠近桥塔，则发生损伤时与其相邻吊索的拉力就增加越多。对比图7与图6，L12号吊索的损伤率由0%增加至80%时，与之同侧的L11号吊索拉力的增长率为17.33%，与之不同侧的L13号吊索拉力的增长率仅1.43%。而L13号吊索的损伤率达到80%时，L12号与L14号吊索拉力的增长率同样存在类似的差异。可见，由于桥塔的存在，吊索损伤主要引起与之同跨吊索的拉力发生变化，而对另一跨吊索拉力的影响较小。

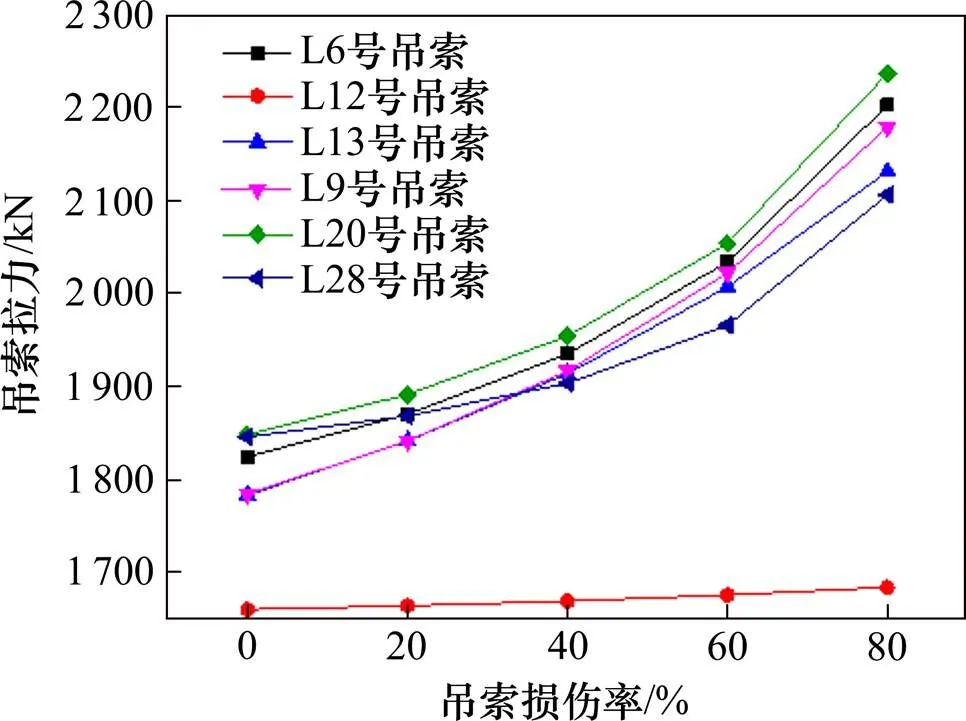
单位：kN

综合图5至图7，不难发现，吊索发生损伤时桥塔会影响吊索拉力的重分布，同时，吊索损伤主要是引起吊索拉力变化，竖向荷载重分布的传递主要通过吊索、主缆作用于桥塔，最后传递给基础。因此，吊索损伤引起的竖向荷载变化会随着与桥塔距离的不同，不同程度的通过桥塔传递给基础，而传递至另一跨吊索的拉力值均较小，因而在吊索发生损伤后应着重关注与之同侧紧邻吊索的状态。

图8将不同吊索在发生不同程度损伤时，与损伤吊索相邻2根吊索的拉力变化值进行了比较。无论吊索的损伤程度如何，与其同侧相邻2根吊索的拉力增加量之间始终存在一定的倍数关系。可见，当某根吊索发生损伤时，与其左右相邻吊索拉力增加值的比值，是和吊索本身特性相关的一个恒定值，如吊索长度等。不难发现，相对长度较短吊索的拉力增加值总是比相对长度较长吊索的拉力增加值更大(ΔL5＞ΔL7，ΔL8＞ΔL10，ΔL22＞ΔL20)，而相对长度相同的L27号、L29号吊索的拉力增加值则几乎相等。当某根吊索发生损伤时，在与其相邻的2根吊索中，长度较短那根吊索的拉力增长更多。

图8 Li-1号与Li+1号吊索拉力变化值的比值

表1和2将与损伤吊索相邻吊索的拉力增加值和损伤吊索的拉力减小值进行了对比。L6号，L20号和L28号吊索不论发生何种程度损伤，与其同侧相邻2根吊索拉力的增加量之和，均大于其拉力减少量的84.08%。对于这些吊索，拉力重分布主要发生在损伤吊索和与其紧邻的2根吊索之间。对L12号吊索进行分析，各损伤工况下，与其同侧同跨相邻L11号吊索的拉力增加量均占其拉力减小量的30.86%左右，L10号吊索的拉力增加量仅占其拉力减小量的9.37%左右，而与之不同侧L13号和L14号吊索的拉力增长率则均不足3%。对L13号吊索进行分析，同样只有L14号吊索的拉力发生了较为明显的变化。可见，桥塔侧吊索发生损伤时，拉力重分布同样仅发生在损伤吊索和与其紧邻的吊索之间。由于桥塔等参与了力的分配，桥塔侧吊索发生损伤，仅引起与之同跨吊索的拉力显著增加，另一跨吊索的拉力受影响很小。

表1 不同损伤工况下Li-1号和Li+1号吊索拉力变化矢量和占Li号吊索拉力变化量的比例

表2 L12号吊索发生不同程度损伤时，部分吊索拉力变化值和L12号吊索拉力减少量的比例

单位：MPa

图9给出了各吊索发生不同程度的损伤时锚固端主缆拉力变化值。可知，不同位置的吊索发生损伤引起的主缆拉应力变化值均不相同，且随着吊索损伤程度的增大锚固端主缆拉应力变化值亦会增大，但各位置吊索损伤引起的主缆锚固端拉应力变化值均小于1 MPa。因此，吊索损伤虽会引起主缆拉应力发生变化，但其变化幅值很小，可判定吊索损伤对主缆拉应力的影响甚微。

4.3 多根吊索损伤缆索系统内力重分布

实际工程中容易出现多根吊索同时存在不同程度损伤的情况，因此有必要针对多根吊索损伤时吊索系统的内力重分布进行研究。多根吊索同时存在损伤，对结构的影响存在交叉相互作用，吊索的拉力分布相较于单根损伤也就更为复杂。为此设定如下工况，进行多根吊索损伤时剩余吊索内力响应的分析。

工况1：L28号吊索损伤程度达到20%；

工况2：L29号吊索损伤程度达到60%；

工况3：L30号吊索损伤程度达到60%；

工况4：L28号吊索损伤程度达到20%，且L29号吊索损伤程度达到60%；

工况5：L28号吊索损伤程度达到60%，且L29号吊索损伤程度达到20%；

工况6：L28号吊索损伤程度达到20%，且L30号吊索损伤程度达到60%；

工况7：L28号吊索损伤程度达到20%，且R28号吊索损伤程度达到20%。

针对各工况进行分析时，假设悬索桥处于合理成桥状态，有且仅有工况设定吊索发生相应的损伤，记录吊索拉力的变化值如表3所示。

表3 不同损伤工况下部分吊索拉力的变化值

工况1～3说明，单根吊索发生损伤时，该吊索的拉力减小，与其相邻的2根吊索拉力增大，其他吊索的拉力则几乎没有变化；工况4～5说明，同侧相邻2根发生损伤，同样仅对与其相邻的2根吊索拉力有影响，对其他吊索拉力的影响甚微；工况7说明，不同侧的两根吊索发生损伤，对与2根损伤分别相邻的4根吊索拉力均有影响，对其他吊索同样影响甚微。

从表3可知，工况4中L29号吊索的拉力减小了238.9 kN，而该吊索在工况1和2中拉力变化值的矢量和为237.0 kN，两者大致相等。对比工况1，3和6，发现工况6引起各吊索拉力的变化值，与工况1和工况3分别引起同号吊索拉力变化值的矢量和同样是相等的。说明某2根吊索发生损伤引起同侧吊索拉力的重新分布，与这2根吊索分别损伤引起同侧吊索拉力重分布的叠加效果几乎是等效的。

对比工况5和4，当L28号吊索的损伤程度大于L29号吊索时，L27号吊索的拉力变化值为122.9 kN大于L39号吊索的拉力变化值31.0 kN；而当L28号吊索的损伤程度小于L29号吊索时，L27号吊索的拉力变化值为30.7 kN，亦小于L30号吊索的拉力变化值124.1 kN。说明2根吊索发生损伤时，与受损程度相对严重吊索接近的那根吊索拉力的增大值更高，受影响更大。2根相邻吊索损伤时，损伤小的吊索其拉力也增大，使得吊索应力大幅增加，风险相应增加。

5 结论

1) 吊索发生损伤后吊索系统进行内力重分布，对剩余吊索拉力的影响具有相邻性，增长的幅度随着与损伤吊索距离的增加而减小。

2) 靠近桥塔吊索，吊索发生损伤引起与之同跨吊索拉力显著增加，另一跨吊索拉力受影响较小。

3) 吊索发生损伤引起的主缆拉应力发生变化微乎其微。

4) 2根吊索发生损伤引起同侧吊索拉力的重分布，与这2根吊索分别损伤引起同侧吊索拉力重分布的叠加效果几乎等效。

5) 2根吊索发生损伤，受损程度相对严重的吊索，周边吊索拉力的增大值也相对更高，受吊索损伤影响更大。受损程度小的吊索拉力也增大，吊索应力大幅增大，在实际养护中应予以关注。

[1] Yukari Aoki, Hamid Valipour, Bijan Samali. A study on the progressive collapse responses of cable-stayed bridges[J]. Advances in Structure Engineering, 2013, 16(4): 689−706.

[2] 陈宝春, 范冰辉, 余印根, 等. 钢管混凝土拱桥强健性设计[J]. 桥梁建设, 2016, 46(6): 88−93. CHEN Baochun, FAN Binghui, YU Yingen, et al. Robust design of CFST arch bridge[J]. Bridge Construction, 2016, 46(6): 88−93.

[3] 李红松. 钢丝损伤对悬索桥吊索承载力影响分析[D]. 阜新: 辽宁工程技术大学, 2015. LI Hongsong. Analysis of the influence of steel wire damage on the sling bearing capacity of suspension bridge[D]. Fuxin: Liaoning University of Engineering and Technology, 2015.

[4] CAI J G, XU Y X, ZHUANG L P, et al. Comparison of various procedures for progressive collapse analysis of cable-stayed bridges[J]. Journal of Zhejiang University- Science A (Applied Physics & Engineering), 2012, 13(5): 323−334.

[5] 夏欢, 金晓勤, 晏班夫. 拱桥在役损伤吊杆破断安全性研究[J]. 中外公路, 2017, 37(1): 98−102. XIA Huan, JIN Xiaoqin, YAN Banfu. Study on the safety of in-service damaged suspenders of arch bridges[J]. Sino Foreign Highway, 2017, 37(1): 98−102.

[6] 朱劲松, 盛荣荣. 中承式系杆拱桥体系冗余度分析[J]. 重庆交通大学学报(自然科学版), 2018, 37(7): 1−8. ZHU Jinsong, SHENG Rongrong. Redundancy analysis of the tied arch bridge system[J]. Journal of Chongqing Jiaotong University (Natural Science Edition), 2018, 37(7): 1−8.

[7] 赵翔. 拉索损伤对斜拉桥结构性能影响的研究[D]. 南京: 东南大学, 2005. ZHAO Xiang. Study on the influence of cable damage on the structural performance of cable-stayed bridge[D]. Nanjing: Southeast University, 2005.

[8] 李晓章, 谢旭, 潘骁宇. 拱桥吊杆锈蚀高强钢丝疲劳性能试验研究[J]. 土木工程学报, 2015, 48(11): 68−76. LI Xiaozhang, XIE Xu, PAN Xiaoyu. Experimental study on fatigue performance of corroded high tensile steel wires of arch bridge hangers[J]. Journal of Civil Engineering, 2015, 48(11): 68−76.

[9] Ruiz-Teran A M , Aparicio A C . Response of under-deck cable-stayed bridges to the accidental breakage of stay cables[J]. Engineering Structures, 2009, 31(7): 1425− 1434.

[10] 邱文亮, 吴广润, 张哲. 突然断索后双吊索形式自锚式悬索桥安全分析[J]. 大连理工大学学报, 2016, 56(6): 600−607. QIU Wenliang, WU Guangrun, ZHANG Zhe, et al. Safety analysis of double sling self anchored suspension bridge after sudden cable break[J]. Journal of Dalian University of Technology, 2016, 56(6): 600−607.

Study of internal force redistribution of damaged hanger system of self-anchored suspension bridge

LI Wenwu1, ZHOU Yang1, CHEN Pengfei2, YE Yi2

(1. Hunan Provincial Communications Planning, Survey & Design Institute Co., Ltd., Changsha 410200, China; 2. School of Civil Engineering, Xi’an University of Architecture & Technology, Xi’an 710055, China)

In order to study the mechanism of the influence of hanger damage on the internal force of the self-anchored suspension bridge hanger system, a concrete self-anchored suspension bridge with a main span of 160m was taken as an example. The nonlinear static analysis method was used to study the mechanics of the structure under different damage degrees of the hanger. The response was analyzed. The results show that the hanger damage causes the redistribution of the tension of the hanger system, which mainly occurs between the hanger and the two hangers adjacent to the same side of the hanger, with adjacency. Compared with the single hanger, in the damage, the mechanical response of the structure is more severe after the damage of two adjacent hangers, and the superposition effect of the two hangers respectively causing the damage of the same side hanger tensile force is almost equivalent. The research content can be used to control the damaged cable force of self-anchored suspension bridge and provide technical guidance for the monitoring of damaged sling.

self-anchored suspension bridge; hanger damage; hanger system; internal force redistribution