质子交换膜燃料电池单电池振动响应分析

温小飞，陈泽滔，詹志刚，邱 阳

(1.浙江海洋大学船舶与海运学院，浙江舟山 316022；2.武汉理工大学材料复合新技术国家重点实验室，湖北武汉 430070)

质子交换膜燃料电池(PEMFC)是目前应用最广泛的燃料电池之一，具有能量转换率高、工作温度低、污染低、噪音低等优点，在新能源领域受到极大的关注。目前燃料电池已用于汽车、客车、有轨电车等交通工具，在运输行驶过程中由于路面不平、悬架系统和车轮滚动等影响将不可避免的产生振动，这些振动将对燃料电池产生复杂的影响，如膜电极组件受到的夹紧力减小、气密性降低、电阻增加以及结构损坏和断裂等[1-3]。在燃料电池的长期运行过程中，不接近谐振频率或自然频率的频率对整体性能的影响很小，但当工作频率范围接近谐振频率范围时，外部振动频率接近燃料电池自身的固有频率则会产生高振幅共振振动，这会引起燃料电池组件的损坏以及运行性能的下降，从而影响使用寿命。因此，识别燃料电池的固有频率以免引起共振具有重要的意义。刘博等[4]基于有限元法对PEMFC 堆进行了模态分析，从叠层整体模态中分辨出局部振动，预测其变形的形状和方向，并讨论夹持结构和夹持力大小对振动模态的影响。Sangkeun Ahn等[5]通过冲击试验测量了PEMFC 的振动模态特性，以确定影响燃料电池耐久性的主要模态，通过比较燃料电池汽车的加速度和车内噪声，确定了主要响应的频率范围，分析了在此频率影响下PEMFC 的振型。Ahmed 等[6]利用Mindlin 的板理论和有限元模型计算了PEMFC 的固有频率和模态振型，讨论了单电池各组件的厚度、杨氏模量和密度的改变对PEMFC固有频率的影响，但他们将PEMFC 结构简化转换成复合材料板，忽略了双极板气体流道和垫圈对其造成的影响。本文在此基础上完整建立了单电池的有限元模型，利用有限元分析软件[7]对单电池的模态和振动特性进行了计算，并分析其动态响应结果，为避免引起共振和以后的结构优化设计提供依据。

1 有限元模型的建立

1.1 结构及材料参数

电池单元由不同的部件组成，包含两个双极板、两个GDL(气体扩散层)、MEA(质子交换膜)和密封件，其模型见图1。石墨双极板尺寸为187 mm×102 mm×2 mm，其上有加工蛇形流道，槽深1 mm，流道肋与GDL 接触用于传递电流，流道槽用于燃气流通。厚度为50 μm 的Nafion 膜夹在一对作为气体扩散层厚度为200 μm 的碳纸之间形成膜电极组件。密封圈材料为聚四氟乙烯(PTFE)，两层厚度累积为450 μm，它有助于密封燃料和氧化剂周围的活动区域。所有组件之间没有缝隙，因此在分析过程中，接触是连续的。材料参数见表1。

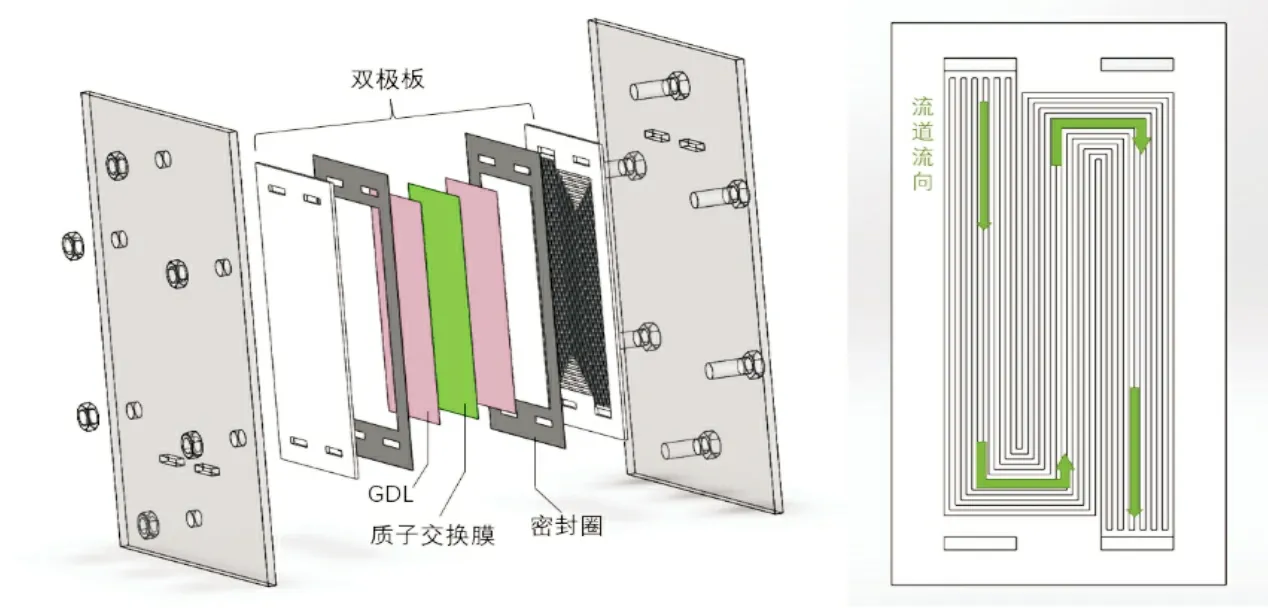
图1 单电池叠组件示意图和双极板流道

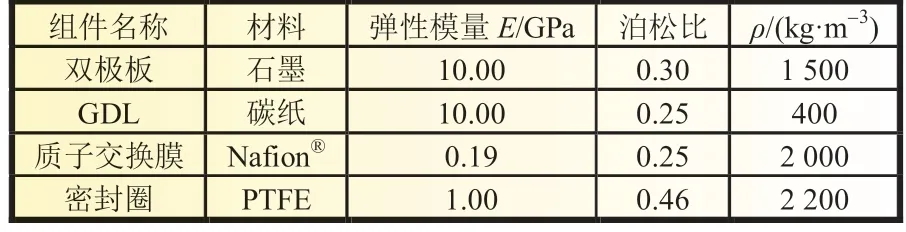
表1 单电池各组件材料参数[6]

1.2 有限元模型

有限元分析的结果很大程度取决于有限元模型的建模精度和网格划分，模型精度的高低决定了分析结果的应用价值，网格划分的质量则影响计算结果的精度和效率。网格划分越精细，计算结果精度越高，但所需要的分析时间也就相应变长。因此，网格要合理划分，对于精度要求较高的部件，则应加大网格密度；对精度要求较低的部件，则应减小网格密度，从而在保证计算精度的前提下提高分析效率。

考虑到MEA 部件相比整体来说厚度太薄，故需要单独对MEA 划分网格，采用平面网格划分法并加大对MEA 的网格密度。双极板的流道出入口处厚度相对于整体而言较薄，可能会在模态分析中产生较大的振幅，因此对其周围进行了网格加密，来提高结果精度。利用系统智能划分法进行网格划分，其中MEA 部件、GDL 部件和密封圈部件生成的网格单元为六面体，而双极板由于内侧流道的存在，生成的网格单元为四面体。最终网格划分生成239 398 个单元，得到485 708 个节点，单元质量平均值为0.76，大于0.7，符合分析要求(其值处于0 和1 之间，0 为最差，1 为最好)。单电池网格划分后的有限元模型见图2。

图2 单电池总体网格划分

1.3 接触方式

单电池的各个组件之间的接触需要定义合适的约束，如密封圈与双极板之间为了防止在振动分析中发生切向分离，需要将其接触设为粗糙。同理，流场板与GDL、GDL 与催化层、催化层与质子交换膜之间，均设置接触为粗糙约束，其他面之间的接触类型设为绑定。

2 模态分析

模态分析是动力学频域分析的基础，通过结构的特征激励响应并进行傅里叶变换，获取物件结构任意两点之间存在的机械导纳函数，归纳出结构的模态参数和振动响应特性，能够用来计算物件结构的振动频率和振动形态，因此也可以叫做频率分析或振型分析。

在模态分析过程中，电池结构的自由振动方程可以表示为：

式中：M为质量矩阵；K为刚度矩阵；u为位移。位移u的通解可以由各阶模态的线性组合表示[8]:

式中：φn为结构第n阶的振动模态；qn为系数，其可通过初始条件求解获得；fn为结构第n阶的固有频率[4]。

将单电池的四边进行固定支撑约束，在计算模块中设置模态求解阶数为6，计算得到的固有频率见表2。

表2 单电池前6 阶固有频率

由于单电池在工作环境中受到的外部激振与单电池的某个固有频率相近乃至相同时会产生共振，进而使得单电池某处的振幅较大。这因共振影响较大的区域为单电池相对薄弱之处，我们可以以此为基础来对单电池进行结构优化，使其固有频率避开工作环境频率，避免共振破坏单电池结构。单电池相应振型图见图3。

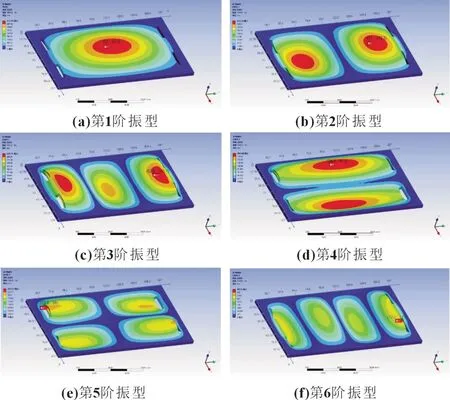
图3 单电池模态前6阶振型图

有限元中模态分析的本质是求矩阵的特征值问题，所以“阶数”就是指特征值的个数，将特征值从小到大排列就是阶次。实际的分析对象是无限维的，所以其模态具有无穷阶，一般对于运动起主导作用为前几阶模态，结合本文研究对象问题故仅对单电池前6 阶模态进行分析及讨论。通过求解方案信息得知，单电池第1 阶固有频率为1 055.9 Hz，振型为从中间部分开始沿Z轴方向摆动且绕Y轴扭转；第2 阶固有频率为1 344.8 Hz，振型为从中部开始绕X轴扭转；第3 阶固有频率为1 823.4 Hz，振型为从中部开始绕X轴弯曲；第4 阶固有频率为2 288.5 Hz，振型为整体向X轴方向摆动，但因其四周固定而呈现出绕Y轴扭转的现象；第5 阶固有频率为2 503.8 Hz，振型为从中部开始绕Z轴扭转；第6 阶固有频率为2 519.8 Hz，整体向Y轴方向摆动，但因其四周固定而呈现出绕X 轴扭转的现象。从图3 可以看出单电池容易出现振动的部位主要集中在中部和气体出入口周围，且气体出入口四周的变形量要高于中部。由此可知，气体出入口周围为单电池的薄弱部位。

3 谐响应分析

谐响应分析是确定一个线性结构在已知频率的正弦(简谐)载荷作用下结构响应的技术，通过对线性系统施加一系列不同频率的周期正弦激励，分析其在周期激励下的周期响应(稳态响应)，即不考虑激励刚开始加入系统时候的瞬态响应。

在谐响应分析中，电池结构的基本依据是动力学方程：

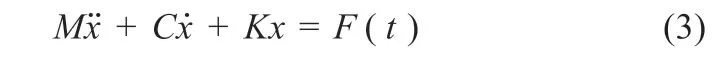
式中：C为结构的阻尼矩阵；F(t)为随时间变化的载荷系数。位移x和F(t)均为简谐量，表示为：

将式(4)和(5)中的x两次求导，并代入式(3)，得到谐响应分析运动方程为：

式中：F1、F2为激振力。

在获得单电池模态分析结果的基础上，采用模态叠加法对单电池进行谐响应分析。在进行谐响应分析之前，需要设置响应频率的范围，根据前6 阶模态分析频率设定频率范围为0～3 000 Hz、步长为30 Hz 间隔。根据燃料电池堆的性能参数，螺栓上的总扭矩为20 Nm，计算可得螺栓预紧力为12 820 N。根据单电池的实际工作状况，在两双极板表面分别加载Z轴方向向内12 820 N 的正弦激励。选取垂直于Z轴的双极板外表面分析单电池的振动响应，利用有限元分析软件中的谐响应模块计算得到单电池在Z方向上的位移、速度和加速度的谐响应分析结果，其结果如图4 所示。

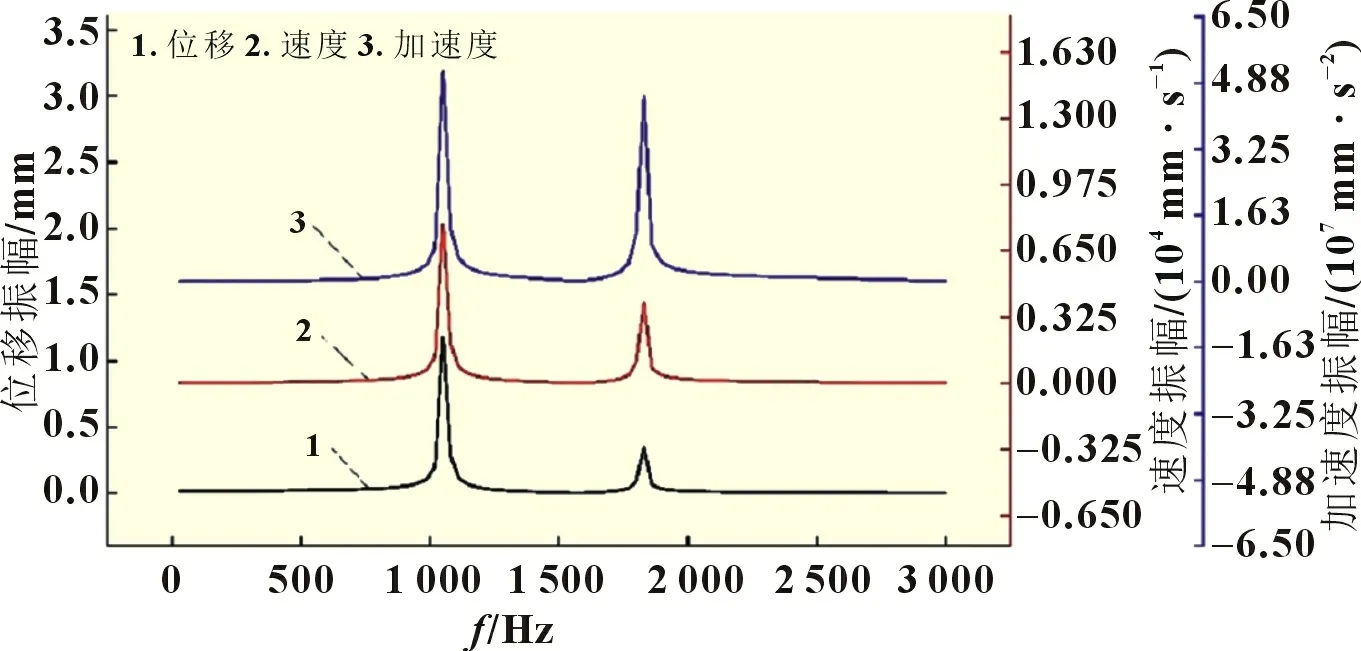
图4 单电池Z方向位移、速度、加速度频率曲线

根据得到的数据分析，在单电池Z方向上的位移、速度和加速度频率响应曲线基本处于相同趋势，当频率处于1 050和1 860 Hz 时，频率幅值有着明显的剧增，且位移、速度、加速度幅值都在1 050 Hz 时达到最大值，分别是1.18 mm、7.79×103mm/s 和5.14×107mm/s2。由于单电池位移、速度和加速度频率响应曲线趋势基本相同，所以可直接以位移响应结果来分析单电池的动态特性。单电池进行谐响应分析得到了在X轴、Y轴和Z轴3 个方向上的位移响应，见图5。

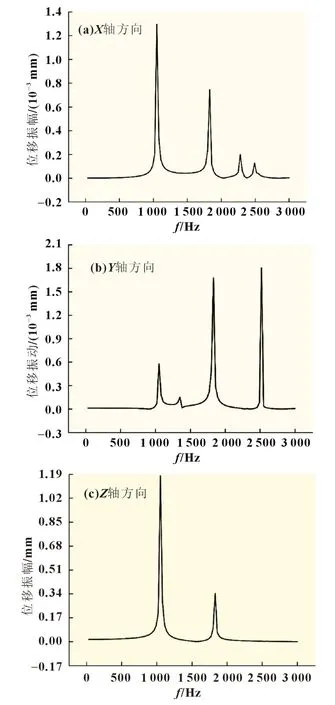
图5 单电池在X、Y、Z方向位移频率曲线

在X轴方向上，频率在1 050、1 830、2 280 和2 490 Hz 处出现峰值；在Y轴方向上，频率在1 050、1 830 和2 520 Hz 处出现峰值；在Z轴方向上，频率在1 050 和1 830 Hz 处出现峰值。根据以上数据发现，X轴方向和Z轴方向在频率1 050 Hz时位移振幅最大，分别为1.30×10-3和1.18 mm，Y轴方向在频率2 520 Hz 时位移振幅最大，为1.80×10-3mm，Z轴方向振幅最大，X轴方向振幅最小。原因是根据单电池在电池堆里的安装条件，对单电池四周进行了固定约束，使得结果分析中X轴和Y轴方向上的振幅要远远小于Z轴方向上的振幅。

3 个方向上的响应都在频率为1 050 和1 830 Hz 时出现峰值，且这两频率分别与模态的第1 阶和第3 阶固有频率十分接近，因此单电池对这两频率附近的振动最敏感，容易引起共振现象，为保证燃料电池本体的安全运行，应当避免在这两频率附近的振动环境下工作。

4 结语

建立了质子交换膜燃料电池单电池的三维模型，并将其导入有限元分析软件中建立了单电池的有限元模型。根据单电池在电池堆的实际安装情况，对单电池进行了模态分析和谐响应分析，计算得到了单电池的前6 阶固有频率和振型，以及正弦激励下的频率与振幅响应曲线。计算结果表明，单电池的薄弱部位位于气体出入口周围，在设计时需适当进行优化。单电池在1 050 和1 830 Hz 频率附近的激励下容易产生较大的振动，应尽可能避免在相近频率的环境下工作，以免出现共振现象给单电池带来较大的疲劳破坏。