机器人关节传动系统固有特性分析
2022-10-21胡效松杨振宁冯志友周长鹏黄云生
莫 帅 胡效松 杨振宁 冯志友 李 旭 周长鹏 黄云生
(1 天津工业大学 机械工程学院, 天津 300387)
(2 江苏万基传动科技有限公司, 江苏 泰州 225400)
(3 深圳市合发齿轮机械有限公司, 广东 深圳 518100)
0 引言
随着智能制造技术快速发展,机器人的种类以及应用场景也更加广泛,例如多功能机械臂、教育机器人、服务机器人等。机器人关节作为机器人的核心部件,主要由驱动控制部分和电机-齿轮传动系统构成。机器人关节所用电机多是无刷直流电机,具有转速高、转矩大等特点,在电机拖动齿轮传动系统转动时,齿轮传动系统的动力学特性变得十分复杂[1]。在长时间高转速、高负载下,可能会出现“扫齿”“断齿”等故障,有必要对机器人关节中齿轮传动系统固有特性进行分析。
目前,国内外学者对齿轮传动系统固有特性进行了大量研究。王均刚等[2]建立风电增速箱多级耦合传动系统动力学模型,研究了系统的固有频率和振动模式。Liu 等[3]建立风力发电机多级齿轮传动系统动力学模型,计算了该系统的固有频率和主振型。黄孝慈[4]建立混合动力汽车多级齿轮系统动力学模型,分析了阻尼、刚度等参数对系统产生的扭转振动的影响。Li等[5]对齿轮传动系统的故障状态进行模态分析,比较了不同故障形式对齿轮振动特性的影响。张丽娟[6]建立多级齿轮传动系统微分方程,求解了系统各部件的振动加速度。李楠等[7]建立功率四分支齿轮传动系统动力学模型,并对该系统的固有特性和动载系数变化进行了分析。Mo 等[8-9]建立齿轮行星系统动力学模型,对该系统的均载特性和固有频率进行了分析。李国彦等[10]以复合两级行星轮系为研究对象,分析了裂纹对该系统振动的影响。Lu等[11]建立两级行星齿轮和多级正齿轮传动系统的耦合模型,阐明了内外激励对复杂传动系统振动特性的影响。Shao 等[12]根据齿轮的实际工况,将支撑齿轮轴作为弹性支撑,研究了其对齿轮传动系统振动的影响。鲍和云等[13]利用集中质量法建立了直升机传动系统动力学模型。黄晓冬等[14]建立多级平行轴滚筒齿轮数学模型,分析了系统的动力学特性。王海霞等[15-16]建立船用齿轮箱传动系统耦合动力学方程,计算了在时变啮合刚度等条件下该系统的固有特性。胡鹏等[17]建立考虑时变刚度等因素的多级齿轮传动系统动力学模型,研究了系统运行的平稳状况。
以往对于小型、小模数齿轮传动系统的研究较少,而这类系统内部结构更加复杂。机器人关节体型小,内部构件连接更加紧密,电机驱动电路板、无刷电机和齿轮传动系统在结构上是整体结合在一起的,其动力学特性更是复杂多变。通过对机器人关节进行齿轮传动系统固有特性分析,可以了解该系统振动情况,为机器人齿轮传动系统设计提供理论依据。
图1所示为研究的机器人关节及其传动结构,主要由外壳、驱动电路板、电机、多级齿轮系统所构成。其中,齿轮传动系统为4级定轴齿轮机构。本文中针对机器人关节小模数齿轮传动系统建立动力学模型,进行了系统固有频率、模态能分析,研究了系统参数对固有频率的影响,分析了在刚度变化时,系统固有频率发生的模态跃迁现象。

图1 机器人关节及其传动结构Fig.1 Robot joint and its transmission structure
1 动力学模型
为对机器人关节齿轮传动系统进行研究,基于集中参数法建立了该系统动力学模型,如图2 所示。系统中齿轮的啮合、传动轴的支撑和扭转用具有一定刚度系数的弹簧表示,用K、C和e配上相应的下标分别表示刚度、阻尼和啮合误差。通过分析各齿轮的运动规律和自由度,得到系统的广义位移矩阵为
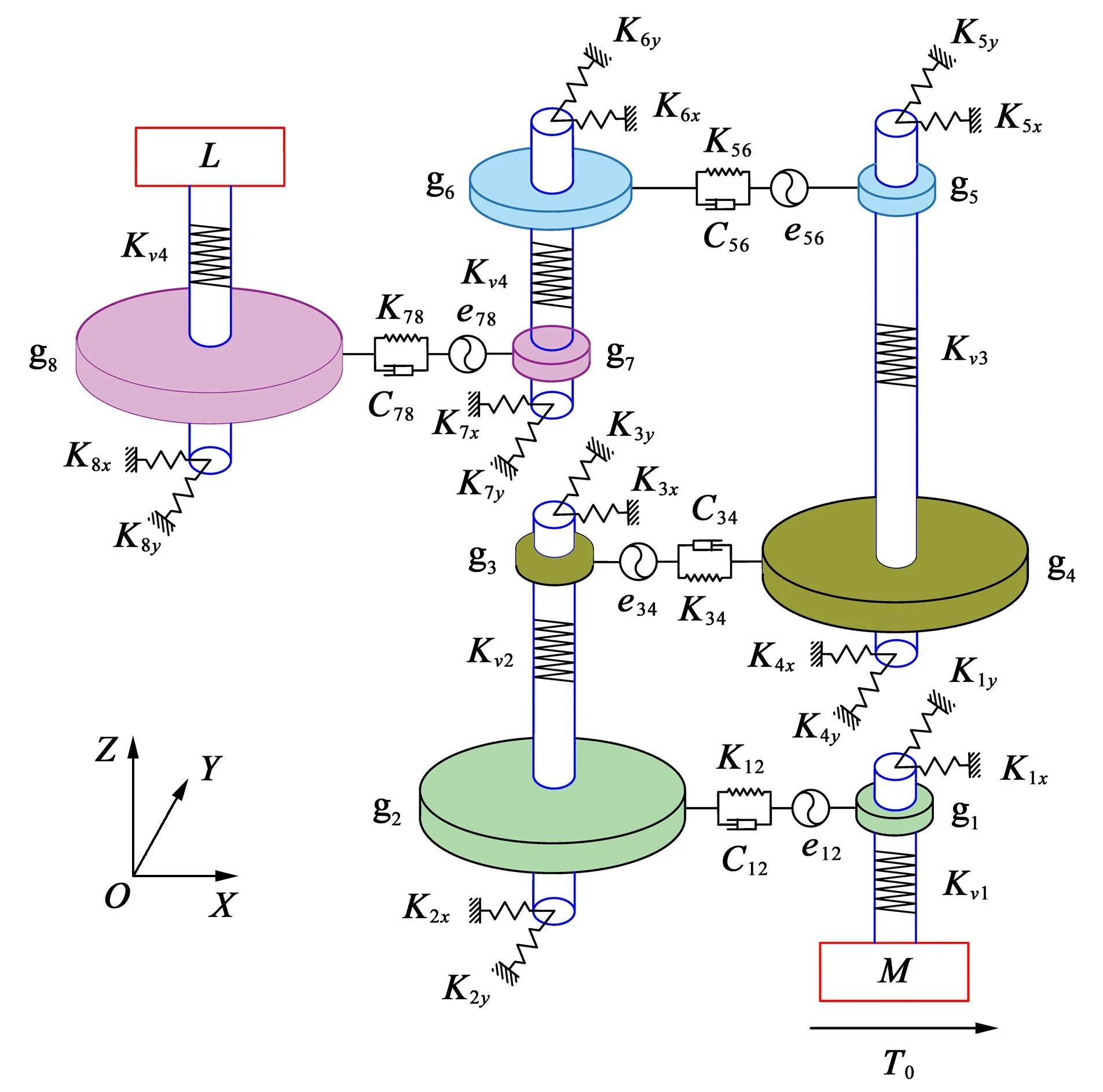
图2 机器人关节齿轮传动系统动力学模型Fig.2 Dynamic model of robot joint gear transmission system
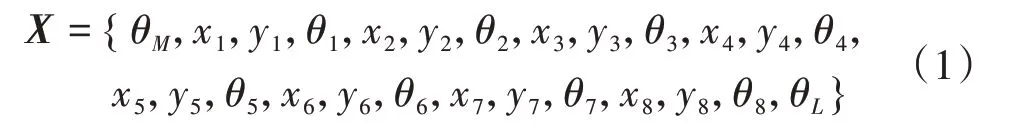
式中,x、y、θ分别为各构件沿坐标轴x、y的平移振动位移和绕中心轴的扭转振动角度。
2 齿轮传动系统动力学方程
2.1 啮合力与啮合阻尼力求解
图3 所示为齿轮副平移-扭转振动模型,显示了处于啮合状态齿轮副的受力情况和相对位置关系。根据啮合原理进行分析,在齿轮啮合过程中,齿轮副在啮合点处会因振动位移和误差产生微位移,在计算齿轮副的啮合力和啮合阻尼力时,需要将每个齿轮的微位移投影到啮合线上,以获得齿轮副相对位移。

图3 齿轮副平移-扭转振动模型Fig.3 Translational torsional vibration model of gear pair
在机器人关节齿轮传动系统中,各级齿轮副的相对位移δ分别为
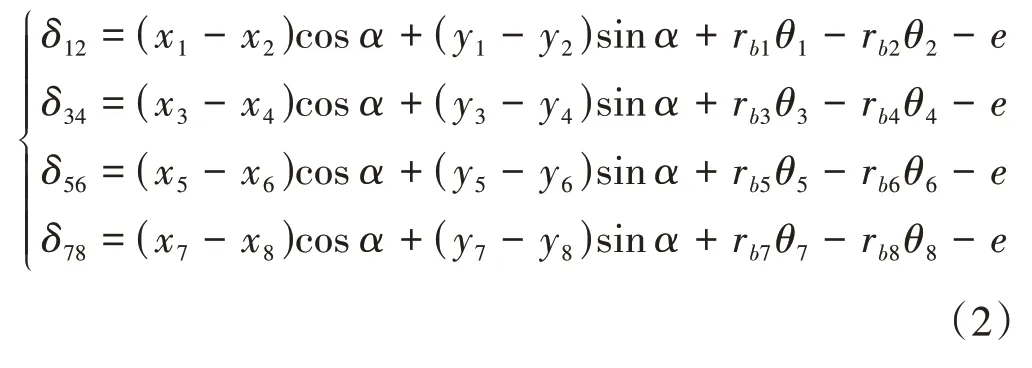
式中,rbi为齿轮i的基圆半径;α为两齿之间的压力角;θi为齿轮i(i=1,2,…,8)的转角;e为齿轮综合啮合误差。
各级齿轮副的啮合力和啮合阻尼力分别为
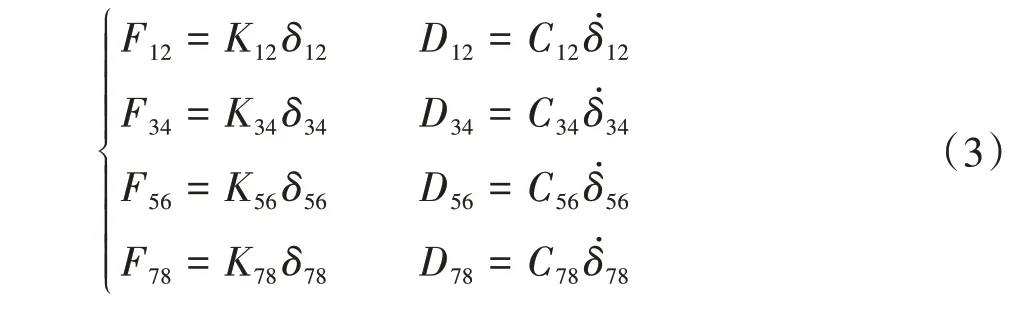
式中,F12、F34、F56、F78均为齿轮间的动态啮合力;D12、D34、D56、D78均 为 齿 轮间 的 啮合 阻尼 力;K12、K34、K56、K78均为齿轮啮合刚度;C12、C34、C56、C78均为齿轮啮合阻尼系数。
2.2 动力学微分方程
通过分析各构件的受力情况,根据牛顿第二定律建立各构件的运动微分方程。以下各式中,m表示质量,J表示转动惯量。
第一级齿轮副u12中主动轮g1和从动轮g2的动力学方程分别为
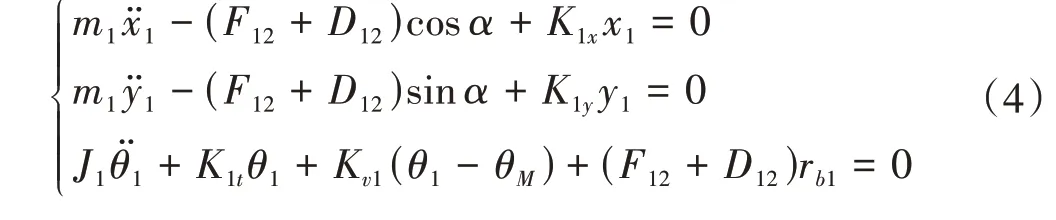
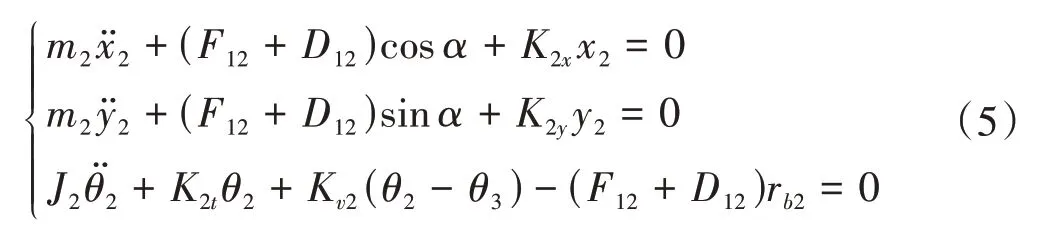
第二级齿轮副u34中主动轮g3和从动轮g4的动力学方程分别为
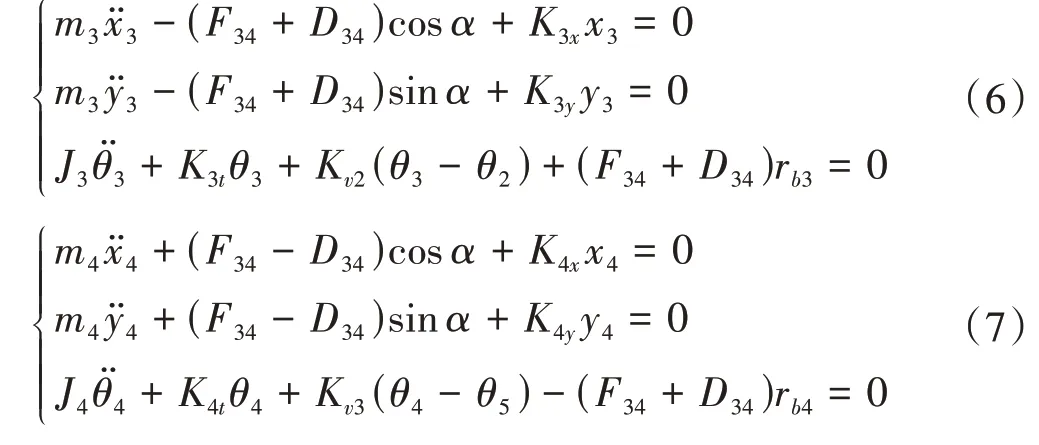
第三级齿轮副u56中主动轮g5和从动轮g6的动力学方程分别为
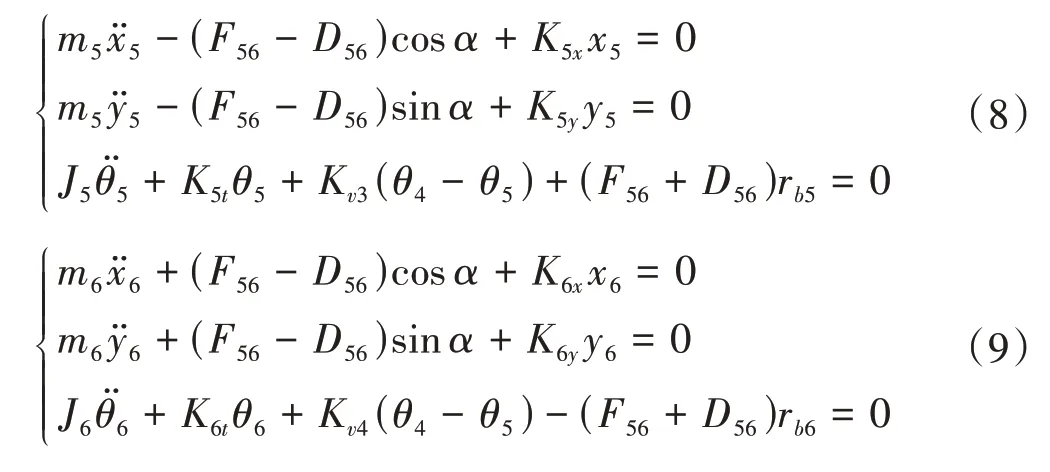
第四级齿轮副u78中主动轮g7和从动轮g8的动力学方程分别为
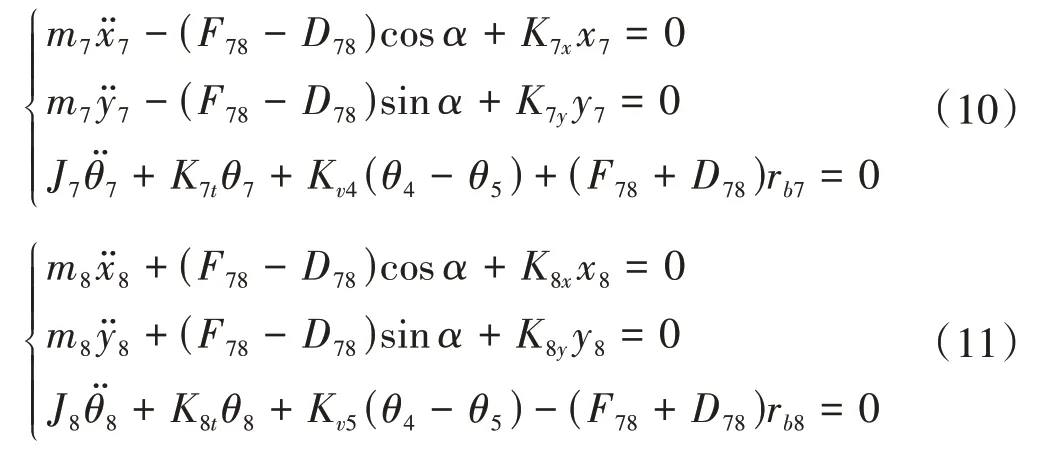
输入构件M和输出构件L的扭转振动方程为
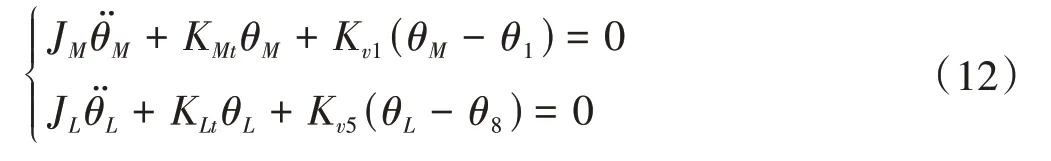
式中,Kix为齿轮i的x方向支撑刚度;Kiy为齿轮i的y方向支撑刚度;Kit为构件i(i=M,1,2,…,8,L)的切向支撑刚度;Kvj为传动轴j(1,5 为输出、输出轴;2、3、4分别为双联轴Ⅰ、Ⅱ、Ⅲ)的扭转刚度。
3 机器人关节齿轮传动系统固有特性分析
机器人关节齿轮传动系统采用4级定轴齿轮结构设计。其多级齿轮系统基本参数如表1所示。
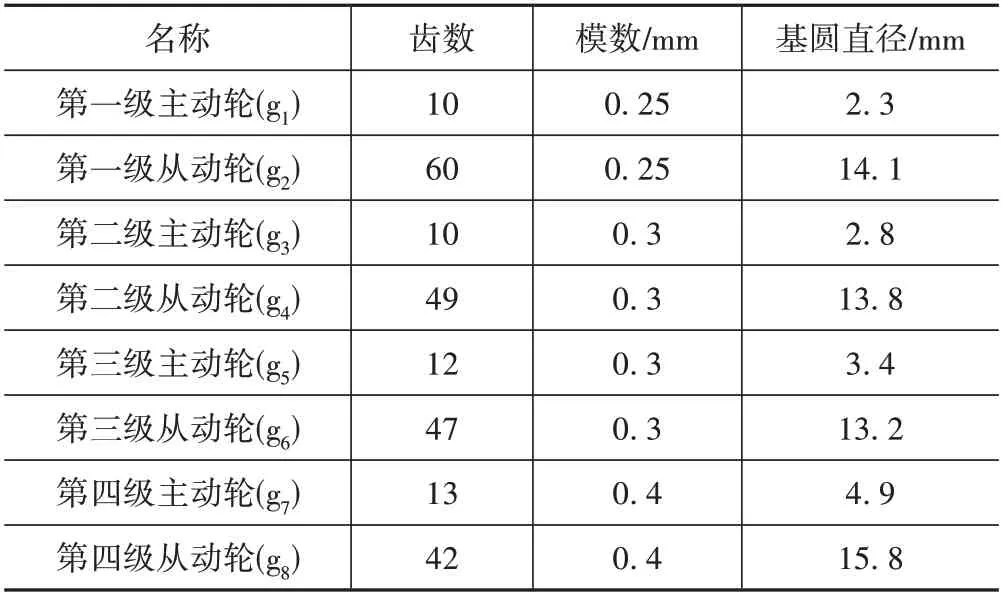
表1 多级齿轮系统基本参数Tab.1 Basic parameters of multi-stage gear system
3.1 固有频率求解
固有频率是系统固有特性的反映,只由系统本身决定。在忽略各弹性构件的阻尼以及内、外部激励后,利用建立的齿轮传动系统动力学方程,可得到系统无阻尼自由振动方程,其形式为

式中,M为质量矩阵;X为位移矩阵;K为刚度矩阵。

式中,wn为第n阶固有频率;φn为固有频率n(n=1,2,…,26)对应的振型矢量。
求解式(14),可以得到系统固有频率如表2所示。
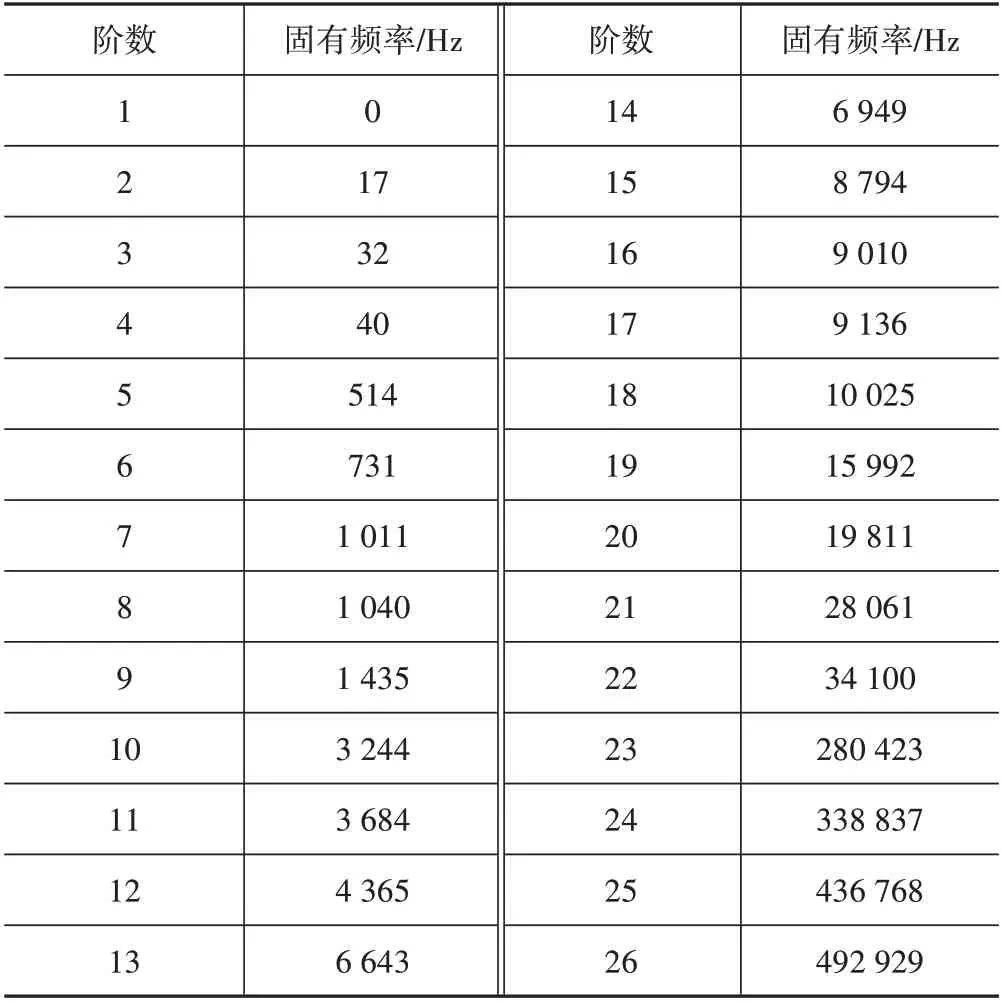
表2 系统固有频率Tab.2 System natural frequency
3.2 模态能分析
3.2.1 模态应变能分析
模态应变能可以表示齿轮的变形程度。通过对机器人关节齿轮传动系统进行啮合应变能和支撑应变能分析,可以得到系统各构件振动以及形变大小,对研究系统的稳定性与可靠性有重要意义。
齿轮副啮合应变能Uu为

式中,u表示4级齿轮副。
齿轮振动产生的支撑应变能Uf为

由式(16)可以得到整个系统的第n阶固有频率下的总应变能为
通过研究与示范,核心试验区内氮磷肥投入量降低20%,化肥利用率提高5个百分点;畜禽粪便减少排放60%以上。技术示范区内氮磷肥投入量降低10%,化肥利用率提高3个百分点,农业面源径流氮磷损失量减少30%。泥沙流失降低80%,径流损失降低40%,富营养化物质的流失量控制在临界值内;面源污染物截纳率,总氮为60%、总磷为70%。农业废弃物资源化回收率达到60%以上。

图4所示为系统中各阶固有频率下的齿轮副啮合应变能。可以看出,齿轮副u34在第24 阶固有频率下,齿轮副u56在第18阶、第21阶固有频率下,齿轮副u78在第15阶、第20阶固有频率下,均有较大啮合应变能出现;而齿轮副在其他阶数所产生的啮合应变能较小。

图4 啮合应变能Fig.4 Meshing strain energy
图5所示为系统中各阶固有频率下的齿轮支撑应变能。可以看出,齿轮g1在第25 阶、第26 阶固有频率下,齿轮g2在第7阶、第10阶固有频率下,齿轮g3在第22 阶固有频率下,齿轮g4在第24 阶固有频率下,齿轮g5在第18 阶固有频率下,齿轮g6在第8 阶、第11 阶固有频率下,齿轮g7在第15 阶固有频率下,齿轮g8在第3阶固有频率下,均有较大支撑应变能。
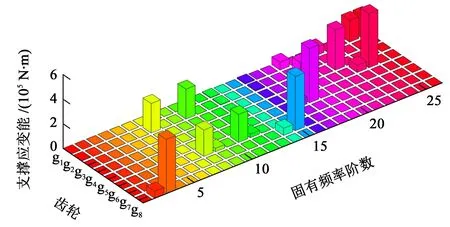
图5 支撑应变能Fig.5 Support strain energy
图6 所示为系统中各阶固有频率下的构件总应变能。总结可知,在系统正常运行过程中,第15 阶频率下的总应变能最大,此时齿轮传动系统整体变形最大。
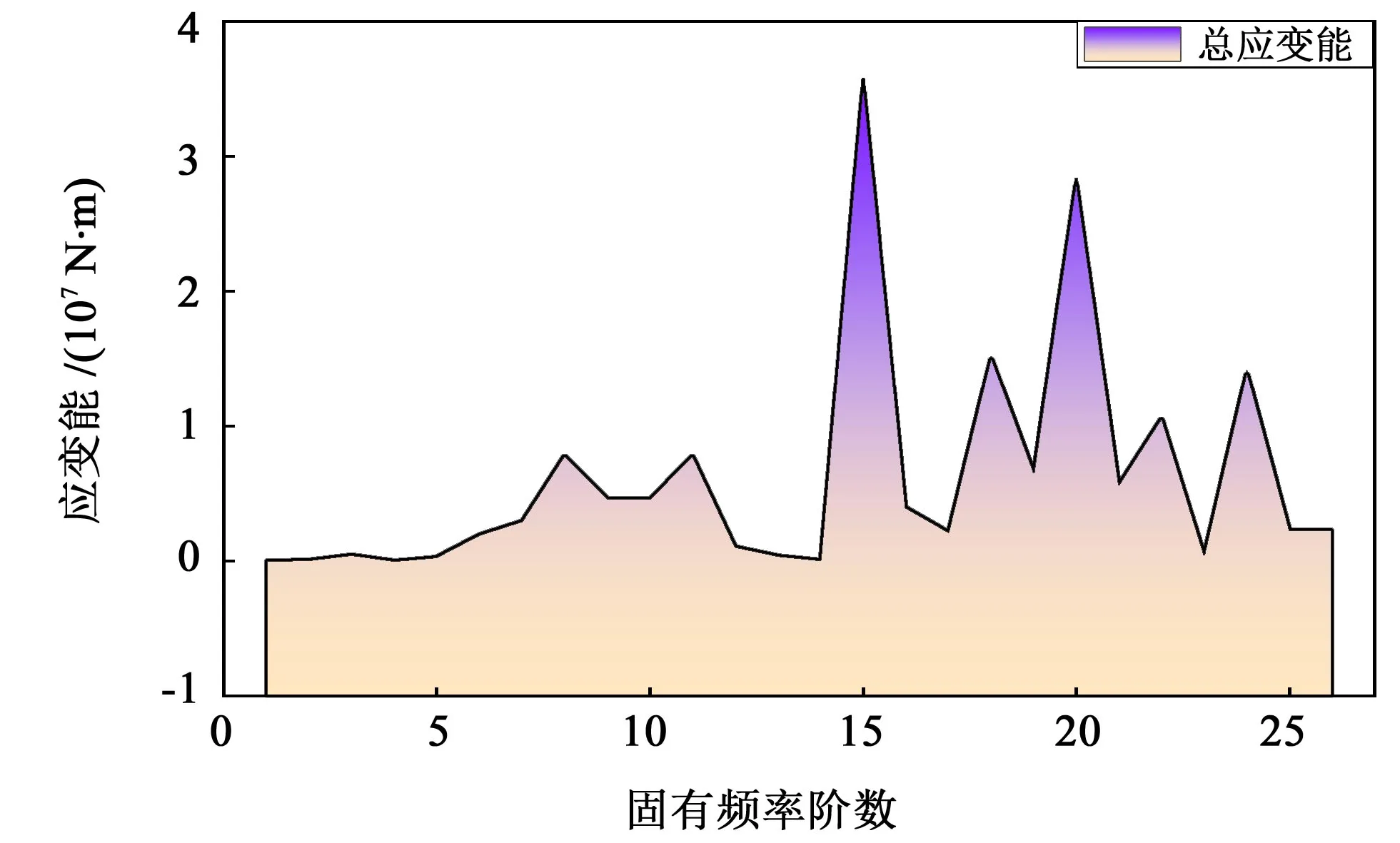
图6 系统总应变能Fig.6 Total strain energy of system
3.2.2 模态动能分析
模态动能可以表示齿轮振动的剧烈程度,由扭转动能和平移动能组成。
齿轮振动产生的扭转动能Eia为

式中,λi为特征值。
齿轮振动产生的平移动能Eib为


图7所示为齿轮传动系统扭转动能在各阶固有频率下的分布状态。可以明显看出,构件g3在第25阶、第26 阶固有频率下,构件g4在第12 阶固有频率下,有很大的扭转动能。
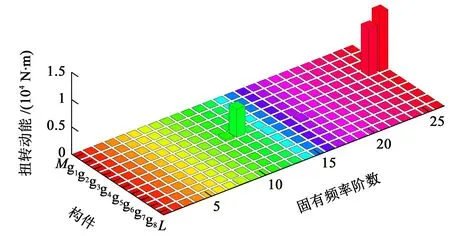
图7 扭转动能Fig.7 Torsional kinetic energy
图8所示为系统中各阶固有频率下构件的平移动能。可以看出,构件g4在第23 阶、第24 阶固有频率下有很大的平移动能。
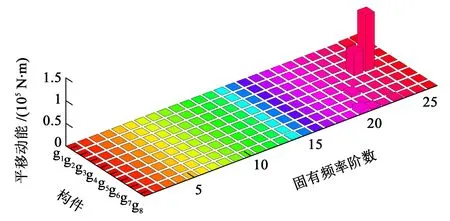
图8 平移动能Fig.8 Translational kinetic energy
总结可知,在该系统中,构件g3、构件g4有明显的应变能增大现象,应注重改善其振动情况。
图9所示为机器人关节齿轮传动系统中各阶固有频率下的构件总动能。可以看出,在第24 阶固有频率下的系统总动能最大,齿轮传动系统在该固有频率下的振动最为剧烈。
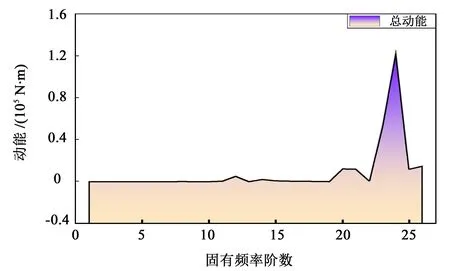
图9 系统总动能Fig.9 Total kinetic energy of the system
4 系统参数对传动系统固有频率的影响
分析机器人关节齿轮传动系统参数对固有频率的影响,可以了解系统振动的特性,为设计机器人关节、改善齿轮传动系统稳定性提供依据。系统的刚度和构件质量对系统固有频率影响较大。因此,通过改变啮合刚度、支撑刚度和构件质量,分析系统固有频率的变化。
4.1 啮合刚度对固有频率的影响
通过改变系统各级齿轮副之间的啮合刚度,保持系统中其他参数不变,观察系统固有频率的变化。图10 所示为四级齿轮啮合副固有频率随啮合刚度改变而产生的变化。
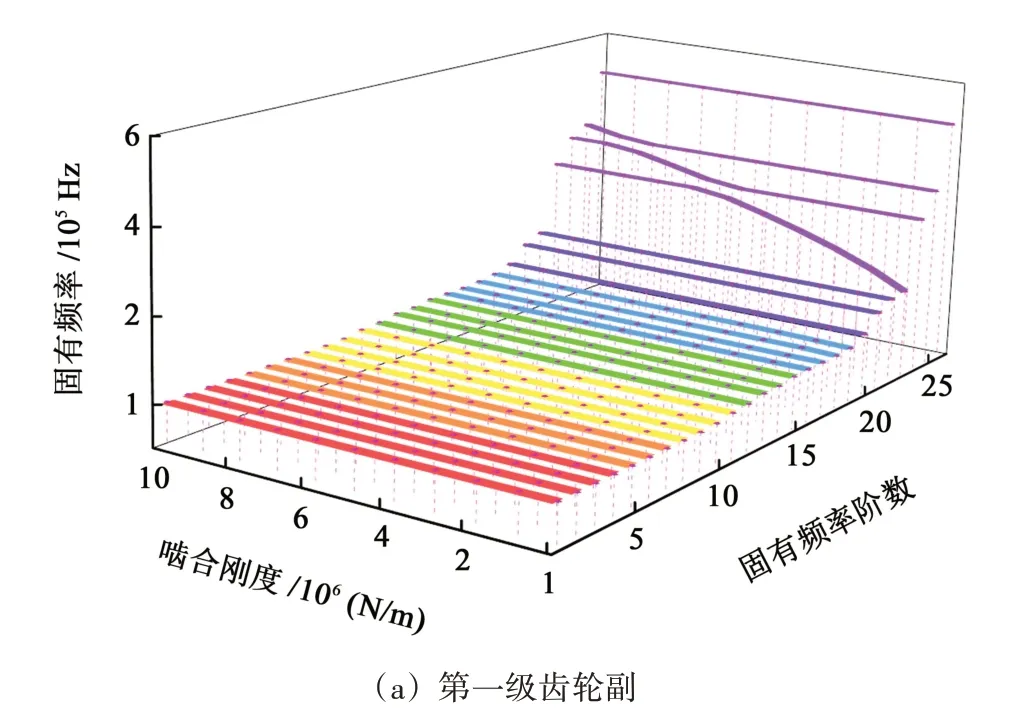
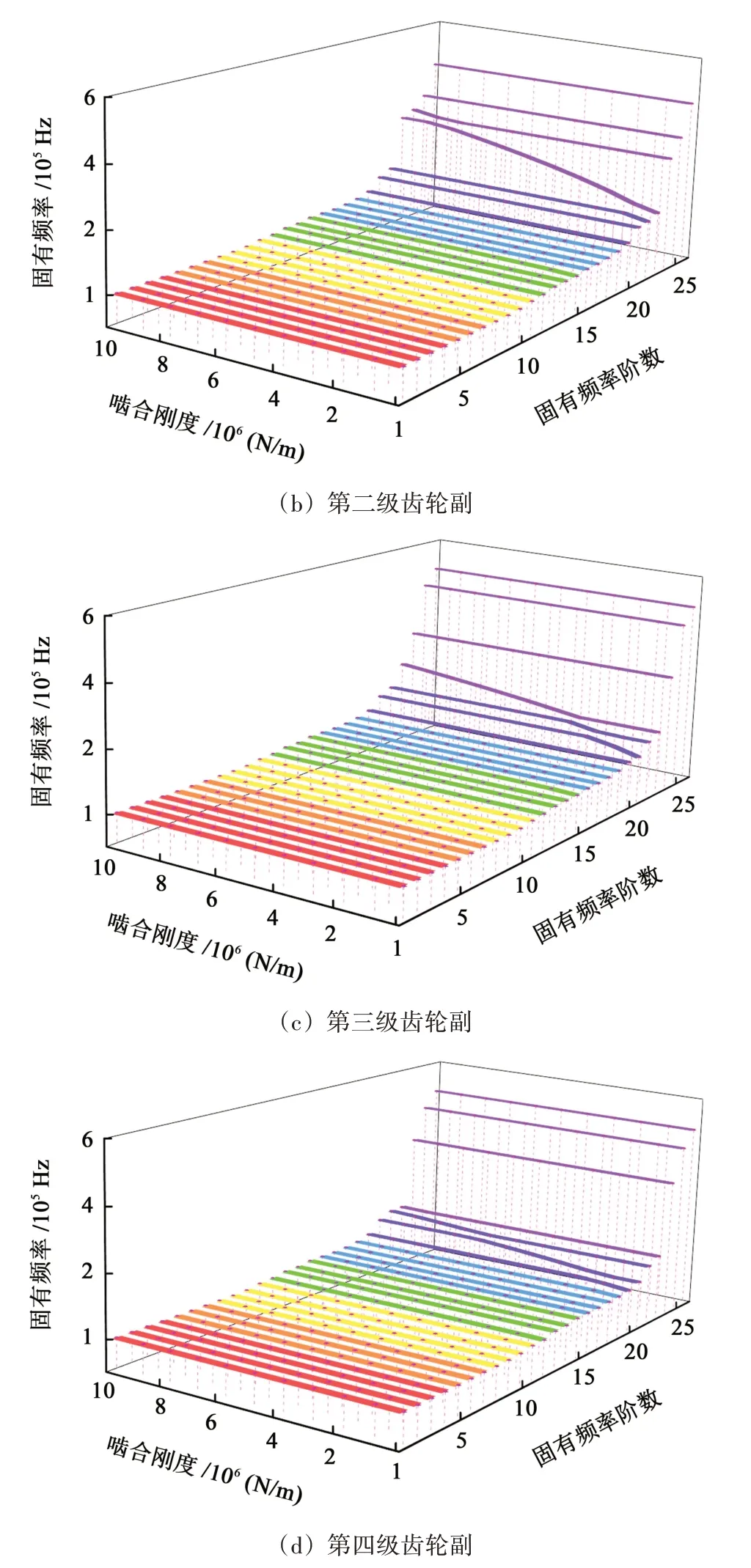
图10 齿轮副啮合刚度对固有频率的影响Fig.10 Influence of meshing stiffness of gear pair on natural frequency
从图10 中可以看出,在该系统中,第20 阶至第26 阶固有频率,受齿轮副啮合刚度变化影响明显,个别阶数下的固有频率会出现增大现象。如图10(a)中的第23 阶、第24 阶固有频率,图10(b)中的第23阶固有频率以及图10(c)中的第23 阶固有频率,都出现了明显的大幅度增大。
总结可知,在机器人关节齿轮传动系统中,随着齿轮副啮合刚度增大,高阶固有频率受啮合刚度变化影响较大,低阶固有频率受影响较小。
4.2 支撑刚度对固有频率的影响
通过改变系统传动轴支撑刚度,设置支撑刚度从1×106N/m 增加到1×107N/m,保持系统中其他参数不变,观察系统固有频率的变化。
图11所示为传动轴支撑刚度对固有频率的影响。可以看出,在传动轴支撑刚度变化时,高阶固有频率受影响较大,低价固有频率受影响较小。其中,前两个传动轴固有频率受支撑刚度影响较为明显。由图11(a)中可以看出,随着输入轴支撑刚度增加,第22 阶和第23 阶~第26 阶固有频率都会增大,其余阶数固有频率受影响较小。由图11(b)中可以看出,随着双联轴Ⅰ支撑刚度增加,第22 阶和第25 阶固有频率增幅较为明显;其余阶次的固有频率受影响较小。
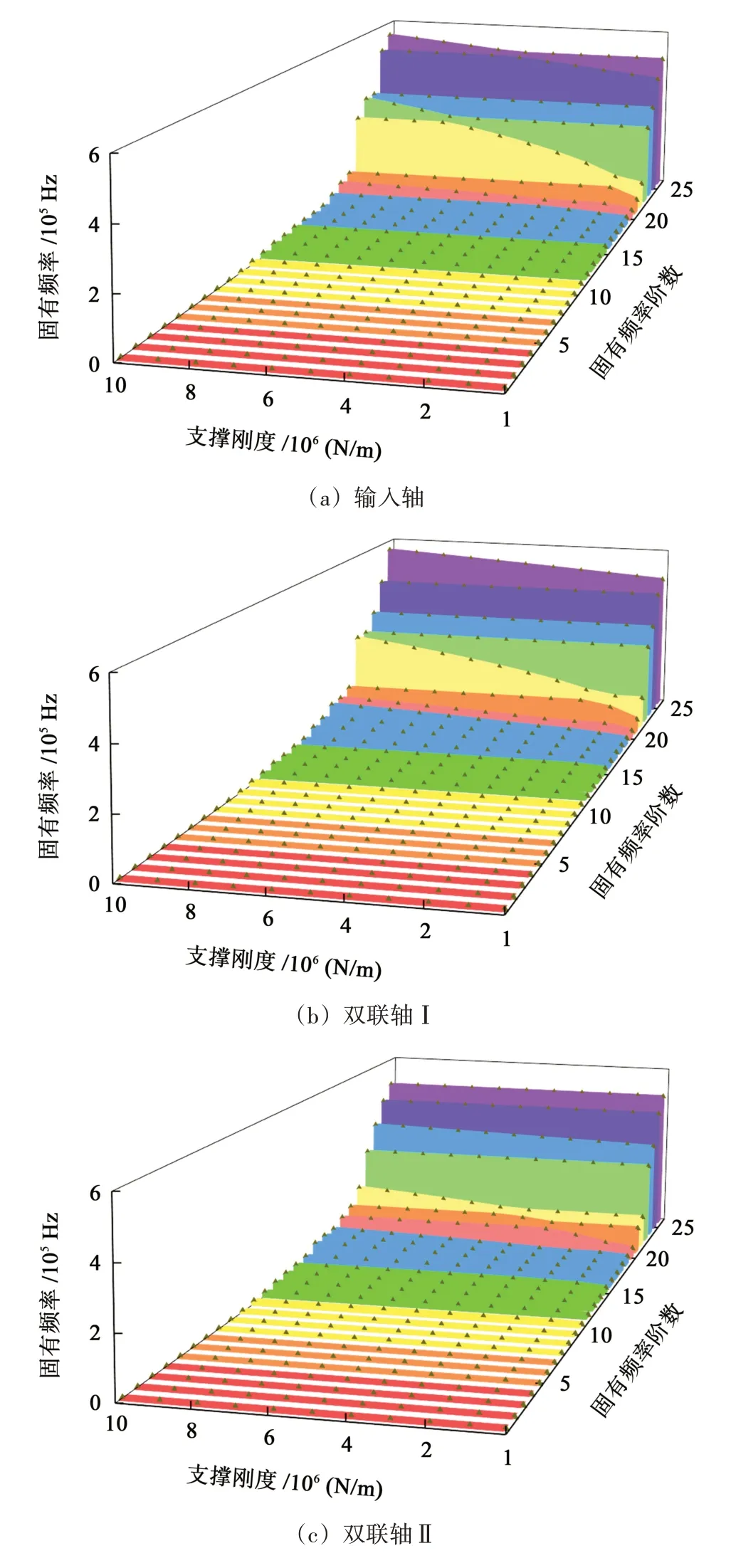
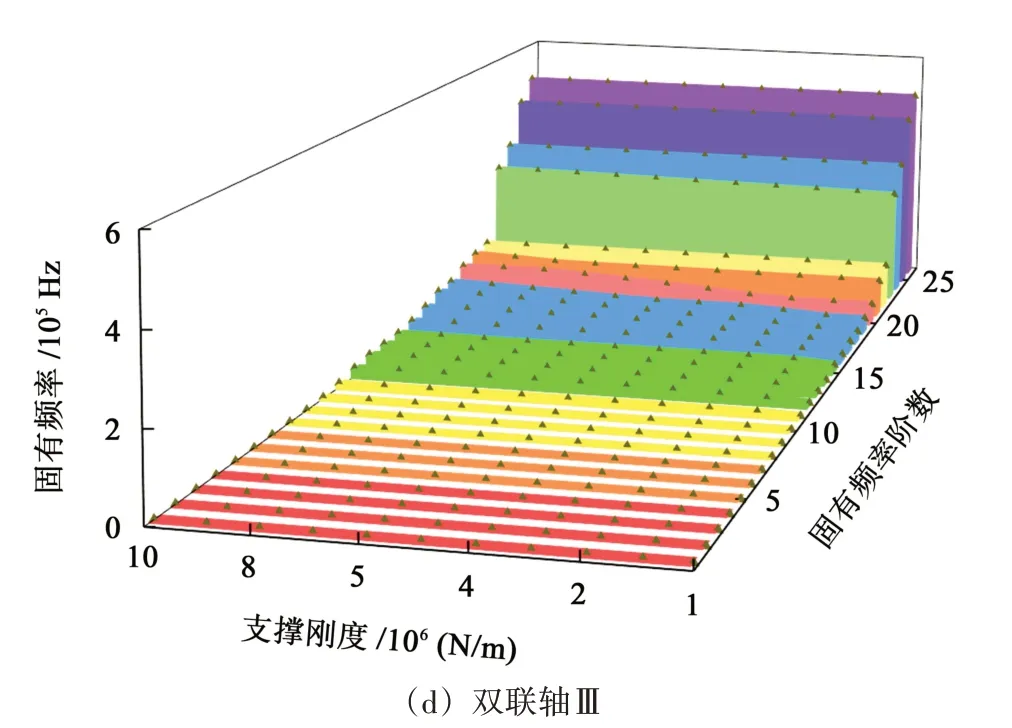
图11 传动轴支撑刚度对固有频率的影响Fig.11 Influence of transmission shaft support stiffness on natural frequency
总结以上规律可知,在机器人关节齿轮传动系统中,高速级齿轮传动轴相较于低速级振动情况更为剧烈。
4.3 质量对固有频率的影响
机器人关节齿轮传动系统中构件的质量对系统固有频率影响较大。图12所示为齿轮g1、齿轮g2、齿轮g3和齿轮g4质量增大时,系统固有频率的变化规律。
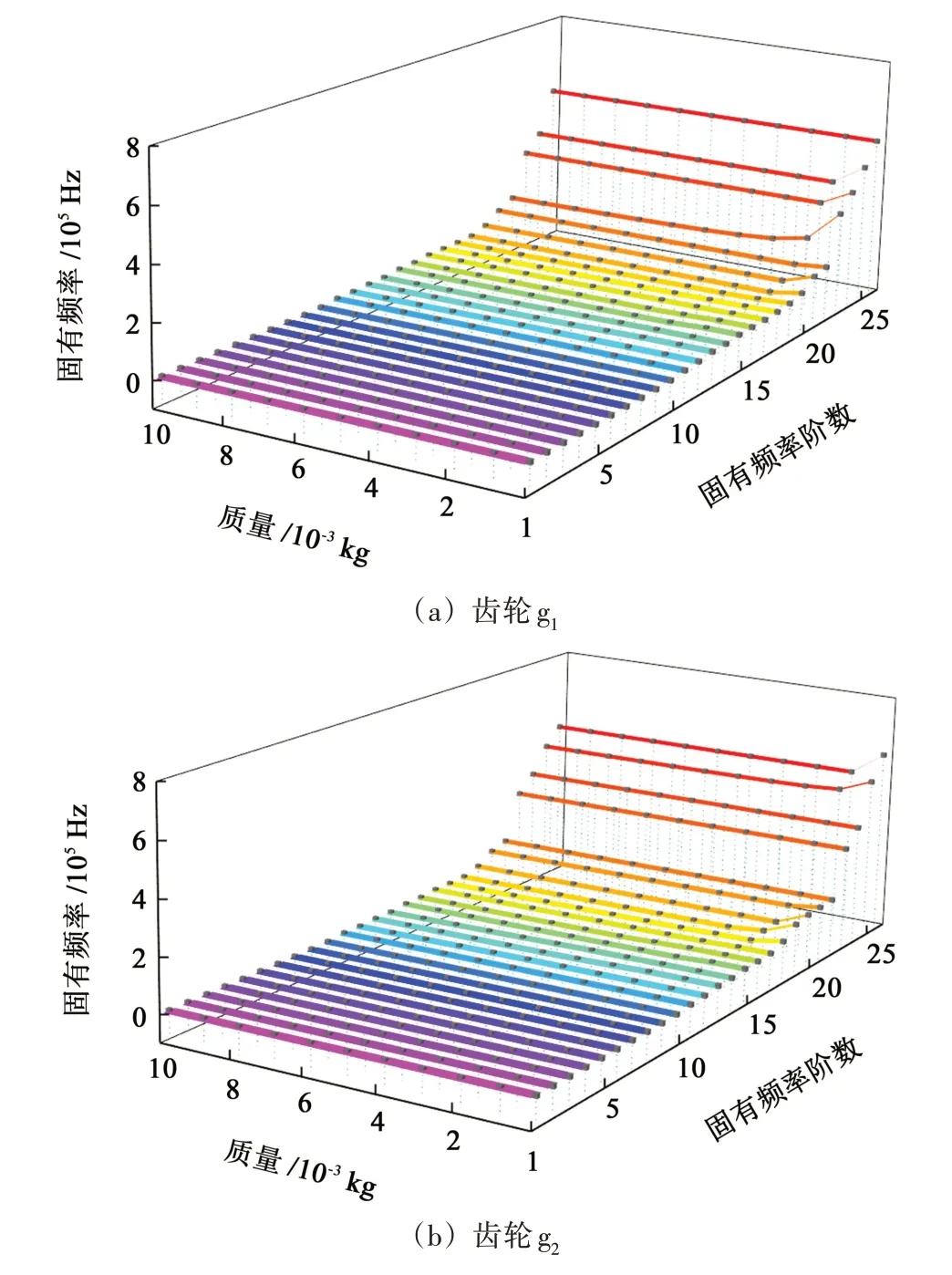
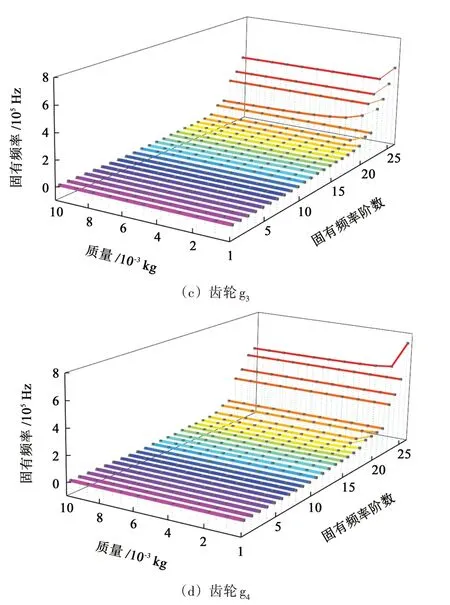
图12 齿轮质量对固有频率的影响Fig.12 Influence of gear mass on natural frequency
可以看出,随着系统中齿轮质量增大,齿轮g1在第20 阶~第25 阶固有频率,齿轮g2在第18 阶、第19阶、第20 阶、第21 阶、第25 阶和第26 阶固有频率,齿轮g3在第20 阶、第21 阶和第23 阶~第26 阶固有频率,齿轮g4在第18阶~第19阶和第26阶固有频率,均会出现前期迅速减小,减小到一定程度后基本不变的现象。
由图12 中总结可知,构件质量对系统高阶固有频率影响较大,对低价固有频率影响较小,而且部分高级固有频率随着构件质量增加,前期会迅速减小到一定程度,后面基本不再变化。
4.4 模态跃迁现象
从系统固有频率随刚度增加得到的变化规律曲线,可以看到模态跃迁现象。模态跃迁是指随着系统参数的变化,固有频率轨迹曲线会先慢慢接近,然后在某点附近又以比较大的曲率快速分离的一种现象[18]。
对于机器人关节齿轮传动系统,随着系统参数刚度的增加,低价固有频率受影响较小,高价固有频率受影响较大。因此,通过分析系统第21 阶~第26 阶固有频率随着齿轮副啮合刚度和传动轴支撑刚度增加,观察系统固有频率轨迹曲线变化,分析模态跃迁现象。
如图13(a)所示,系统固有频率随着第一级齿轮副啮合刚度不断增大,第23 阶、第24 阶固有频率曲线在点A1、点B1附近,第24 阶、第25 阶固有频率曲线在点C1、点D1附近都是渐渐接近,然后以比较大的曲率快速分离,这均为模态跃迁。
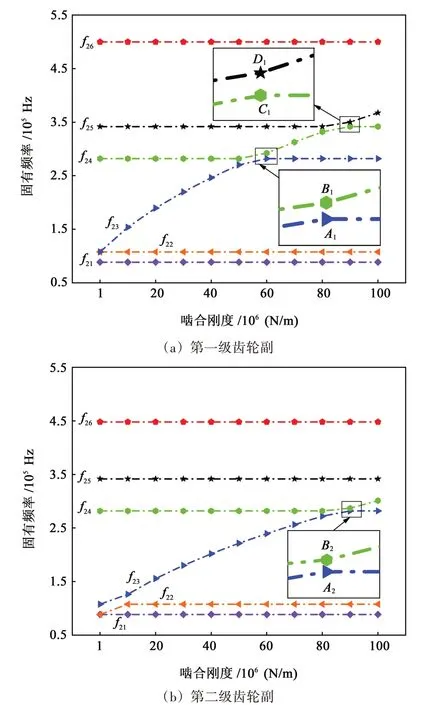
图13 系统固有频率随啮合刚度的变化规律Fig.13 Variation law of natural frequency of system with meshing stiffness
如图13(b)所示,系统固有频率随着第二级齿轮副啮合刚度不断增大,第23 阶、第24 阶固有频率曲线在点A2、点B2附近逐渐靠近后又以不同的曲率分离,发生了模态跃迁现象。
在图14(a)中,系统固有频率随着输入轴支撑刚度不断增大,第21 阶、第22 阶固有频率曲线在点A3、点B3附近逐渐靠近后,又迅速发生分离,这是出现了模态跃迁现象;第22 阶固有频率在点C3、点D3附近和第23 阶固有频率曲线渐渐接近,随后又快速分离,这是再次发生了模态跃迁现象;而第25阶、第26 阶固有频率曲线在点E3、点F3附近逐渐靠近后以不同的曲率分离,发生了模态跃迁现象。
在图14(b)中,系统固有频率随着双联轴Ⅰ支撑刚度不断增大,第21阶、第22阶固有频率曲线在点A4、点B4附近逐渐接近后迅速分开,发生了模态跃迁现象。
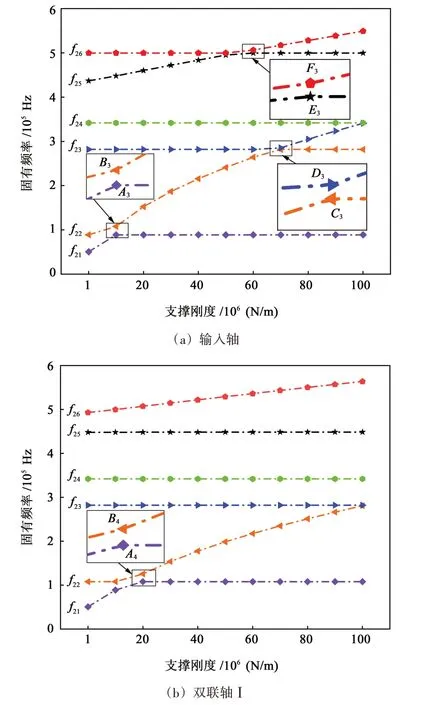
图14 系统固有频率随支撑刚度的变化规律Fig.14 Variation law of natural frequency of system with support stiffness
通过对系统刚度变化过程中振动模式的对比分析,发现出现模态跃迁现象时两组固有频率对应的模态振型会发生交换,之后维持不变,遇到频率接近欲相交的情况,再次跃迁。在进行机器人关节齿轮传动系统动态设计及传动特性的研究中,应该注意模态跃迁对其传动性能的影响。
5 结论
为研究机器人关节齿轮传动系统,文中首先采用集中参数法建立了动力学模型和运动微分方程,对系统的固有频率、模态能以及系统参数对固有频率的影响进行了分析。结论如下:
(1)针对系统模态能进行分析,可以看出在系统正常运行时,第15阶固有频率下的总应变能最大,此时齿轮传动系统整体变形最大;在第24 阶固有频率下系统总动能最大,齿轮传动系统在该固有频率下的振动最为剧烈。
(2)通过改变系统的刚度和质量等参数,可以看出系统高阶固有频率受到影响较大,低阶固有频率受影响较小。支撑刚度对固有频率的影响主要集中在系统高速级齿轮传动轴上;质量对固有频率的影响表现出,系统固有频率在前期会迅速减小,到一定程度后不再变化。
(3)系统的刚度变化会使系统出现模态跃迁现象,并且在出现模态跃迁现象时两组固有频率对应的模态振型会发生交换,之后维持不变,遇到频率接近欲相交的情况,会再次跃迁。
