源于直觉 启于思维 成于极限——以“圆柱、圆锥、圆台、球的表面积和体积”为例

翟洪亮

(太湖高级中学，江苏 无锡 214125)

1 问题提出

自2021年起江苏省高考采用全国卷，在教材使用上，苏州市和无锡市从2021年秋开始率先选用人教A版普通高中《数学》(以下简称人教A版新教材)．人教A版新教材与苏教版新教材在立体几何初步的编排上存在明显差异，苏教版新教材和原教材相比基本没变，人教A版新教材分为两大单元：一是空间几何体单元；二是位置关系单元．空间几何体单元包含简单几何体的表面积与体积，并按几何体的形状分为：棱柱、棱锥、棱台的表面积和体积；圆柱、圆锥、圆台、球的表面积和体积．位置关系单元包含空间点、线、面之间的位置关系；空间直线、平面的平行；空间直线、平面的垂直[1]．这样编排打破了原来以线线关系、线面关系、面面关系等空间集合间的关系作为分类标准，重新以平行和垂直划分作为两大体系．

这种标新立异的编排，有合理的一面，如位置关系分为平行与垂直两大体系就显得相对集中；也存在值得商榷之处，如对简单几何体的表面积与体积重新组合，在没有学习垂直的前提下进行体积教学，只能通过标注的形式给出棱台的高.特别是在圆柱、圆锥、圆台、球的表面积和体积中，一是直接给出圆柱、圆锥、圆台的表面积公式，显得有些杂乱，不能较好地体现它们侧面积间的内在联系；二是直接给出球的表面积公式，再推出球的体积公式，显得有些突兀．笔者在圆柱、圆锥、圆台、球的表面积和体积的教学中对教材进行简单整合，凸显极限思想的运用.现将教学过程整理如下，请同行批评指正．

2 教学设计

2.1 更新视角，凸显极限思想本质

师：前面我们学习了棱柱、棱锥、棱台的表面积和体积，今天我们一起学习圆柱、圆锥、圆台、球的表面积和体积.首先请大家思考：

问题1半径为r、母线长为l的圆柱的侧面积公式是什么？

沿着圆柱的任一母线将其侧面展开，可得长为圆柱底面周长、宽为母线长的一个矩形，故半径为r、母线长为l的圆柱的侧面积公式是S圆柱侧=2πrl．

问题2半径为r、弧长为l的扇形面积公式是什么？你是如何记忆的？

师：你是怎么想到的？

生1：由公式的形式想到的，特别是当扇形弧长很短时，当作等腰三角形就更直观了.

图1

师：这就是数学的直觉！如图1，我们把扇形AOB分成n份，当n越大时，每一份所对应的圆弧可近似地视为线段，每一个小扇形可以近似地看成一个以半径为腰、弧长为底的等腰三角形，它们的高都为半径r，于是可得扇形的面积

通过极限分割的方法达到化曲为直的目的,故可把扇形直观地视为“等腰三角形”来记忆它的面积．

问题3底面半径为r、母线长为l的圆锥的侧面积公式是什么？

如图2，圆锥的侧面展开图是半径为l、弧长为2πr的扇形，故

图2 图3

2.2 运用视角，理解记忆圆台公式

问题4下底面半径为r、上底面半径为r′、母线长为l的圆台的侧面积公式是什么？

如图3，设小圆锥的母线长为x，则

从而圆台的侧面积为两个圆锥侧面积之差，即

由相似三角形知识可得

即

从而

(c-c′)x=c′l，

问题5如何记忆和理解圆台的侧面积公式？

既然可以把扇形视为“等腰三角形”来记忆它的面积公式，那么圆台的侧面展开图就可视为由大的“等腰三角形”截去一个小的“等腰三角形”所形成的“等腰梯形”，因此可以用梯形的面积公式来记忆圆台的侧面积公式，其中“梯形”的上底边长为圆台的上底面周长c′，下底边长为圆台的下底面周长c，高为圆台的母线长l，即

设计意图从扇形面积公式出发，联想到三角形的面积公式，通过极限分割化曲为直，从而直观地理解把扇形抽象为“等腰三角形”的可行性根源所在，快速理解和推导圆台的侧面积公式．

2.3 利用极限，构建面积公式体系

问题6圆柱、圆锥、圆台的侧面积之间有什么关系？你能用圆柱、圆锥、圆台的结构特征来解释这种关系吗？

根据运动变化的观点，与记忆棱柱、棱锥、棱台的体积公式一样，也从中间状态——圆台出发，扩大圆台的上底面，圆台可以变成圆柱；将圆台的上底面缩小成一个点，圆台可以变成圆锥．故将圆柱、圆锥、圆台的侧面积分别加上它们的底面积可得它们的表面积．

设计意图类比棱柱、棱锥、棱台的体积公式，从中间状态——圆台出发，构建旋转体的侧面积之间的公式体系．

2.4 借助棱台，构建体积公式体系

问题8圆柱、圆锥、圆台的体积之间有什么关系？你能用圆柱、圆锥、圆台的结构特征来解释这种关系吗？

根据运动变化的观点，同样可得

特别地，对于正n棱柱、正n棱锥、正n棱台，当n越大时，

设计意图从棱台的体积公式出发，可联想到特殊的正棱台的体积公式，再利用极限思想从正n棱台的体积公式巧妙过渡到圆台的体积公式，结合运动变化的观点，再次认识圆柱、圆锥的体积公式之间的联系，结合棱柱、棱锥、棱台的体积公式，得到柱、锥、台的体积公式间的内在联系，加深对祖暅原理的理解和认识．

2.5 实验建模，推导球的体积公式

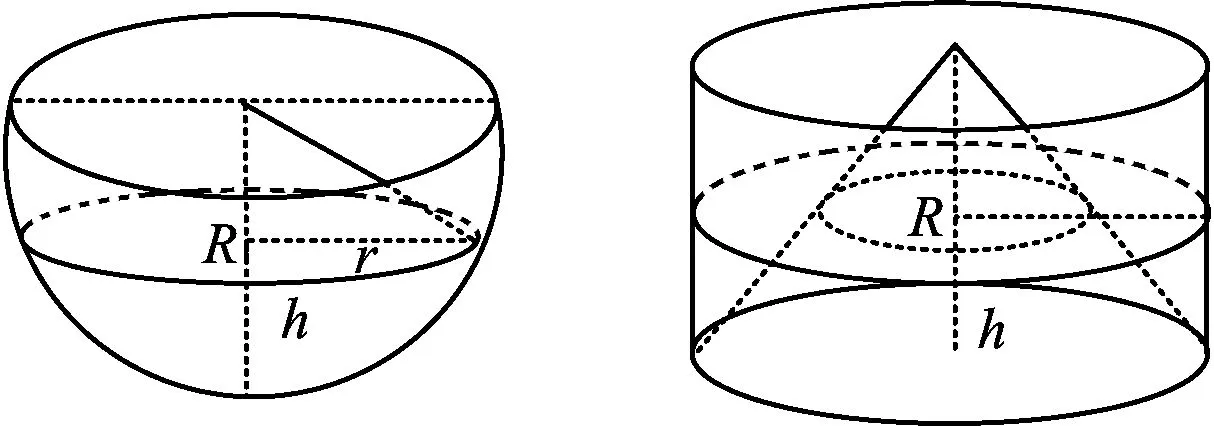
图4

由上述实验可知，半球的体积恰为圆柱的体积与圆锥的体积之差，从而引导学生根据祖暅原理设计推导球的体积公式的数学模型．如图4所示，根据半球的放置方式，若用平行于半球底面的平面去截半球，则上端是半径为R的圆面，下端是半球的顶点，从而让学生自然想到将圆锥放入圆柱内，用胶水将圆锥的底与圆柱的底面粘得密闭后，向半球和该模型内注入水.若二者的水深度都为h时，则半球中水面的面积为

S=π[R2-(R-h)2]，

模型内圆环中水面的面积也为

S=π[R2-(R-h)2].

根据祖暅原理可知

从而

把球的表面分割成n个小网格,面积分别记为S1，S2，…，Sn，它们与球心构成n个“小锥体”，当n越大时，每个“小锥体”的底面就越平，从而每个“小锥体”的高均为R，故

则

S球=4πR2．

设计意图在小学阶段,由圆柱的体积公式推导圆锥的体积公式是通过实验进行的，故本节课从实验出发，更贴近学生实际，引导学生构建数学模型，利用祖暅原理推导球的体积公式，再通过极限分割的思想方法推导球的表面积公式，显得较为自然．

2.6 讲解例题，体现新知应用价值

图5

问题10某种浮标由两个半球和一个圆柱黏合而成，半球的直径是0.3 m，圆柱高0.6 m.如果在浮标表面涂一层防水漆，每平方米需要0.5 kg涂料，那么给1 000个这样的浮标涂防水漆需要多少涂料(π取3.14)?

问题11如图5，圆柱的底面直径和高都等于球的直径，求球与圆柱的体积之比．

设计意图继续强化所学公式，解决实际问题，体现新知的应用价值，增强学生的应用意识．

3 课后思考

3.1 数学教学要注重自己的理解

数学教材为“教”与“学”提供了学习主题、基本线索和具体内容[2].任何版本的新教材都很难做到完美无缺，还需在使用过程中广泛听取使用者的意见和修改建议，反复修订才能日趋完善，因此数学教学是“用教材教”而不是“教教材”，这需要数学教师根据教学内容，结合学生的特点和自身理解，对教学内容进行一定的整合，创造性地开展教学．在本节课中，尽管教材直接给出了表面积公式，这“淹没”了圆柱、圆锥、圆台侧面积之间的内在联系，需要教师以运动变化的观点重新去“发掘”；对于圆台侧面积公式的理解与记忆，需要教师“点破”能以梯形面积公式加以理解和记忆的原因所在．所有这些只能建立在教师自己理解的基础之上，彰显个人的教学特色[3]．

3.2 数学教学要突出思想的渗透

数学教学不仅传授知识内容，还要以知识内容为载体进行数学思想方法的渗透．在本节课教学中除了进行数形结合数学思想的渗透外，还要注重数学极限思想方法的渗透.为了便于学生理解和记忆扇形面积公式，通过极限分割的方法寻找可以视“小扇形”为“等腰三角形”的合理性根源所在，从而用三角形的面积公式来记忆扇形的面积公式，在此基础上，将“扇环”视为“等腰梯形”，快速理解和记忆圆台的侧面积公式，并通过运动变化的观点，构建圆台与圆柱、圆台与圆锥的侧面积之间的联系．为了不直接给出球的表面积公式，在实验的基础上，通过祖暅原理推导球的体积公式，再用极限分割的方法推导球的表面积公式，这样设计使教学内容显得自然，学生在不知不觉中接受数学思想方法的熏陶．

3.3 数学教学要实现素养的提升

发展学生的数学学科核心素养是新一轮课程改革的主要任务，教学设计要把提升学生的数学核心素养渗透到教学的各个环节[4]．在新知的探究过程中，可发展学生的数学抽象和数学建模能力；在构建新知体系的过程中，可提升学生的数学推理和数学想象能力；在新知的运用过程中，可培养学生的数学运算和数据分析能力．如本节课中，源于直观可将扇形抽象成“等腰三角形”模型是本课的出发点，将运动变化观点贯穿于整个教学之中，通过问题串的形式，启迪学生进行思考，激发学生对新知的探索，加强师生间数学思想的交流，以达到“春风化雨，润物无声”的效果．