让逻辑推理核心素养落地——以疫情下一节线上复习课为例

周建峰

(浙江师范大学附属中学,浙江 金华 321004)

数学核心素养的培育已经成为当前数学教育的共识，从数学基础教育到高等教育都在不断探索数学核心素养生根落地的有效途径.其中，也不乏一些片面理解，如“在新课教学中培养核心素养，在复习课中抓应试能力”.其实，数学核心素养的培养是一个综合系统，新课中要重视核心素养的培养，复习课、专题课也是核心素养培育的重要阵地.

笔者有幸在2020年初新冠疫情暴发阶段，参加了浙江师范大学组织的“高考云众对”节目，利用网络直播的形式，以“数列”二轮复习为例，与广大师生聊聊高考那些事，其中的每个环节都精心设计并渗透了数学逻辑推理核心素养.

1 直播课片段

师：今天，老师将和大家一起以“数列”二轮复习为例，聊聊考题的素材和命题视角的变化，从中寻找不变的数学知识和思想方法，探寻知识的“根”与“芽”、命题的“源”与“流”.

环节1知识画像——逻辑推理的逻辑直观性.

1)学生活动：用知识框图的形式画出“数列”一章的“知识画像”，上传至指定QQ群(3分钟).

2)团队收集整理：从中选择3～5份，展现不同层次的学生的知识储备.

3)教师活动：通过3个层次的“知识画像”，分析学生的不同呈现形式(粗犷型、简约型、完美型)，最后呈现团队的作品(如图1).

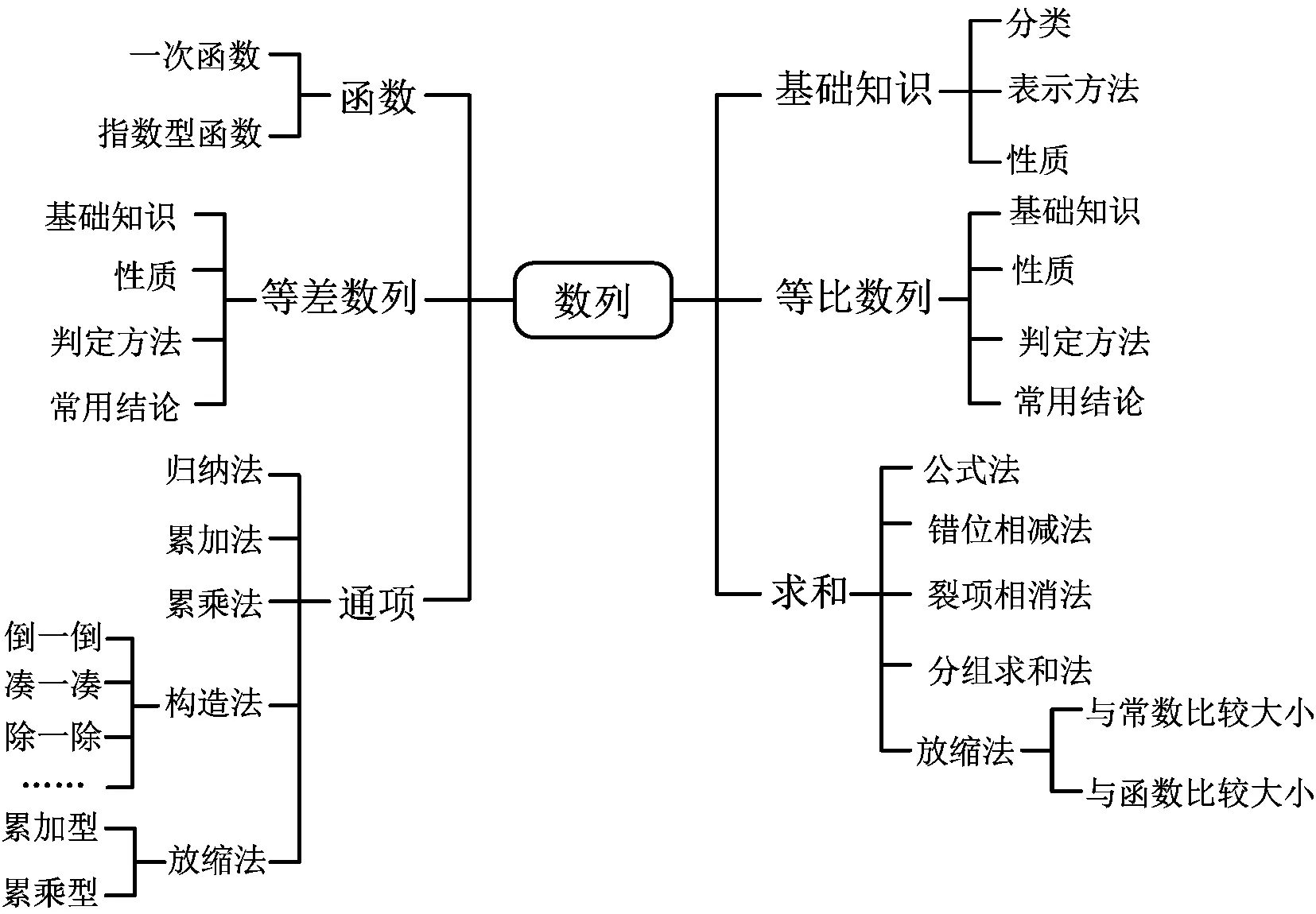
图1

评注逻辑推理核心素养既包含知识和方法的生成过程，也包括数学知识和方法的内在逻辑结构.在这一环节中，用知识框图的形式展示每位学生已有的知识储备，厘清知识的内在结构，直观体现了知识逻辑关系，这是逻辑推理核心素养的基础.

环节2结构生长——逻辑推理的思维发散性.

本环节采用师生云端同步合作的方法开展，学生可以随时将自己设计的结构关系发至指定QQ群与教师互动.

1)形式变化：从原始结构(即a1=1，an+1-an=1)出发，通过合理构造，从而产生新的结构(如图2).

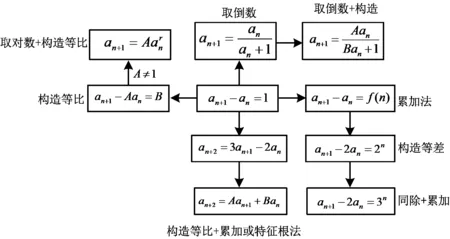
图2

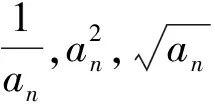
3)符号变化：将上述等式变为不等式(适当增加限制条件)，产生类等差和类等比结构.

评注逻辑推理核心素养既要关注知识和方法的生成过程，更要关注思维的发展和数学结构的变化.在这一环节中，通过原始结构“a1=1，an+1-an=1”，从形式、结构和符号变化产生新的结构，引发方法的变化，但“源”来同“根”.以此带领学生寻找逻辑推理的起点以及可以如何变化、变化生成什么等系列问题，实现核心素养的滋养过程.

环节3问题演变——逻辑推理的考查层次性.

演变1寻“源”——题干情境.

类型1数列类型确定，直接确定基本量加以解决.

已知Sn是等差(比)数列{an}的前n项和，给出以下两个条件之一：

条件1给定两项或项与项之间的关系，如：

1)am=a,an=b；

2)d=m(或q=m),ap=n；

3)am,an是方程x2+ax+b=0的两个根.

条件2给定项、前n项和的关系，如am=a,Sn=b.

类型2数列类型未知，需要通过转化确定数列类型，然后确定基本量.

已知Sn是数列{an}的前n项和，给出以下两个条件之一：

条件3给出函数型条件，如：

1)(n,an)在直线y=x上或y=Aqx上；

2) (n,Sn)在曲线y=Ax2+Bx或y=A(qx-1)上.

条件4给出递推条件，如：

1)a1=a,ean+1=ean+b或a1=a,lnan+1-lnan=b；

2)2an+1=an+an+2或ean，ean+1，ean+2成等比；

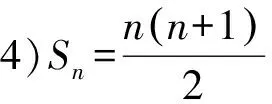
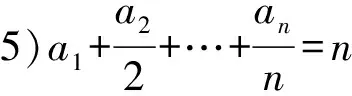
演变2问“流”——设问视角.

已知an=n，其中n∈N*.

第1层次加入常见裂项错位相消求和.

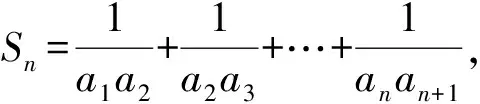
第2层次先求和后放缩.

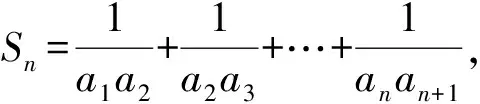
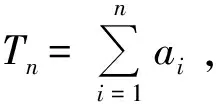
(2011年浙江省数学高考理科试题第19题改编)

第3层次先放缩后求和.

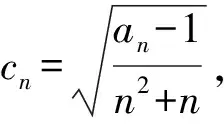
(2019年浙江省数学高考试题第20题改编)

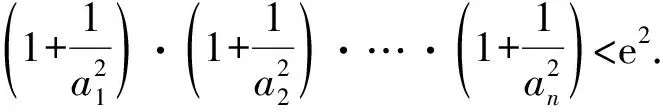
第4层次等式迁移到不等式——类等差(比).

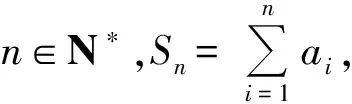
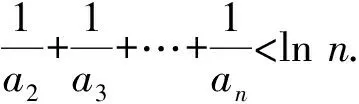
第7)小题的放缩方法与2015年浙江省数学高考理科试题第20题、2017年浙江省数学高考试题第22题密切相关.

评注逻辑推理的层次性是培养逻辑推理核心素养的重要要求，它可以实现逻辑的内在贯通，有效整合数学知识和数学思想方法.在这一环节中，通过数列类型已知和未知两大类以及项与项、项与和之间的关系等不同的角度寻找题“源”，再综合不同的方法设计设问方向，实现对题干情境和设问视角多角度、多层次演变.题“源”演变的关键是情境变化，题“问”演变的关键是视角变化和问题迁移，交互生成不同背景、不同难度的题干和设问，实现逻辑推理核心素养考查的层次性.

环节4“数列人”生成——逻辑推理的知识系统性.

1)学生活动：用“数列”知识和方法为卡通人添上“心脏”“大脑”和“四肢”等，让它成为你心中的“数列人”(图3).

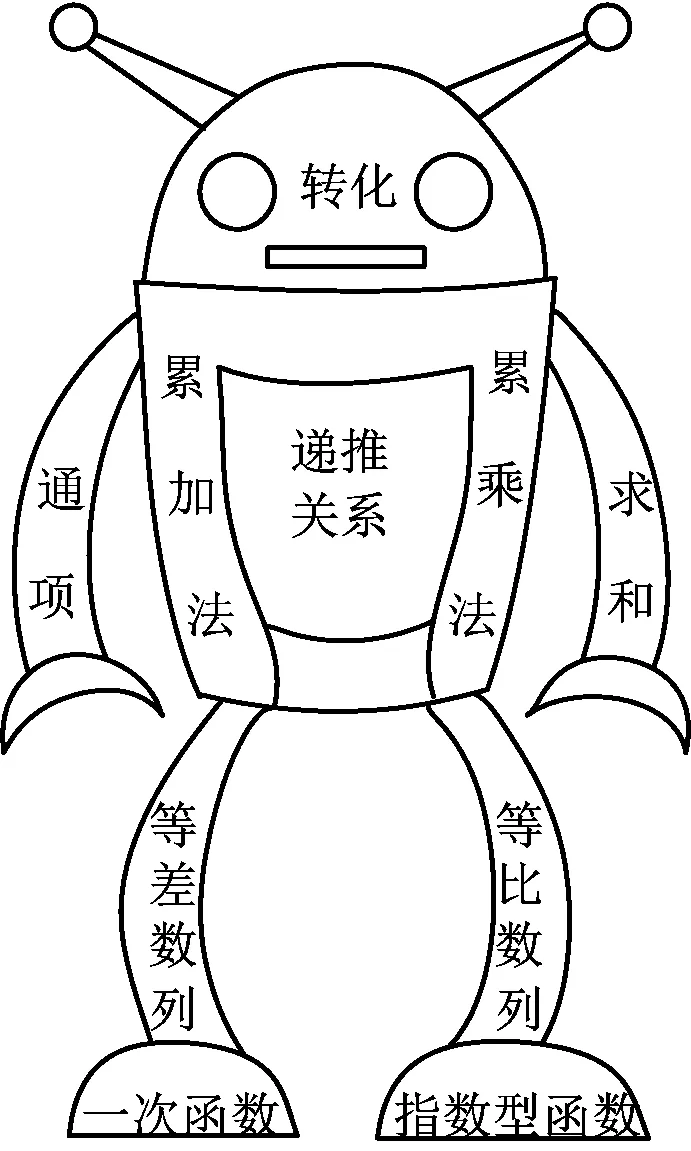
图3

2)师生讨论完善：“数列人”的心脏是递推关系，大脑是转化，大腿是两种特殊数列，两个抓手是通项与求和，基础是函数.学生还可以根据自身的知识掌握程度，进一步添加细化的内容，如可以画上手指、脉络等.

评注复习课必须立足于知识展开教学，作为章节的二轮复习，要让学生建立自主梳理知识和方法的习惯与意识.二轮复习的知识系统需要在一轮复习的基础上有所提升与突破，关键在于建立新的逻辑序.这一环节中，设计引导学生从数列的基础知识、标准模型、核心思想、关键能力等出发，由“粗”到“细”，通过“数列人”再次梳理知识，使逻辑链条不断清晰，逻辑推理素养呈现螺旋式上升.

环节5模型发散——逻辑思维的载体多样性.

师：请大家模仿本节课的结构，对照高中数学的主干知识，选择一章知识，从以下3个方面课后自行完成：

1)理一块：数学有骨架(知识)、脉络(方法)和肌肉(命题生长点)，你能否理清数学的主干知识的骨架、脉络和肌肉？

2)画一像：对于高中数学的主干知识，你能否模仿“数列人”画出“××人”？

3)命一题：能否选择一个知识点自行命制不同层次(识记、理解和应用)的试题？

评注数学知识的发展和变化的思维脉络具有一致性，当逻辑思维素养发展到一定层次时，思维模式可以进行移植、复制和迁移.不同的知识、不同的内容可以通过相同或相似的思维模式实现深度学习.

师：同学们，今天我不是主播，我只是一个主持人.通过今天的课堂和交流，我和我的团队希望带给大家一种数学二轮复习提升的策略：寻根觅亲，探寻知识的“根”与“芽”，审视命题的“源”与“流”.

2 几点思考

1)对本节课的教学设计和实施情况的反思.在设计本节课时，团队考虑了两方面因素:一是二轮复习，二是线上直播教学.二轮复习如何达成学生逻辑推理素养的目标？线上教学如何使学生从被动学到主动乐学、善学？

改变课堂模式，把主播变成主持.在课堂实施过程中，互动环节给予学生充分的展示空间，学生们用线条、文字、符号、式子构建自己的知识结构，上传各式各样的知识画像、递推关系和“数列人”.“以前从没听说过‘数列人’这个概念，没想到知识可以用这样的方法归纳！”直播课后，学生们给本节课的点赞和直播间内弹幕上刷满了“666”说明：我们的设计和课堂成功了！

2)对线上教学的思考.疫情按下了线下教学的暂停键，迫使广大教师从课堂走向屏幕.但线上直播教学的难度远大于线下教学，换舞台不减效果、从吸引人的眼球到影响人的学科发展成为困扰新“主播”的新难题.作为一次公益性线上直播活动，受众面很大，只有经过精心设计、团队打磨、有效活动，才能显现线上教学的魅力.而学科教学无论是线上还是线下，都需要以发展学生的学科能力为指向，本次直播就是以发展逻辑推理核心素养为目标进行的一次有效尝试.