圆台扰流换热器结构参数优化的数值模拟研究

2021-12-03赵振高建民徐亮席雷李云龙

西安交通大学学报 2021年12期

赵振,高建民,徐亮,席雷,李云龙

(西安交通大学机械制造系统工程国家重点实验室,710049,西安)

板式空气换热器是热能再利用的重要装备,具有结构紧凑、传热效率高、不易积灰及成本低等诸多优点,被广泛应用于炼油化工、航空航天、冶金及化肥等行业。许多学者对一些高效先进的扰流单元如半圆柱型肋片、仿生翅片及新型结构的流动传热性能等进行了研究[1-3]。在众多扰流单元中,球型结构由于流动阻力小、具有优良的换热性能等优势而备受关注[4-7]。而采用冲压成型工艺板片的换热器因具有结构强度高、传热效率高、制造成本低和无焊接热阻等特点而被重点关注[8-9],其结构特点为凹陷和凸起共同作用于气流扰动和加强换热。Hwang等通过瞬态液晶测量技术实验研究了布有周期性凹凸结构壁面的传热性能[10]。陈梦杰等采用数值模拟方法对新型冲孔球凸/球凹翅片结构流动传热特性进行了研究,结果表明冲孔球凸/球凹翅片综合热力性能优于多孔翅片[11]。王光辉等研究了凹陷凸起直径、深度及横向间距等对凹凸板换热器流动传热性能的影响[12]。

近年来,扰流结构的优化设计成为了热点研究。Zheng等对带离散斜肋的换热器进行数值模拟和敏感性分析,获得最高努塞尔数和摩擦系数下的结构参数[13]。徐亮等提出一种集热控、承载和轻量化于一体的新型冷却结构,并得到两类优化问题下的最优结构[14]。王斯民等采用多目标遗传优化算法对缠绕管式换热器几何结构进行了数值模拟研究,在连续响应面的基础上对原结构进行优化,得到3组优化结果[15]。夏春杰等采用遗传算法对蜂窝板换热器进行了多目标优化研究,探讨了各结构参数对蜂窝板各优化目标的影响并考察了各参数灵敏度[16]。Zheng等对锥形条涡发生器换热器开展了多目标优化,并采用非支配排序遗传算法2(NSGA-II)对目标函数进行优化,得到最优的几何参数[17]。

此外,随着未来换热器性能的提升,为了提高换热性能,其工质流动必将高速化,这将凸显出换热器内流体激振等问题,也对其抗振性能提出了更高的要求[18-19]。因此,需综合考虑高雷诺数下换热器结构的强度问题,发展一种高换热、高强度的新型结构,研究各结构参数对此结构流动换热性能和熵产的影响规律,并在此基础上对其进行多目标优化。

本文结合以上问题并基于高传热、低流阻的球型结构提出一种具有支撑作用的新型圆台结构,在高雷诺数下对冲压有圆台板片的换热器进行了实验研究,采用中心复合设计-响应面法对不同结构圆台扰流换热器开展了数值模拟研究,分析了当Re为10 000时,圆台径高比(D/H=2～4),圆台角度(α=0°～30°),流向间距比(Z1/D=1.5～2.5)和展向间距比(Z2/D=1.5～2.5)对圆台扰流换热器的综合热力性能、传热性能和熵产的影响规律,并对圆台结构进行了显著性分析和参数优化;拟合得到了有关逆流圆台扰流换热器通道综合热力性能、传热性能和熵产的经验关联式。研究结果可为未来新型圆台扰流换热器结构的优化设计提供参考和借鉴。

1 数值方法

1.1 研究对象

研究对象为逆流的圆台扰流换热器。图1给出了圆台扰流换热器的实验系统图。该实验系统可提供不同温度、压力和流量的冷热气流,主要包括冷、热气供气系统、进出口稳流段、消音装置、实验段及数据采集系统等,系统的详细介绍见文献[20]。图2给出了具体的研究对象,由图2a可知,圆台结构的排布沿流向为凹陷和凸起交叉分布,由于采用冲压成型工艺板片结构的特殊性,冷气侧的圆台凸起即为热气侧的圆台凹坑。由图2b可知,圆台结构具有充当通道支撑,加强换热器结构强度的作用;冲压有圆台结构的板片厚度为1 mm,冷气、热气通道的长度(L)和宽度(L)均为600 mm,通道的高度为2倍圆台高度2H,圆台的直径D为30 mm,高度H为10 mm,角度α为15°,相邻的圆台结构流向间距Z1为60 mm,展向间距Z2为60 mm,并以此为参考结构。为探索不同圆台纵向间距、流向间距、底部直径和角度对流动换热的影响,根据本课题组前期有关圆台扰流换热器的研究[21],在雷诺数固定为10 000时,研究不同圆台结构参数的影响,将D、Z1和Z2转化为无量纲D/H、Z1/D和Z2/D,固定L和H不变,D/H的变化范围为2～4,α的变化范围为0°～30°,Z1/D的变化范围为1.5～2.5,Z2/D的变化范围为1.5～2.5。

图1 圆台扰流换热器的实验系统图

(a)3D模型

1.2 计算方法及边界条件

采用商用CFD软件CFX进行数值模拟。本文所考虑的流动和换热现象假设为稳定、单相、定常且三维的。采用基于有限元的有限差分法来离散控制方程,求解三维可压缩的雷诺时均N-S方程,方程中的扩散项、源项和对流项均采用高精度的离散格式进行离散,数值模拟的整体残差水平设置为10-6。

根据本课题组前期有关扰流通道的研究[22-23]可知,在标准k-ε、k-ω和SSTk-ω等3种常用的湍流模型中,SSTk-ω湍流模型对扰流通道传热性能的预测精度最高,与实验数据最吻合。SSTk-ω湍流模型在主流区采用标准k-ε模型,在近壁区采用k-ω模型,较其他湍流模型而言能更准确地预测扰流通道的传热性能。同时,为保证不同类型扰流通道的数值模拟结果具有可对比性,其湍流模型应该一致。因此,本文针对圆台扰流通道的数值模拟也采用了SSTk-ω湍流模型。

图3给出了具体的数值模型,为了简化计算,选取了一个周期性通道,如图2a的红色虚线所示。由图2可知,通道高度为H,宽度为Z2,长度为L,通道两侧为周期性边界条件,通道上壁面为对称边界条件,通道下壁面为加热壁面,给定均匀的热流密度。为消除通道入口和出口对冷却流体流动和换热的影响,在通道进、出口分别延长了200 mm的稳流段。计算边界条件具体如下:进口给定速度,温度为300 K,法向均匀进气,进口湍流度为5%。出口边界条件为压力出口,其值固定为一个标准大气压。通道下壁面给定1 000 W/m的热流密度。参考文献[24],上述设置是合理的。

图3 数值模型

图4所示为圆台扰流通道的网格模型示意图。网格划分采用ANSYS ICEM完成,全部采用结构化网格。为适应SSTk-ω模型,对近壁面区域网格进行了细化处理,近壁面第一层网格尺寸为0.001 mm,网格增长率为1.2,边界层的层数为15,保证无量纲近壁距离y+小于1。

图4 网格示意图

1.3 数据处理

通道入口雷诺数的定义为

Re=uiD/ν

(1)

式中:ui为通道入口速度;D为当量直径,取值通道高度2H;ν为气流的运动黏度。

加热壁面当地努塞尔数的定义如下

Nu=qD/[λ(Tw-Tf)]

(2)

式中:Tw为壁面当地温度,当Tw为加热壁面的平均温度时,Nu为加热壁面的平均努塞尔数;Tf为参考温度,文中选取为进出口温度的平均值;q为加热壁面的热流密度;λ为空气的导热系数。

通道的摩擦系数f定义如下

(3)

式中:Δp为通道进出口压差;ρ为冷气密度。

通道的体积熵产率[25]定义如下

S‴g=S‴g,Δp+S‴g,ΔT

(4)

(5)

(6)

式中:S‴g,ΔT为换热引起的熵产;S‴g,Δp为流动摩擦引起的熵产;T为当地温度;μ为空气的动力黏度,u、v和w分别为x、y和z方向的速度分量。

通道的总熵产定义如下

Sg=∭ΩS‴g,ΔTdV+∭ΩS‴g,ΔpdV

(7)

式中:V为流体域的体积。

评价通道性能的有3个指标,分别为综合热力性能、传热性能和熵产。其中传热性能可表示为Nu/Nu0,具体含义为通道的努塞尔数比,熵产可表示为Sg/Sg,0,具体含义为通道的总熵产比,综合热力性能可表示为G,定义如下

G=(Nu/Nu0)/(f/f0)1/3

(8)

式中:Nu0、f0和Sg,0分别为光滑通道的努塞尔数、摩擦系数和总熵产。G>1意味着通道相对于光滑通道具有更好的综合热力性能,Nu/Nu0>1意味着通道相对于光滑通道具有更好的换热性能,Sg/Sg,0>1意味着圆台扰流通道相较于光滑通道具有更大的熵产。

1.4 数值方法验证

为保证数值模拟方法的可靠性和经济性,本小节对圆台扰流通道进行了网格无关性验证,同时对比分析了数值和实验结果。图5给出了不同网格数下参考通道的努塞尔数和压差,从图中可知,5种网格划分策略,即网格数为103万、121万、145万、167万和198万时,通道的平均努塞尔数和压差均随网格数的增大而逐渐增大,当网格数为167万和198万时,通道的平均努塞尔数和压差的差异均小于2%,即达到了网格无关性的要求。因此,不同圆台结构的通道都将采用与第四套网格相同的网格划分策略。

图5 网格无关性验证

图6为圆台扰流通道的计算结果与实验结果的对比,图6a为不同雷诺数时通道努塞尔数比的实验结果和数值结果的对比,并给出了实验结果5%的误差曲线。从图中可以看出,两者的分布极为相似且通道的平均Nu误差在5%以内。图6b给出了不同Re下通道摩擦系数比的实验值和模拟值,两者的最大误差也低于5%。这说明SSTk-ω模型可以较为准确地模拟圆台扰流通道中的流动和换热情况。综上,本文有关圆台扰流通道流动和换热特性研究的数值方法是可靠的。

(a)通道的努塞尔数比

2 结果分析与讨论

2.1 结构参数对流动、传热性能和熵产的影响

图7给出了圆台扰流通道的涡核分布和速度旋涡强度。ANSYS-CFD-Post中的λ2准则可以直观地显示涡核,是目前最可靠、最准确的涡核识别方法之一,文中采用此方法进行涡核识别。从图7可以看出,基本上所有圆台扰流通道的共同点为通道的涡核集中分布在圆台凹陷的底部、第一个圆台凸起的两侧和圆台凸起的下游区域。当D/H为2时,如图7a所示,通道的流向和展向的圆台分布均较为密集,因此,气流的扰动较为剧烈,这增大了圆台扰流通道的涡核和旋涡强度;值得注意的是,随着D/H增大,通道的涡核会逐渐较少。而当圆台角度α从0°增大到30°时,如图7b所示,通道在第一个圆台凸起区域的涡核会增加,而别的区域的涡核会减少;此外,随着圆台角度的增大,整体的旋涡强度呈增大趋势。当圆台的流向间距发生变化时,如图7c所示,通道中圆台附近的涡核会随着流向间距的增大而增加。而当圆台展向间距Z2/D从1.5增大到2.5时,如图7d所示,通道中圆台附近的涡核和旋涡强度会随着展向间距的增大而呈现减小的趋势。

(a)不同径高比

图8给出了圆台扰流通道的当地努塞尔数分布云图。从图8可以看出,所有圆台扰流通道的共同点为高努塞尔数区域主要分布在通道进口、第一个圆台凸起的前缘和两侧等区域。气流刚进入通道的时候由于还未形成边界层而存在较高的换热系数;第一个圆台凸起的迎风面由于气流的直接冲刷,流体之间形成强烈的混合,形成较高的换热系数;来流经过圆台凸起时,因形成的马蹄涡不断冲刷底壁面提高了附近区域的换热系数。另一方面,低努塞尔数的区域主要分布在凸起的尾流区域和凹陷的前缘附近。

当结构参数D/H发生变化时,即D/H从2增大到4时,如图8a所示,圆台的流向和展向排布均发生了变化;当D/H为2时,通道的流向方向圆台分布较为密集,因此,换热也较为充分,这是由于密集的排列加强了气流的扰动,从而增强了换热;值得注意的是,当D/H为3时,第一个圆台凹陷会有较强的换热。而当圆台角度α从0°增大到30°时,如图8b所示,第一个圆台凸起周边的强换热区域会随着圆台角度的增大呈增大趋势;此外,当α为15°时,第一个圆台凹陷具有最强的换热效果。当Z1/D从1.5增大到2.5时,如图8c所示,流向的圆台个数从14个减少到了8个;随着圆台个数的减少,第一个圆台凹陷底部的强换热区域逐渐减小,这是由于随着圆台流向间距的增大,气流的扰动逐渐平稳。而当Z2/D从1.5向2.5增大时,如图8d所示,圆台的展向间距逐渐增大;随着展向间距的增大,第一个圆台凹陷底部的换热依次减弱,这是展向间距的增大减小气流扰动造成的;值得注意的是,当Z2/D为1.5时,第一个圆台凹陷区域出现了强换热区,这可能是由于较小的圆台展向间距使得气流出现激烈的扰动,削弱了边界层加强换热。

(a)不同径高比

图9给出了圆台扰流通道的当地体积熵产率的分布云图。从图9可以看出,所有圆台扰流通道的共同点为高熵产的区域主要分布在圆台的两侧(除了第一个圆台凹陷)。这是由于来流经过圆台时,在圆台凸起的两侧产生马蹄涡,而在圆台凸起的下游和圆台凹陷底部区域形成二次流回流,这会导致圆台的两侧区域附近的流体有较强的换热和流动混合;而传热熵产主要来自流体和壁面的温差,摩擦熵产主要是由摩擦流动引起的,因此,圆台的两侧区域有较高的熵产。值得注意的是,第一个圆台凹陷对附近流体的流动影响较小,因此,未出现像圆台两侧那样的高熵产区域。另一方面,低熵产的区域主要分布在圆台凹陷的底部区域,这是由于圆台凹陷底部区域的二次流回流抑制了气流的流动和传热,因此,熵产也较低。

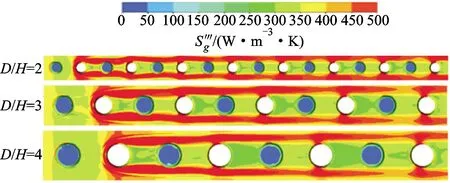
(a)不同径高比

当结构参数D/H发生变化时,即D/H从2增大到4时,如图9a所示,圆台的排布在流向和展向均变得稀疏;当D/H为2时,通道流向和展向的圆台分布均较为密集,因此,流动和换热也较为充分,这增强了该通道的熵产;值得注意的是,当D/H增大时,圆台两侧的强熵产区域也会增大。而当α从0°增大到30°时,如图9b所示,圆台凹陷底部的弱熵产区域会随着圆台角度的增大呈减小趋势;此外,随着圆台角度的增大,圆台两侧的强熵产区域也会略微减小。当圆台的流向间距发生变化时,如图9c所示,圆台两侧的强熵产区域会随着流向间距的增大而减小。而当圆台展向间距Z2/D从1.5增大到2.5时,如图9d所示,圆台两侧的强熵产区域会随着展向间距的增大而呈现明显的减小趋势。

2.2 结构参数的显著性分析

采用中心复合设计(CCD)-响应面法(RSM)分析不同响应(G、Nu/Nu0和Sg/Sg,0)下输入参数(D/H、α、Z1/D和Z2/D)的显著性。为保证响应面模型的计算精度,采用拟合精确度R2来验证近似模型的准确性。表1给出了不同响应下响应面模型的R2,可以看出拟合精度均在0.93以上,因此该模型能够很好地对实际模型进行近似。图10、图11和图12分别给出了G、Nu/Nu0和Sg/Sg,0正态效应图和Pareto效应图。图中,A、B、C、D分别表示设计变量D/H、α、Z1/D、Z2/D,其中A、B、C、D代表线性项,AA、BB、CC和DD代表平方项,AB、AC、AD、BC、BD和CD代表交互项。在正态效应图中,各因子的效应由小到大(正负号考虑在内)排成序列,并将这些效应点标在正态概率图上。在Pareto效应图中,正效应分布在红线右方,负效应分布在红线左方。从图10可以看出,由灵敏度水平从高到低排列的G的有效项是α、Z1/D、(D/H)α和Z2/D,其中α、Z1/D和Z2/D对G有正效应,(D/H)α对G有负效应。类似地,如图11所示,由高到低的灵敏度水平排序的Nu/Nu0的有效项为Z2/D、D/H、(Z2/D)(Z2/D)、α、α(Z1/D)、α(Z2/D)和Z1/D,其中(Z2/D)(Z2/D)、α、α(Z2/D)和Z1/D对Nu/Nu0有正效应,而Z2/D、D/H和α(Z1/D)对Nu/Nu0有负效应。相应地,如图12所示,由高到低的灵敏度水平排序的Sg/Sg,0的有效项为Z2/D、α、α(Z2/D)、D/H、(D/H)α、Z1/D、(D/H)(Z2/D)和(Z2/D)(Z2/D),其中Z2/D、α、D/H和Z1/D对Sg/Sg,0有负效应,而α(Z2/D)、(D/H)α、(D/H)(Z2/D)和(Z2/D)(Z2/D)对Sg/Sg,0有正效应。综上所述,在4个影响参数中,α是影响G的最显著参数,其次是Z1/D、Z2/D和D/H;Z2/D对Nu/Nu0的影响最显著,其次是D/H、α和Z1/D;对Sg/Sg,0影响最显著的是Z2/D,其次是α、D/H和Z1/D。

表1 响应面模型拟合精度

(a)Pareto效应图

2.3 圆台结构的参数优化

在响应面模型的基础上,对结构参数进行了优化,以提高圆台扰流通道的综合热力性能和换热性能,降低熵产。优化结果如图13所示,分为单目标优化和多目标优化,图13a是以综合热力性能最好为优化目标;图13b是以传热性能最好为优化目标;图13c是以熵产最低为优化目标;图13d是以最优传热性能和最低熵产为目标的多目标优化。图中,每个单元格中的黑色曲线表示当其他输入参数保持不变时,响应变量或复合期望值随其中一个输入参数的变化,水平的蓝色虚线表示当前响应值,垂直的红色实线表示输入参数的相应级别。图中纵坐标给出了优化响应值的分布范围,横坐标为输入参数及其空间变化。以实验的圆台扰流通道为参考通道,即D/H为3、α为15°、Z1/D为2且Z2/D为2时,通道的G、Nu/Nu0和Sg/Sg,0分别为0.81、1.43和1.10。以综合热力性能最好为优化目标,可得到圆台参数D/H为2、α为30°、Z1/D为2.5和Z2/D为2.5时,圆台通道的G为0.993 5,与参考通道相比,优化得到的通道综合热力性能提高了22.65%。以传热性能最好为优化目标,可得到圆台参数D/H为2、α为16.060 6°、Z1/D为2.247 5和Z2/D为1.5时,圆台通道的Nu/Nu0为2.060 7,与参考通道相比,优化得到的通道传热系数提高了44.11%。以最低熵产为优化目标,得到的最优圆台参数D/H为2.303、α为30°、Z1/D为2.5和Z2/D为2.227 3,圆台通道的Sg/Sg,0为0.789 4,与参考通道相比,优化得到的通道熵产降低了28.24%。当以传热性能和最低熵产为目标进行多目标优化时,最终得到最优的圆台参数D/H为2.303、α为30°、Z1/D为2.247 5和Z2/D为1.5,通道的Nu/Nu0为1.988 3,Sg/Sg,0为1.239 6。与参考通道相比,优化得到的通道的传热性能提高了39.04%,但其熵产增加了12.69%。这说明当采用多目标优化时,有时并不能得到所有目标参数的最优解,需要综合考虑各目标参数的权重。表2给出了具体的优化结果。

(a)最大化G

图14给出了不同优化结果下沿流向方向第三个周期性结构通道的表面流线和温度分布云图,其中图14a为参考通道的表面流线,图14b为最大G通道的表面流线,图14c为最大Nu/Nu0通道的表面流线,图14d为最小Sg/Sg,0通道的表面流线,图14e为多目标优化通道的表面流线。从图中可知,这5种通道的表面流线和温度云图分布均不同,参考通道在凹陷的上游和凸起的下游均存在较大的旋涡,而4种优化通道的旋涡均得到了改善,旋涡的改善会减小通道的摩擦阻力进而减小摩擦熵产;同时,4种优化通道在凹坑底部和凸起下游的高温度分布区域较参考通道均减少,这会降低通道表面的平均温度并减小传热温差,从而增强换热和降低传热熵产。横向比较而言,结合表2,参考通道具有最低的综合热力性能,多目标优化相比最大G得到的圆台扰流通道,其综合热力性能降低8.71%;以Sg/Sg,0最小为目标得到的通道较参考通道的传热性能降低1.38%,多目标优化较Nu/Nu0最大得到的通道的传热性能低3.51%;不同目标优化下通道的熵产从小到大依次为最小Sg/Sg,0、最大G、参考通道、多目标优化和最大Nu/Nu0通道,其中,多目标优化得到的通道与最小Sg/Sg,0得到的通道相比熵产增大了57.03%。

表2 圆台扰流通道的优化结果

(a)参考通道的表面流线

2.4 关联式拟合

圆台扰流通道的综合热力性能、传热性能和熵产关联式对于未来新型圆台扰流换热器冷却结构的设计具有重要的指导意义。响应面方法(RSM)通过数值实验和分析找到了输出和输入变量之间函数关系的自适应近似。考虑所有线性项、平方项和相互作用项的二阶RSM模型能够以较高的精度逼近大部分响应,因此本文采用这种模型。模型的一般形式如下

(9)

式中:B0表示截距;Bi、Bii和Bij分别表示线性、正方形和交互项的回归系数;xi和xj是设计变量;y是响应变量;ε是预测误差。

式(9)的适用范围为:2≤D/H≤4,0°≤α≤15°,1.5≤Z1/D≤2.5,1.5≤Z2/D≤2.5。

表3给出了圆台扰流通道的综合热力性能、传热性能和熵产拟合公式的系数,图15～图17给出了圆台扰流通道综合热力性能、传热性能和熵产关联式拟合的偏差分布。对于综合热力性能的关联式,最大偏差为6.52%,平均偏差为2.46%。对于传热性能关联式,最大偏差为8.27%,平均偏差为3.86%。对于熵产关联式,最大偏差为14.85%,平均偏差为5.39%。这表明本文拟合得到的关联式能够准确地预测圆台扰流通道的综合热力性能、传热性能和熵产,可以为圆台结构在未来先进换热器通道中的应用提供参考和借鉴。