新高考背景下结构不良问题在新授课中的应用

卢依婷

(杭州第二中学钱江学校，浙江 杭州 311215)

1 问题提出

2020年山东省数学高考贯彻了“低起点，多层次，高落差”的调控策略，结构不良问题首次亮相．结构不良问题具有条件缺失、选择多样、结果开放等特点，能够使学生在解决问题的过程中，根据具体情境，从多个角度分析，考虑多个可能，寻找不同路径，提出多种解决方法，以考查学生思维的系统性、灵活性、深刻性、创造性，促进学生素养的形成和能力的提升．学生在学习过程中，大多遇到的是结构良好的问题，问题的指向性明确，解决问题的思想方法自成一套．而在新高考选拔性要求高的背景下，势必要一改过去的习惯，大胆设问，小心求证．因此，如何在课堂实践中渗透结构不良问题，从而提高教学实效性，帮助学生发散思维，促进学生素养的养成和能力的提升，值得一线教师探究．

2 问题分析

结构良好问题是指问题的初始状态、目标状态和算子都是完整的，而结构不良问题则是三者中至少有一个没有明确界定的问题[1]．结构不良问题要求学生在条件模糊的情境中，主动提出问题，完成开放性的探究任务．但本文并不是研究如何在课堂上学会结构不良问题的解决方法，而是致力于突破常规新授课的设计，使得结构不良问题不仅仅是课堂练习，还可作为教学的某一环节．

康托尔说：“数学的本质在于它的自由．”在教学中，数学的定理、法则、公式等理应注重让学生自主发现．数学教育的意义在于使学生学会思考，因此，教师在教学设计时，需在“如何使学生想得到”上多下功夫，提高处理“预设”与“生成”关系的能力，力争通过有效提问促使学生实现知识的自主发现．那么，如何才能将结构不良问题有效应用于新授课中，使学生具有成长型思维模式，增强其学习的内在动机呢？如改变问题结构，教师可构造条件不清晰、某个条件不清晰或条件结论都不清晰但供选择的不同程度的开放性问题，有层次地展开思考活动，建立局部逻辑体系[2]．在备课时，教师需有结合结构不良问题进行教学的意识，思考每一课中的哪个知识点可应用该结构，并做好预设．

通过学习可知：一些数学概念可以通过充要条件给出它的等价定义，通过充分条件给出它的判定定理，通过必要条件给出它的性质定理．因此，教师可从命题角度出发，将已知命题的条件、结论与否定后的条件、结论放在一起作为选项，暗示学生从充分必要性着手自由重组命题，通过演绎推理证明命题．对于多条件的命题，可考虑删减条件，或增添易混淆的相关条件，形成新命题．简而言之，该环节设计的基本流程有3点——提、构、评，笔者称之为TGP教学模型．首先，根据具体教学情境，提取关键条件；其次，构造结构不良问题，让学生自主探究；最后，师生共同评价，教师总结．以下是笔者的两个教学案例，供各位同仁参考．

3 解决案例

3.1 案例1

在“函数的零点与方程的根”一课中，笔者以零点存在定理为背景，按照“概念—定理—应用”的线索，设置了4个教学环节，环环相扣，自然衔接．为进一步加深学生对定理的理解，笔者在独立思考、合作探究环节中，应用TGP模型，把分析环节中得到的与零点存在定理相关的条件提取出来，设置了体现各条件、结论内在关系的结构不良问题，让学生重构命题并讨论评价．最后，通过改变条件，得到判断零点唯一的一个充分条件．

探究1请同学们从下列条件中任选3个，组成一个命题，并判断真假，若是假命题，则请通过图像说明理由．

①f(a)f(b)<0；

②函数y=f(x)在区间[a,b]上连续；

③函数y=f(x)在区间(a,b)内有零点；

④f(x)在区间(a,b)内有且仅有一个零点；

⑤f(a)f(b)≥0.

笔者先给出探究1，让学生竭尽所能地组合条件成为有意义的命题，并通过小组讨论互相判断对方命题的真假性．待学生充分讨论后，再给出探究2．

探究2请同学们从下列条件中任选3个，组成一个命题，并判断真假，若是假命题，则请通过图像说明理由．

①f(a)f(b)<0；

②函数y=f(x)在区间[a,b]上连续；

③函数y=f(x)在区间(a,b)内有零点；

④f(x)在区间(a,b)内有且仅有一个零点；

⑤f(a)f(b)≥0；

⑥函数y=f(x)在区间(a,b)内无零点.

探究2在探究1的基础上增加了条件⑥，即函数y=f(x)在区间(a,b)内无零点．在笔者给出探究2后，学生的探究热情更加高涨，讨论氛围浓厚，仿佛在打游戏通关，升级后打高级副本．笔者乘机让一位学生上台写下自己小组的探究成果，并在讨论过程中， 引导学生若有补充则可上台展示；若认为有写得不对的，则也可上台举反例推翻．

生1上台书写的4个命题都是假命题，并且给出了正确的反例图像．

命题1若①②，则④(反例如图1).

图1 图2

命题2若②⑤，则④(反例如图2).

命题3若②⑤，则⑥(反例如图3).

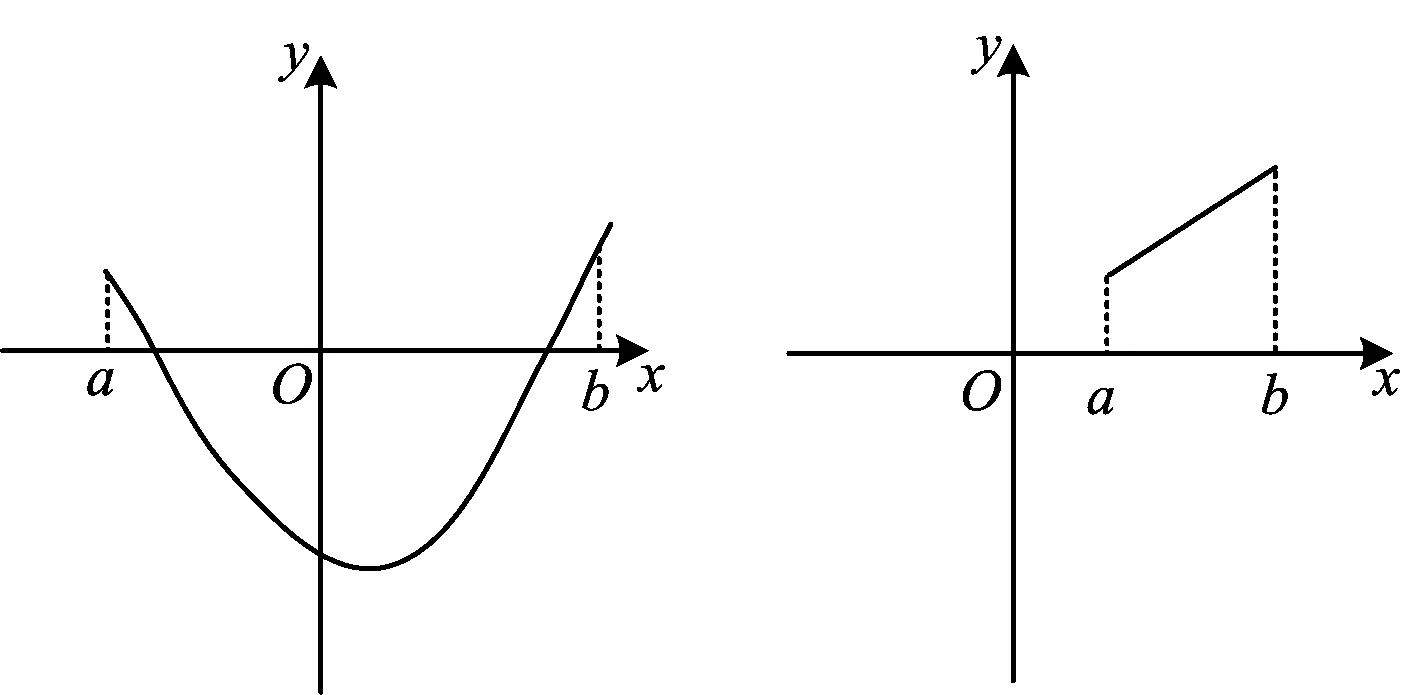
图3 图4

命题4若②⑤，则③(反例如图4).

生2在生1的基础上进行补充，得到以下命题．

命题5若②③，则①(反例如图3).

命题6若①③，则②(反例如图5).

图5 图6

笔者发现两位学生在黑板上书写的命题都是假命题，于是面向全体学生问：“全是假命题吗？是否有真命题？”生3立马举手上台补充了3个命题．

命题7若②⑥，则⑤.

命题8若②④，则①．

命题9若③④，则⑥．

生3认为命题7和命题8均为真命题，而命题9条件与结论矛盾，显然为假命题，故图略．对于命题8，生4认为这是假命题，上台举出反例如图6．对于命题7，生4也认为是假命题，尝试着举出反例，但没找出破绽．这个命题引起了全班争议，大部分学生认为是假命题却未找出反例．由于时间有限，笔者说明了命题7为真命题的理由，解决了学生纠结的点．

该探究环节的设计意图是使学生通过几个重要条件的自由组合，感悟各个条件间的充分必要性如何．借助一些正反例研究函数零点存在的条件，但千万不要把充分条件当成必要条件，且需注意零点存在定理无法判定零点个数，因此，自然想到零点唯一的充分条件．另外，学生在这两个探究中被调动了积极性，为探究3的顺利开展做铺垫．笔者引导学生通过数学的方式，从逻辑严密性的角度对定理中两个条件的充分性、必要性进行考查，抓住了发展学生数学学科逻辑推理、数学抽象、直观想象等核心素养的契机．

探究3请同学们从除④外的条件中任选3个作为条件，结论为④，组成一个真命题．

①f(a)f(b)<0；

②函数y=f(x)在区间[a,b]上连续；

③函数y=f(x)在区间(a,b)内有零点；

④f(x)在区间(a,b)内有且仅有一个零点；

⑤f(a)f(b)≥0；

⑥函数y=f(x)在[a,b]上是单调函数.

由上述探究，学生快速得出以①②⑥作为条件，可推出④．即如果函数y=f(x)在[a,b]上，图像是连续的，并且在闭区间的两个端点上的函数值互异，即f(a)f(b)<0，且是单调函数，那么，这个函数在(a,b)内必有唯一的零点．该处并未像前两个探究那样如此开放，而是更像一个选择题.当然此处可以让学生自由选择条件组成命题，通过判断真假得到相关结论．但由于课堂时间有限，笔者舍弃了该处的开放，其实关于零点唯一的充分条件的探究大有文章可做．

3.2 案例2

解三角形是由已知的边角确定未知边角元素的过程．三角形的6个元素中知道几个能解三角形？有哪些类型？笔者再次应用TGP模型，将三角形的6个元素提取出来作为条件，引入结构不良问题，让学生自己选择条件构造命题，完成求解并整理各种情形．以下呈现的是例题及教师预设的内容．

例1已知△ABC的内角A,B,C的对边分别为a,b,c，请在以下6个条件中选择3个作为条件，若可以解三角形，则请作答；若不行，则请说明理由．

情形1若选择①②③，相当于已知三角形的3条边长，则可利用余弦定理得到3个角的大小．

情形2若选择①②④或①②⑤或②③⑤或②③⑥或①③④或①③⑥，相当于已知两边长和其中一边的对角，则可利用正弦定理得到第三边的对角，且需要判断解是否唯一．

情形3若选择①②⑥或②③④或①③⑤，相当于已知两边长和第三边的对角，则可利用余弦定理求出第三边，且需要判断解是否唯一．

情形4若选择①④⑤或②④⑤或②⑤⑥或③⑤⑥或①④⑥或③④⑥，相当于已知两角和其中一角的对边，则可利用正弦定理得到第三个角所对应的边长，再进一步求解．

情形5若选择③④⑤或①⑤⑥或②④⑥，相当于已知两角和第三个角的对边，则可利用正弦定理求出第三边．

情形6若选择④⑤⑥，相当于已知3个角的大小，则此时三角形是不确定的．

4 行动反思

4.1 增强使用结构不良问题授新课的意识

在数学教学中，结构不良问题应用广泛，其通常以目标不清晰的问题形式呈现，但在该情境下学生是接受学习，不符合新课程“一切为了学生的发展”理念．若希望学生变被动为主动，成为信息加工者进行探究学习，则教师需有意识地重视和改进数学的教学．备课时应基于学生的原有认知结构，从学生思维的最近发展区出发，思考在何处可巧妙应用结构不良问题引发认知冲突，并做好预设．在探究过程中基于构造的几个问题，不断启发学生，提高学生思维的敏捷性，促进学生认知的飞跃和提升，从而在数学教学中发展学生的核心素养，体现以生为本的先进教育理念．

4.2 巧用结构不良问题，帮助学生理解新知识的本质

问题是认知冲突的“导火索”，提问对学生的思维提升有显著效果．当教师提出问题恰到好处时，将会激发学生的探究热情，有利于发展他们的数学学科核心素养[3]．TGP模型作为一种有效的教学策略，是培养学生逻辑思维的发展路径．该模型不仅可通过探究用于概念辨析和深化理解，而且能够将多题合一，使学生在体验命题者意图的同时，对数学知识的来龙去脉有本质性理解．其解决过程能有效地激发学生的求知欲、帮助学生多角度把握问题本质、追寻知识背后的价值、形成跨学科综合解决问题的关键能力．好的问题是思维发展的助推器，因此其也可结合问题链的使用灵活、课外预设、整体性等特性，体现思维脉络，实现真正意义上“数学是自然的，数学是清楚的”．

4.3 注重新授课的时效，紧握新高考趋势

课堂是提升数学核心素养的第一阵地，而数学教学要用数学知识浸润核心素养的形成．在新高考选拔性要求高的背景下，结构不良试题增加了问题的情境性，符合通过情境与情境活动来考查学生的学科能力的要求．在新授课中引入结构不良问题，能够弥补传统教学的不足，活化“死知识”，有利于调动学生的思维，高度激发学生学习的积极性，使学生经历从感知到理解顿悟的过程．此外，教师应把握好新高考趋势，通过调整二者的部分结构进行结合，打破固有观念，多策略创新教学，用层次递进的结构不良问题探究驱动学生循序渐进地思考，用整体教学追求直观和逻辑的融合发展，最大限度地发挥数学知识的育人功能．