基于相关分析的乙醇偶合制备C4烯烃研究

张子奥，赵秋梦，刘晨旭

（燕山大学 里仁学院，河北秦皇岛 066000）

C4烯烃广泛应用于化工及医药产品的生产，乙醇是生产制备C4烯烃的原料。传统的生产方法采用化石能源为原料，但随着化石能源产量的短缺及对环境影响的加重，能源的供给逐渐趋向多元化，开发新型的清洁能源显得愈加紧迫。乙醇可以通过生物质发酵制备，来源广泛、绿色清洁，以其为原材料生产高附加值的C4烯烃具有巨大的应用前景及经济效益，受到国内外广泛关注。

在制备过程中，C4烯烃的选择性和C4烯烃收率将受到催化剂组合与温度的影响。本文以2021年全国大学生数学建模竞赛赛题B[1]所提供的实验数据为基础，建立数学模型设计催化剂组合，探索乙醇催化偶合制备C4烯烃的最佳工艺条件。

1 实验方法

1.1 相关分析

当一个或几个相互联系的变量取一定数值时，与之相对应的另一变量的值虽然不确定，但仍按某种规律在一定的范围内变化，变量间的这种相互关系称为具有不确定性的相关关系[2]。相关关系按相关形式可分为线性相关和非线性相关。相关分析是用一个指标来表明现象间相互依存关系的密切程度。单相关分析是对两个变量之间的相关程度进行分析，单相关分析所用的指标称为单相关系数，简称相关系数。

1.2 多因素方差分析模型

多因素方差分析有2种类型[3]：（1）无交互作用的多因素方差分析，假定因素效应之间是相互独立的，不存在相互关系；（2）有交互作用的多因素方差分析，假定因素之间的结合会产生出一种新的效应。在本研究中，假定各个因素间有交互作用，选择有交互作用的多因素方差分析。

1.3 非线性回归模型

如果回归模型的因变量是自变量的一次以上函数形式，回归规律在图形上表现为形态各异的各种曲线，那么这类模型则称为非线性回归模型[4-5]。已知C4烯烃收率=乙醇转化率×C4烯烃选择性，在本研究中，乙醇浓度和温度与C4烯烃收率并不呈现严格的线性关系，故选择非线性回归模型来模拟两种因素对C4烯烃收率的影响。

2 结果与分析

2.1 确定相关分析的计算方式

利用MATLAB做散点图分析温度与乙醇转化率和C4烯烃选择性的关系，发现温度与乙醇转化率、C4烯烃的选择性分别呈一定的线性关系。以催化剂组合A1（200 mg 1wt%Co/SiO2-200 mg羟基磷灰石（HAP）-乙醇1.68 mL/min）为例，利用MATLAB做出的散点图所呈现的线性关系如图1所示。

图1 C4烯烃选择性、乙醇转化率在不同温度下的散点图

线性相关分析的计算方式有Pearson相关系数（适用于定量数据，且数据满足正态分布）和Spearman相关系数（数据不满足正态分布时使用）2种[2]。以下进行数据正态性检验，并根据检验结果计算相关系数。

（1）正态性检验。对实验数据进行Shapiro-Wilk（小数据样本，一般样本数5 000以下，简称SW）检验，查看实验数据样本显著性。当实验数据呈现显著性（P＜0.05或0.01，严格为0.01，不严格为0.05）时，说明不符合正态分布；当不呈现出显著性（P＞0.05或0.01，严格为0.05，不严格为0.01）时，说明符合正态分布。

以催化剂组合A1为例进行Shapiro-Wilk正态性检验，结果如表1所示。结果表明，实验数据满足正态分布，因此选用Pearson相关系数证明相关性。

表1 Shapiro-Wilk正态性检验

（2）Pearson分析

Pearson相关系数公式为：

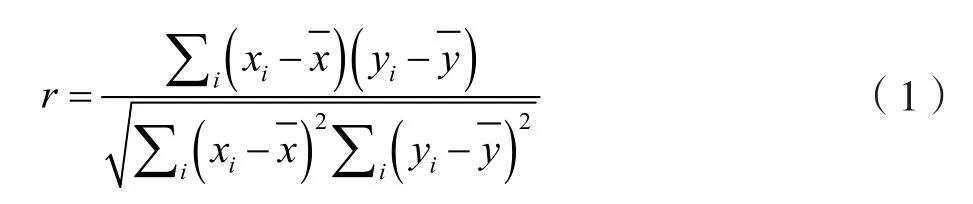
式中：xi为第i个时间；为此组时间的平均值；yi为第i个时间对应的乙醇转化率或C4烯烃选择性；为乙醇转化率或C4烯烃选择性的平均值。

利用MPai 2.1平台计算得出Pearson相关系数，乙醇转化率与时间的相关系数为-0.966，P=0.000＜0.01；C4烯烃选择性与时间的相关系数为0.215，P=0.643＞0.05。说明在温度与催化剂确定的情况下，乙醇转化率与时间呈很强的负相关性，C4烯烃选择性与时间不相关。

2.2 双因素方差分析

乙醇浓度和Co负载量对乙醇转化率检验结果如表2所示。结果表明，乙醇浓度与Co负载量×乙醇浓度的交互作用对乙醇转化率有较大的影响，而Co负载量对乙醇转化率的影响较为微小。

表2 乙醇浓度和Co负载量对乙醇转化率的影响

乙醇浓度和温度对乙醇转化率检验结果如表3所示。结果表明，乙醇浓度与温度均对乙醇转化率有较大的影响，而二者的交互作用对乙醇转化率的影响不显著。

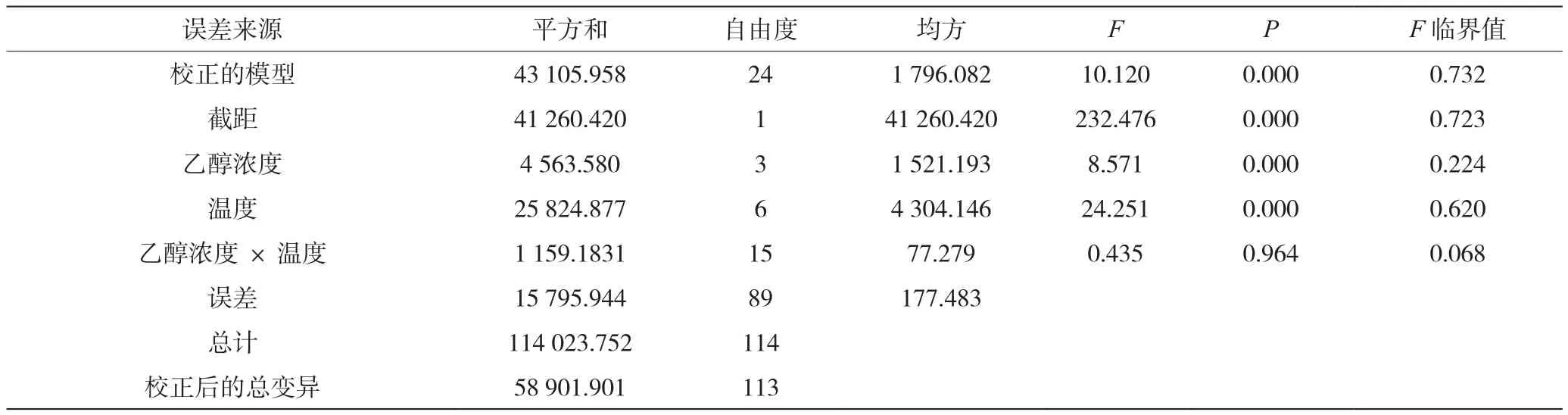
表3 温度和乙醇浓度对乙醇转化率的影响

2.3 多因素方差分析

利用SPSS 2.6进行数据分析，可以在双因素方差分析的基础上添加更多的因素来研究其对因变量的影响。催化剂组合中含有Co负载量、乙醇浓度及Co/SiO2和HAP配料比这几个要素，各要素检验结果如表4所示。可以发现乙醇浓度与Co负载量×乙醇浓度的P＜0.05，因此可以判定乙醇的浓度在催化剂组合中起到较为关键的作用。

表4 Co负载量、乙醇浓度及Co/SiO2和HAP配料比对乙醇转化率的影响

2.4 非线性回归模型

根据前述实验结果，确定乙醇浓度和温度为C4烯烃收率的约束因素，因此进行非线性回归近似模拟两种因素对C4烯烃收率的影响。

非线性回归模型表达式为：

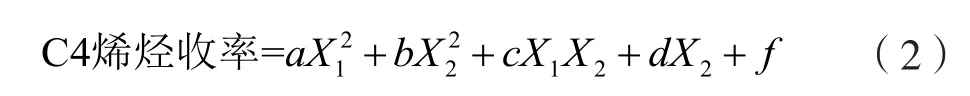
式中：X1为温度，X2为乙醇浓度，a、b、c、d、e、f为模型表达式的系数。

此方法是不断地将“参数估计值”代入“损失函数”求解，而损失函数采用的是“残差平方和”最小值。在迭代后，残差平方和达到最小值，且最小值为493.584，此时找到最优解，迭代终止，得到：a=0.001，b=-84 957.289，c=0.027，d=101 941.711，e=-0.614，f=-22 859.085。模型表达式为：C4烯烃收率=0.001X12-84 957.289X22+0.027X1X2+101 941.71X2-0.614X1-22 859.085。

将表达式输入MATLAB进行三维绘图，求解温度-乙醇浓度约束下C4烯烃收率最高点，如图2所示。结果表明，当温度为370 ℃，乙醇浓度为0.61 mL/min时，C4烯烃收率最大。

图2 温度-乙醇浓度-C4烯烃收率三维图

3 结论

本文研究了催化剂组合、温度对C4烯烃收率的影响。结果表明：乙醇转化率、C4烯烃选择性与温度有很强的线性正相关性，350 ℃时，乙醇转化率与时间表现出很强的线性负相关，C4烯烃选择性与时间不具有相关性；多因素方差分析发现乙醇转化率和C4烯烃选择性温度和乙醇浓度密切相关；非线性回归模型表达式为C4烯烃收率=0.001X12-84 957.289X22+0.027X1X2+101 941.71X2-0.614X1-22 859.085（X1为温度，X2为乙醇浓度）；利用MATLAB得出当温度为370 ℃，乙醇浓度为0.61 mL/min时，C4烯烃收率最大。