新型推力可控垂直发射装置及其内弹道规律

贾启明， 姜毅， 杨莹， 赵子熹， 王志浩

(北京理工大学 宇航学院， 北京 100081)

0 引言

当前，舰载垂直发射装置主要有两种：共用排焰道式和同心筒式。共用排焰道式垂直发射装置简化了燃气排导系统，提高了发射效率，但存在导弹发射时相邻导弹意外点火的问题；同心筒式垂直发射装置通过共轴内外筒和能够实现燃气转向的半球形端盖结构排导燃气，避免了相邻导弹意外点火的问题，且同心筒式垂直发射装置具有发射成本低、组装简单、发射模块可互换、通用性强等特点，优势明显，已经成为各国研究人员研究的重点。随着舰载武器的进一步发展，对发射装置的通用化提出更高的要求，在导弹和发射装置主体结构不变的情况下，通过简单的结构调节发射装置推力，将大幅提升发射装置的通用化水平。

对于同心筒式发射装置，内外筒间隙是影响流场的关键结构参数。针对内外筒间隙对于同心筒式发射装置内弹道的影响，袁绪龙等进行了定性的研究，对于同心筒水下发射装置，在同心筒筒口和筒底设置不同面积的节流环，可以调节导弹的出筒速度和发射最大过载。苗佩云等发现随着内外筒间隙的增大，在一定范围内，发射筒底最大压强会减小，之后再继续增大内外筒间隙，对流场的影响不明显。于勇等通过数值仿真发现，内外筒间缝隙的减小，发动机的激波位置从发动机外逐渐移动发动机内部，弹底所受的附加弹射力逐渐提高。郑榆淇等对异形同心筒进行研究，同心筒发射时的燃气排导间隙的减小，会增强发射筒内压强；马艳丽等对同心筒发射过程燃气射流进行研究，内外筒间距增大后，内筒中的温度先降低后增大，后盖处的压强随之逐渐降低，筒内的压力减小。此外，内外筒间隙对同心筒装置排导及热环境都有影响。傅德彬等、刘琦等研究发现，内外筒间隙对燃气排导效果有着直接影响，选择合适的内外筒间隙，可以使大部分燃气经发射筒底部导流进入内外筒间隙。于勇等通过将内外筒间隙设置成先收缩后扩张的变截面来加速燃气，降低同心筒底部的温度。

综上所述，改变同心筒内外筒间隙，将影响燃气出口面积，改变同心筒式发射装置内部流场，从而影响导弹受力。作为自力发射装置，同心筒装置在发射导弹的过程中会导致燃气烧蚀导弹表面；且由于其内外筒为共轴圆柱结构，即使导弹周向与内筒完全贴近，外筒与发射单元相切，也不可避免的造成矩形舰面发射单元有效空间的浪费，限制发射装置使用的导弹尺寸。为了实现舰载垂直发射装置推力可控，提高舰面发射单元空间利用率，本文在同心筒式发射装置的基础上，提出了一种新型的“类同心筒”弹射装置——推力可控垂直发射装置，如图 1所示，发射装置由燃气发生器、导流锥、发射筒和4个排焰道组成。发射导弹时，燃气从燃气发生器流出进入低压室，短时间内高温高压燃气聚集在低压室内，低压室内压强升高，高压燃气从周围4个排焰道流出，同时，高压燃气对导弹做功，推动导弹弹射出筒。根据不同的发射需求，调整4个排焰道出口附近管道面积将影响发射过程中低压室压强，进而实现控制导弹推力的目的。

图1 推力可控垂直发射装置Fig.1 Controllable thrust vertical launcher

针对本文提出的新型推力可控舰载垂直发射装置，首先从弹射内弹道理论出发，讨论低压室燃气出口面积变化对发射装置的推力的影响；再通过计算流体力学的方法对零维内弹道模型参数进行校验；通过零维内弹道模型对不同低压室燃气出口面积进行计算，将导弹弹射过程中的关键参数(弹射最大加速度，出筒速度，出筒时间)与低压室燃气出口面积进行多项式拟合；之后对5组不同排焰道出口面积弹射过程进行数值仿真，对拟合曲线预测结果进行验证，并讨论了不同燃气出口面积对发射过程中流场的影响。

1 计算方法

1.1 零维内弹道模型

在工程计算中，经常使用零维内弹道模型对发射装置内弹道性能进行初步估算。

零维内弹道假设：由于喷管中气流流动速度远高于高压室中气流流动速度，所以认为在高压室内燃气无流动，均一的压强、密度、温度代表高压室各处相应的物理量，即不考虑高压室压强等沿空间的分布，只考虑其随时间的变化规律。同样，由于在弹射器内导弹运动速度较低，燃气流动速度也很低，故不考虑燃气在低压室内的流动，即不考虑低压室压强在空间上的分布。

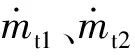
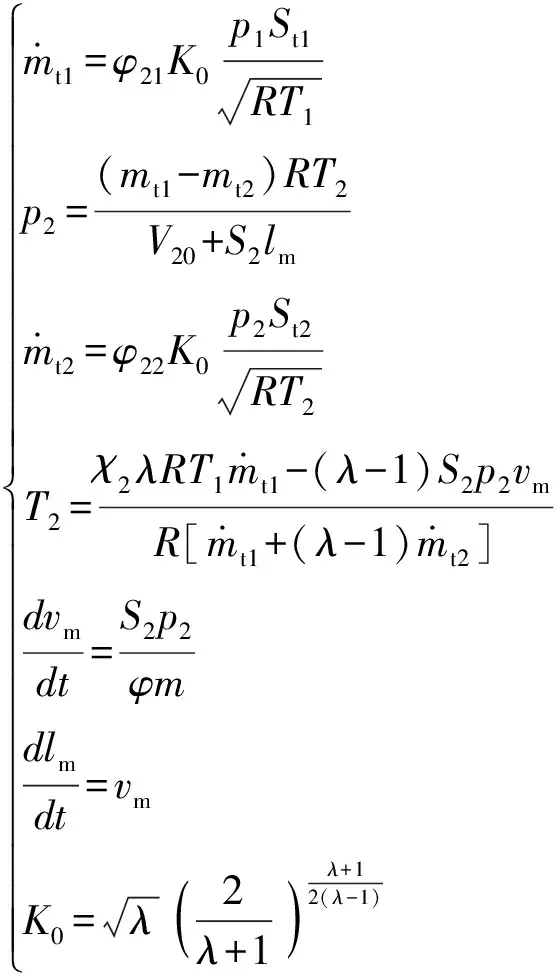
(1)

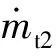
1.2 三维内弹道模型

由于零维内弹道是基于高低压室压强等平均假设展开，且未考虑发射装置几何特性对低压室流场的影响，因此，还需要引入气动模型建立三维内弹道模型对零维内弹道结果进行验证。三维内弹道模型一般借助计算流体力学(CFD)的方法，结合发射装置三维几何模型，进一步揭示低压室燃气出口面积变化对推力可控发射装置流场及内弹道的影响。

121 控制方程

发射装置发动机点火时，高压室压强较大，高压燃气经过喷管后变成超声速燃气，将其按照可压缩气体处理。可压缩气体控制方程组如下：

质量守恒方程：

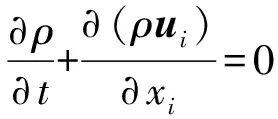
(2)

动量守恒方程：

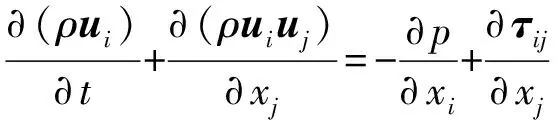
(3)

能量守恒方程：

(4)

式中：为时间；为密度；、为、方向速度分量；为应力张量；是内能与动能之和，为流体微团的总能量；为热通量。

122 湍流模型

在标准-模型的基础上，Realizable-模型提出了一种新的耗散模型方程以及一个新的包含变量的涡旋粘度公式，能更真实地反映旋转流动、强逆压梯度的边界层流动以及流动分离等现象。Realizable-湍流模型中，关于湍动能和耗散率的输运方程为

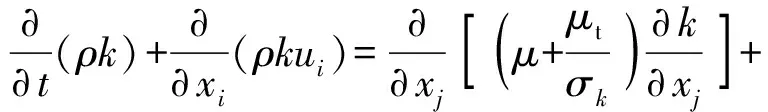
(5)

(6)

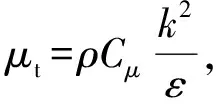
123 湍流模型验证

本文的研究内容是：高温高压燃气从燃气发生器流出后冲击导流锥，在低压室聚集后推动导弹运动，是典型的冲击射流问题。因此选用燃气冲击斜平板验证Realizable-湍流模型对此类问题的适用性。

根据文献[14-16]试验建立模型，对非设计度为2，平板倾斜角度为55°，喷管出口中心到平板的距离为喷管出口直径的2倍的燃气冲击斜平板进行仿真。图2为试验纹影图与仿真流场密度云图对比，仿真结果可以准确捕捉射流的激波结构，仿真结果中最值位置与试验结果基本一致。

图2 试验结果与仿真结果对比Fig.2 Comparison of test data and simulation results

平板上压强分布对比如图3所示，其中横坐标为平板各点到射流轴线距离与喷管出口半径之比，距离喷管较近的方向为正，纵坐标为平板上各点压强与总压之比。仿真数据与试验数据趋势一致，准确计算出了压强的两个峰值点，且仿真数据与试验数据误差较小。因此采用Realizable-湍流模型对燃气冲击流场进行数值计算是合理的。

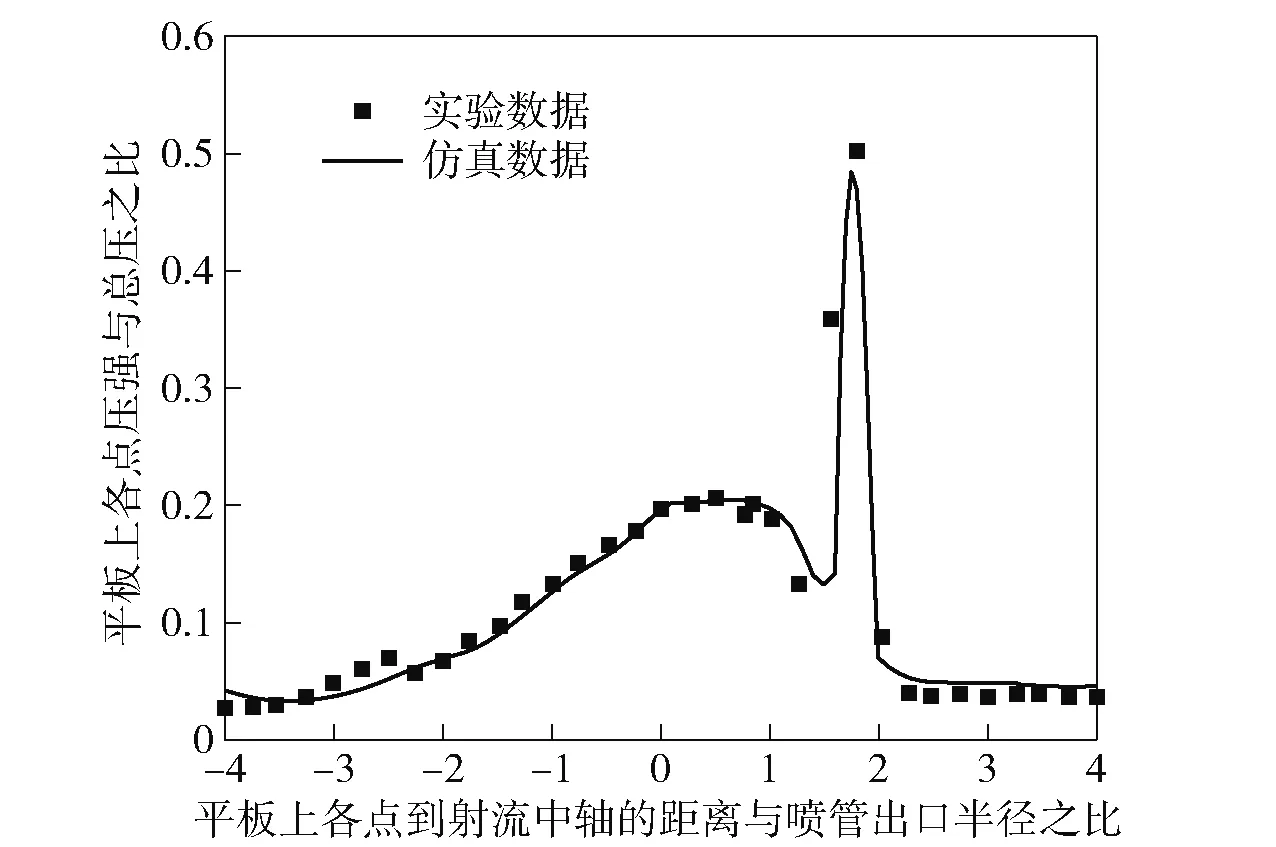
图3 平板上压强分布Fig.3 Pressure distribution on the plate

124 三维内弹道计算方法验证

推力可控发射装置的关键是通过控制燃气出口面积，来控制弹射过程中低压室压强，为验证三维内弹道计算方法准确性，采用低压室有燃气出口的筒式弹射试验与仿真进行对比。试验装置示意图如图4、图5所示，发射时燃气从高压室流出，之后推动隔离板与弹运动，隔离板与发射筒和导轨之间存在间隙，燃气可以从间隙中流出。

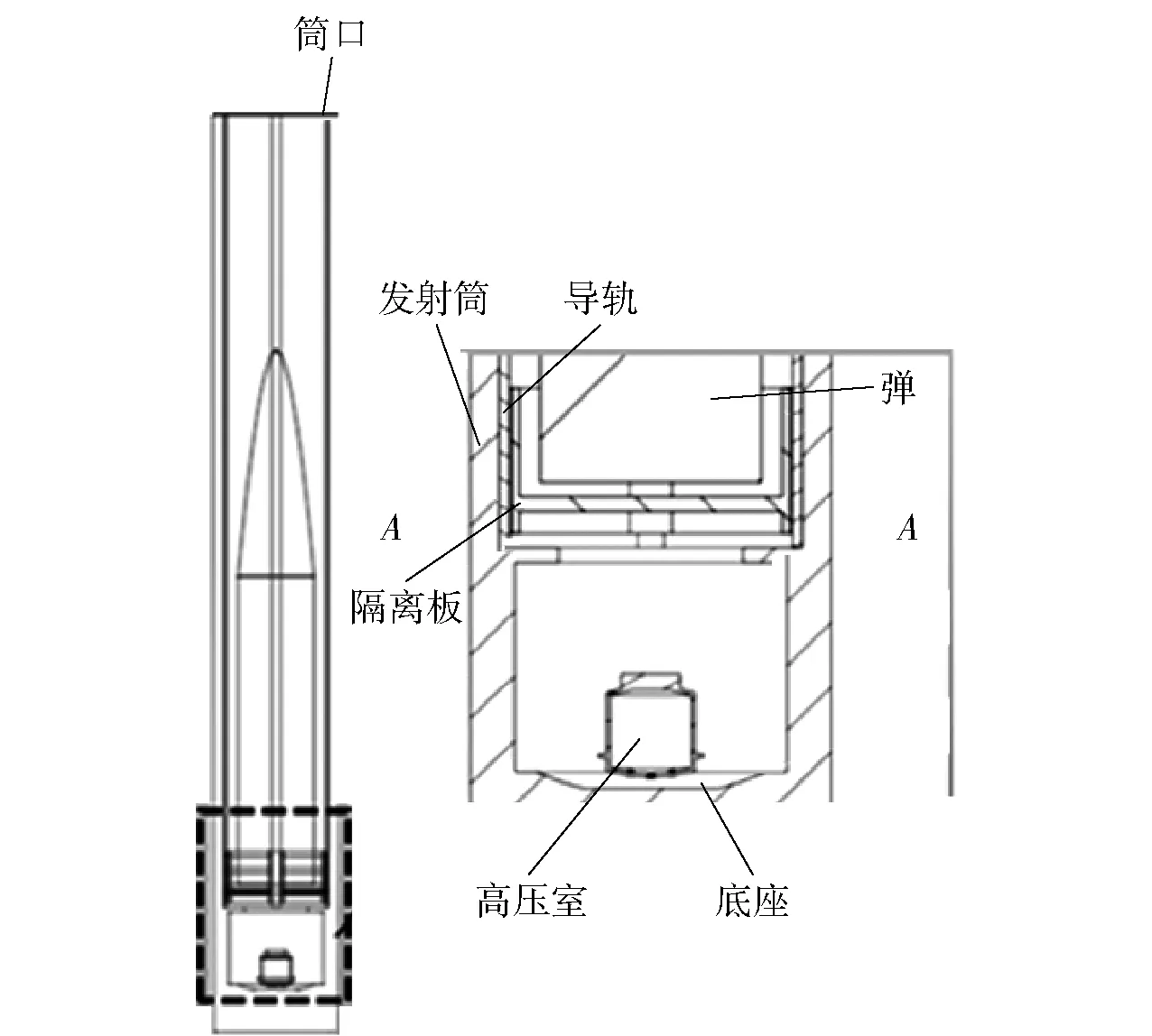
图4 试验装置示意图Fig.4 Schematic diagram of experimental device

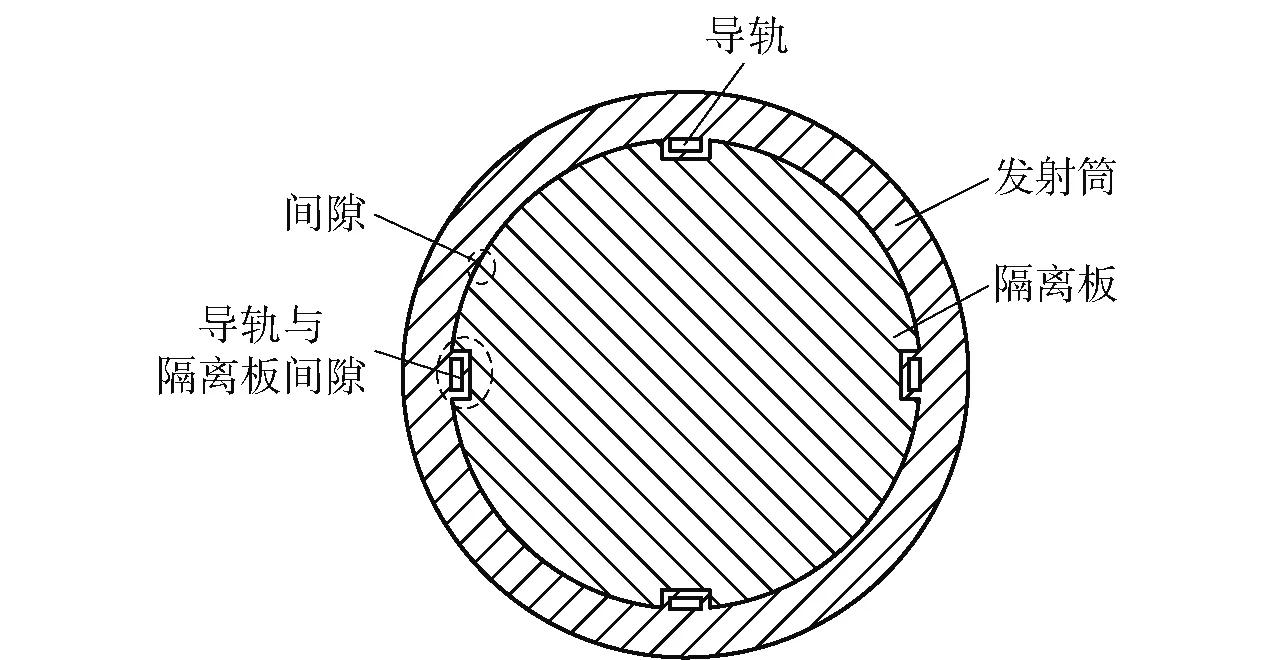
图5 A-A截面图Fig.5 Sectional view A-A

根据试验模型建立流场模型，采用试验测得的高压室压强时间作为燃气发生器的输入，无量纲处理后的高压室压强曲线如图6所示，对弹射过程进行仿真。将试验与仿真低压室压强进行对比，如图7所示，为试验参考压强，仿真结果与试验结果的低压室压强趋势基本一致，其中仿真结果的第1个低压室压强峰值为0610，试验结果为0624；仿真结果的第2个低压室压强峰值为0835，试验结果为0792；第1个压强峰值相差较小，第2个压强峰值相差较大，但误差在55内，说明三维内弹道计算方法能够较为准确的模拟低压室存在燃气出口条件下的弹射过程。

图6 试验得到的高压室压强曲线Fig.6 Pressure curve of the high-pressure chamber obtained from the experiment

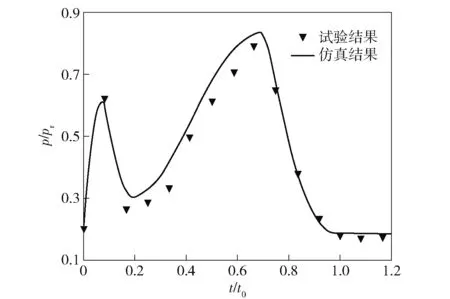
图7 低压室压强曲线对比Fig.7 Comparison of pressure curves in low pressure chambers

2 模型校验

2.1 网格模型及边界条件

针对图1中推力可控垂直发射装置几何模型，构建流场域，采用结构网格与非结构网格混合的方式划分流场域，网格模型如图8所示，采用域动分层法进行网格实时更新。

图8 网格模型Fig.8 Grid model

计算流场边界条件设置如图9所示，设置发动机喷管入口为压力入口。采用有限体积法离散流场的控制方程，选用Realizable-湍流模型，发动机内工质视为混合燃气，壁面附近设置为标准壁面函数，采用基于压力基的PISO(pressure implicit with split operators) 算法进行非定常迭代计算。

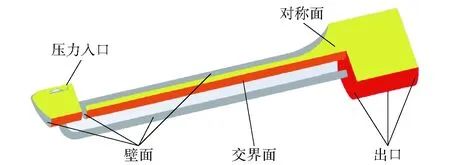
图9 边界条件设置Fig.9 Boundary condition setting

2.2 零维内弹道模型参数校验

高压室压强时间曲线如图10所示，纵坐标压强进行无量纲处理，保持排焰道全部开启，即燃气出口面积为0.048 m。利用计算流体力学软件，通过用户自定义函数将图10中压强曲线设置为压力入口压强，设置发动机总温1 400 K，环境压强101 325 Pa，温度300 K，对图8中的网格进行流场仿真计算，得到两种方法弹射过程中导弹加速度、速度与行程。

图10 高压室压强时间曲线Fig.10 Pressure-time curve of the high pressure chamber

图11为导弹弹射过程中流场温度云图，高温燃气从燃气发生器流出后，沿导流锥向四周流动，在低压室内聚集，低压室温度逐渐升高到总温温度；发射初期，高压室压强较小，导弹受到的压差力小于重力，随着高压室压强增大，低压室压强增大，低压室内的高压燃气推动导弹运动出筒，同时通过排焰道流出。

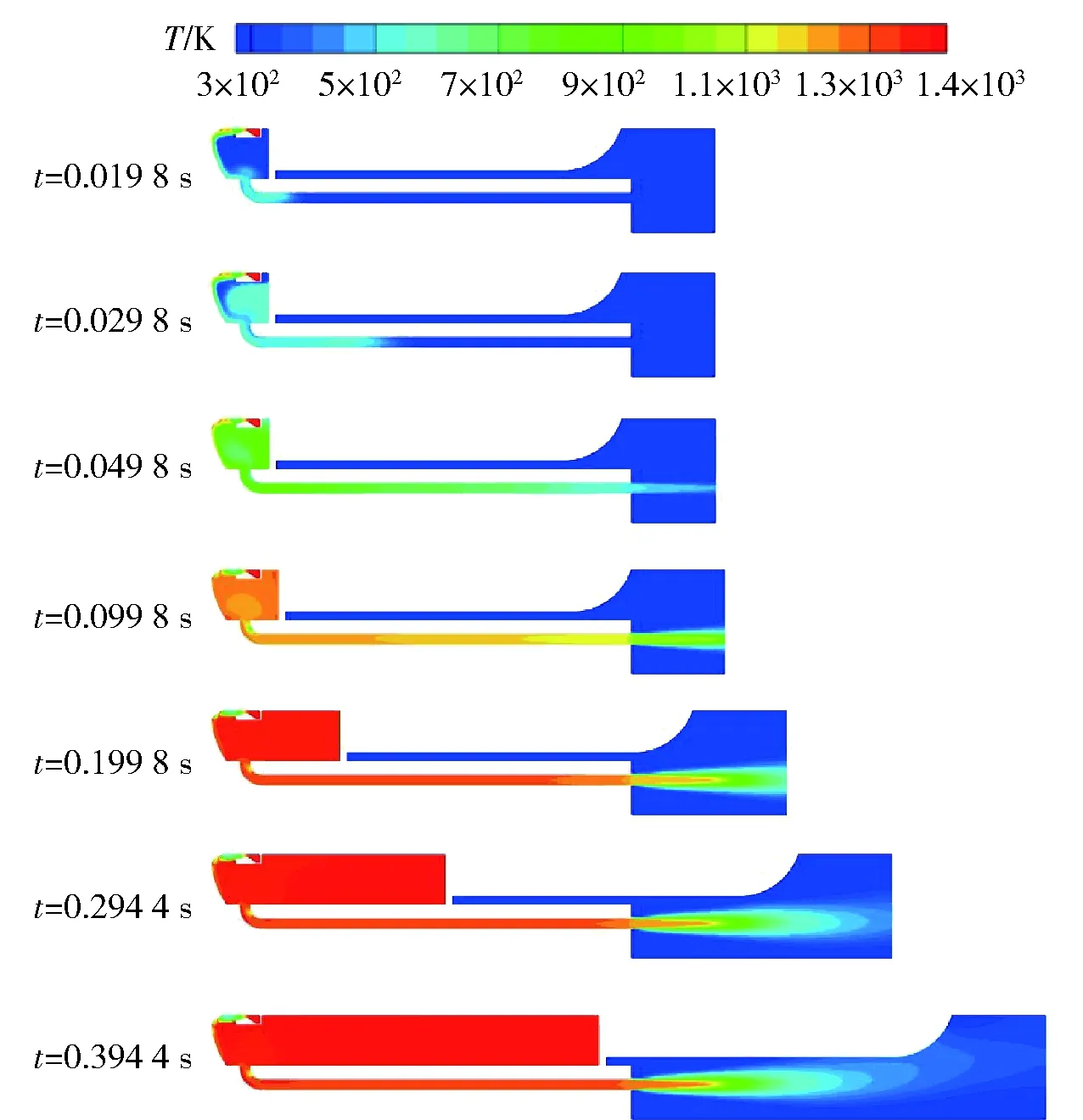
图11 弹射过程中温度云图Fig.11 Temperature cloud map during ejection

根据推力可控发射装置几何模型设置(1)式中的常量，采用四阶Runge-Kutta 法对弹射内弹道方程组进行求解。利用CFD仿真计算得到的弹射过程中的加速度、速度和位移，对零维内弹道模型中的次要功系数，高压室喷管流量修正系数，低压室出口流量修正系数与散热修正系数进行修正。导弹弹射过程CFD与零维内弹道结果如图12所示。零维内弹道的计算结果与CFD结果的弹射过程加速度、速度与位移曲线重合较好，两者误差较小——其中零维内弹道的最大加速度、出筒速度和出筒时间相对于CFD误差为3.17%、0.57%、1.16%。

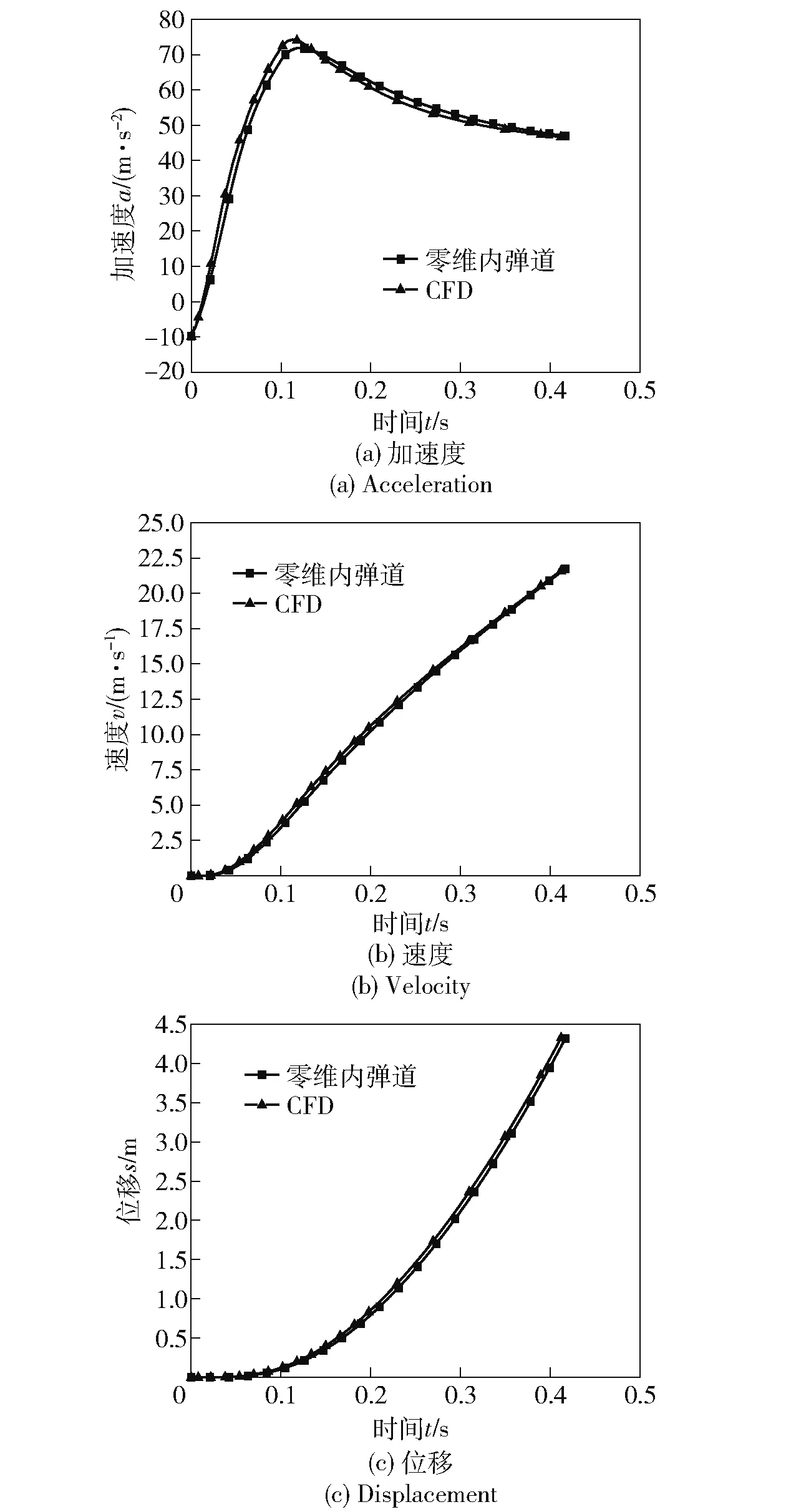
图12 弹射过程CFD与零维内弹道结果对比Fig.12 Comparison of CFD during ejection and zero-dimensional interior ballistic results

3 推力调节规律及验证

3.1 推力调节规律研究

保持零维内弹道模型其他参数不变，计算低压室燃气出口面积从0 m到0.048 m变化过程中推力可控发射装置内弹道性能变化，图13为低压室燃气出口面积为0 m、0.01 m、0.02 m、0.03 m、0.04 m、0.048 m时弹射过程导弹加速度时间曲线、速度时间曲线与位移时间曲线。在导弹质量不变的情况下，随着低压室燃气出口面积的变化，导弹加速度变化趋势相同——先增大到最大加速度之后逐渐减小；导弹达到最大加速度的时间没有明显变化，都在=0.12 s附近，这是由于高压室压强在0.1 s之后变化放缓，低压室压强在0.1 s之后达到最大值；而随着低压室燃气出口面积的减小，导弹最大加速度明显增大，从71.88 m/s增大到166.46 m/s；导弹的出筒时间从0.416 s减小到0.295 s，导弹的出筒速度从21.728 m/s增大到30.855 m/s。

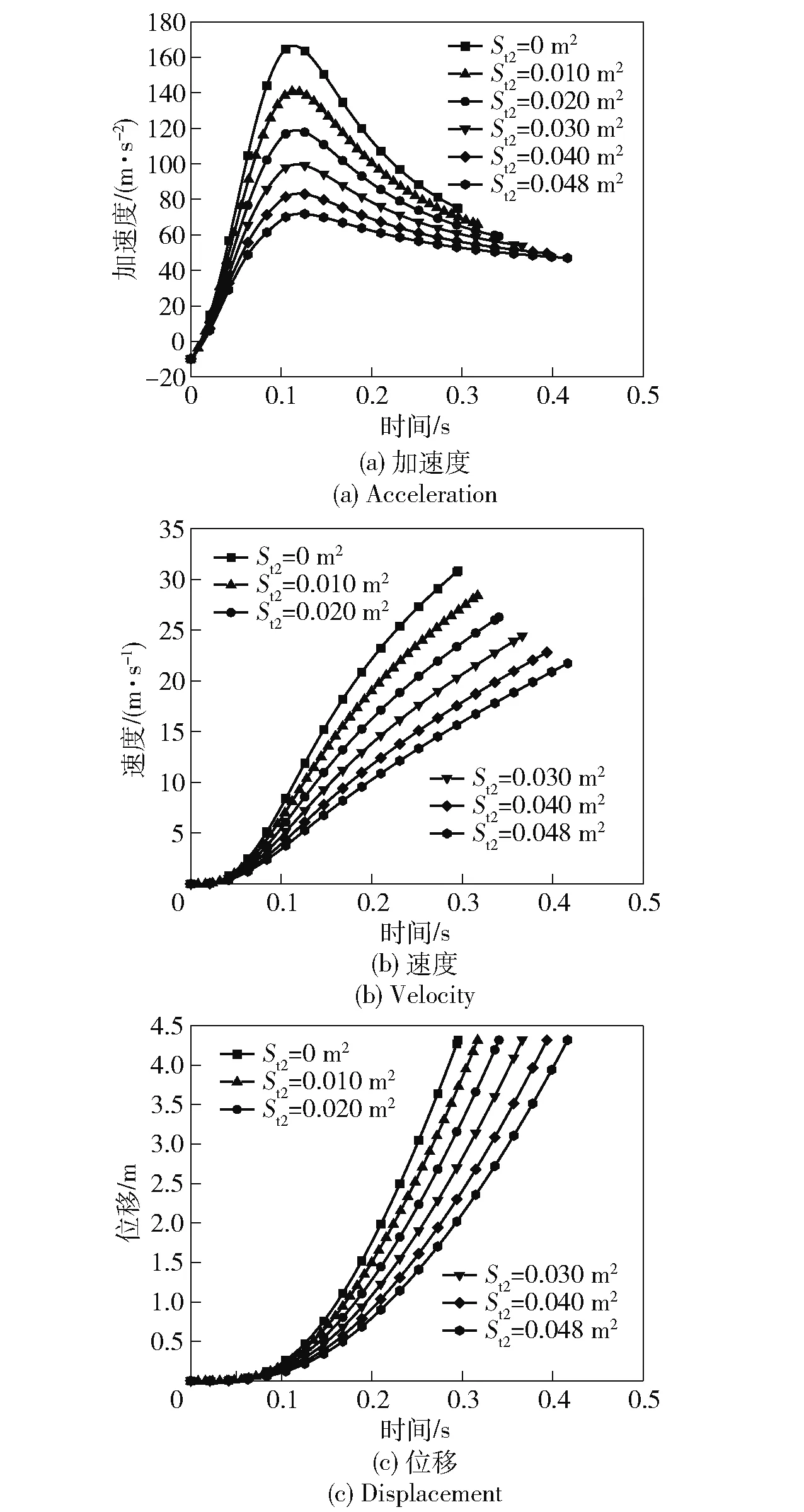
图13 不同St2对应的弹射过程导弹运动曲线Fig.13 The movement curve of the missile in the ejection process corresponding to different St2

进一步缩小间隔，针对不同低压室燃气出口面积进行零维内弹道计算，表1列出了低压室燃气出口面积0 m到0048 m之间弹射内弹道关键参数——导弹最大加速度、出筒速度与出筒时间，随着低压室燃气出口面积增大，导弹最大加速与出筒速度逐渐减小，导弹出筒时间逐渐增大。

运用多项式拟合方法对表1中的数据进行拟合，得到与、、1阶多项式、2阶多项式、3阶多项式拟合结果，如图 14所示，3种拟合结果都在数据点周围，其中2阶多项式与3阶多项式拟合结果基本贯穿每一个数据点。

表1 不同St2对应弹射内弹道参数

多项式拟合结果吻合度如表2所示。随着阶数的增加，与、、多项式拟合的和方差与均方根逐渐趋近与0，说明3阶多项式拟合更好；决定系数与修正决定系数都接近1，其中2阶多项式和3阶多项式决定系数都等于1，说明对、、的解释能力较强，多项式模型对于数据拟合的结果较好。3阶多项式拟合结果如下，其中∈[0,0048]。

(7)

(8)

(9)

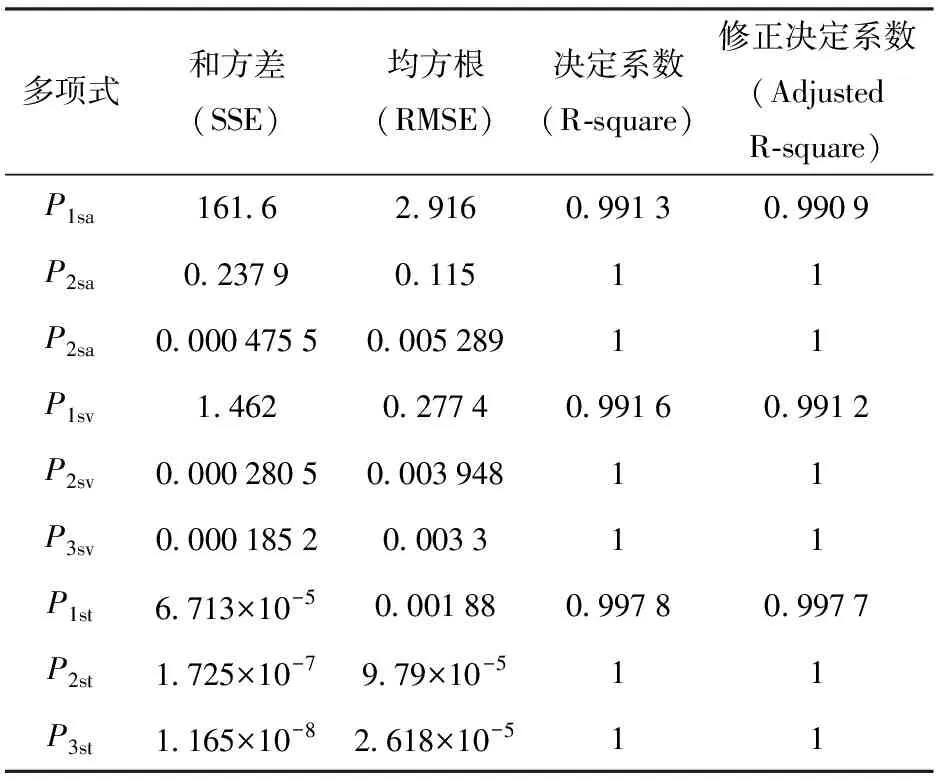
表2 多项式拟合吻合度

3.2 推力调节规律验证

通过CFD的方法对(7)式～(9)式进行验证，更改排焰道在出口处的面积如图15所示，设置5种不同的燃气出口面积分别为工况1(0.008 m)、工况2(0.016 m)、工况3(0.032 m)、工况4(0.04 m)、工况5(0.048 m)，进行仿真计算。

图14 多项式拟合结果Fig.14 Polynomial fitting results

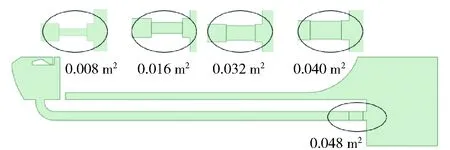
图15 排焰道变截面示意图Fig.15 Schematic diagram of the variable cross-section of the exhaust duct

图16为通过CFD仿真得到的不同燃气出口面积对应的导弹运动曲线。由图16可见：在=0-0.03 s时，导弹速度较小，导弹基本没有运动，这段时间内燃气刚充满低压室和排焰道，燃气出口面积变化对低压室压强的影响较小，所以5种出口面积对应导弹加速度基本重合；在=0.03 s之后，随着高压室压强的进一步增加，不同的燃气出口面积，导致燃气在出口处不同程度的壅塞，影响低压室压强，导致不同工况低压室压强发生变化，进而影响导弹加速度，导弹加速度、速度、位移变化趋势与图 13基本保持一致，且CFD仿真计算得到导弹达到最大加速度时间也在=0.12 s附近。

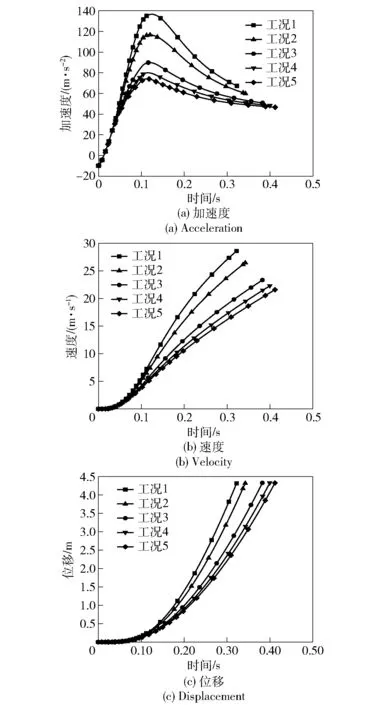
图16 导弹运动曲线Fig.16 Missile movement curve

在发射过程中，导弹沿发射方向受到压差力和重力作用，导弹达到最大加速度时，压差力最大。由图16可知，5种工况在=0.12 s附近，导弹达到最大加速度，取五种工况=0.12 s时压强云图如图17所示，工况1至工况5低压室与排焰道内压强逐渐减小，表明燃气出口面积的变化对低压室压强有明显的影响。

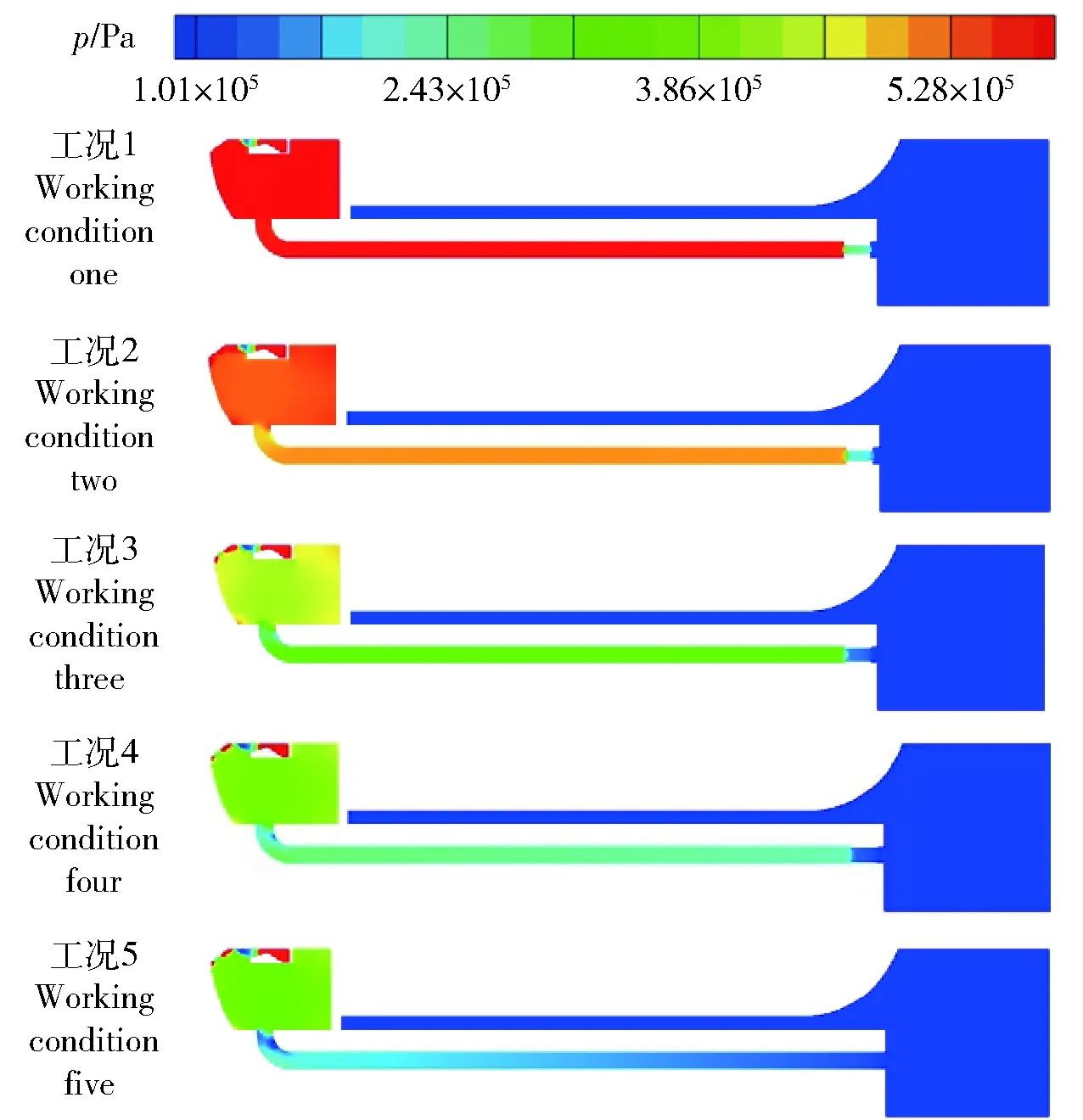
图17 t=0. 12 s时压强云图Fig.17 Pressure cloud map at t=0.12 s

图18为导弹出筒前温度云图，随着出口面积变小，发射筒内温度有一定程度的减小；高温燃气经过变截面出口后从排焰道排出，在流场外域扩散后，随着出口面积变小，燃气在外域中扩散角度减小，燃气出口温度减小。根据文献[2]，燃气出口面积减小，燃气出口速度增大，燃气动能增大，而燃气的总能量不变，则燃气内能减小，温度降低。

图18 导弹出筒时温度云图Fig.18 Temperature cloud map when the missile is about to exit the canister

表3为5种工况对应(7)式～(9)式预测结果及相对于CFD仿真结果的误差，其中出筒速度和出筒时间的相对误差较小，都在4%以内，最大加速度相对误差较大，在8%以内。因此，可以认为在一定精度下，基于零维内弹道结果拟合得到的导弹出筒时间、出筒速度、最大加速度与低压室燃气出口面积的关系式具有较高的精度。在已知的燃气发生器压强曲线(见图10)及推力可控发射装置几何(见图1)的前提下，可以通过(7)式～(9)式，得到低压室燃气出口面积对应的弹射最大加速度、出筒速度和出筒时间，进行初步的发射安全性校核；在已知导弹弹射最大过载的前提下，可以通过(7)式～(9)式反推得到低压室燃气出口面积，以满足发射需求。

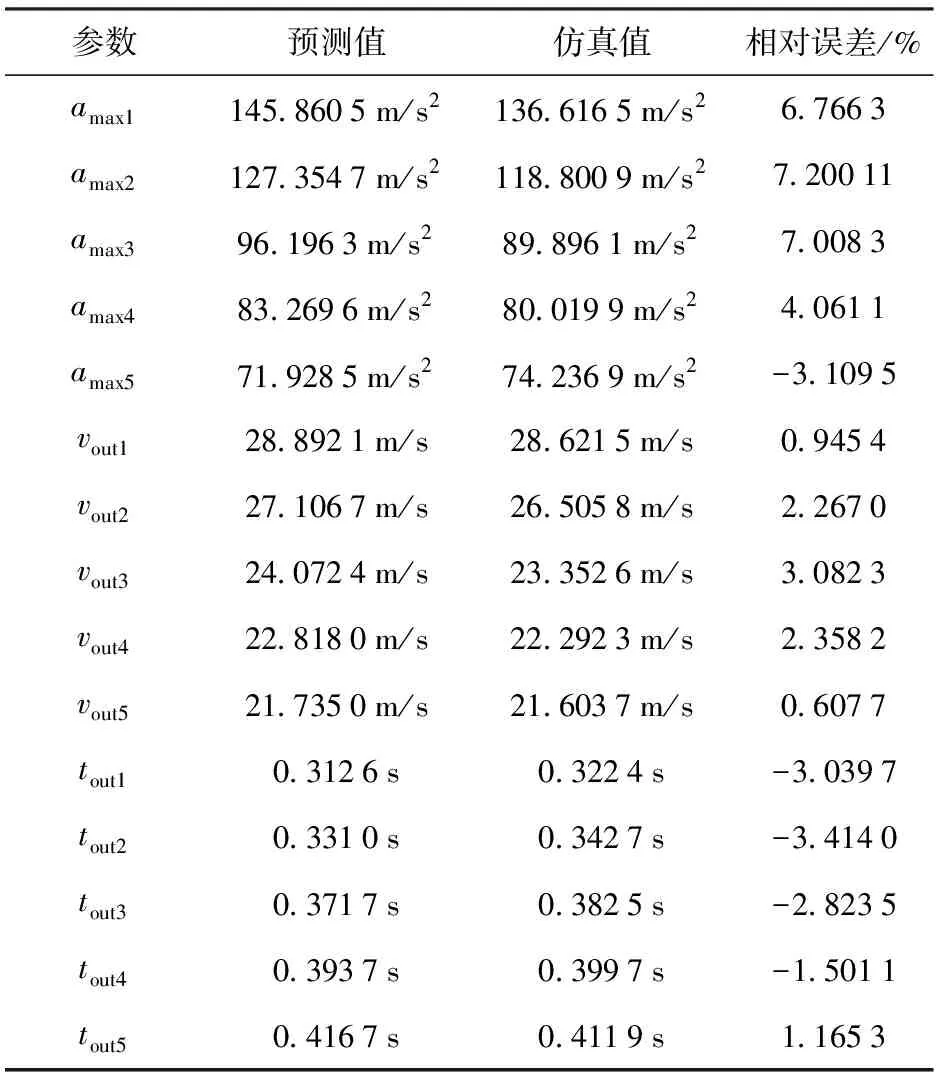
表3 弹射内弹道参数预测值及相对误差

4 结论

为提高发射装置的通用性，本文提出了一种新型“类同心筒”弹射装置——推力可控垂直发射装置。基于弹射内弹道理论，讨论了低压室燃气出口面积变化对发射装置的推力的影响，利用计算流体力学方法进行了三维内弹道仿真，对零维内弹道模型参数进行校验，对不同低压室燃气出口面积进行计算；根据零维内弹道结果，对低压室燃气出口面积与弹射最大加速度、出筒速度、出筒时间进行多项式拟合，并通过三维内弹道仿真对拟合结果进行了验证。得到主要结论如下：

1)通过零维内弹道计算和三维内弹道数值仿真两方面，论证了通过改变低压室燃气出口面积控制发射装置推力是可行的。

2)导弹出筒时间、出筒速度、最大加速度随低压室燃气出口面积近似线性变化——低压室燃气出口面积减小，导弹最大加速度增大，出筒速度增大，出筒时间减小。

3)通过多项式拟合得到了低压室燃气出口面积与弹射最大加速度、出筒速度、出筒时间的关系式，利用数值仿真验证了拟合关系式的精度，其中拟合关系式的弹射最大加速度误差在8%以内，出筒速度与出筒时间误差在4%以内，为推力可控发射装置设计了理论参考依据，为工程设计提供设计思路。

[1] 边金尧, 徐松林, 钱海鹰. 同心发射筒研究现状[J]. 舰船科学技术, 2012, 34(11):1-5,51.

BIAN J Y, XU S L, QIAN H Y. Research progress of concentric launching canister[J]. Ship Science and Technology, 2012, 34(11): 1-5,51. (in Chinese)

[2] 于勇, 母云涛. 新型变截面同心筒发射装置及其热环境气动原理研究[J]. 宇航学报, 2013, 34(9): 1281-1287.

YU Y，MU Y T. Configuration and gas dynamics analysis for a new variable cross-section concentric canister launcher [J]. Journal of Astronautics, 2013, 34(9): 1281-1287. (in Chinese)

[3] 苗佩云, 袁曾凤. 同心筒式发射时筒内流场机理及内外筒间隙的影响[J]. 战术导弹技术, 2006, 29(1): 8-13.

MIAO P Y, YUAN Z F. The effect of flow mechanism and annular sizes on concentric canister launcher[J]. Tactical Missile Technology January, 2006, 29(1): 8-13. (in Chinese)

[4] 袁绪龙, 王亚东, 刘维. 同心筒水下发射内弹道建模与仿真研究[J]. 弹道学报, 2013, 25(2): 48-53.

YUAN X L, WANG Y D, LIU W. Interior ballistic modeling and simulation of underwater launched missile using concentric canister launcher [J]. Journal of Ballistics, 2013, 25(2): 48-53. (in Chinese)

[5] 于勇, 母云涛. 同心筒式发射装置附加弹射力影响因素分析[J]. 航空动力学报, 2014, 29(4):980-986.

YU Y, MU Y T. Influential factors analysis to additional ejection force in concentric canister launcher [J]. Journal of Aerospace Power, 2014, 29(4): 980-986. (in Chinese)

[6] 郑榆淇,傅德彬,王新星,等. 异形截面同心筒燃气流动特性数值研究[J]. 固体火箭技术, 2016, 39(5): 729-734.

ZHENG Y Q, FU D B, WANG X X, et al. Numerical investigation of exhaust flows for missile launching in an irregular section concentric canister launcher [J]. Journal of Solid Rocket Technology, 2016, 39(5): 729-734. (in Chinese)

[7] 马艳丽, 姜毅, 王伟臣,等. 湿式独立自排导垂直发射技术研究[J]. 导弹与航天运载技术, 2011(2): 29-33,51.

MA Y L, JIANG Y, WANG W C, et al. Research on the wet-type concentric canister launcher [J]. Missiles and Space Vehicles, 2011(2): 29-33,51. (in Chinese)

[8] 马艳丽, 姜毅, 王伟臣,等. 同心筒发射过程燃气射流冲击效应研究[J]. 固体火箭技术, 2011, 34(2): 140-145.

MA Y L, JIANG Y, WANG W C, et al. Study on impact effect of combustion gas jet during concentric canister launching process [J]. Journal of Solid Rocket Technology, 2011, 34(2): 140-145. (in Chinese)

[9] 傅德彬, 姜毅, 陈建伟,等. 同心筒自力发射燃气排导优化设计[J]. 弹箭与制导学报, 2004, 24(3): 42-45.

FU D B, JIANG Y, CHEN J W, et al. Optimization design for concentric canister launcher combustion gas exhaust [J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2004, 24(3): 42-45. (in Chinese)

[10] 刘琦, 傅德彬, 姜毅,等. 同心筒发射装置燃气射流流场非定常数值模拟[J]. 弹箭与制导学报, 2004, 24(3): 161-163.

LIU Q, FU D B, JIANG Y, et al. Unsteady simulation of jet flow in concentric canister launcher [J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2004, 24(3): 161-163. (in Chinese)

[11] 谭大成. 弹射内弹道学[M]. 北京: 北京理工大学出版社, 2015:84-102．

TAN D C. Interior ballistics of catapults[M]. Beijing: Beijing Institute of Technology Press, 2015: 84-102. (in Chinese)

[12] 唐垚,姜毅,王成德,等. 多级活塞缸式燃气弹射内弹道的研究[J]. 固体火箭技术, 2018, 41(4): 524-531.

TANG Y, JIANG Y, WANG C D, et al. Research on the internal trajectory of multi-stage piston cylinder gas ejection [J]. Journal of Solid Rocket Technology, 2018, 41(4): 524-531. (in Chinese)

[13] SHIH T H, LIOU W W, SHABBIR A, et al. A new κ-ε eddy viscosity model for high reynolds number turbulent flows[J]. Computers Fluids, 1995, 24(3): 227-238.

[14] LAMONT P J. The impingement of underexpanded, axisymmetric jets on perpendicular and inclined flat plates[J]. Journal of Fluid Mechanics, 2006, 100(3): 471-511.

[15] CINNELLA P, TONG X L, WU J X, et al. Comprehensive numerical study of jet-flow impingement over flat plates[J]. Journal of Spacecraft & Rockets, 2002, 39(3): 357-366.

[16] 杨桦,姜毅,陶倩楠, 等.复燃现象对导流器排导流场影响数值分析[J].固体火箭技术,2020,43(3):393-399.

YANG H, JIANG Y, TAO Q N, et al. Numerical analysis of afterburning’s influence on division flow field with deflector [J]. Journal of Solid Rocket Technology, 2020, 43(3): 393-399. (in Chinese)

[17] 郝继光, 姜毅, 韩书永, 等. 一种新的动网格更新技术及其应用[J]. 弹道学报, 2007, 19(2): 88-92.

HAO J G, JIANG Y, HAN S Y, et al. A New dynamic mesh update method and its apllications [J]. Journal of Ballistics, 2007, 19(2): 88-92. (in Chinese)