一种基于遥测信息的外弹道择优方法

谢 超,顾青涛,龚 亮

(中国人民解放军32034部队,四川 成都 610500)

为了能够可靠跟踪飞行目标,航天靶场测控系统多采用光学、脉冲雷达、测速雷达和GNSS遥测等测控设备对目标进行测量。中心计算机系统综合这些测量信息进行外弹道解析,形成基于多种测量体制的大量弹道,并从中优选一条弹道用于目标态势显示、高精度测量设备引导、目标落点预报、地面安全控制等外围领域。这些都要求中心不断提升优选弹道的精度,因此,目前仅依靠人工优选的方式已经不能满足高自动化、高精度、高可靠性的要求。提高优选弹道的精度一般分2个步骤,分别为提高弹道自身精度和进行正确优选。提高弹道自身精度的方法是提高单信息源(如光学、雷达或GNSS等)弹道的精度或者进行多信息源弹道融合(如UKF滤波)。进行正确优选则要求选择的弹道结果符合目标实际飞行情况且精度最高。目前中心机系统主要依靠人工在光学、脉冲雷达、连续波雷达、GNSS差分等多种弹道间进行择优切换,在准确性、高效性和可靠性上都有所欠缺且无法参考遥测参数信息。遥测参数信息是目标内部正常工作的关键因素,同时这些遥测信息同外测弹道有着不可分割的联系。因此,建立遥测参数同外测弹道的关联模型,通过基于遥测信息的外弹道择优方法对中心外测弹道进行择优不仅能提高弹道择优的精度、效率和可靠性,而且能够为弹道择优提供第三方标准。本文依据空间坐标变换理论和经典动力学理论构建了遥测角度同外测速度、遥测视加速度同外测加速度的关联模型,提出了一种基于遥测信息的外弹道择优方法,为航天靶场实时弹道择优提供了新的手段,同时也可以提高外测弹道择优的效率和精度。

1 遥测角度同外测速度关联模型构建

由发射坐标系与弹体坐标系的转换关系及弹体坐标系与速度坐标系的转换关系可得发射坐标系同速度坐标系之间的转换矩阵。具体关系如下:

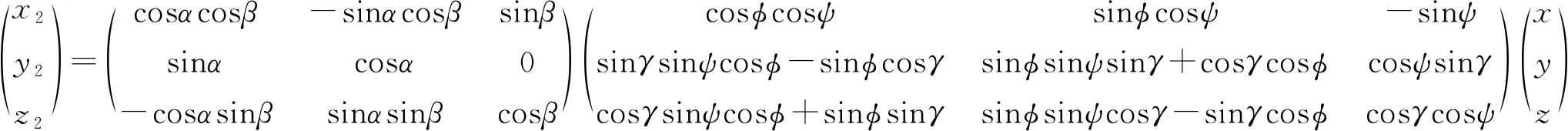
(1)

式中:,分别为攻角和侧滑角;,,分别为俯仰角、偏航角和滚动角。同时发射坐标系同速度坐标系的关系又可直接表示为

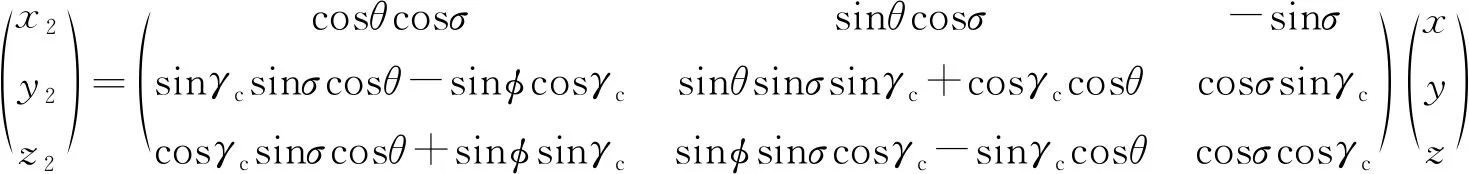
(2)

式中:,,分别为弹道倾角、弹道偏角和速度倾斜角。

联合式(1)和式(2),显然方程左边相等,则方程右边也相等。通过矩阵乘法原理可得式(1)右边两矩阵乘积结果,令乘积结果同式(2)右边矩阵的第一行第一列、第一行第二列、第一行第三列对应的位置的元素相等,可得如下方程:

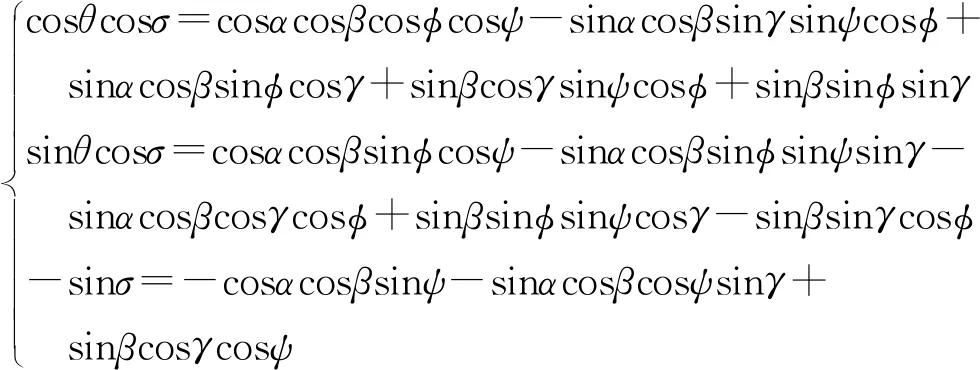
(3)

由于弹道倾角和弹道偏角可以通过外测速度分量进行求解,如图1所示为弹道倾角和弹道偏角与外测速度分量的关系图。

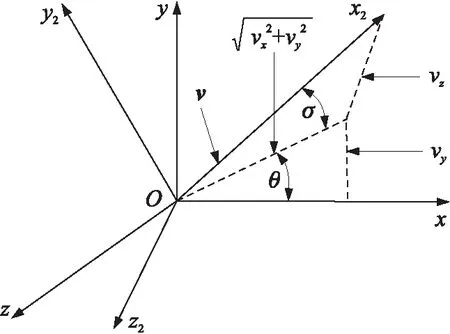
图1 弹道倾角和弹道偏角与外测速度分量关系图

如图1所示,为发射坐标系,其中坐标原点在发射点,轴在发射点水平面内指向发射瞄准方向,轴沿发射点的铅垂线向上,轴与轴、轴构成右手直角坐标系。为速度坐标系,轴与箭体质心的速度矢量重合,轴在箭体对称面内且与轴垂直,轴与轴、轴构成右手直角坐标系。弹道倾角和弹道偏角体现了发射坐标系和速度坐标系之间的关系。弹道倾角为速度矢量在平面内的投影与轴间的夹角,当投影在轴之上时为正,反之为负;弹道偏角是速度矢量与平面之间的夹角。当速度矢量在平面左边时为正,反之为负。,,为速度矢量在发射坐标系中的投影,则弹道倾角、弹道偏角可通过下式求解:

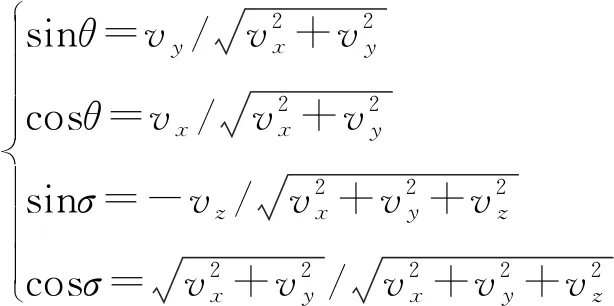
(4)

将式(4)代入式(3)得:

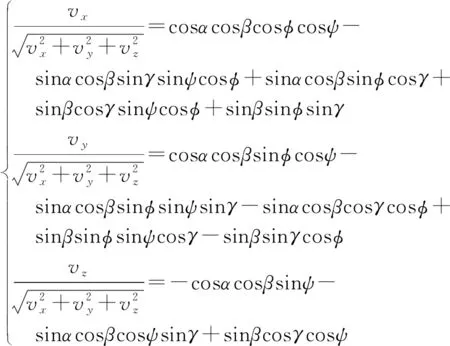
(5)

式(5)即为遥测角度同外测速度之间的关联模型。其中方程右边为遥测角度函数,包括俯仰角、姿态角、滚动角、攻角和侧滑角,可通过遥测参数实时测量结果得到;方程左边为外测速度在轴、轴、轴的单位方向向量。

2 遥测视加速度同外测加速度关联模型构建

遥测视加速度与外测加速度之间存在如下关系:

=+

(6)

式中:为外测加速度,为遥测视加速度,为重力加速度。

外测加速度一般是相对于发射坐标系,因此需要求解视加速度和重力加速度在发射坐标系中的分量。先求解重力加速度分量,由于重力加速度在轴向和地球自转方向的分量可通过下式求解:

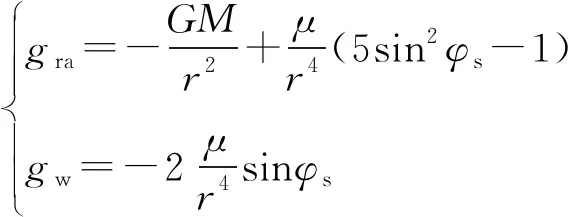
(7)

式中:地心引力常数=398×10m/s;地球椭球体扁率常数=2633×10m/s;,分别为空间目标点的地心纬度和地心矢径。

则重力加速度在发射坐标系的分量为

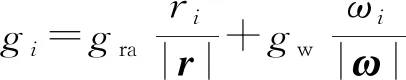
(8)

式中:为重力加速度在发射坐标系的分量;,分别为地心矢径、地球自转角速度在发射坐标系中的分量;||,||分别为地心矢径和地球自转角速度的向量长度;代表,,。

其次求解视加速度在发射坐标系中的分量。视加速度根据导航方式的不同可以分为惯性视加速度和捷联视加速度,两者求解方法不同。

①惯性视加速度在发射坐标系的分量为

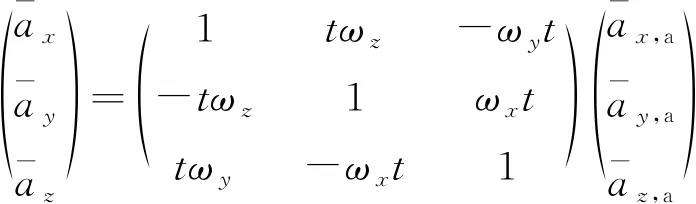
(9)

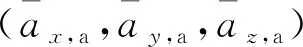
②捷联视加速度在发射坐标系中的分量为

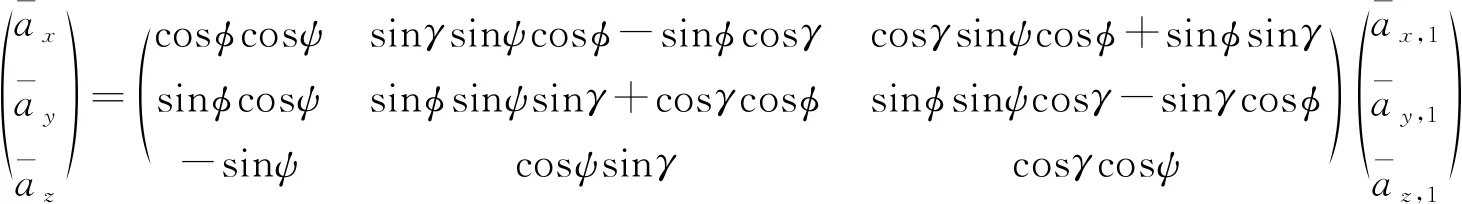
(10)

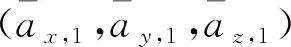
将式(8)、式(9)代入式(6)可得惯性视加速度同外测加速度的关联模型;将式(8)、式(10)代入式(6)可得捷联视加速度同外测加速度的关联模型。式中遥测视加速度可通过遥测参数获得,外测加速度可通过外测弹道测量结果得到。

3 基于遥测信息的弹道择优方法

以第1节、第2节中遥测信息与外弹道关联模型为基础,提出基于遥测信息的外弹道择优方法。择优步骤如下:

①以式(5)为基础,计算方程右边遥测角度函数数值同方程左边所有外测弹道速度方向余弦数值的差值,并计算所有差值的均值与方差平方和的开方结果;

②以式(6)为基础,计算方程右边同方程左边所有外测弹道加速度数值的差值,并计算所有差值的均值与方差平方和的开方结果;

③综合步骤①、步骤②中的开方结果得到所有弹道的综合误差结果,取误差最小弹道为最优弹道。

令(),(),…,()和(),(),…,()分别为参与择优的所有弹道的外测速度函数和外测加速度函数,其中,为弹道数量。(,,,,)和(,)分别为遥测角度函数和遥测视加速度函数。

首先计算所有外测弹道速度方向余弦与遥测角度测量函数差值,令起始位置=0,则这些弹道与遥测角度函数的差值可表示为

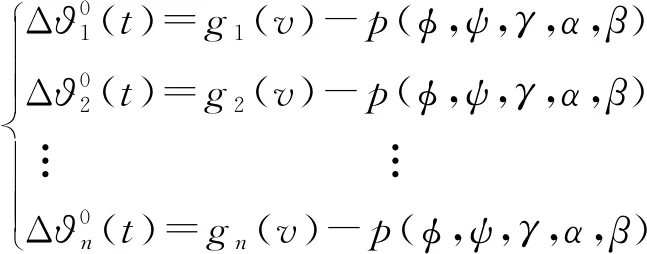
(11)

式中:∈[0,Δ],Δ为采样间隔,为加权点数。则任意弹道对应的差为

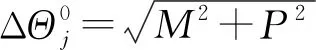
(12)

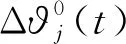
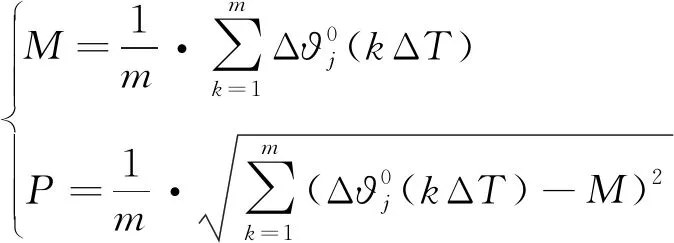
(13)

同理,进行遥测视加速度函数与外测加速度差值计算,令起始位置=0,则差值可表示为

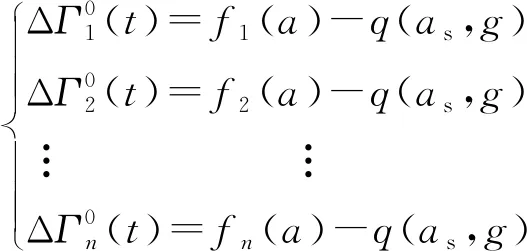
(14)

则弹道的差值可表示为

(15)

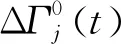
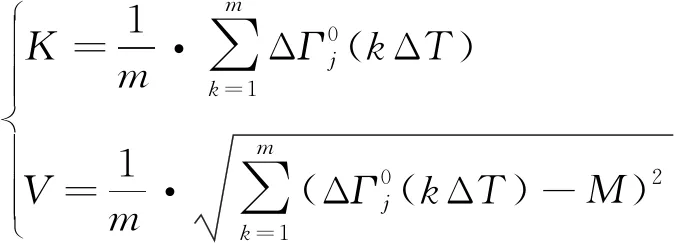
(16)

联合式(12)和式(15),得出各外测弹道的综合误差为

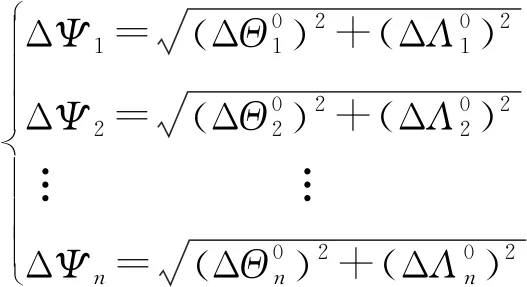
(17)

计算最小综合误差弹道:

=min(Δ,Δ,…,Δ)

(18)

则最小综合误差对应的外测弹道即为弹道择优结果。

4 仿真和实验验证

4.1 遥测角度同外测速度关联模型仿真验证

以某理论弹道数据、理论遥测参数为输入,仿真验证关联模型的正确性。图2为遥测角度同外测速度关联模型在各方向的误差,纵坐标(无量纲)为关联模型误差,具体误差数值见表1。表中综合误差为误差值与误差方差平方和开根号。由表1可知,在发射坐标系方向、方向和方向的关联模型综合误差分别为0.000 76,0.000 64和0.000 32,误差很小,从而验证了关联模型的正确性。

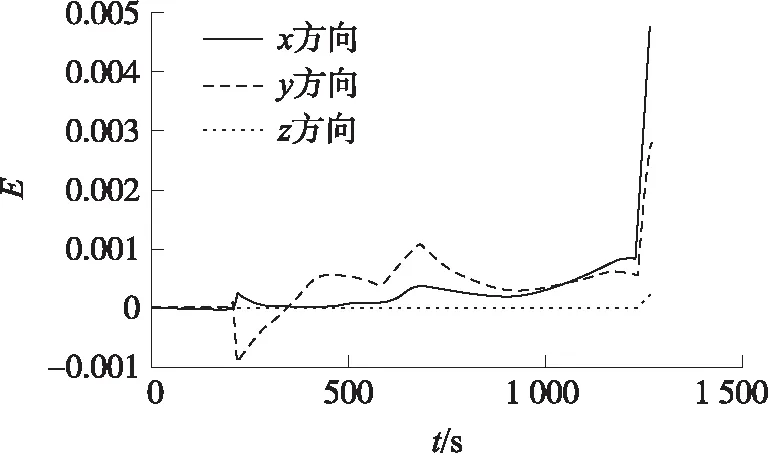
图2 遥测角度同外测速度关联模型误差

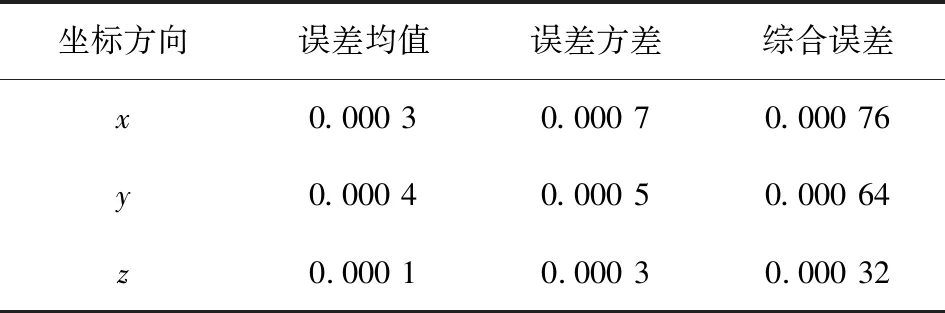
表1 遥测角度同外测速度误差统计结果

4.2 遥测视加速度同外测加速度关联模型仿真验证

以某火箭理论弹道数据、理论遥测参数为输入,仿真验证关联模型的正确性。图3为外测加速度计算值(通过式(6)右边遥测量计算)与实际值之间的误差,图中,为加速度误差。具体误差数值见表2。由表2可知,关联模型综合误差在方向、方向和方向分别为0.071 3 m/s,0.100 2 m/s,0.017 0 m/s,误差很小,从而验证了模型的正确性。

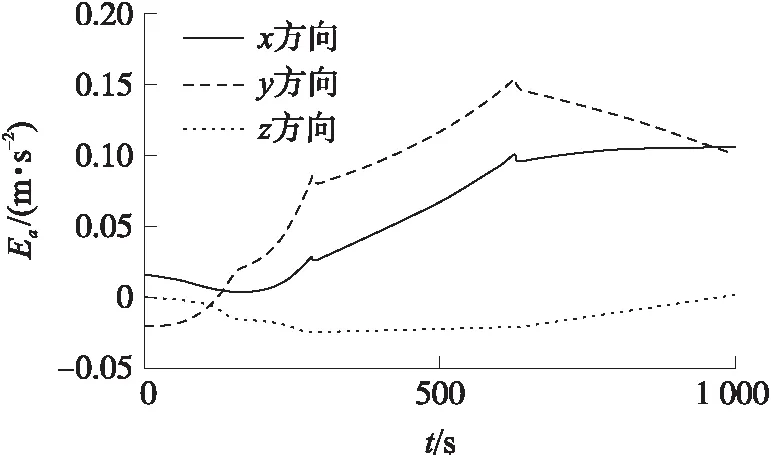
图3 外测加速度计算值与实际值之间的误差

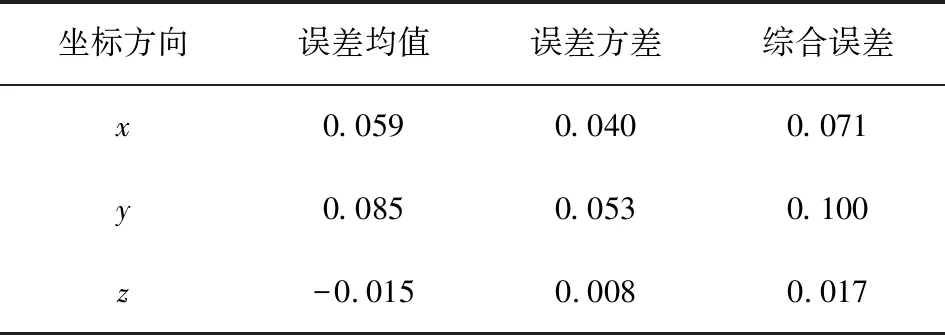
表2 外测加速度计算值与实际值误差统计结果

4.3 外弹道择优方法验证

以某火箭实时测量弹道数据为输入,将弹道分成5类,即摄影经纬仪弹道、光学经纬仪弹道、脉冲雷达弹道、连续波雷达弹道及GNSS差分弹道(分别对应弹道1～弹道5),每类弹道又由很多条设备弹道组成。首先在每类弹道中应用择优方法进行弹道择优,得到5条局部择优弹道。而后在5条局部最优弹道中进行选优,得到全局择优弹道。

为了评估各择优弹道(5条局部择优弹道和全局择优弹道)的精度,分别将它们同事后高精度弹道作差,得到不同的弹道误差,最后将全局择优弹道的误差同5条局部择优弹道的误差进行比较。如图4所示为误差比较图,图中,为弹道误差。图4(a)～图4(e)分别对应连续波雷达局部择优弹道、GNSS差分择优弹道、摄影经纬仪局部择优弹道、光学经纬仪局部择优弹道、脉冲雷达局部择优弹道同全局择优弹道的误差比较。由图4可知全局择优弹道的综合误差最小,从而验证了弹道择优方法的正确性。

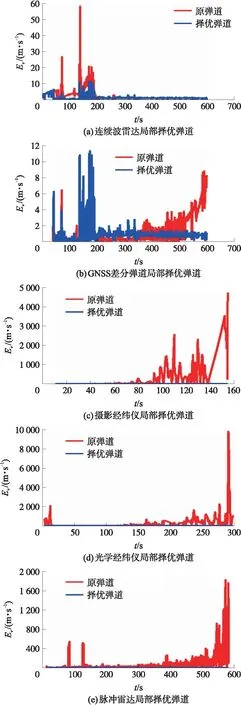
图4 各局部择优弹道误差同全局择优弹道误差比较

5 结束语

本文构建了遥测角度同外测速度、遥测视加速度同外测加速度的关联模型,通过仿真验证了关联模型的正确性。提出了一种基于遥测信息的外弹道择优方法,并通过实际测量数据验证了方法的正确性和有效性。由全局择优弹道、其他择优弹道同事后高精度弹道比对误差可知,全局择优弹道的综合误差最小,从而证明了择优方法的正确性。基于遥测信息的外弹道择优方法正确建立了某些关键遥测信息同外测弹道信息的关联模型,能够选择出精度较高的外测弹道,从而能够为指控中心提供更多的弹道择优辅助决策手段,具有较强的理论应用价值。