形面精度可调节的单层索网空间抛物面天线

李昊，邓泽华，李奇

上海卫星工程研究所，上海 201109

1 引言

超大口径高形面精度空间可展开天线反射面是提升空间天线电性能的关键。天线基本理论表明，通过提升空间天线反射面的口径，能够显著提升天线的增益、带宽及通信容量[1]。空间可展开天线目前可分为三大类，即固面反射面天线、金属网反射面天线及充气反射面天线。固面反射面天线的优点是形面精度高，但随着天线口径的增加，固面反射面的质量及收拢后的体积难以满足运载要求[2]。与固面反射面天线相比，充气式空间可展开天线具有极小的质量及收拢尺寸[3-5]。然而，充气式天线反射面存在热变形较大及气体泄漏的问题，导致其展开后的形面精度较低[6]。同时，充气式反射面需要额外的气瓶及压缩机，对于超大口径空间天线，这些设备将导致明显的额外质量。相比之下，网面天线具有相对均衡的特性。网面天线根据其支撑结构，可分为折叠肋式、辐射肋式及周边桁架式。其中，近二十年来受到国内外学者对周边桁架式空间可展开网面天线(也称为AstroMesh天线)进行了大量的研究[7,8]，包括高精度网面设计方法[9]、天线形面调整方法[10]以及天线展开动力学[11,12]等。目前，周边桁架式空间可展开网面天线已经实现了在轨应用。超大口径的周边桁架式天线，其缺点是天线反射面的焦距通常将达到几十甚至上百米。对于一个50 m口径的周边桁架式天线，当天线的高度为5 m时，其反射面抛物面的弦高则小于5 m，天线的焦距将大于62 m。超大的天线焦距，将需要一个额外的展开机构或机械手来保证天线反射面和天线馈源之间的距离，或者通过复杂的二次、三次反射设计方案才能完成，这将给航天器的总体设计带来困难。

周边桁架式天线，其索网系统中通常包括前网、后网及竖向拉索。周边桁架式天线，其索网的最终形状取决于索网的拓扑构型及索网的内部张力。目前，周边桁架式天线在设计过程中，通常采用力密度法[13,14]及动力松弛法[15]进行索网找形。由于天线索网的形状与索网内部张力相互耦合，因此通常难以直接计算出形成抛物面反射面所对应的绳索张力。在周边桁架天线的找形研究中，需先给定一个初始绳索张力，并通过多次迭代修改绳索的张力，直至天线反射面的形状达到设计要求[16]。即使找形设计精确计算出了每根绳索的张力，但在实际制造过程中，对于超大型的索网结构，在制造误差、安装误差、重力、弹性变形等因素的影响下，通常难以根据设计结果精确地调整每根绳索的张力。截至目前，国内外尚没有发展出一个通用性的理论来提升超大口径索网天线的制造形面精度，天线形面精度的提升主要依靠生产制造方的经验。

当天线发射入轨之后，在空间环境下天线将产生热变形，进而影响天线的在轨形面精度。为实现高形面精度的空间可展开天线，需根据天线的在轨变形，对天线反射面进行在轨调整[17-18]。对于超大口径的空间可展开网状天线，由于天线中具有数量巨大的绳索，已有的调整方案通常需要大量的作动器来实现天线形面调节。大量的作动器将降低天线整体的可靠性，增加天线的质量及能耗，工程实现性较差。目前，国内外尚未见天线形面调节系统的在轨应用报道。

综上，周边桁架式天线是实现超大口径空间可展开天线的可行方案，但周边桁架式天线存在着焦距大、内部张力复杂、精确制备困难及在轨调节难度大等难以解决的问题。为实现超大口径的空间可展开天线，提出了一种新型可在轨调整的单层索网天线。首先基于能量法，建立了新型单层索网空间可展开天线的找形理论，预测了天线索网中绳索的设计张力，并说明了天线在轨形面调整的原理。基于理论分析结果，建立了天线的有限元模型，通过数值仿真对理论分析结果进行验证。

2 形面可在轨调节大口径空间可展开天线基本原理

2.1 天线设计及找形

新型形面可在轨调节大口径空间可展开天线的结构形式及平面拓扑如图1所示。文中的新型天线只包含一层索网，下文称之为单层索网天线。单层索网天线的反射面由多个环向可折叠杆及径向拉索组成，环向可折叠杆能够实现环向折叠收拢，展开后起环向支撑作用。单层索网天线的中心轴处为可折叠的中心支撑柱，中心支撑柱与天线反射面之间采用多根径向绳索连接，中心支撑柱展开后对天线索网反射面施加竖向张紧力。图1中的单层索网天线，其反射面口径为50 m，焦距f=10 m，反射面方程为z=0.025(x2+y2)。反射面中包括24根环向支撑肋、60根径向均匀分布的绳索。24根环向支撑肋的直径以2 m的间隔逐渐从4 m增加到50 m，各个环向支撑肋之间通过径向绳索连接。

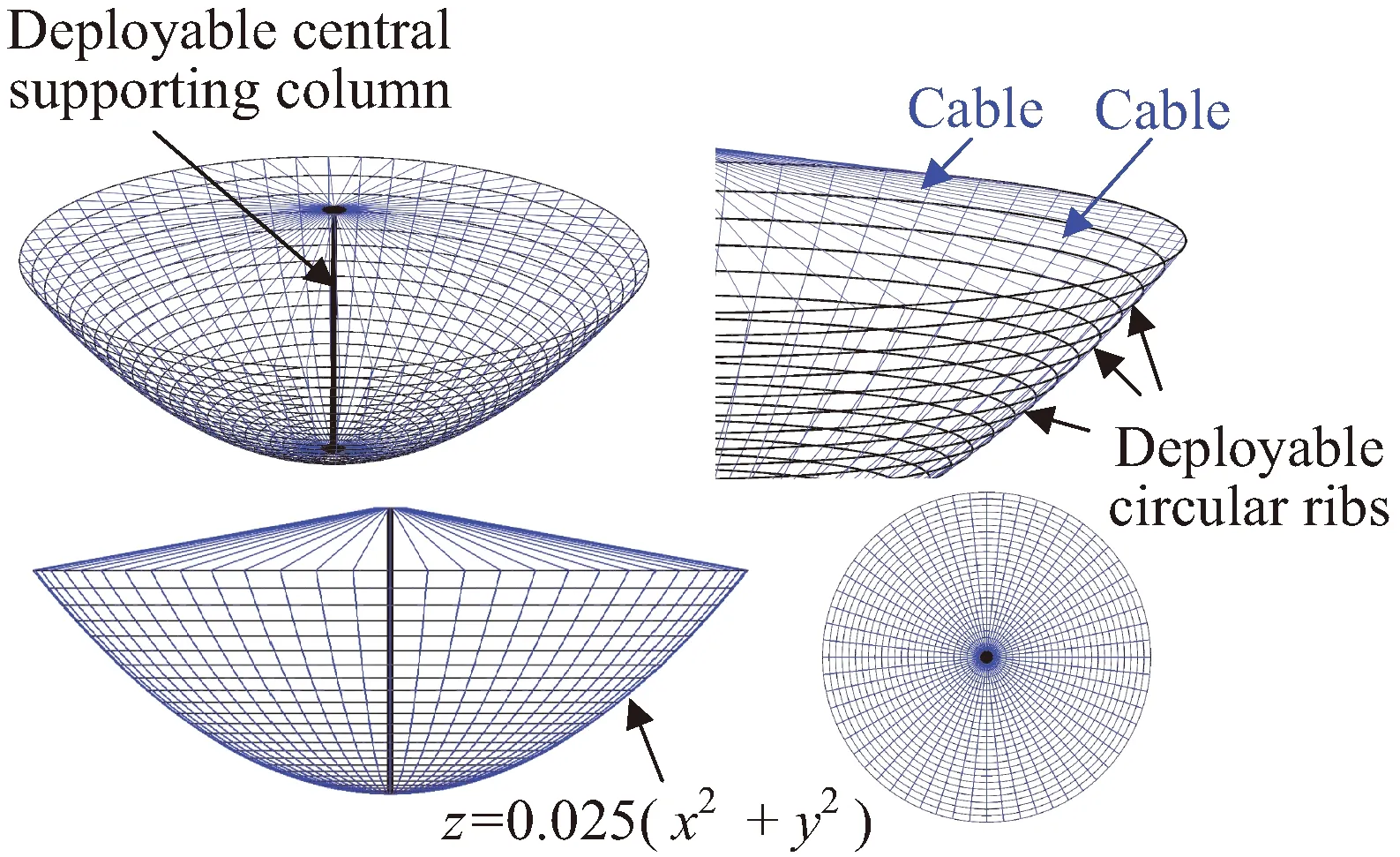
图1 50 m口径单层索网空间可展开天线示意Fig.1 Sketch map of proposed 50 m-diameter one-layer cable-net antenna

单层索网天线为轴对称结构，因此可将其进行简化以进行静力平衡分析，如图2所示，其中每个节点表示环向支撑肋。单层索网静止状态下，由于没有外力作用，每一根环向支撑肋在竖直方向上的合力为0。

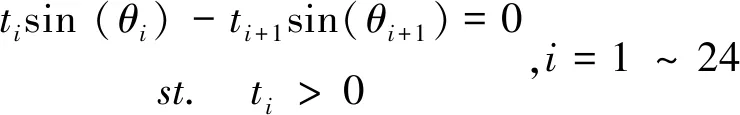
(1)

式中：θi为每根绳索与水平方向之间的夹角；ti表示绳索拉力。理想情况下，单层索网在平衡位置处，每个环向支撑肋的位置应与目标旋转抛物面相重合。反映到图2中，即每个节点应处于抛物线z=0.025x2上。因此，当绳索张紧之后，绳索与水平面的夹角θi可通过环向支撑的理想坐标计算得到，并且θi<θi+1,i=1～23。通过式(1)可知，绳索拉力满足关系ti>ti+1,i=1～23。因此，可推导图2中每个节点在水平方向的静力平衡方程：

ticosθi-ti+1cosθi+1=Fi,i=1～23

t24cosθ24+t25cosθ25=F24

(2)

式中：Fi表示环向支撑肋施加在绳索上的力。水平向的静力平衡方程表明，环向支撑肋在天线张紧状态下受压。方程(1)及方程(2)中，共有48个平衡方程，而具有49个未知力Fi和ti。因此，方程(1)及方程(2)不可解。为求得单层索网中的内部绳索张紧力ti和环向支撑肋的径向支撑力Fi，可以先给定一个绳索力ti或径向支撑力Fi，将方程(1)及方程(2)中的未知参数减少至48个，则可求解得到另外48个未知力。本文中，假设绳索张力t1已知。

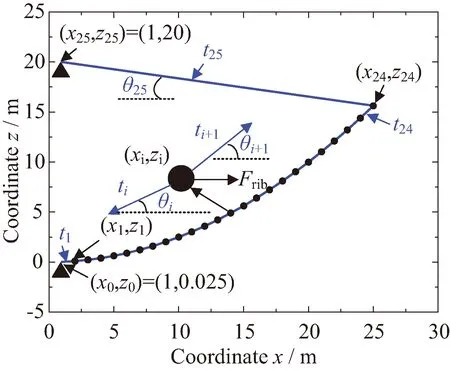
图2 单层索网静力平衡分析Fig.2 Force equilibrium analysis of cable-net

单层索网张紧后，环向支撑肋受压，绳索受拉，环向支撑肋及绳索都将产生弹性变形。为了保证单层索网发生弹性变形后与目标旋转抛物面重合，需根据所计算的绳索张力ti及环向支撑肋径向支撑力Fi来计算每段绳索的初始长度及每个环向支撑肋的初始半径。由于环向支撑肋承受均匀的压力，忽略环向支撑肋局部弯曲变形，在60根径向绳索的压力下，环向支撑肋任一截面所受的压力为：

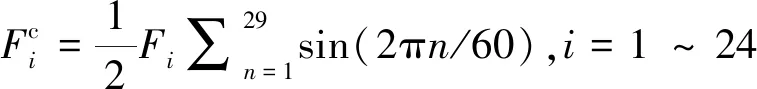
(3)

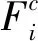
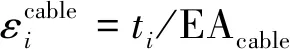
(4)

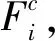
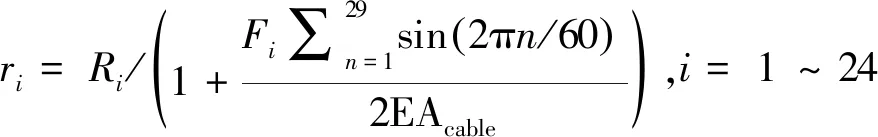
(5)

式中：li为绳索的初始制造长度；ri为环向支撑肋的初始制造半径；Li和Ri分别表示每段绳索及每个环向支撑肋的设计长度及设计半径。Li和Ri为已知量，可以通过图2中的节点坐标计算得到。通过式(5)计算得到li和ri后，下一步需计算单层索网张紧后的实际平衡位置。本文以图2中各个节点的坐标xi和zi为未知量，计算绳索的整体弹性应变能：

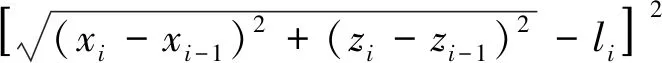
(6)

为了推导环向支撑肋的弹性应变能，将环向支撑肋等效成径向压缩弹簧。等效压缩弹簧自由状态下的初始长度为ri，承受压力Fi后，等效压缩弹簧的变形量为：

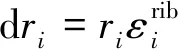
(7)

将式(3)，式(4)代入式(7)后，得到环向支撑肋的径向等效压缩刚度：

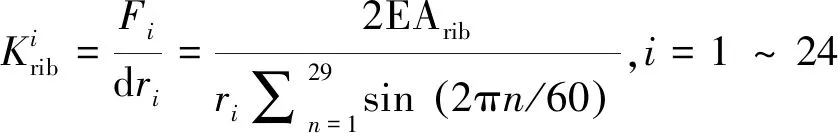
(8)

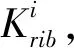
(ri-xi+1)2

(9)

在式(6)及式(9)中，参数60表示在天线环向共有60组拉索。单层索网的整体应变能为：

∏antenna=∏cable+∏rib

(10)

由图2可知，在对称截面上，第1根绳索及第25根绳索一端分别与中心支撑轴相连，则第1个节点及第26个节点的坐标已知，分别为x0=1,z0=0.025和x25=1，z25=20。基于能量法，将天线总体应变能对未知节点坐标xi和zi微分，可得到一组非线性方程组：

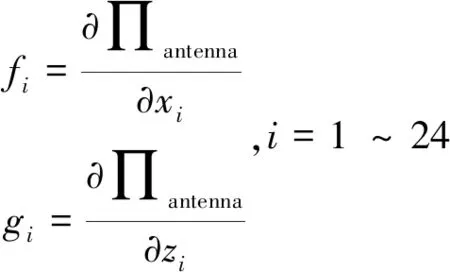
(11)

通过求解式(11)，将得到图2中每个节点的坐标，即单层索网中环向支撑肋的平衡位置。本文采用了Mathematica软件对式(11)进行求解，求解采用函数为“FindRoot”。

以上为单层索网天线的找形过程。第一步，通过给定一个绳索初始力t1，并通过式(1)～式(3)求得单层索网天线内部绳索的张力及环向支撑肋的压力；第二步，通过式(5)计算天线绳索及环向支撑肋的初始制造长度和初始制造半径；第三步，通过式(10)计算天线的整体应变能，并通过式(11)计算天线环向支撑肋的平衡位置。

2.2 天线形面精度调整

假设t1=50 N，通过式(1)～式(3)求得的绳索张力ti及环向支撑肋截面压力Fci见图3所示。随着绳索和环向支撑肋离天线中心轴的距离逐渐增加后，对应的ti和Fci逐渐降低。由于第25根绳索一端与天线中心轴连接，其切向角度θ25发生突变，因此第25根绳索及第24根环向支撑肋的内力相对较大。图3显示，当t1=50 N时，天线绳索的最大拉力不超过50 N，环向支撑肋的最大截面压力为449.7 N。假设EAcable=103N，EArib=2.5×106N，计算得到的绳索初始制备长度及环向支撑肋初始制备半径见表1。计算结果显示，由于环向支撑肋的内部压力较小，环向支撑肋的初始制备半径与设计半径之间的差异非常小，说明在天线设计过程中，环向支撑肋的弹性变形可忽略不计。

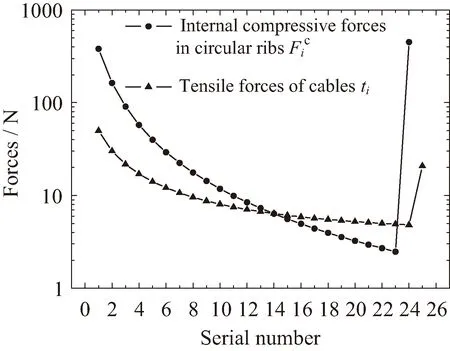
图3 环向支撑肋截面压力及绳索拉力计算结果，(t1=50 N)Fig.3 Compressive forces of circular ribs and tensile forces of cables,(t1=50 N)

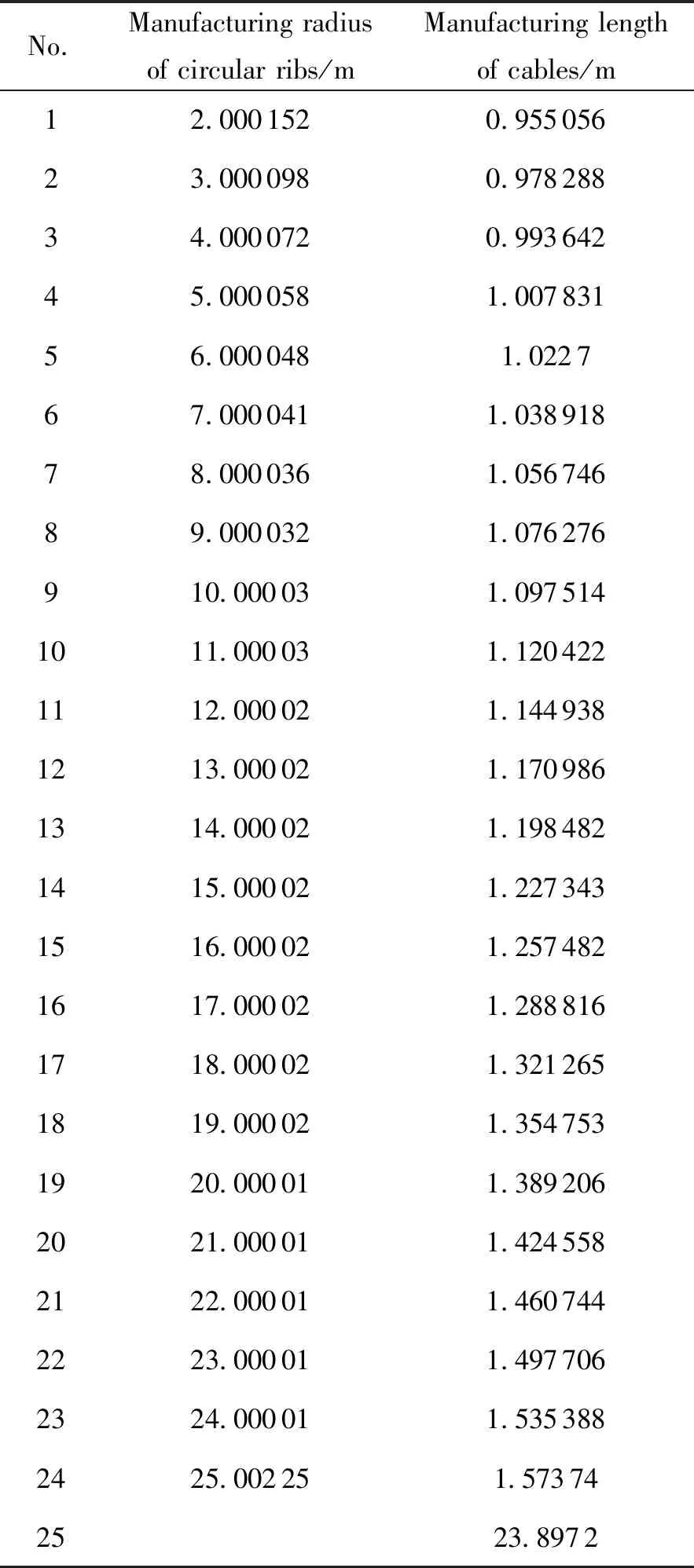
表1 绳索初始制造长度及环向支撑肋初始制造半径,(t1=50 N)

基于表1中的初始长度，通过公式(11)将计算得到单层索网天线的稳定构型，其稳定构型的对称截面如图4所示。在计算过程中，通过调整坐标z25可改变天线的中心轴高度。预测结果显示，当z25=20 m时，天线张紧后的平衡位置与设计抛物面z=0.025(x2+y2)完全吻合。当调整天线的中心轴高度z25后，天线张紧后的反射面形状随之发生变化。因此，图4说明，单层索网天线结构，可通过调整中心轴的高度，实现天线反射面形状的调整。在实际工程设计中，可通过在天线中心轴上安装调整机构，通过调整天线中心轴的长度，实现天线形面的在轨调整。

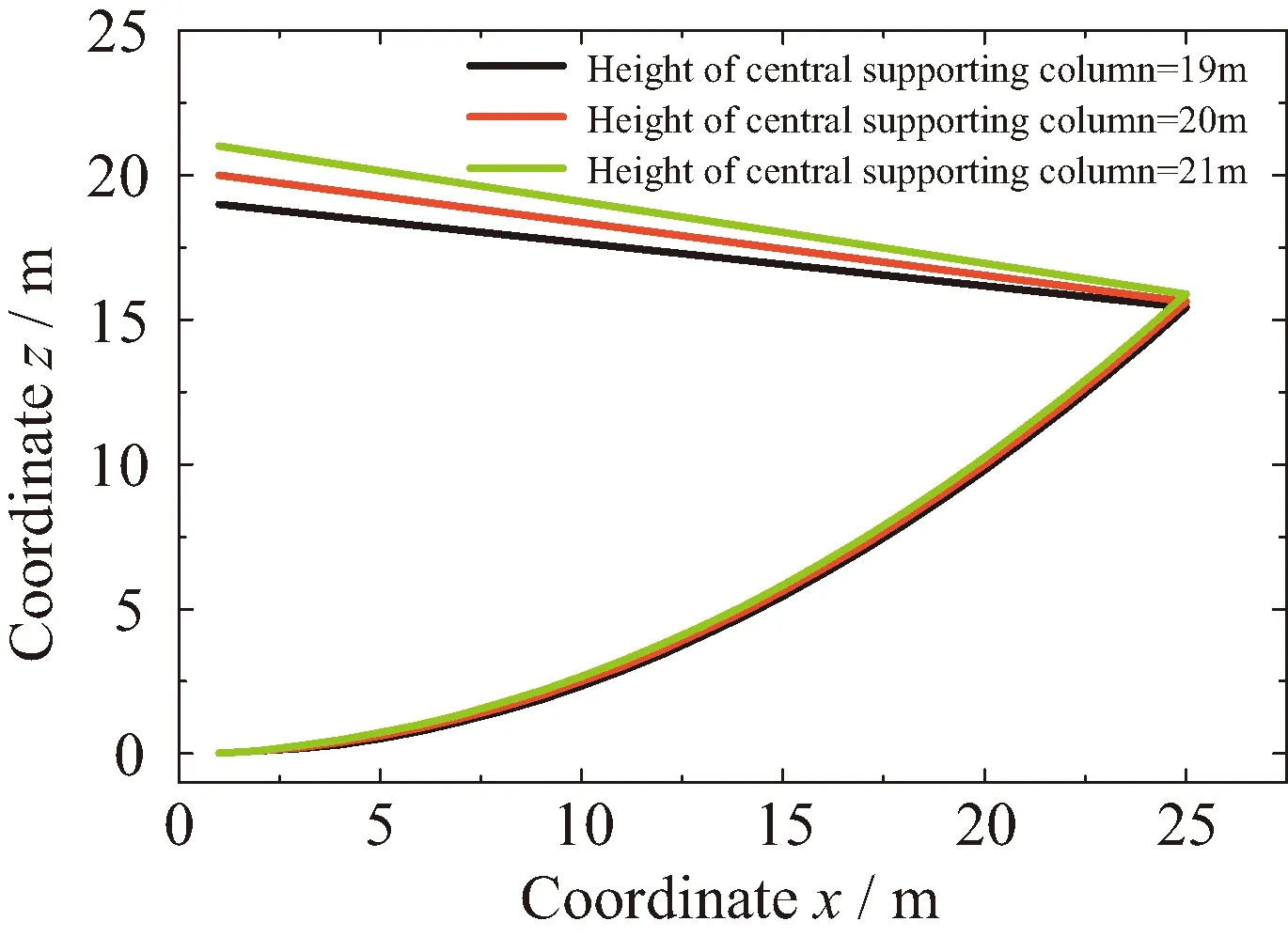
图4 不同中心轴高度下单层索网天线反射面对称截面的稳定构型预测结果，(t1=50 N)Fig.4 Predicted static shapes of the cable-net with different central column height,(t1=50 N)

在轨状态下，由于天线索网将不可避免地产生热变形，进而降低天线的在轨形面精度。为了验证单层索网天线能够实现在轨形面调整，以抵消索网热变形的影响，本文假设天线的绳索在轨产生±1%的热应变，并预测天线产生热应变后的形状。为了在天线模型中考虑热应变，在表1中的绳索制备长度上施加±1%的长度误差，代入理论模型中计算天线的稳定构型，计算结果如图5所示。理论预测结果显示，考虑绳索热变形后，天线反射面的形状将产生明显变化，天线的形面精度将明显降低。

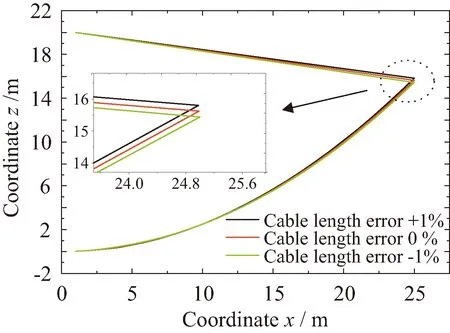
图5 天线绳索产生±1%热变形后的天线形状预测结果，(t1=50 N)Fig.5 Predicted cable-net shape with ±1% error of cable length,(t1=50 N)

为了计算天线的形面精度，通过式(11)的预测结果，可推导得到天线反射面所有绳索与环向支撑肋交点的空间坐标。基于所有节点的空间坐标，可通过最小二乘法拟合得到一个新的旋转抛物面。相对于新拟合的旋转抛物面，可计算得到天线反射面的形面均方根误差RMS[Δi]。通过改变天线中心轴的长度，在考虑0.1%和-0.1%的绳索热变形后，天线反射面的形面误差预测结果如图6所示。图6(a)显示，当天线中心轴的长度保持20 m不变时，天线绳索产生0.1%和-0.1%的热变形后，天线的形面误差分别为15.8 mm和15.68 mm。当调整天线的中心轴长度后，天线反射面的形面精度能够分别降低至4.89 mm和4.7 mm。因此，通过调整天线中心轴的长度，可有效降低天线热变形对形面精度的不利影响。图6(b)显示，天线的形面误差随着绳索热变形线性增加。在不同水平的热变形情况下，通过调整天线的中心轴长度，都能够有效降低热变形导致的形面误差。

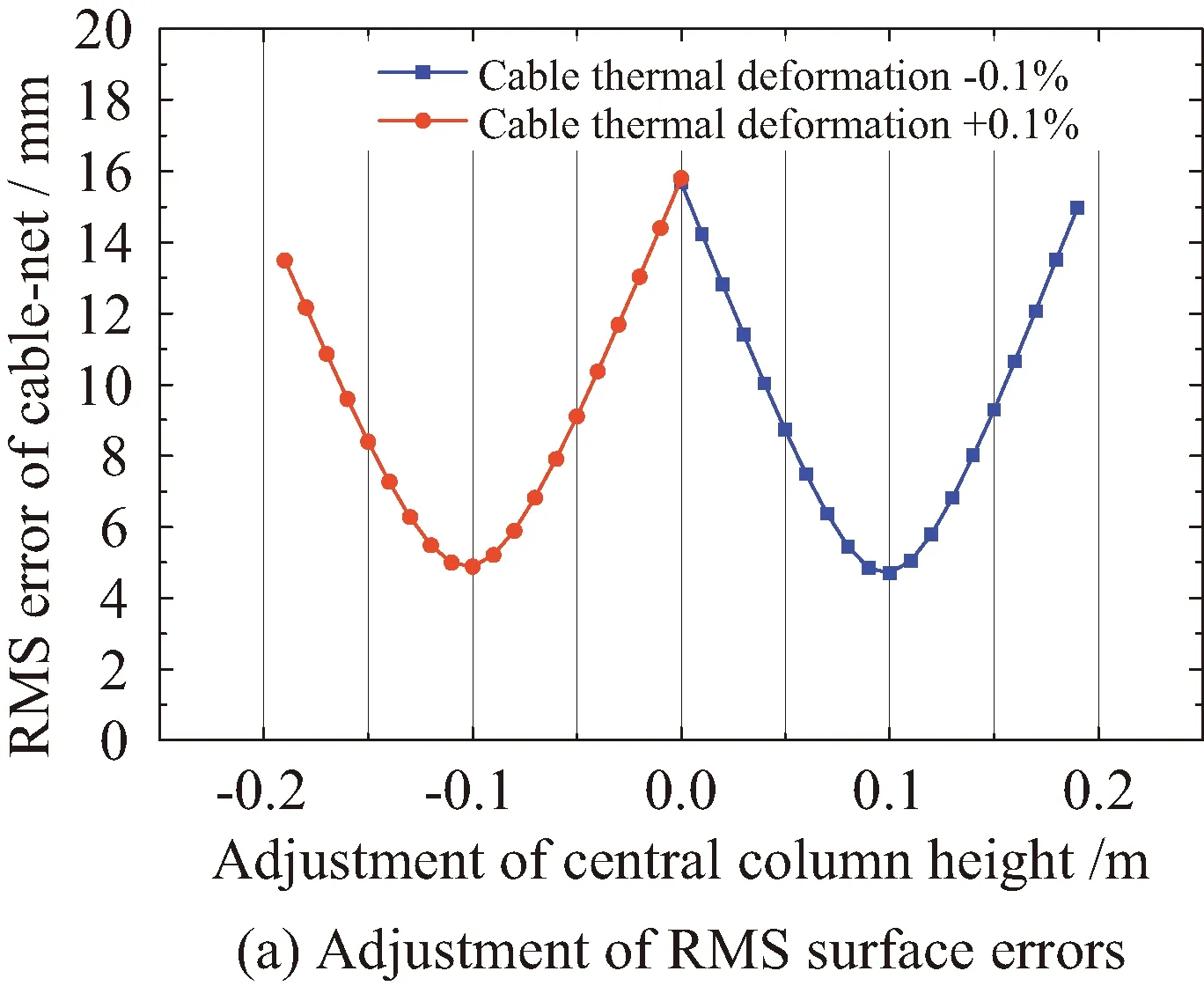
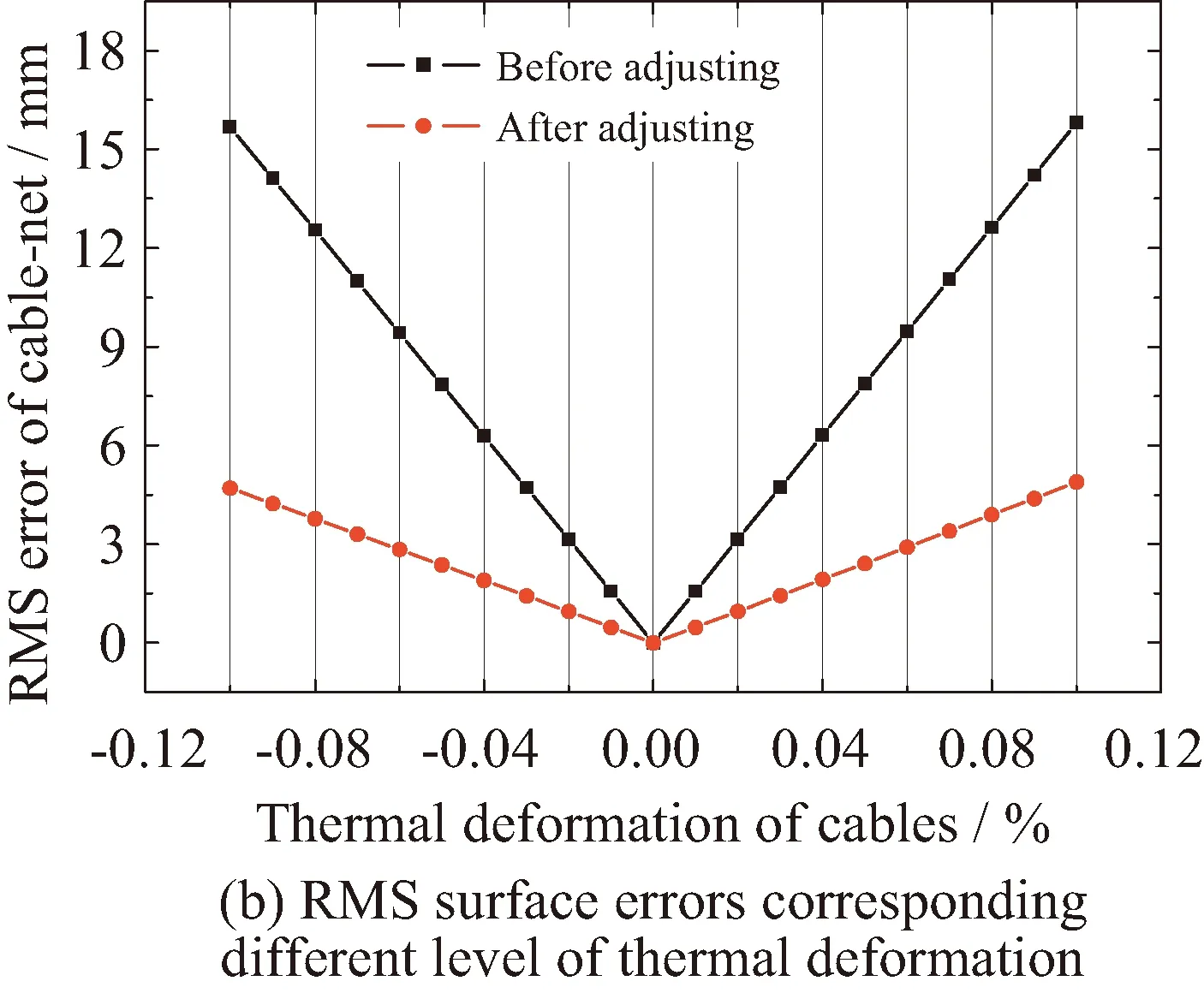
图6 天线反射面形面误差预测结果(t1=50 N)Fig.6 The RMS error of cable-net nodes with respect to the new fitted parabola curve(t1=50 N)

3 数值仿真验证

为了采用数值仿真方法验证单层索网天线，本文对图1中50 m口径单层索网的结构进行了初步设计，并基于结构设计建立了天线的有限元模型。

3.1 结构设计

50 m口径单层索网天线的收拢状态及展开状态如图7及图8所示。环向支撑肋由碳纤维复合材管制成。为实现轻量化、可折叠及高可靠的折叠结构，采用复合材料卷尺弹簧铰链代替常规的金属铰链结构，驱动环向可折叠杆及天线中心可折叠轴实现收拢展开。通过在复合材料管件上设置贯穿的孔洞，可实现复合材料卷尺弹簧铰链(tape-spring hinge)的功能[19-20]。复合材料卷尺弹簧铰链，具有结构简单，恒扭矩及自锁定的特性[21]。收拢状态下，天线环向支撑肋在复合材料卷尺弹簧铰链处折叠，并可实现层层叠加收拢。天线整体收拢后的尺寸为Φ3 000 mm×3 150 mm。天线在轨释放后，环向支撑肋在复合材料卷尺弹簧铰链的驱动下展开。

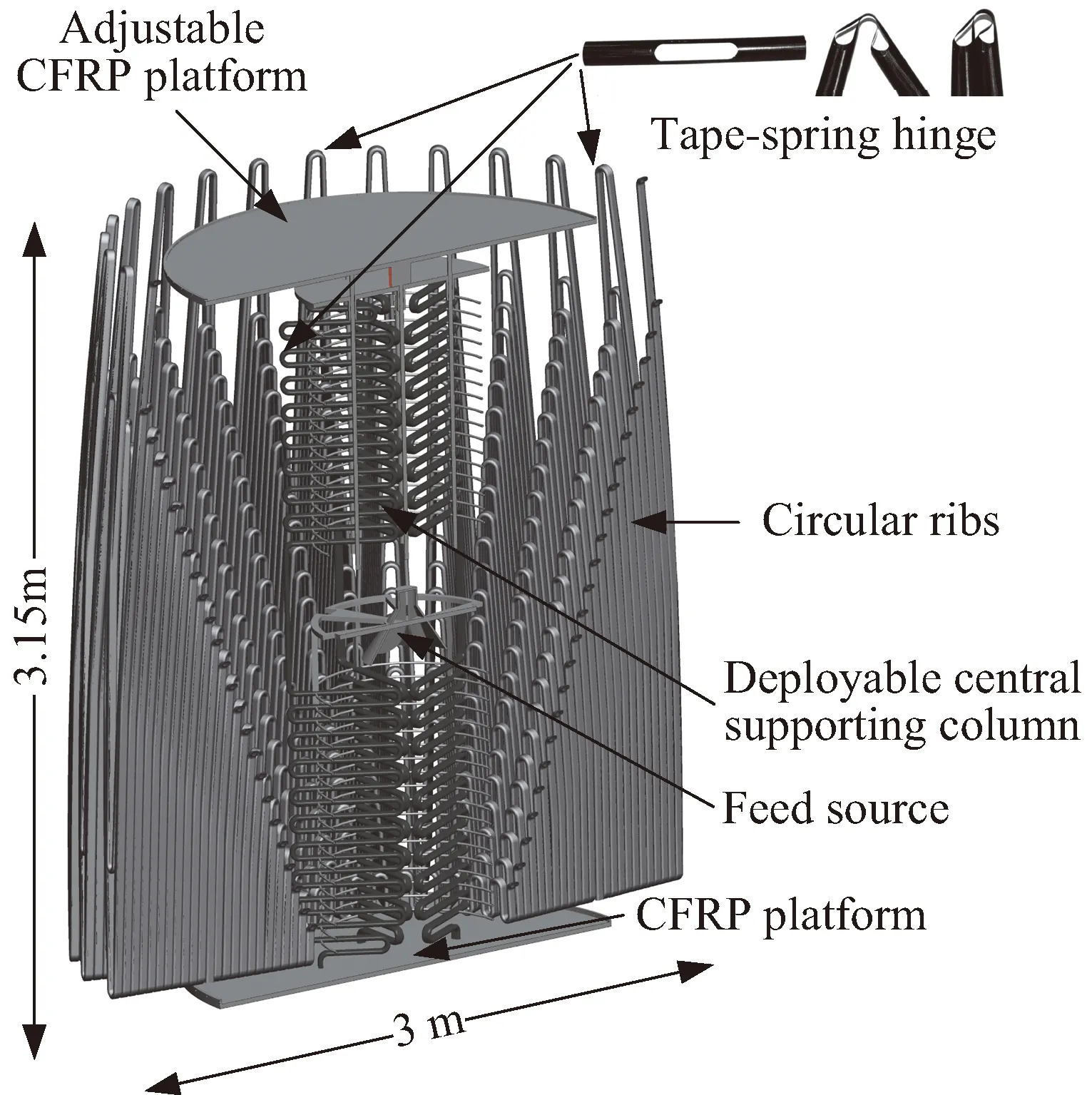
图7 50 m口径单层索网天线收拢状态Fig.7 Stowed state of the one-layer cable-net antenna with the aperture of 50 m (The photo of tape-spring hinge is quoted from [21])

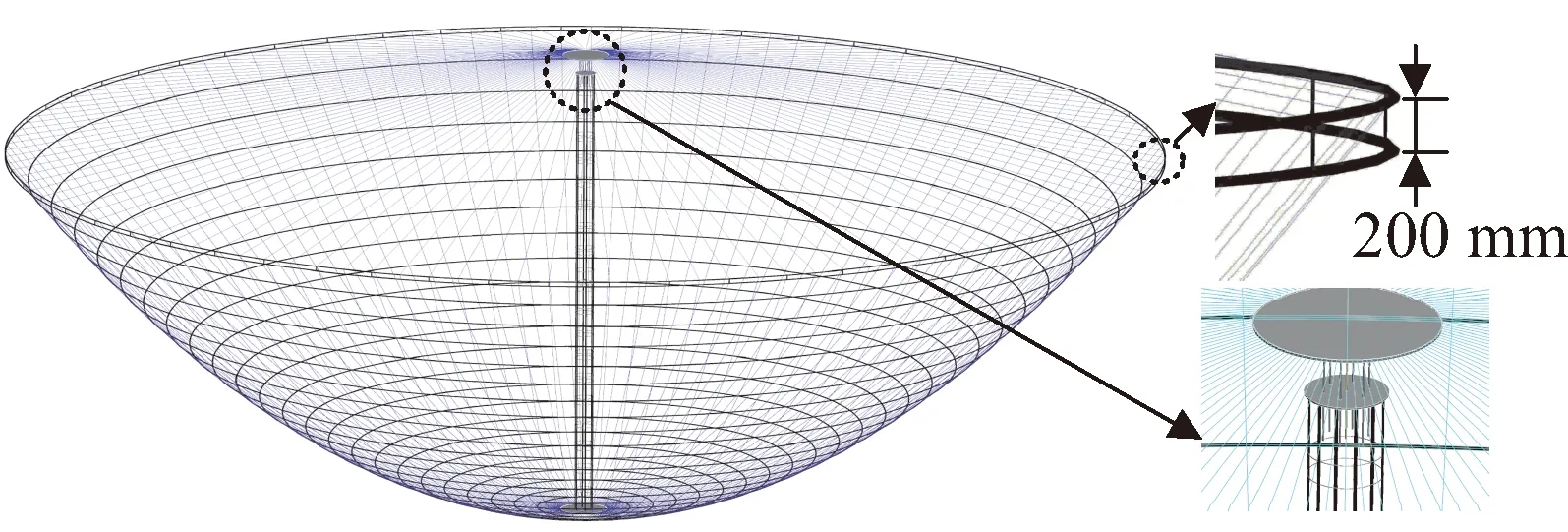
图8 50 m口径单层索网天线展开状态Fig.8 Deployed state of the one-layer cable-net antenna with the aperture of 50 m

对于50 m直径的环向支撑肋，理论分析显示其内部压力相对较大，为避免50 m直径环向支撑肋在压力作用下发生屈曲，设置2根50 m口径环向支撑复合材料管，以增加其整体面外弯曲刚度。对于其它环向支撑肋，由于其内部压力或直径相对较小，因此仅设置一根复合材料管。

天线的中心轴为复合材料管件组成的桁架结构。通过在复合材料管件上开孔，实现卷尺弹簧铰链，复合材料桁架中心轴能够在其长度方向实现收拢。天线的馈源安装在复合材料桁架结构上，天线馈源与天线底部的距离为10 m。天线中心复合材料桁架展开后的长度为19.2 m。中心复合材料桁架顶部安装一个伸缩平台，伸缩平台能够驱动天线反射面进行在轨形面调整。天线中心轴的长度变化范围为19.2 ～20.8 m。

3.2 单层索网天线有限元模型

本文利用有限元软件ABAQUS建立了单层索网天线的有限元模型。天线中复合材料管件采用梁单元B31建模，绳索采用桁架单元T3D2建模，天线中心轴上的可伸缩平台采用4节点壳单元S4建模。单层索网天线的有限元模型如图9所示。对于天线中的复合材料管件，设置梁单元截面尺寸为20 mm×40 mm，截面壁厚为1 mm。设置复合材料的等效材料特性E=20.83 GPa，μ=0.3，则复合材料梁单元的截面刚度为EA=2.5×106N。

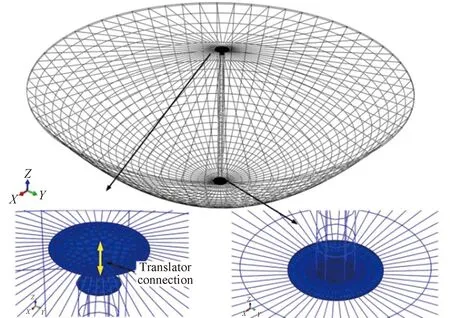
图9 单层索网天线有限元模型Fig.9 Finite element model of the one-layer cable-net antenna

在单层索网天线的设计中，应采用拉伸刚度相对较小的绳索。若采用拉伸刚度较大的绳索，微小的长度误差将会导致绳索内部的张紧力发生较大的变化，进而导致天线内部的绳索张紧力与设计结果之间具有较大误差。因此，本文中采用的绳索拉伸刚度为1 000 N/m。在有限元模型中，绳索桁架单元的直径为1 mm，材料刚度设置为1.27 GPa。

在建模过程中，单层索网中绳索的建模长度及环向支撑肋的建模半径为理想值Li和Ri，而不是制造长度li和ri。为了在模型中建立张紧力，设置绳索材料的热膨胀系数为α=10-5/℃，并在第一个静态分析步中对绳索施加温度变化，通过热变形产生张紧力。无约束状态下，天线绳索发生热变形后的长度与制造长度相等。所施加的温度变化为：

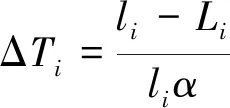
(12)

式中：Li表示绳索在张紧状态下的理想长度，可通过旋转抛物面计算得到；li表示绳索的理想制造长度，通过式(5)计算得到。

为系统分析绳索张力对天线反射面的影响，设置天线绳索张力t1从10 N变化至100 N，并利用有限元模型分别预测了不同绳索张力情况下天线的形面精度及天线的基频t1=10 N和t1=100 N时，天线的弹性变形有限元预测结果如图10所示。有限元分析表明，50 m直径的环向支撑肋在绳索拉力作用下产生了相对明显的局部弯曲变形。在t1=10 N和t1=100 N时，天线反射面最大的局部弹性变形分别为0.402 mm和4.759 mm。

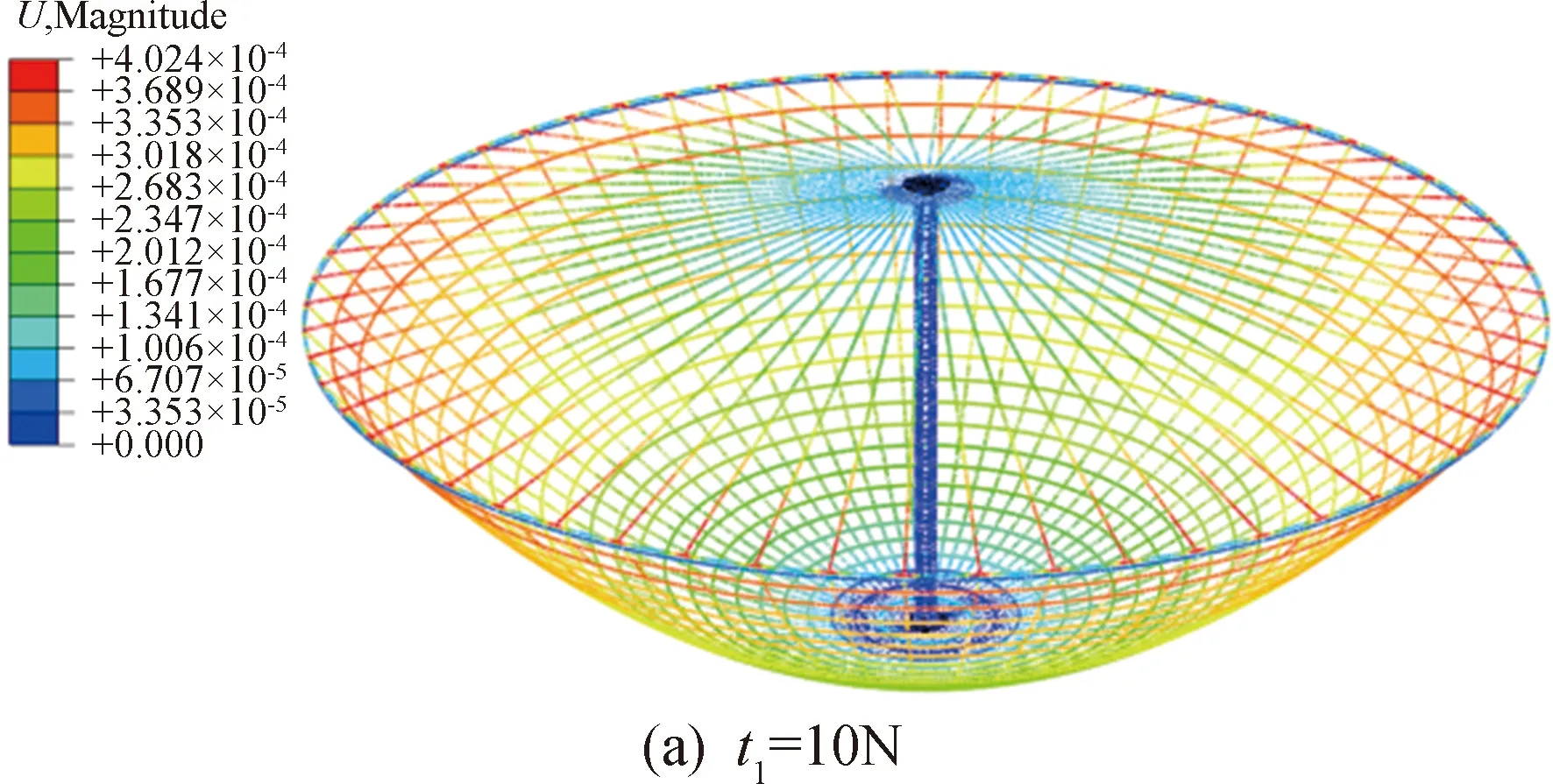
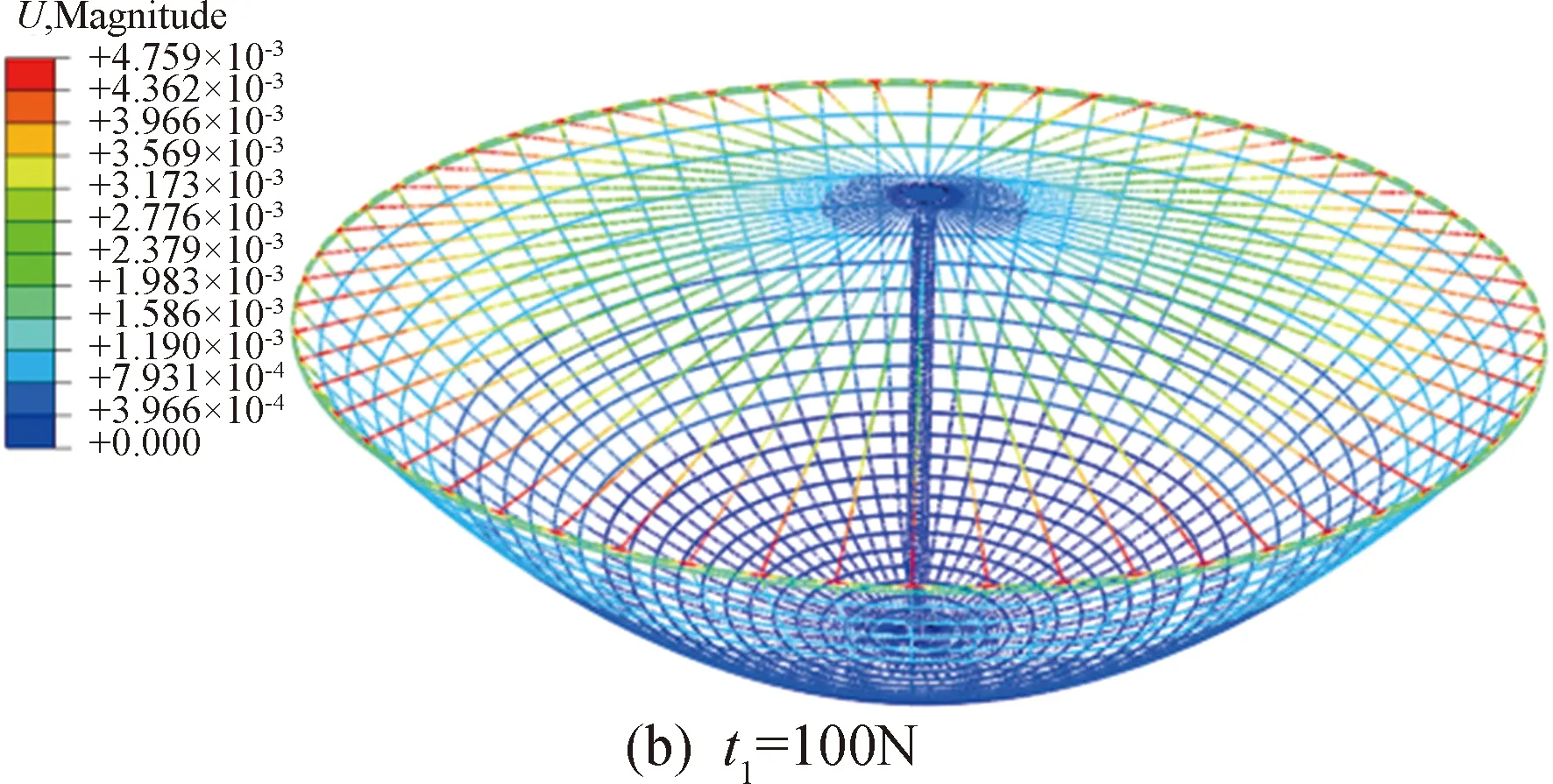
图10 不同张力情况下天线弹性变形有限元分析结果Fig.10 Contour map of node displacement magnitude of cable-net of the antenna, predicted byFEA

为了验证有限元模型中的绳索张力分布与设计状态相同，将不同t1情况下，有限元模型预测的绳索张力与理论计算结果进行对比，对比结果如图11所示。不同张力情况下，有限元模型预测的绳索张力与理论预测结果几乎完全吻合。图11证明采用伸缩热变形能够有效且精确地建立单层索网天线内部张力场。

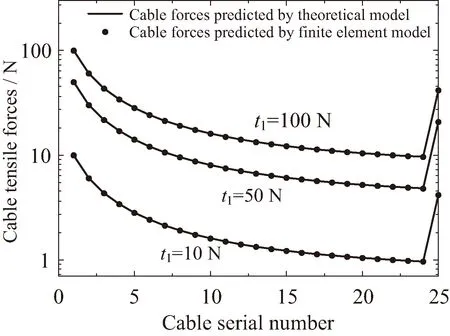
图11 天线张力预测结果对比Fig.11 Comparison of the cable forces predicted by the finite element model against the designed cable forces

理论上，当天线绳索张紧后，天线反射面的各个节点应与设计的旋转抛物面完全吻合。然而，有限元分析显示，天线的环向支撑肋在绳索拉力作用下将产生局部弹性弯曲变形。为评价天线的实际形面精度，本文基于天线变形后的空间坐标预测结果，拟合得到新的抛物面方程，并计算了天线反射面与拟合的新抛物面方程之间的RMS形面误差RMS[Δi]。不同张力情况下的天线形面误差有限元预测结果如图12。有限元分析结果显示，天线的形面误差随着天线张力的增加而线性增加。

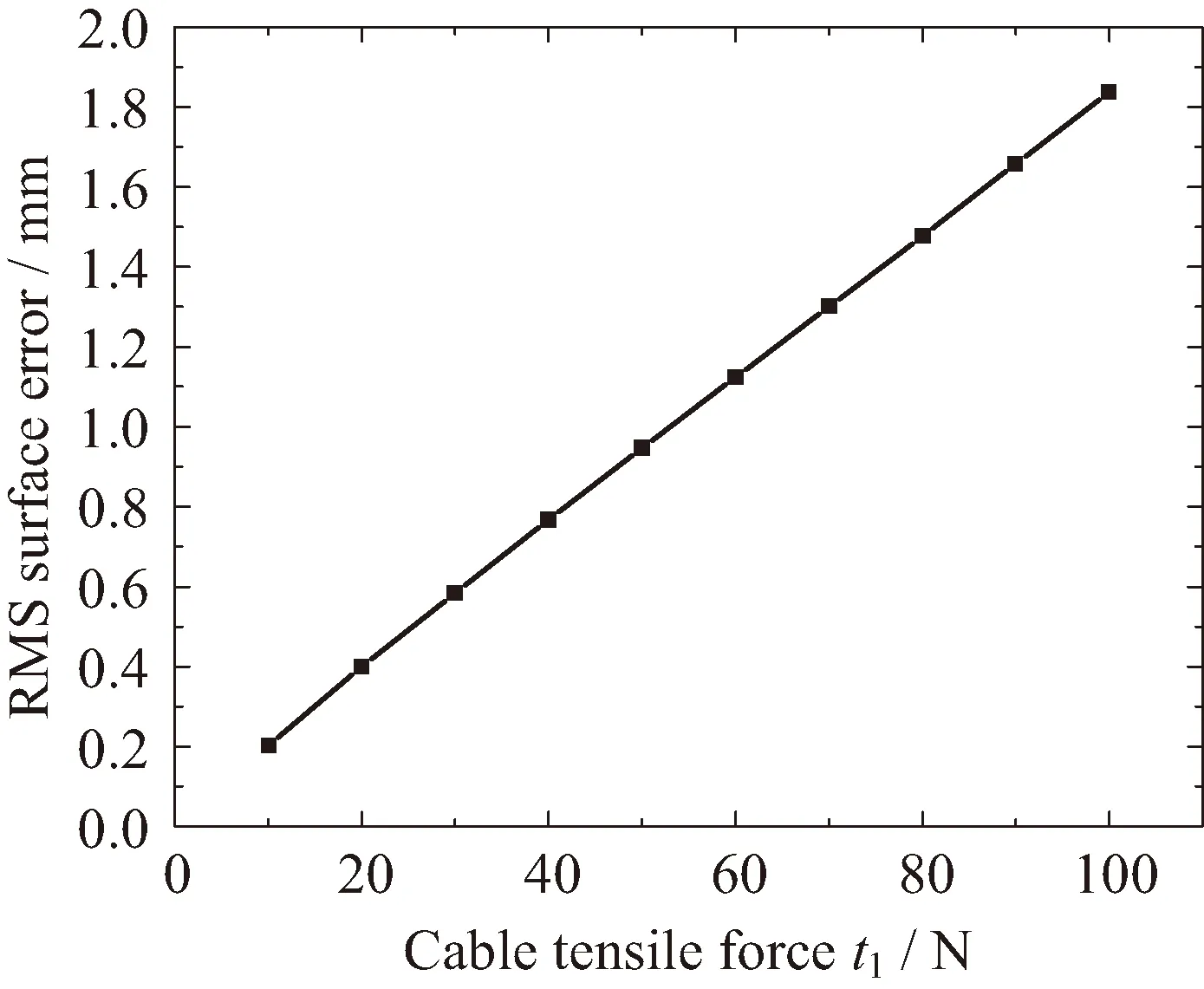
图12 不同绳索张力情况下天线形面误差有限元预测结果Fig.12 RMS surface error of the antenna against the cable tensile force t1

将天线底部固定，天线的模态分析结果如图13所示。天线的一阶模态为旋转模态，天线反射面绕着天线中心轴旋转。不同绳索张力下天线的基频预测结果如图14所示。有限元分析显示，通过增加天线绳索的张力，能够有效提升天线的基频。

图13 单层索网天线第一阶及第二阶模态Fig.13 First two modes of the one-layer cable-net antenna, (t1=100 N)

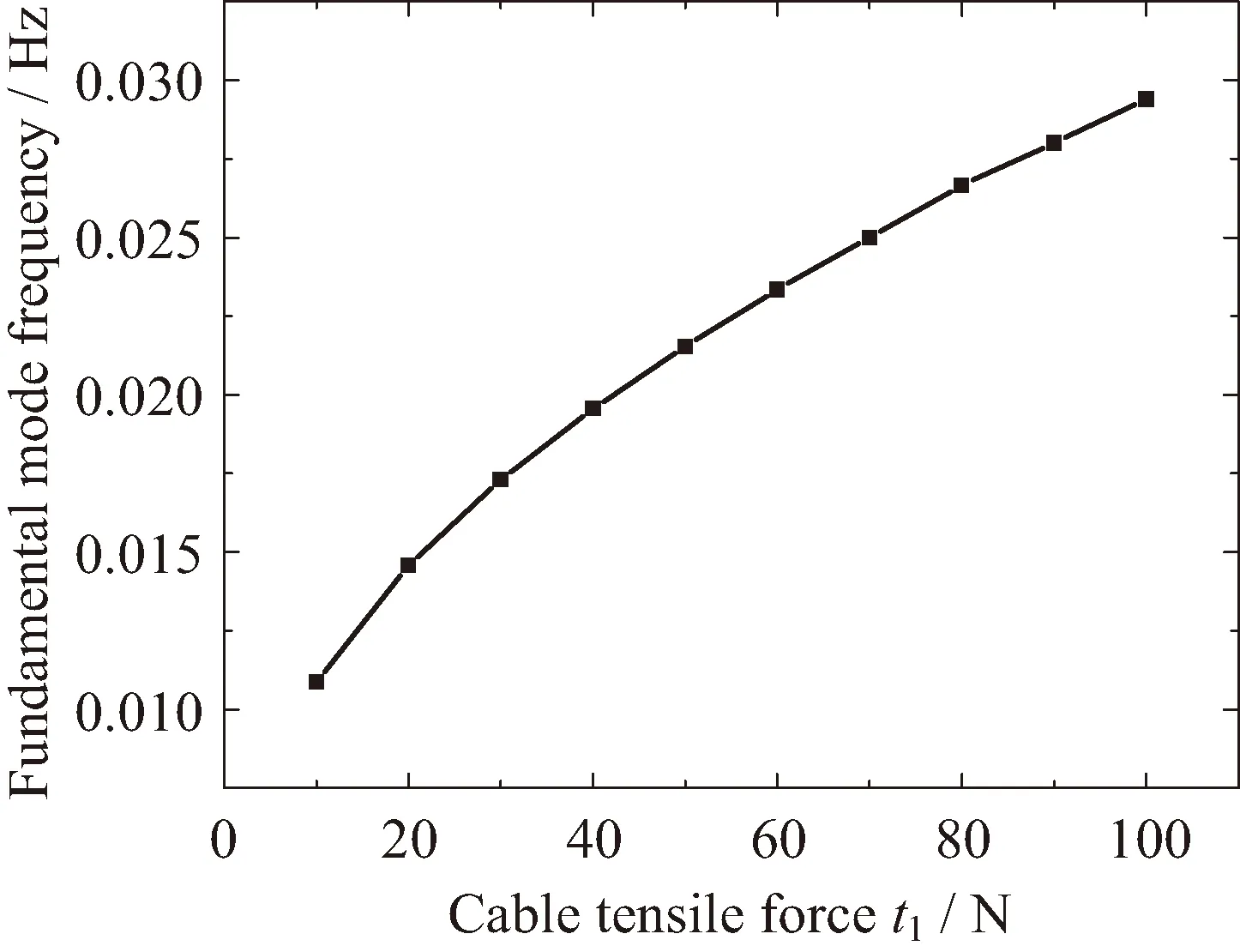
图14 不同绳索张力下50 m口径单层索网天线基频有限元预测结果Fig.14 Fundamental frequency of the 50 m-aperture antenna against the cable tensile force t1

实际情况中，在随机的制造误差的影响下，天线中绳索的张力难以做到绝对轴对称分布。在不对称的绳索拉力作用下，天线环向支撑肋发生屈曲的概率大幅提高。图15中为考虑天线绳索长度误差情况下天线的稳定构型。在天线模型中加入-1%～1%的随机绳索长度误差后，当绳索张力t1=100 N时，在制造误差影响下天线整体产生屈曲变形。虽然提升天线的绳索张力能够有效提升天线的基频，但过高的绳索张力会导致天线发生总体屈曲变形。由于天线总体发生屈曲的临界绳索张力与制造误差相关，并且制造误差的幅值及分布为随机变量，因此难以通过有限元模型精确预测天线总体屈曲的临界绳索拉力。实际情况下，应通过实验确定绳索的临界张力，从而避免天线发生屈曲变形。因此，本文在后续分析中，不失一般性，选取绳索张力t1=50 N。

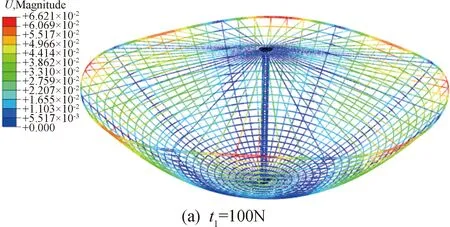
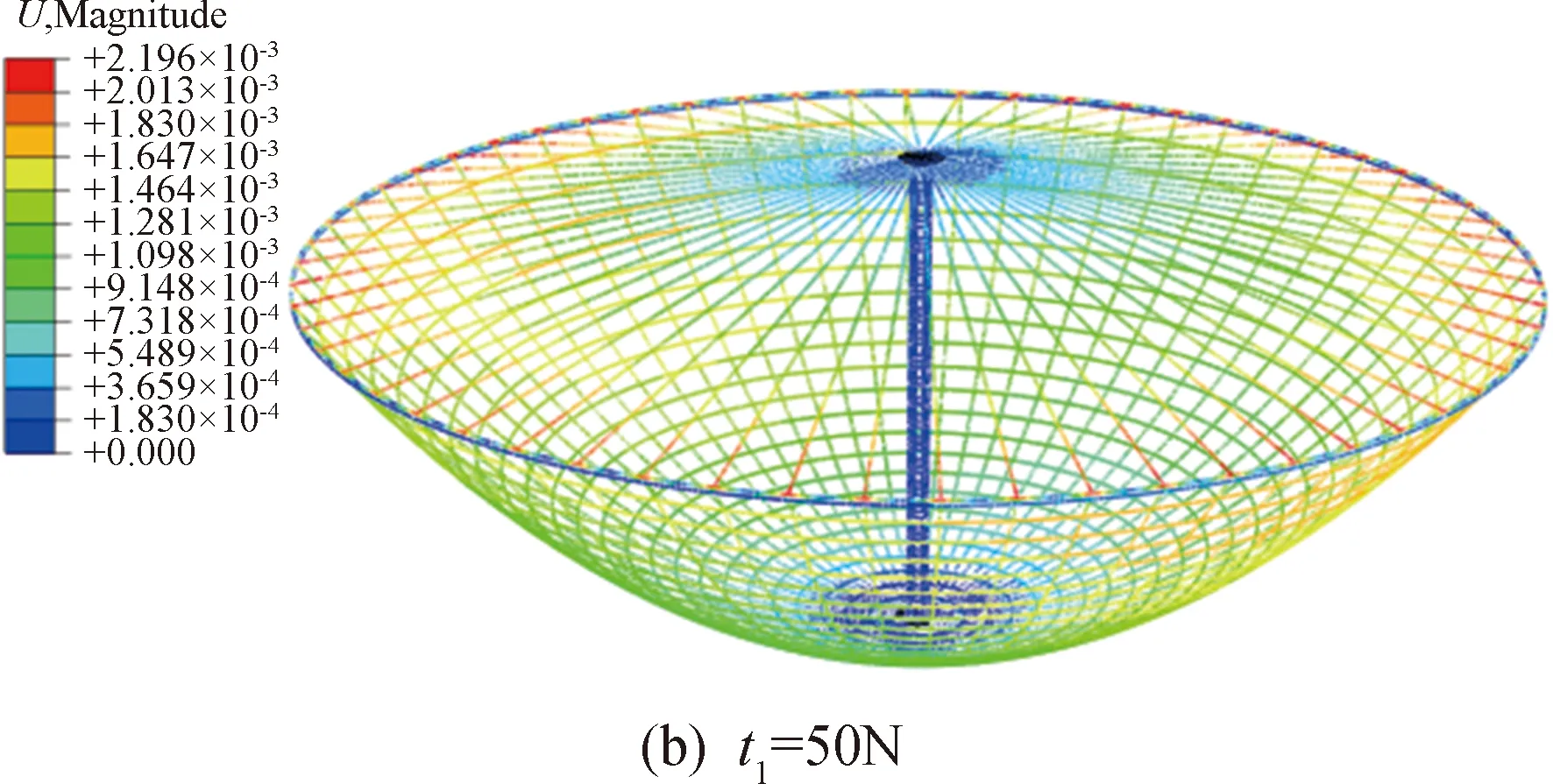
图15 单层索网天线稳定构型及屈曲构型(其中天线绳索引入了-1%～1%的随机误差，放大10倍显示)Fig.15 Static shapes of the one-layer cable-net antenna (the cables in the antenna have random length error ranging from +1%～1%)

3.3 形面精度在轨调整

基于有限元模型，对单层索网的形面精度调整能力进行仿真验证。为了模拟天线在轨热变形，在建立天线的内部张力场后，在第二个静态分析步中对天线模型施加均匀的温度场ΔTuniform=±100℃，并在第三个静态分析步中调整天线中心轴的长度，实现天线反射面形面精度调整。不同均匀温度场下，单层索网天线的形面精度调整过程有限元预测结果如图16所示。有限元分析显示，在-100℃和100℃的均匀温度变化下，天线反射面的形面误差从0.946 mm分别增加至19.33 mm和17.63 mm。当调整天线的中心轴长度后，天线反射面的形面误差将降低至4.4 mm和4.56 mm。

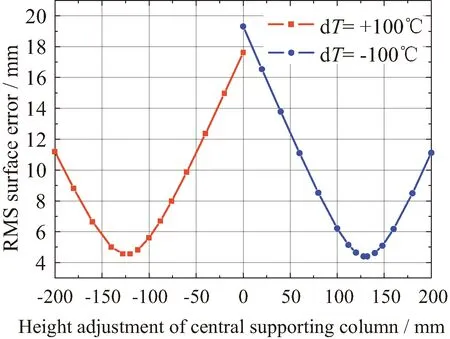
图16 天线形面精度调整过程有限元预测结果Fig.16 Variation of antenna’s surface RMS error against the height adjustment of the central supporting column

天线在轨运行时，其温度通常难以均匀分布。为预测单层索网天线在不均匀温度场下的形面精度特性，本文假设天线索网的温度分布为：

T=200×|sin [θ]|-100

(13)

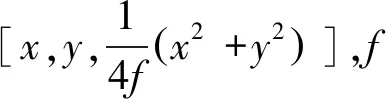
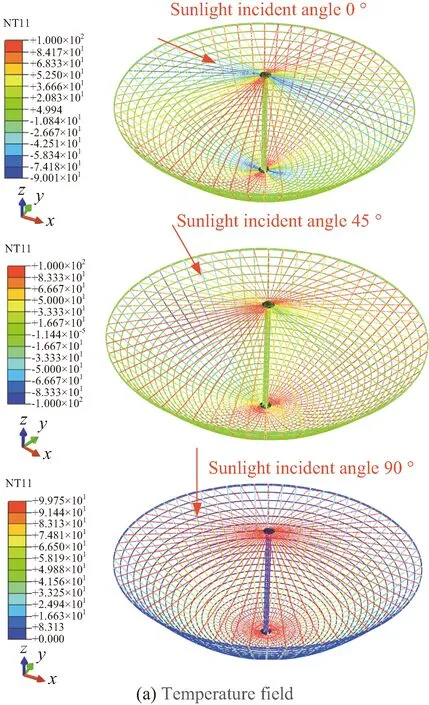
图17 非均匀温度场下单层索网天线的稳定构型(放大20倍显示)Fig.17 Static shapes of the one-layer cable-net antenna with un-uniform temperature fields

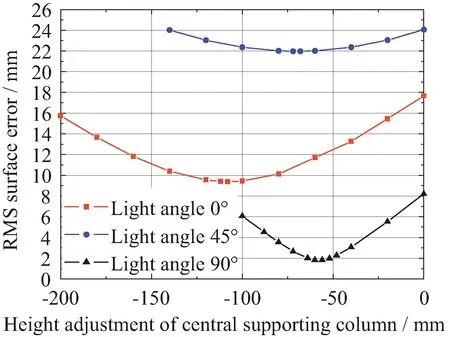
图18 非均匀温度场下天线形面调整过程有限元预测结果Fig.18 Variation of antenna’s surface RMS error against the height adjustment of the central supporting column

4 结论

本文提出了一种新型的单层索网空间可展开天线。单层索网天线反射面由多个环向支撑肋及径向拉索组成。基于静力平衡分析，本文给出了天线反射面中绳索张力及制备长度的计算方法。基于能量法，本文建立了单层索网天线的构型预测理论模型，实现了单层索网天线的找形分析。基于理论模型，证明了可通过调整单层索网天线的中心轴长度，实现单层索网的形面精度在轨调节。

基于单层索网天线找形设计结果，本文建立了单层索网天线的有限元分析模型，并系统分析了绳索张紧力对天线形面精度、基频的影响。为避免天线结构发生屈曲变形，本文最终采用的绳索张力为50 N。有限元分析结果显示，在均匀及非均匀温度场下，单层索网天线均能够通过调整中心轴长度来降低热变形的不利影响，实现天线形面精度的在轨调整。在均匀100℃温差下，50 m口径单层索网天线的形面精度误差将能够从20 mm降低至5 mm以下。