基于星光角距/激光测距的卫星组合导航方法

李代伟，淡鹏，贺波勇，陈玉昌，张银发，石峰

1. 宇航动力学国家重点实验室，西安 710043 2. 西安卫星测控中心，西安 710043

1 引言

天文导航采用自然天体或辐射源作为观测对象，通过一定的导航算法计算获得卫星位置信息，具有隐蔽性好、抗干扰能力强、误差不随时间累积等特点，是航天器除惯性导航手段之外的重要自主导航方式。天文导航通过观察天体获取角度信息，并结合卫星位置的几何关系来确定卫星位置。由于纯角度观测的方法具有严重的非线性，角度测量误差换算到距离误差较大，因而天文导航比卫星导航定位精度至少低一个量级，这极大限制了天文导航的应用[1-3]。

激光测距基于点定位技术，利用飞行器本体装载的激光测距仪器向参考点发射激光波束，通过接收装置接收参考点的反射激光信号，根据发射与接收激光信号的时间差换算二者距离。激光脉冲具有较高的能量，利用时间宽度6 ns的脉冲激光，完全可以获得优于0.1 m的测距精度[4-5]。

激光的载频比微波高3～4个数量级，适合传输大容量的数据。激光的发散角非常小，可达到几个微弧度的量级，能量集中，旁瓣小，方向性好，天线增益高，天线口径小。特别适合应用在对功率、体积以及质量等系统指标要求比较苛刻的场合，例如卫星系统。同时，由于激光抗电磁干扰能力强、保密性好的特点，在卫星测控系统中也大有用武之地[6-8]。

为了进一步提高航天器自主导航精度，国内外开展了天文导航与其他导航方式的组合导航研究，典型方法是天文/惯性组合导航以及其与无线电多普勒测速等测量方式的组合[9-10]。这些组合导航方法极大提高了定位定速精度，但同时也存在惯性器件的长期漂移和无线电易受干扰等问题。本文在天文导航角度观测的基础上，引入激光测距作为新的补充观测量。利用激光测距方法可以直接获得卫星到地面信标的高精度距离量，能够弥补角度间接测量的不足，同时其发散性小，隐蔽性好。但是，激光测距作为导航观测量，需要已知地面特定信标的准确位置，此外，星上激光测距受功耗和气象条件等约束，无法实现较高频率的测量。考虑到地面信标的建立复杂度、星上资源约束以及隐蔽性需求，激光测距主要作为辅助导航系统进行距离观测，与天文导航进行信息融合，从而提高天文导航精度。

2 组合导航系统原理

图1给出了天文/激光组合导航系统的基本方案。天文导航根据恒星星历数据库中恒星和地球数据，采用星敏感器和地平仪分别测量某恒星与地心矢量，从而获取星光角距观测量。激光测距仪根据预置地面信标数据库位置，进行卫星与地面已知信标之间的距离测量获取距离观测量。结合卫星在轨运动模型，进行天文/激光测距导航信息融合，最终获得导航定位信息。

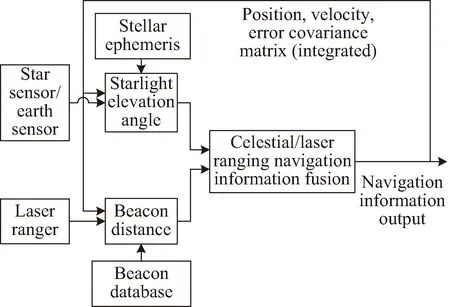
图1 组合导航方案Fig.1 Integrated navigation scheme

(1)

红外地平仪是一种卫星姿态敏感仪器，由光学系统、红外探测器和数据处理电路组成。通过光学系统和探测器敏感地球的红外辐射信息，经数据处理计算获得卫星相对于地球的姿态信息，根据红外地平仪测量原理，可获得地心方向矢量为[11]。

(2)

激光测距仪是利用激光测距技术通过向目标发射激光脉冲而获取卫星到地面信标的距离。卫星激光测距几何关系如图2所示。

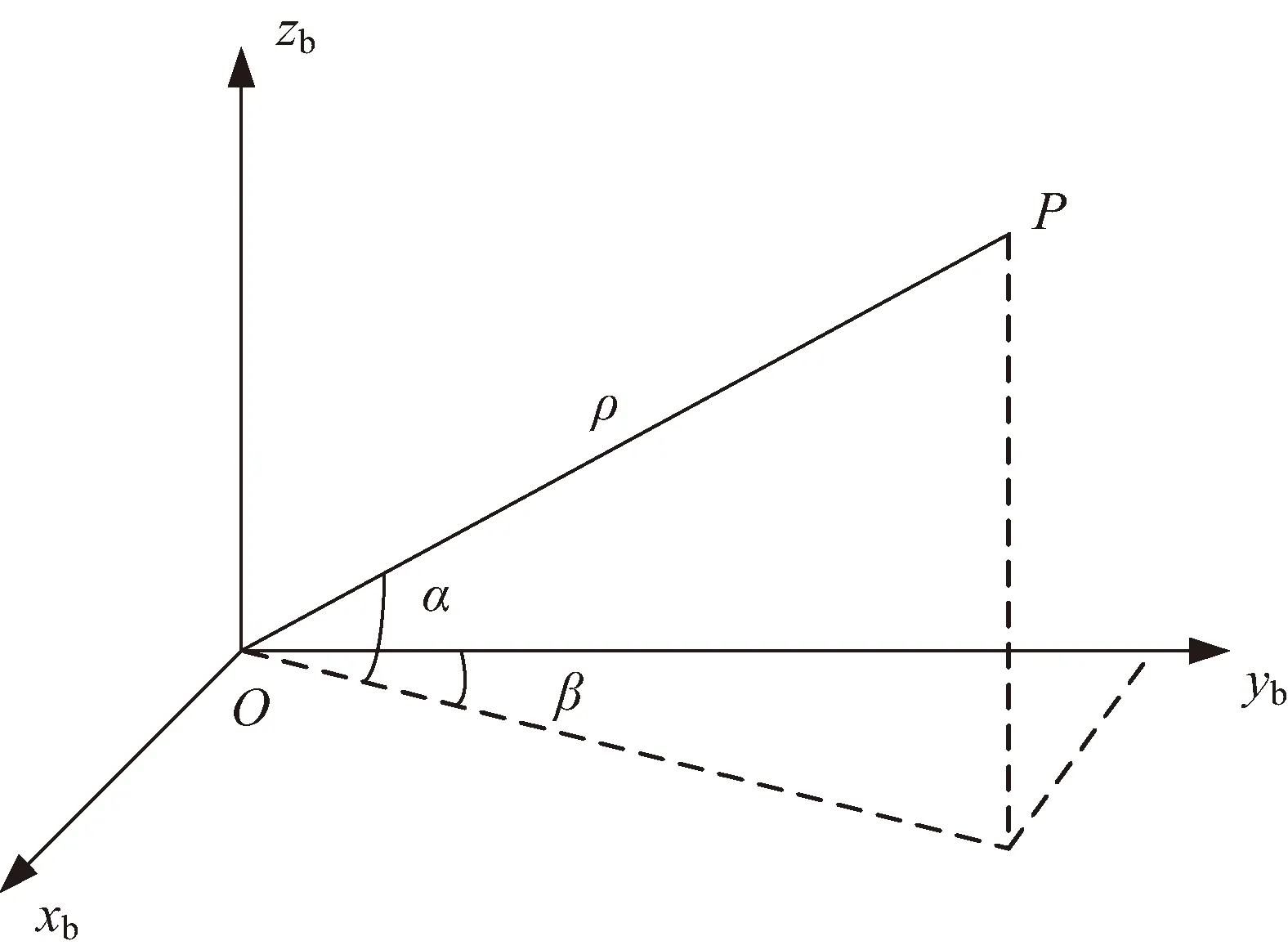
图2 卫星激光测距几何关系Fig.2 Geometric relationship of satellite laser ranging

图2中，O为卫星所在位置，其在J2000地心惯性系下坐标为(x,y,z)，Oxbybzb为卫星本体坐标系，P为地面已知信标位置，其坐标为(x0,y0,z0)，利用激光仪测量卫星O与信标P之间的距离ρ，利用星上角位置测量装置可获取激光方向高低角α和方位角β，于是可获得激光测量的距离、高低角和方位角3个观测量。

3 组合导航系统方程

3.1 轨道动力学方程

利用牛顿二体引力模型建立卫星轨道运动学方程[12]，结合地球非球形引力和其他外部摄动力，建立卫星运动学模型：

(3)

式中：r和v为地心惯性系下卫星的位置、速度矢量；μ为地球引力常数；P(r,v)为受外部摄动力引起的加速度项。利用勒让德多项式将上式展开并化简，则卫星运动状态方程可写为[13-14]:

(4)

式中：r为卫星位置矢量r的模，[x,y,z,vx,vy,vz]为卫星位置、速度在地心惯性坐标轴上的分量；J2为地球引力二阶带谐项系数；ΔFx、ΔFy、ΔFz为地球非球形高阶摄动、日月摄动、太阳光压摄动以及大气摄动等摄动影响。wx,wy,wz为未建模误差，等效为高斯白噪声。

3.2 天文观测方程

基于星敏感器和地平仪观测实现的天文导航原理如图3所示。

图3 天文导航原理Fig.3 Celestial navigation scheme

星光观测矢量由星敏感器观测恒星得到，卫星利用地平仪敏感地平从而计算得到卫星矢径。两者的夹角φ与卫星的空间位置具有明确的函数关系，建立观测方程为：

(5)

式中：s是导航恒星星光单位矢量，根据星历数据库查询得到；va为测量噪声，一般等效为高斯白噪声。

3.3 激光测距观测方程

当信标在可见范围内时，采用星载激光测距仪进行卫星和信标之间测距，此外，根据跟瞄系统输出可以获得信标相对卫星的高低角和方位角信息，可以构建激光测距观测方程：

(6)

式中：vi(i=1,2,3)为测量噪声。

4 信息融合方法

选取卫星位置和速度为状态量，将状态方程(4)进行离散化，选取星光角距、激光测距、信标高低角和方位角为观测量，将观测方程(5)(6)进行离散化，卫星自主导航系统状态方程和观测方程为：

xk+1=f(xk)+wk

(7)

(8)

式中：xk∈RL,为状态向量；yk∈RM,为观测向量；wk～N(0,Qk),为过程噪声；vk～N(0,Rk),为测量噪声，且wk和vk不相关。

可见，该系统具有非线性的形式。为了避免线性化过程引起的二阶系统截断误差，采用UKF滤波方法进行导航解算[15-16]。

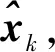
(9)

i=1,…,L

(10)

i=L+1,…,2L

(11)

利用以上变换结果，进行预测计算：

χi,k/k-1=f(χi,k-1)

(12)

(13)

(14)

(15)

(16)

(17)

最后，对状态量和协方差矩阵进行更新，

目前，我国职业经理人市场存在的问题是：职业化程度低、数量少、法律法规体系不健全、企业主和经理人的信任体系没有建立起来、认证和评价体系还没有各方的认可。这就导致企业在选聘职业经理人时获取信息存在问题。

(18)

(19)

(20)

(21)

(22)

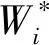
当受地面信标数量限制，或由于大气条件等无法实现激光连续观测时，主要采用天文导航的方式实现自主导航。当卫星能够同时获得星光角距和激光测距信息时，可进行联合观测，考虑到观测量的断续性，采用联邦滤波模式进行两种方式的融合计算[17]。联邦滤波器具体结构如图4所示。局部滤波器1主要利用星光角距测量信息进行UKF滤波实现导航计算，局部滤波器2主要利用激光测量信息进行UKF滤波实现导航计算，然后将各局部滤波器估值在信息融合模块中进行融合计算，最终得到系统状态最优估值。由于联邦滤波器采用二级并行架构，具有设计灵活、容错性好等优点，可满足不同时刻的观测量并行滤波处理要求。

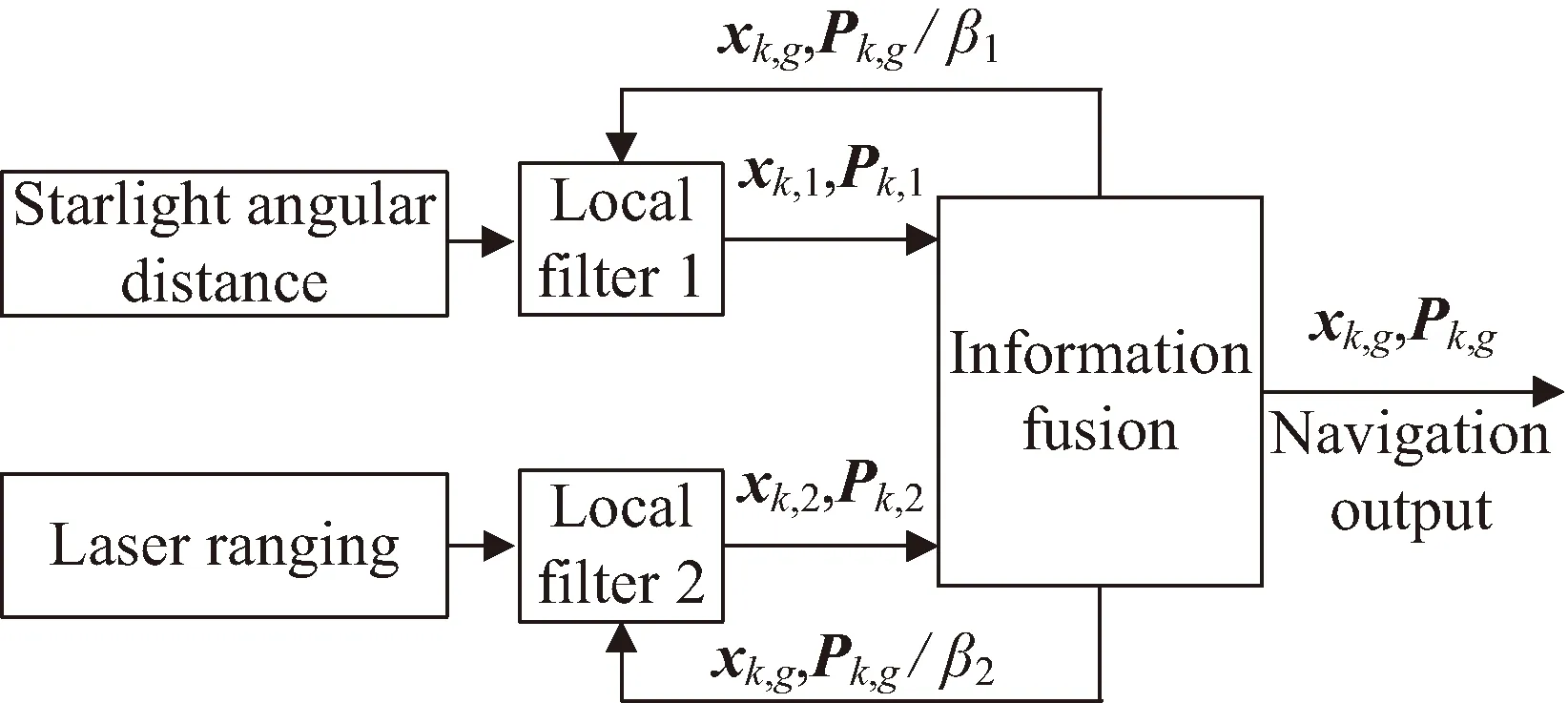
图4 联邦滤波器结构Fig.4 Federated filter architecture

令xk,1,Pk,1为天文导航子滤波器状态估计值及其误差协方差阵，xk,2,Pk,2为激光测距导航子滤波器状态估计值及其误差协方差阵，则导航系统最优状态估计值及其误差协方差阵可进行以下计算：

(23)

(24)

xk,i=xk,g

(25)

(26)

β1+β2=1

(27)

式中：βi(i=1,2)为反馈系数，与各局部滤波器误差协方差阵成反比关系。

5 仿真试验

对天文导航方法和天文/激光测距组合导航方法分别进行仿真分析。设定的卫星轨道根数为：半长轴a=7 136.635 km,轨道倾角i=65°，偏心率e=0.001 809，升交点赤经Ω=30°，近地点幅角ω=30°，星敏感器镜头视场选为20°×20°，姿态确定精度3″，红外地平仪测量精度为0.02°，导航恒星根据在天球中的分布随机选取。激光测距仪测距精度为0.5 m，假设地面信标布局能够保证整个仿真过程的连续可见。星光角距和激光测距观测量周期设为5 s。系统初始参数为：

状态初始估值：位置误差1 000 m，速度误差10 m/s。

系统的过程噪声方差阵：

星光角距观测噪声方差：Rak=1×10-6。

激光测距观测方程方差：

首先，对仅用星光角距观测的天文导航方法进行仿真，考察其导航精度。然后，对天文/激光组合导航模式进行仿真验证，又分为两种模式：模式一，假设导航全过程激光测量完全可用；模式二，考虑实际应用场景，在天文导航的过程中引入激光测量实现组合导航。

(1)天文导航

以星光角距为观测量，进行UKF滤波计算，天文导航位置和速度估计误差分别如图5、图6所示。

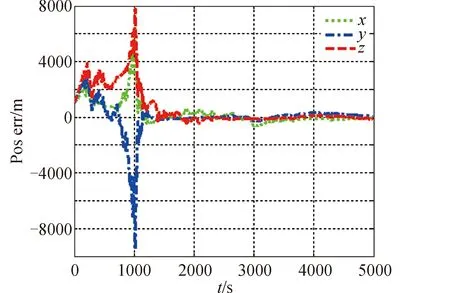
图5 天文导航位置估计误差Fig.5 Position estimation error of celestial navigation

图6 天文导航速度估计误差Fig.6 Velocity estimation error of celestial navigation

开展100次蒙特卡罗仿真并进行误差统计，天文导航位置、速度估计均方根(RMS)误差如表1所示。

表1 天文导航均方根误差

(2)组合导航

模式一：以星光角距和激光测量为观测量，进行UKF滤波计算，天文/激光测量组合导航位置和速度估计误差分别如图7和图8所示。

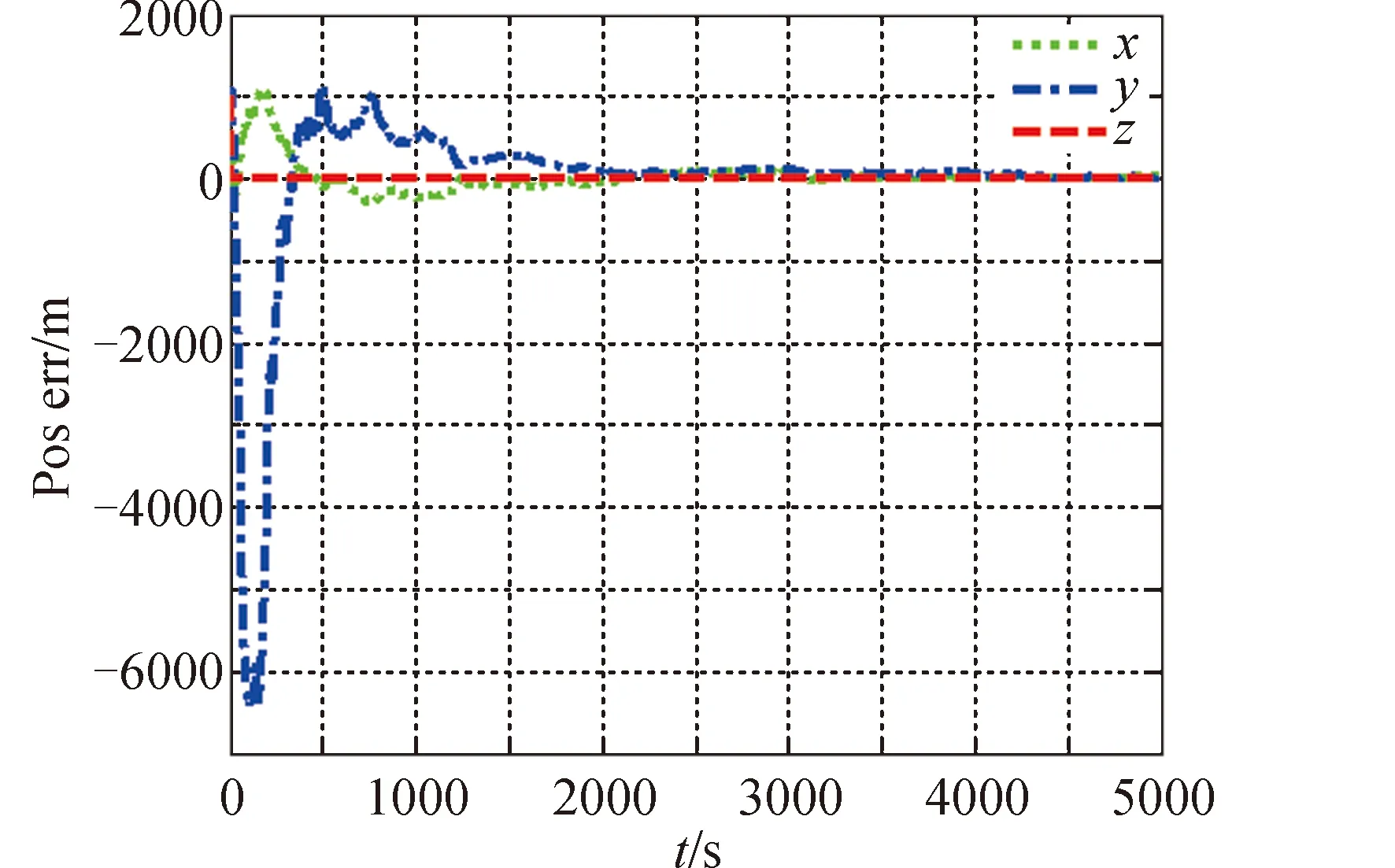
图7 天文/激光测距导航位置估计误差Fig.7 Position estimation error of celestial/laser navigation

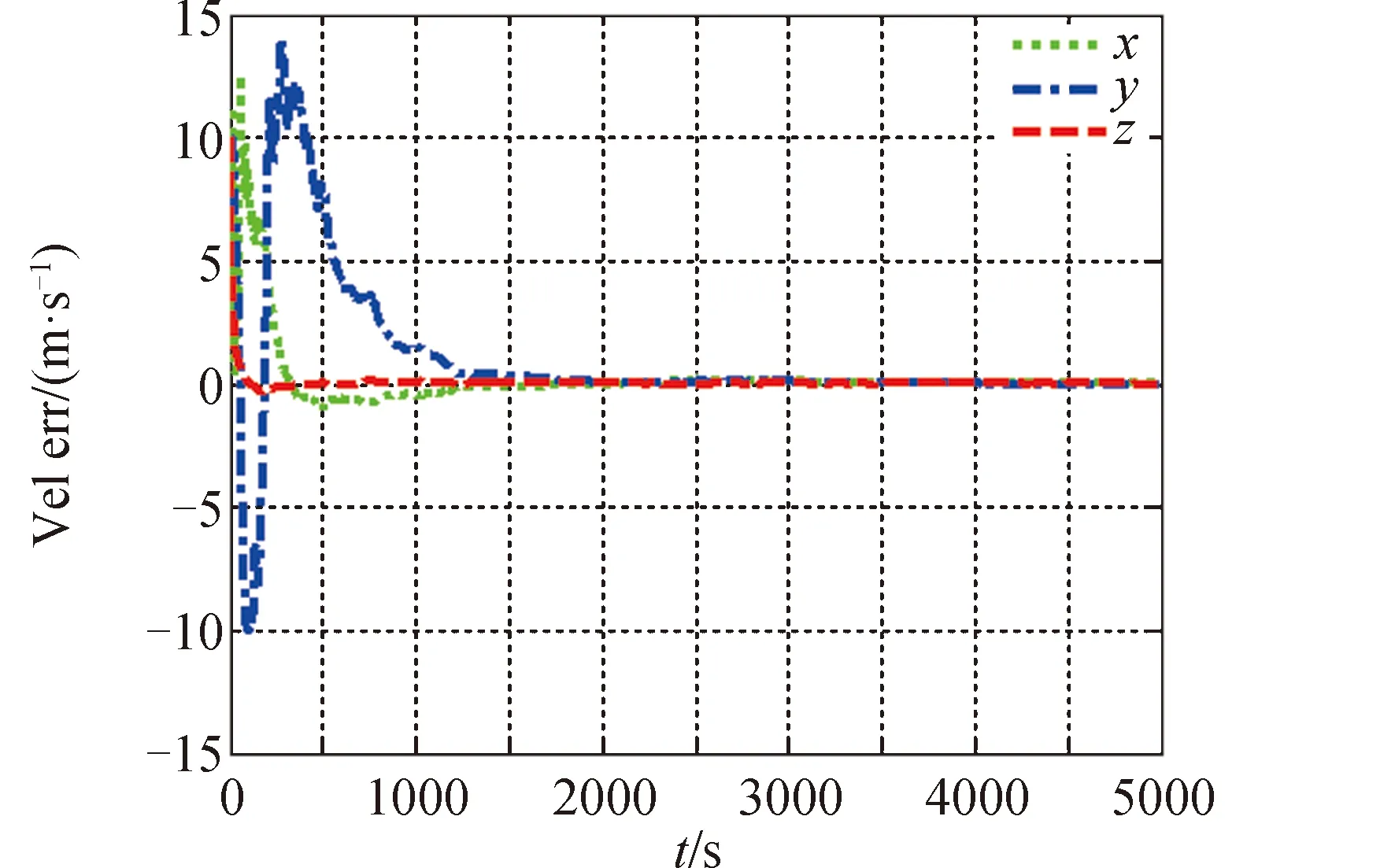
图8 天文/激光测距导航速度估计误差Fig.8 Velocity estimation error of celestial/laser navigation

开展100次蒙特卡罗仿真并进行误差统计，天文/激光组合导航方法位置、速度估计均方根误差如表2所示。

表2 组合导航均方根误差

模式二：首先以星光角距为观测量，进行天文导航计算，在2 500 s后，加入激光测量实现组合导航，位置和速度估计误差分别如图9、图10所示。

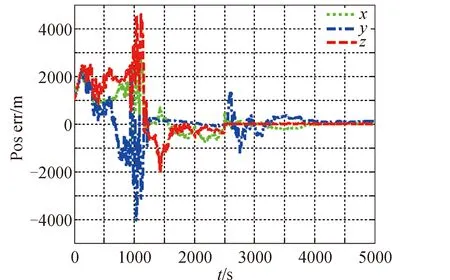
图9 天文/激光测距导航位置估计误差Fig.9 Position estimation error of celestial navigation

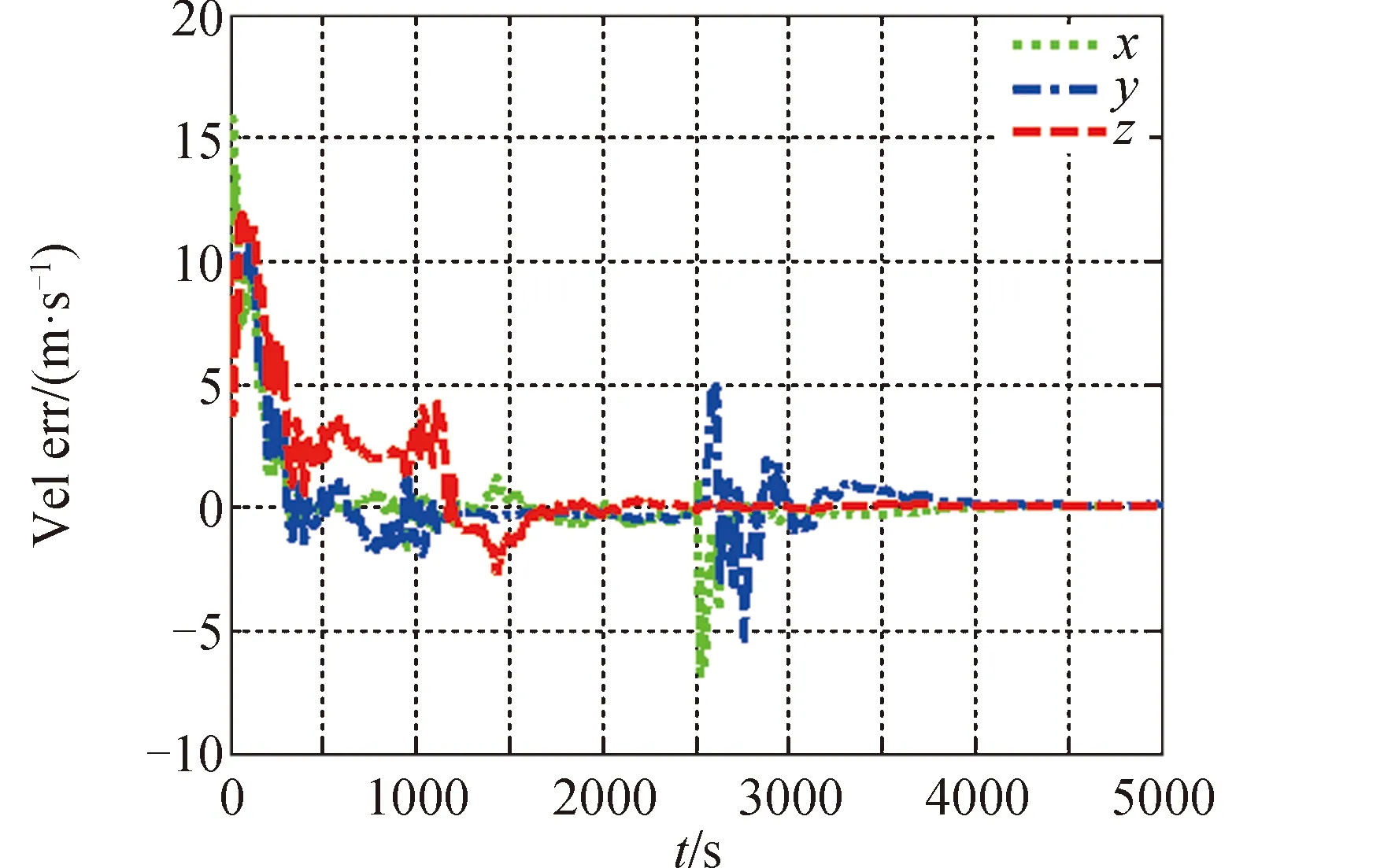
图10 天文/激光测距导航速度估计误差Fig.10 Velocity estimation error of celestial navigation

开展100次蒙特卡罗仿真并进行误差统计，两种方法的导航位置、速度估计均方根误差如表3所示。

表3 均方根误差

通过仿真可知，单纯采用天文导航时，自主导航位置精度为百米量级，而采用激光测距辅助时，自主导航定位精度提高到十米量级，速度精度也提高一个量级。从滤波过程看，天文导航和组合导航方式在滤波初期都有较大的误差波动，该现象主要来自于观测量与被测状态的几何特性以及滤波器参数等因素影响。单纯的天文导航由于只有角度观测，存在极大的非线性度，滤波收敛时间慢，数据存在一定的波动性，而激光测距辅助引入了直接距离量测，滤波收敛速度和稳定性都得到了明显改善。在天文导航过程中，当激光测量信息可用时，可以实现天文/激光组合导航。由于新的观测信息的引入，组合导航滤波器在初始阶段存在一个小幅波动过程，考虑实际应用，在该过程中应以天文导航估计输出为主，当组合导航滤波器稳定后，滤波器输出切换为组合导航输出模式。

6 结论

本文以实现卫星高精度自主导航为目的，在传统天文导航的基础上，提出了以激光测距手段进行组合导航的方法。通过星载激光器对地面已知信标点的直接测量，为纯角度观测量天文导航提供高精度直接距离测量，通过设计联邦卡尔曼滤波器，对二者进行数据融合。仿真结果表明，通过引入激光测距观测信息，自主导航位置和速度精度有明显的提高，滤波器能够实现平稳的高精度导航信息输出。