星载天线反射面型面热变形影响因素分析

张正尧，江世臣，王 萌，胡梦遥

（上海卫星工程研究所，上海 201109）

0 引言

卫星在轨运行时会周期性进入阴影与光照区，环境温度亦随之周期性变化，最大温差可达200 ℃，将导致卫星结构热变形，影响卫星的功能性能。例如，星载天线对变形敏感，热变形会造成型面误差，影响天线增益[1]。随着航天任务对天线分辨率要求的不断提高，对于大口径天线的需求也越来越迫切，但天线口径的增大同时要求天线反射面具有更高的型面精度[2]。因此，尽量减小由于热变形导致的天线反射面型面误差是大口径天线设计中的关键。

星载天线结构设计主要包括材料选取、主反射面结构设计和支撑结构设计。现有星载天线反射面材料主要有低膨胀微晶玻璃材料、铝铍等金属材料、碳纤维复合材料和碳化硅等[3-5]。研究人员对多种材料的天线反射面进行了热变形分析及设计，包括：各因素对天线反射面型面变形的影响分析[1-3,6-8]；采用热光学分析方法分析径向、轴向及周向温度梯度对反射面成像质量的影响[9]；星载抛物面天线在轨运行时各位置各时刻的热变形情况分析[10-12]。

在天线结构设计中，由于天线为抛物面且具有支撑结构，边界条件复杂，采用理论方法分析其热变形较为困难；而采用试验方法则成本较高、周期较长，且难以分析天线结构参数对热变形的影响，故多采用仿真方法分析天线热变形。但由于许多研究人员对天线反射面热变形进行仿真分析时将热膨胀系数（CTE）视作常值，而实际材料的热膨胀系数是随温度变化的，导致分析结果存在误差。

为了分析热膨胀系数随温度变化对天线热变形分析的影响，并指导天线材料选取以及厚度和支撑位置设计，本文针对简化抛物面天线模型，采用仿真方法对各工况及结构参数下的天线反射面进行热变形分析。

1 天线反射面型面误差计算

天线增益是评价天线性能的重要参数，而天线型面变形导致的型面误差会带来增益损耗，因此在天线反射面设计时应着眼于尽量减小反射面的型面变形。采用天线反射面型面误差的方均根（RMS）值作为反射面变形的评价指标。在型面误差计算时，应先对变形后的反射面进行拟合，再计算实际反射面对拟合反射面的型面误差RMS值，如图1[13]所示。

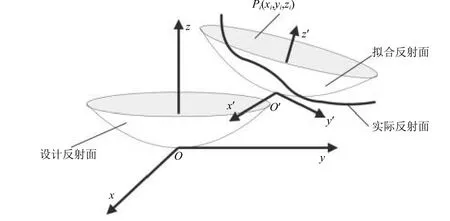
图 1 天线反射面型面误差计算示意Fig. 1 Schematic diagram of antenna reflector surface error calculation

天线反射面为抛物面，在坐标系Oxyz下，设计反射面方程为

其中f为焦距。

对变形后的天线反射面进行拟合，定义新坐标系O′x′y′z′，拟合反射面在新坐标系下任一点坐标为(x′,y′,z′)，焦距变化量为Δf，新坐标系下拟合反射面方程为

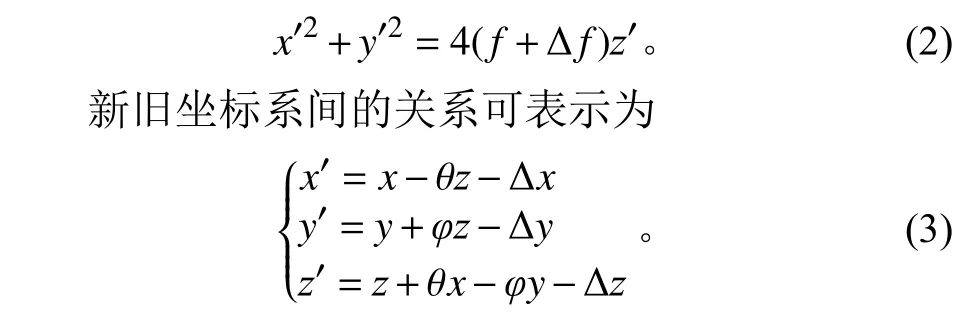
式中：(Δx, Δy, Δz)为O′在Oxyz坐标系下的坐标；φ和θ为坐标系Oxyz按xy顺序变换到坐标系O′x′y′z′的欧拉角。

将式(3)代入式(2)，可得拟合反射面在Oxyz坐标系下的表达式

通过推导，可得实际反射面上一点Pi(xi,yi,zi)到拟合反射面的距离为

其中(Δxi, Δyi, Δzi)是Pi(xi,yi,zi)相对于原坐标的变形量。

对于所有n个表面节点，各点到拟合反射面的距离的平方和为根据最小二乘法定义，可确定拟合反射面参数(Δx,Δy, Δz,φ,θ, Δf)，

将这些参数代入式(5)可得所有节点到拟合反射面的距离，则反射面型面误差RMS 值为

2 热膨胀系数随温度变化对热变形仿真影响

2.1 热膨胀系数

材料在温度变化时会发生热变形，这种特性可用材料的热膨胀系数来描述。热膨胀系数的表述主要包括平均热膨胀系数α和瞬时热膨胀系数αi，对于如图2 所示的膨胀曲线，其平均热膨胀系数可表示为

图 2 膨胀曲线Fig. 2 Expansion curve

仿真分析时通常采用平均热膨胀系数，而实验测得的通常是材料的瞬时热膨胀系数，故在仿真时需要利用式(11)将实测的瞬时热膨胀系数转换为各特征温度下的平均热膨胀系数，再输入仿真软件作为材料随温度变化的热膨胀系数。

2.2 考虑热膨胀系数随温度变化对热变形仿真影响分析

在工程问题的仿真中，往往选取材料在常温下的特征值作为相应仿真材料参数，但材料参数在不同温度下会发生变化，这对于仿真工况不在常温的工程问题就会带来误差。材料弹性模量、泊松比等参数在不同温度下变化较小，视其为常值进行仿真所带来的误差尚在可以接受的范围内；但对于某些材料，其热膨胀系数随温度变化明显，如果在设计中依然视其为常值，则会给热变形仿真分析带来误差。本文选取2 种天线反射面常用材料——ULE 玻璃和M55 碳纤维层合板（M55 层合板），分析考虑热膨胀系数随温度变化与否对热变形仿真的影响。表1 给出这2 种材料在25 ℃下的材料参数，ULE玻璃的材料参数取自康宁公司产品手册[14]，M55 层合板的材料参数取自实测结果[8]，其中：E1为板面内各方向弹性模量；E3为垂直板面方向弹性模量；ν12为板面内泊松比；G12为板面内方向剪切模量；G23为垂直板面各方向剪切模量；α11为板面内各方向热膨胀系数；α33为垂直板面方向热膨胀系数。

表 1 ULE 玻璃和M55 层合板在25 ℃下的材料参数Table 1 Material parameters of ULE and M55 laminate at 25 ℃

ULE 玻璃瞬时热膨胀系数随温度变化曲线如图3 所示。

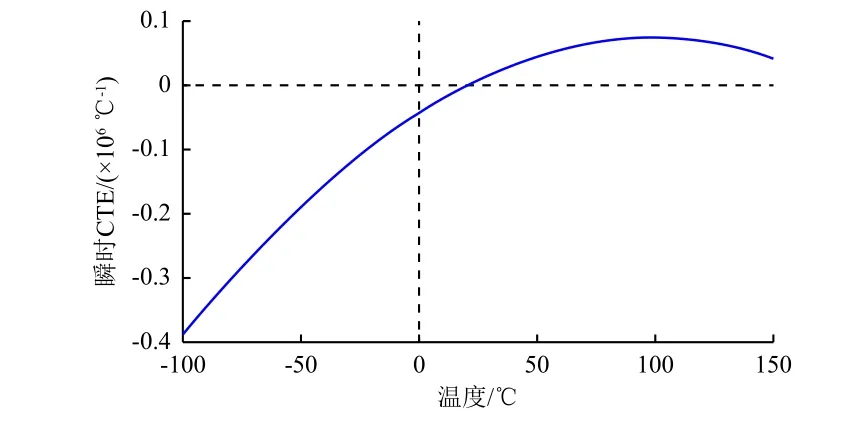
图 3 ULE 玻璃瞬时热膨胀系数变化曲线Fig. 3 Instantaneous thermal expansion coefficient curve of ULE glass

M55 层合板采用了正交铺层，故在面内准各向同性，而垂直面方向与沿面方向热物性参数差异较大。实测的准各向同性正交铺层M55 层合板瞬时热膨胀系数随温度变化曲线[8]如图4 所示。

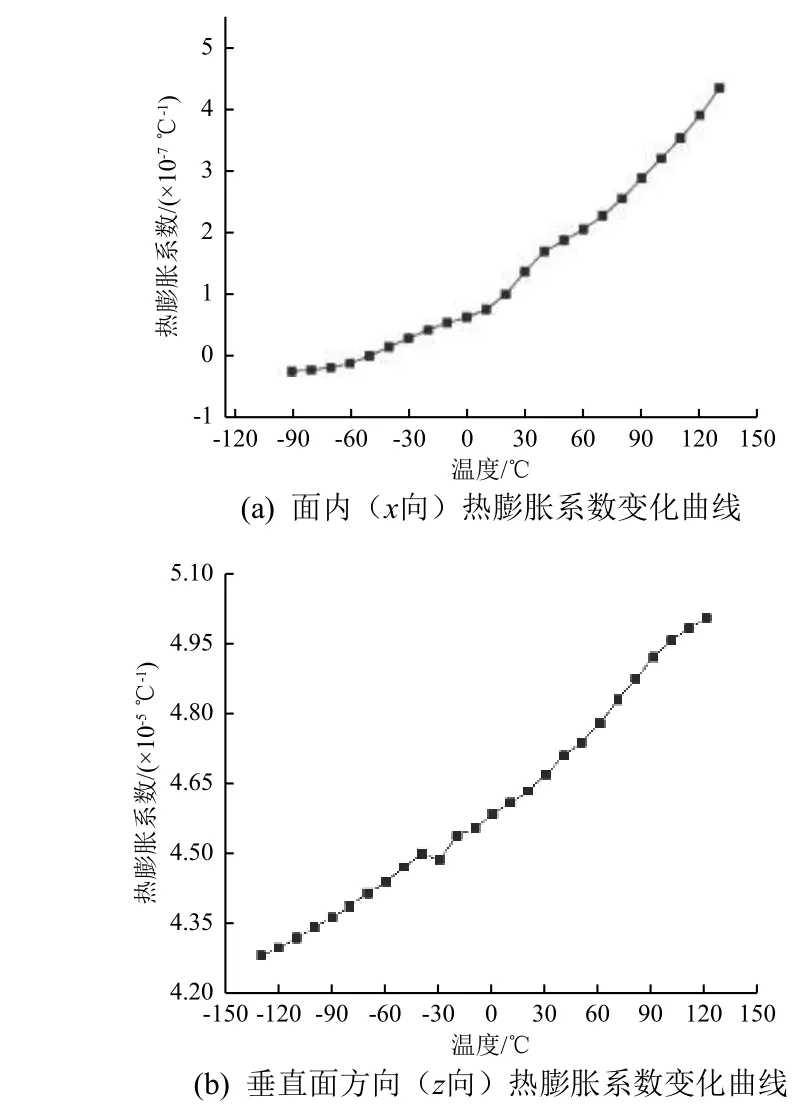
图 4 M55 层合板瞬时热膨胀系数变化曲线Fig. 4 Instantaneous thermal expansion coefficient curve of M55 laminate

本文以抛物面天线反射面为研究对象，其半径500 mm、厚度60 mm、焦距2 m。为分析天线反射面不同温度下的变形情况，利用Abaqus 软件建立有限元模型（如图5(a)所示），其材料参数设置参考表1，各温度下材料热膨胀系数通过瞬时热膨胀系数利用式(11)转换得到；单元采用8 节点实体单元，为充分考虑反射面厚度方向变形，设单元尺度为20 mm。设置模型约束为如图5(b)所示的反射面支撑约束，模型载荷为均匀温度场。

图 5 抛物面天线反射面Fig. 5 Paraboloidal antenna reflector

考虑热膨胀系数（CTE）随温度变化或CTE取常值时，ULE 玻璃和M55 层合板反射面的热变形（包括中心轴向和径向变形）情况分别如图6和图7 所示，其中形变值为正表示膨胀，为负表示收缩。

图 6 ULE 玻璃反射面热变形曲线Fig. 6 Thermal deformation of ULE reflector

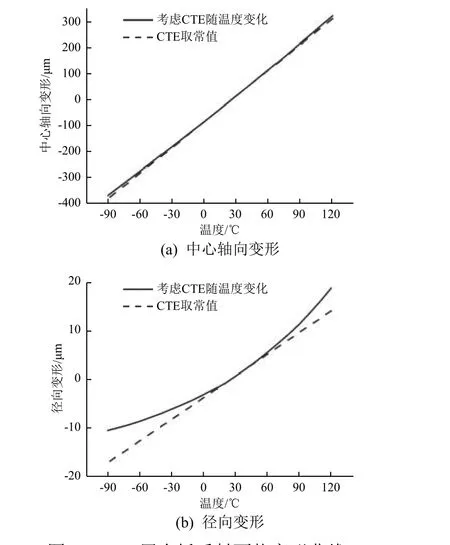
图 7 M55 层合板反射面热变形曲线Fig. 7 Thermal deformation of M55 laminate reflector

由图6 和图7 可以看出，不考虑CTE 随温度变化导致的热变形曲线偏差随着温度变化的增大而逐渐增大。2 种材料在特征温度下各方向最大形变量及其考虑CTE 随温度变化与否的相对偏差如表2 所示：不考虑CTE 随温度变化时，M55 层合板反射面中心轴向变形的相对偏差小于5%；其他条件下的相对偏差均不在可接受的范围内。

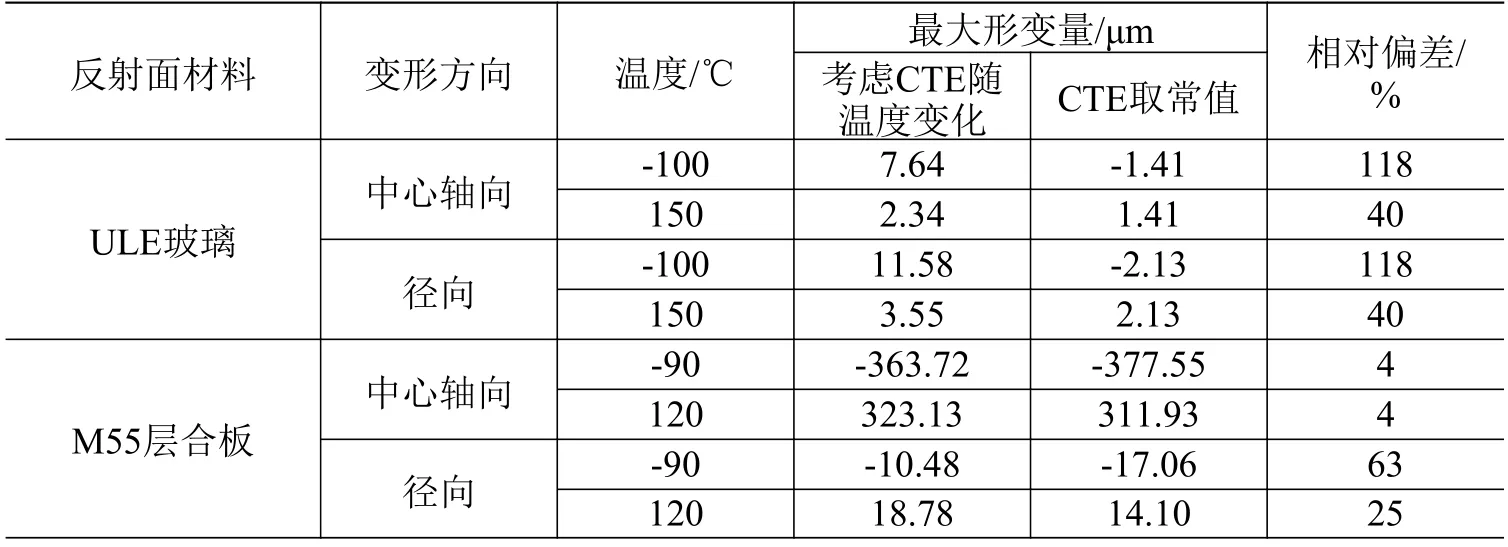
表 2 反射面热变形情况Table 2 Thermal deformation of two kinds of reflectors

利用式(8)计算2 种材料反射面在不同温度下的型面误差RMS 值，其随温度变化曲线如图8 和图9 所示。

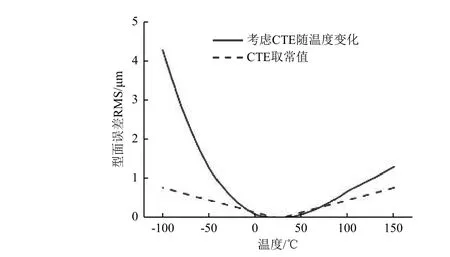
图 8 ULE 玻璃反射面热变形型面误差曲线Fig. 8 Profile error of ULE reflector

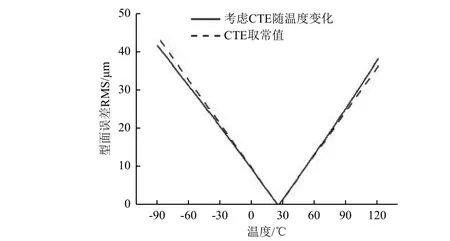
图 9 M55 层合板反射面热变形型面误差曲线Fig. 9 Profile error of M55 laminate reflector

由图8 和图9 可以看出，不考虑CTE 随温度变导致的反射面热变形型面误差曲线偏差也随着温度变化的增大而增大。2 种材料反射面各条件下型面误差RMS 值及其考虑CTE 随温度变化与否的相对偏差如表3 所示：不考虑CTE 随温度变化给反射面型面误差仿真结果的准确性带来影响，对于ULE 玻璃材料，带来的相对偏差较大，不可忽略；对于M55 层合板材料，相对偏差也会超过5%。

综上，ULE 玻璃及M55 层合板面内方向CTE随温度变化明显，不考虑CTE 随温度变化在相应方向上带来的仿真误差均较大，不可忽略；即使对于CTE 随温度变化较小的材料，当温度变化较大时也会对仿真结果产生影响。因此，分析材料结构热变形问题时，为了保证仿真及设计结果的准确性，须考虑材料CTE 随温度的变化。本文后面的分析中，均考虑CTE 随温度的变化。

表 3 反射面型面变形情况Table 3 Deformation of reflecting surface

3 天线反射面型面热变形影响因素分析

天线反射面热变形导致的型面误差与反射面所用材料特性、反射面结构参数等很多因素相关，为减小型面误差，本章研究支撑位置、反射面厚度、选用材料等因素对天线反射面型面热变形的影响。对于确定材料其CTE 随温度变化曲线确定，故本章不再单独分析CTE 变化对型面热变形的影响。

3.1 天线支撑位置对型面热变形影响

支撑是天线结构的重要组成，也会影响天线热变形，为分析天线支撑位置对天线反射面热变形的影响，对相同温度下不同支撑约束位置的反射面进行热变形仿真分析，共设置5 组约束位置（参见图10）。

图 10 不同位置支撑约束设置Fig. 10 Settings of positions for support constraint

反射面材料选用ULE 玻璃，初始温度25 ℃，特征温度-100、150 ℃下的反射面型面误差RMS值与支撑约束位置关系如图11 所示。

图 11 不同约束位置下ULE 玻璃反射面型面误差Fig. 11 Profile error of ULE glass reflector with constraint at different positions

由图11 可见，随着支撑约束逐渐远离中心，反射面型面误差先增大后减小，在距中心300 mm 左右位置达到最大。为了理解这种变化，可将反射面分为反射面中心到支撑位置的内部区域和支撑位置到反射面边缘的外部区域两部分来考虑：热变形时内部区域受约束作用发生弯曲变形，而外部区域可近似为自由变形；反射面整体膨胀时，内部区域变形上凸，导致外部区域向下翻折，两部分变形与抛物面面型相反，带来型面误差；支撑位置变化同时改变两部分热变形，导致型面误差随支撑位置变化的非线性特性。当支撑约束在中心时，反射面整体近似自由热变形，反射面变形与抛物面面型接近，反射面弯曲较小，型面误差RMS 值小于0.1 μm；而当约束靠近边缘时，外部向下翻折的变形减小，反射面整体变形相对符合抛物面面型，型面误差减小。在实际设计中，还需综合考虑支撑位置对天线整体刚度和模态的影响进行优化。

3.2 反射面厚度对型面热变形影响

为了研究反射面厚度对天线反射面热变形的影响，对不同厚度的反射面进行热变形仿真，其中反射面材料分别选用ULE 玻璃和M55 层合板，约束条件如图5(b)所示，初始温度为25 ℃，各特征温度下反射面型面误差RMS 值与反射面厚度关系如图12 和图13 所示。

由图12 可见，对于ULE 玻璃材料，随着反射面厚度的增加，相同温度下反射面型面误差先略有增大再减小，但整体呈随反射面厚度增加而减小的趋势。其原因是，反射面热变形导致的型面误差主要是由上、下表面膨胀程度不同导致的，上表面近似自由热变形，下表面受支撑约束影响热变形受限，在反射面内部产生弯矩，使反射面弯曲产生型面误差；反射面厚度增加会增大反射面内部弯矩，也会使反射面弯曲刚度增大，而随着厚度增加，弯曲刚度变化对反射面变形的影响占据主要，使型面误差总体结果减小。设计中可以适当增加反射面厚度以减小型面误差，但是反射面厚度的增加也会显著增大天线质量，因此不能为了减小型面误差而单方面地增加反射面厚度。

图 12 不同厚度ULE 玻璃反射面型面误差Fig. 12 Profile error of ULE glass reflector with different thicknesses

由图13 可见，对于M55 层合板材料，随着反射面厚度增加，反射面型面误差也在增大。其原因是，对于碳纤维层合板，其横向CTE 远大于纵向的，当反射面过厚时会带来严重的尺度效应，即反射面的热变形型面误差主要由横向变形导致，而不是由弯矩导致的弯曲。在实际应用中不会直接采用过厚的碳纤维层合板作为天线反射面，而是采用蜂窝夹层等结构以保证型面精度。

图 13 不同厚度M55 层合板反射面型面误差Fig. 13 Profile error of M55 laminate reflector against thickneses

3.3 不同材料对型面热变形影响

不同材料在不同温度下的热膨胀系数不同，故反射面采用不同材料其型面变形情况也不同。本节分析不同材料反射面在不同特征温度下的型面变形情况。通过3.2 节分析可知，M55 层合板反射面型面误差受横向变形尺度效应影响较大，且过厚的M55 层合板反射面不具有工程意义，为减小上述因素对选材分析的影响，本节分析中反射面统一设置为厚度2.5 mm、半径500 mm、焦距2 m，初始温度25 ℃，反射面径向热变形及型面误差RMS 值随温度变化情况如图14 和表4 所示。

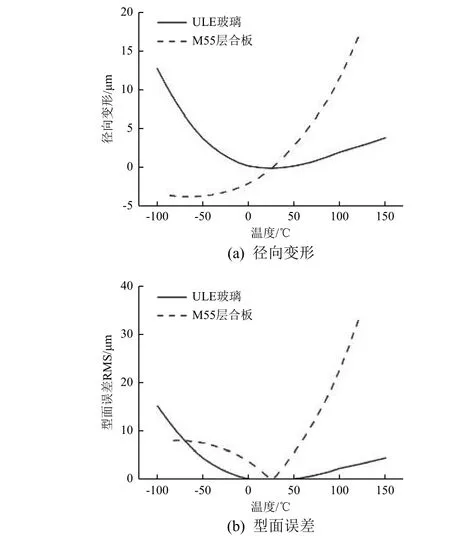
图 14 不同材料反射面热变形及型面误差Fig. 14 Thermal deformation and profile error of reflector made of different materials

表 4 不同材料反射面变形情况Table 4 Deformation of reflector of different materials

由图14(a)可以发现，初始温度25 ℃条件下，ULE 玻璃反射面不论在低温还是高温区间变形均表现为膨胀，而M55 层合板反射面则是低温收缩、高温膨胀。这意味着反射面在轨承受周期性温度变化时，ULE 玻璃反射面将始终承受压应力，而M55层合板反射面将承受周期性的拉/压应力，可能会导致材料产生疲劳效应。由图14(b)及表4 可以看出：对于抛物面天线反射面，在高温区间，ULE 玻璃反射面具有更好的型面精度，其型面误差RMS 值较M55 层合板反射面小1 个数量级；而在低温区间，2 种材料热变形性能接近，在较低温度时M55层合板更具优势。

由于RMS 值算法问题，由负向形变导致的型面误差也体现为正值，对径向变形取绝对值后可以观察到其与反射面型面误差具有较强的相关性，故可以尝试通过减小反射面径向变形来减小反射面热变形型面误差。

3.4 天线反射面综合设计

基于3.1～3.3 节对天线反射面热变形影响因素的分析，本文采用上述2 种材料，提出较优的反射面设计方案，并与初始方案进行比较。各方案设计参数及初始温度25 ℃下的型面误差见表5。

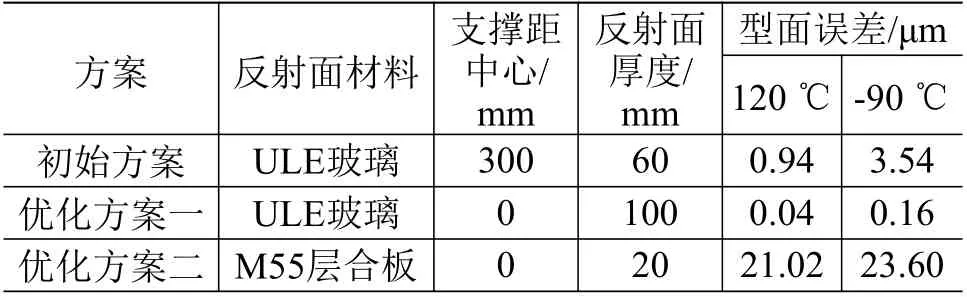
表 5 反射面设计方案比较Table 5 Comparison of reflector designs

由表5 可知：直接采用M55 层合板作为天线反射面材料，其热变形导致的型面误差远大于ULE玻璃反射面，实际方案中可采用M55 层合板为蒙皮的碳蜂窝夹层结构，降低其横向热变形并提高其弯曲刚度，从而减小型面误差；反射面优化方案一较初始方案型面误差减小接近1 个数量级，但其质量会较大，在实际工程中还需对ULE 玻璃反射面进行轻量化设计以满足工程应用需求。

4 结论

本文研究了多种因素对星载天线反射面热变形的影响，主要结论如下：

1）对于材料热膨胀系数随温度变化明显或工作在较大温度范围内的结构，进行热变形分析时，须考虑温度变化对其材料热膨胀系数的影响——如果视热膨胀系数为常值，可能会给分析结果带来较大误差。如果其他材料参数也随温度变化明显，亦应分析它们随温度变化对结构热变形的影响。

2）对于抛物面天线，支撑约束在中间位置时反射面型面误差最小，最优支撑位置需综合考虑反射面刚度、模态等约束进行优化设计。对于ULE 玻璃等各向同性材料，均温下抛物面天线反射面热变形产生型面误差主要是由于受支撑约束限制，上、下表面变形程度不同导致反射面弯曲，型面误差RMS值随反射面厚度增加先增大后减小，并且随弯曲刚度增大整体呈减小趋势。对于M55 层合板等横向热膨胀系数远大于纵向热膨胀系数的碳纤维复合材料，反射面厚度较大时会产生尺度效应——反射面型面精度主要受材料横向变形影响，不能通过增加厚度来减小型面误差。

3）对于星载天线反射面材料的选取，高温区间ULE 玻璃较M55 层合板型面误差小1 个数量级，低温区间两者热变形特性接近，并且在较低温时M55 层合板型面误差更小。在轨周期性温度变化下，M55 层合板材料可能会因热变形产生疲劳效应，而ULE 玻璃材料不存在类似问题。

本文仅就天线反射面热变形讨论了材料选取，未考虑质量及刚度特性要求，实际工程中需综合考虑各项因素。