基于三维点云重建的助推器位姿估计
2022-07-21肖爱群姜鸿翔
肖爱群,姜鸿翔
1. 北京宇航系统工程研究所,北京 100076 2. 北京航空航天大学 宇航学院,北京 100191
1 引言
随着航天技术的发展,依托于运载火箭的各类航天项目,如对月球采样、火星软着陆巡视等不断开展了规划实施。由于航天发射具有高风险性,有必要在火箭发射的各个环节监控其运动状态的变化。助推器分离是运载火箭发射的重要动作之一,精准测量助推器的位姿变化是分析其动力学特性的依据,这对于监测发射过程的异常现象、开展助推器分离装置设计任务、提升火箭发射的成功率与稳定性都有着重要意义。
常用的位姿测算技术包括激光雷达、单目视觉、双目视觉等[1],例如赵高鹏等基于激光成像雷达对自由翻滚运动状态下的火箭箭体进行了运动参数的估计[2]。魏亮设计了基于特征点云的双目视觉位姿测量方案[3],获取了火箭喷管的位姿信息。高燕等提出了基于正交迭代的多目视觉位姿估计算法[4],进而开展了火箭起飞过程的研究。但是激光雷达成像效果不直观、人眼判读性差且在火箭发射过程中易受到外界因素干扰,传统的基于视觉信息的方法则受成像质量影响,参数计算精度有待提高。
近年来,深度学习方法相关的理论研究和工程应用逐渐增多,取得了比人工判断或传统方法更优异的效果,因此被广泛应用于航天领域[5-7]。其中,杨名基于深度学习的三维点云重建方法[8],利用可见光图像完成了对空间非合作目标的三维建模,在复杂的空间环境中仍能恢复完整的点云数据。
在计算机视觉中,这种三维重建的方法指根据图像重建三维信息的过程。重建的数据格式主要包括四种:深度图、点云、网格以及体素。其中点云数据具有简单、无需排列和组合连接、在几何变换和变形时更容易操作的特点,因此更利于重建并还原模型的位姿特征,适用于不考虑重建结果纹理、外观因素的任务场景。
三维点云重建网络使用的图像包括单视图或多视图,其中利用多视图的三维重建相对更容易实现,例如Point-MVSNet通过对不同角度的图片进行点云特征提取再融合的方法,生成了最终的点云[9]。但是基于多视图的方法往往不适合处理实际仅有一台摄像机的情况,且计算复杂,实时性较差。而单视图仅使用单一摄像头作为采集设备,具有成本低,易于配置等优点,但由于信息不完全,重建难度较大,会产生不确定的结果。为了解决该问题,Fan等人生成了多个重建结构,并通过结构的对比与融合,得到了最优点云[10]。后续的大量研究则专注于提高单视图重建点云的精确性,包括将单阶段的点云预测转化为分阶段处理的DensePCR[11]模型与利用图卷积网络实现特征解码过程的PCDNet[12]等。由于真实场景下助推器图像数据采集设备单一,本文使用了一种基于单视图的三维点云重建网络,实现了助推器目标关键点云的精确生成。
三维点云重建广泛应用于医学、地质、航空航天等各项领域[13-16]。实际应用时,往往会对重建的点云进行配准、拼接、特征分析等进一步的操作。在航天领域中,利用三维点云重建进行目标的运动参数估计就是一项关键的技术应用。本文利用神经网络强大的拟合能力,寻找到了一个模型来逼近图像到点云的映射,实现了火箭助推器的点云重建及位姿估计的完整流程。总结来说,本文的贡献在于:考虑真实环境构建了助推器分离仿真数据集;提出了一种利用三维点云重建进行助推器位姿估计的新的流程,并得到了精确的估计结果。
2 位姿估计方法
2.1 模型数据集的采集与处理
本文借助Blender三维设计软件与Python编程语言完成了火箭助推器图像与点云的对应数据采集。
首先对火箭助推器进行了模型建立,参考公开的助推器模型进行了删减、修改以及尺度的调整,具体包括直径、长度等,完成建模过程后将模型导入了Blender软件。Blender具有脚本自动采集数据的功能,可以通过编写Python代码控制助推器在世界坐标系下的位置与欧拉角姿态。每次助推器位姿变化后,采集当前摄像机的拍摄画面以及模型的点云,即可获得一对图像与点云的对应数据。助推器的点云默认为整个助推器的稠密点云,为了加速训练,从中筛选出了3 373个可反映目标位姿的关键点构成了新的点云,同时保持了原有模型对称结构的特性。图1给出了助推器模型以及最终保留的点云示例。
为使数据集中的图像更符合真实条件下的相机成像结果,我们添加了背景,将助推器质心的水平、竖直、深度坐标分别控制在[-79.1 m,-2.1 m],[0.3 m,57.1 m],[26.7 m,400 m],俯仰角和偏航角分别控制在[-π/2,π/2],[-4π/3,4π/3],同时通过随机加噪的方式进行了数据增强,在数量和类型上都保持了丰富性。最终获得的数据集共包含12 800张尺寸为128×128像素的图像,即12 800对数据。图2给出了部分数据集的图像示例。
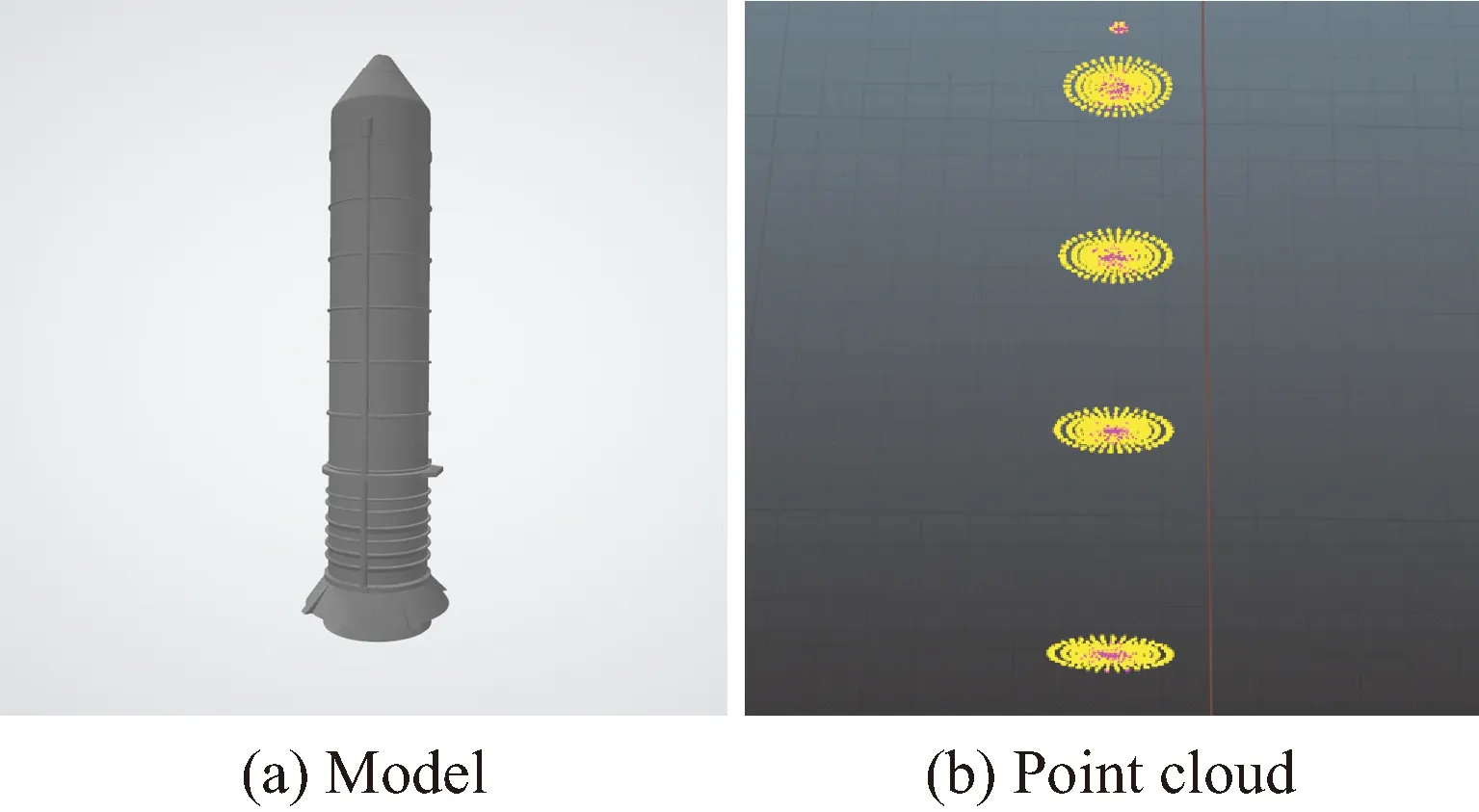
图1 火箭助推器的模型与关键点云Fig.1 Model and key point cloud of rocket booster
可以看到,数据集图像中既包括不同位置与姿态的助推器,也包括遮挡(下2,下3)、部分超出视野范围(上3,下1)等特殊场景下的图像,有利于鲁棒性的模型训练。
为了缓解输入数据不同维度差别较大产生的影响,避免随机梯度下降法趋于局部鞍点,可对图像数据进行简单的归一化处理,采用公式如下:
式中:ir,g,b表示原始图像三通道的像素值,Ir,g,b表示归一化的像素值。
2.2 三维点云重建网络的建立
本文选择的基本三维点云重建网络框架为PointOutNet[10],该模型可以端到端地完成从单视角的RGB图像到三维点云的重建。图3展示了模型的整体结构,其中编码器用于提取输入图像I∈128×128的特征,解码部分同时将特征分别送入反卷积和全连接两种结构中。建立编码器-反卷积支路时,采取了沙漏结构,即连接不同尺度的多层编码结果与反卷积结果,并重复进行编码-解码的过程。编码器-全连接支路则直接对编码特征进行了解码。对比两个支路,反卷积结构更擅长捕获目标的主体部分,而全连接则更擅长补充细节形状部分,两者在点云重建方面具有互补的效果。因此最终通过直接连接两部分的解码结果构成了输出的点云集合S∈N×3。
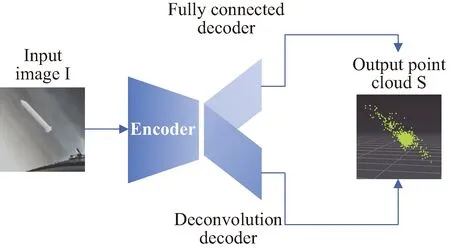
图3 三维点云重建网络结构Fig.3 3D point cloud reconstruction network structure
在构建损失函数时,模型使用倒角距离(chamfer distance,CD)进行了生成点云和真实点云的距离计算,它的计算公式如式(1)所示,是对称形式的CD,满足作为度量的定义。
(1)
式中:S1和S2表示两个不同的点集,点的数目可以不同,x和y分别表示来自这两个点集中的点。实际计算时,将真实点云和模型生成的点云数量均控制为3373,即S1,S2∈3373×3。
2.3 三维点云重建网络的训练
三维点云重建网络基于最小化式(1)进行模型的训练与参数的更新。为了防止模型过拟合,在实际训练过程中额外添加了L2正则化损失项。该项将促进对模型参数较大时的惩罚,控制模型的权重参数保持在较小的范围内。结合两部分损失函数的总体损失函数如下式:
式中:G表示建立的神经网络,I和S表示图像与对应的真实点云,w表示网络G中的权重参数,α和β为两个超参数,分别控制了点云重建损失项与正则化损失项。
2.4 基于主成分分析的位姿估计
基于2.2和2.3节获得的点云重建结果将包含目标全部点的三维坐标。为了进一步得到助推器的位姿参数,本文基于这些数据进行了主方向的计算,根据火箭助推器的形状特点,它的主方向将近似对应于头尾连线方向。
主方向的计算方法为主成分分析(principal components analysis,PCA),该算法用于对高维数据降维,它将高维数据投影到低维超平面,最大化投影后的点方差,使信息量达到最大。
具体实现时,将三维点云数据降为一维,即寻找到一个主方向u=(u1,u2,u3)T,令点云数据在该方向上的投影方差尽量大。其中,u1,u2,u3分别表示水平、竖直、深度方向上的值,根据u即可估计助推器的位姿参数,如下所示:
式中:pmin和pmax分别表示主方向上的两个投影端点对应的原始三维点,据此得到了中心点p0。即助推器的位置参数可由x0,y0,z0表示,而θ,ψ分别表示俯仰角和偏航角,由于助推器模型为对称结构,因此无需计算滚转角,θ和ψ即可代表完整的姿态参数。
3 试验结果
3.1 试验配置
试验所用数据集为2.1节介绍的图像-点云数据集,其中12 160张图像用于训练,640张图像用于测试。训练时设置batchsize为128,训练轮数epoch为5 000,优化器为Adam优化器,初始学习率为3×10-3并随训练轮数增加进行衰减,随机种子设置为1 029。为了便于判断点云重建的精度是否足够高,同时防止正则化部分损失过大,分别将超参数α和β设置成10 000和0.1。考虑全连接解码器和反卷积解码器分别擅长重建细节和整体的特点,它们输出的点云数目比例应远小于1。实际的配置中,我们将它们输出的点云个数分别设置为301和3 072,比例约为1∶10。全部试验在Linux系统下使用NVIDIA 1080 Ti GPUs完成,所用深度学习框架为tensorflow。
3.2 位姿估测结果
基于2.1、2.2和2.3节的方法,对图像中的助推器目标完成了点云的重建,测试图像与对应的重建结果如图4所示。通过观察重建点云的不同视角可以看出,训练后的模型可以关注图像中的助推器目标并重建其点云,而不会受到背景或遮挡等外界因素的干扰,主观上重建效果较准确。

图4 测试图像与点云重建结果Fig.4 Test image and reconstruction result of point cloud
为了定量评估以上点云重建网络的准确率,根据最终训练得到的模型,计算了全部测试图像对应的真实点云与生成点云的点距离均值、标准差、最大值与最小值,并将它们作为点云重建准确率的评价指标。根据2.2中点云数量相同的设置,可以对真实点云与生成点云进行一对一的匹配,具体来说分别将两组点云按三维坐标升序排列,即可按顺序一一对应。每对点的距离使用欧式距离计算,进一步可以得到每张测试图像的均值、方差等四项指标。对全部测试图像的指标取均值的结果如表1所示。

表1 重建结果的误差
根据表1可以看出,在本试验的数据范围下,重建点云与真实点云的点距离平均值、标准差、最大值、最小值分别约为8.1 m,17.39 m,3.1 m,7.8 m。说明点云重建误差较小,但相对波动较大,整体分布可能存在差异,影响后续的位姿估计。经分析,这可能与筛选后的真实点云并不连续有关,导致网络难以训练,最终生成的图像更类似于图4所示的助推器整体而非图1(b)的多个圆环。
根据2.4节的方法,我们进一步得到了助推器目标的主方向如图5所示,直观上主方向与助推器朝向(头尾连线方向)一致。根据主方向我们完成了对位置与姿态的估计,并在全部测试集上进行了真实位姿与估计位姿的对比。图6是水平位置x、竖直位置y、深度z、俯仰角θ、偏航角ψ的仿真值与估计值的曲线,其中每组曲线的横坐标无单位,表示图像排列后的序号,排列方法为按照当前位姿量的真实值升序排列。

图5 测试图像与点云主方向Fig.5 Test image and main direction of point cloud
从图6中可以看出,位置的估计值与真实值基本重合,说明估计较为准确,而姿态的估计值虽然存在抖动现象,但变化趋势与真实值基本相同。
为了进一步定量说明估计的精确程度,我们计算了回归问题中常用的平均绝对值误差(mean absolute error,MAE)与决定系数R2 score两个指标,并依据计算结果对位姿的估计进行了评估与分析,MAE和R2 score的计算方式如下:
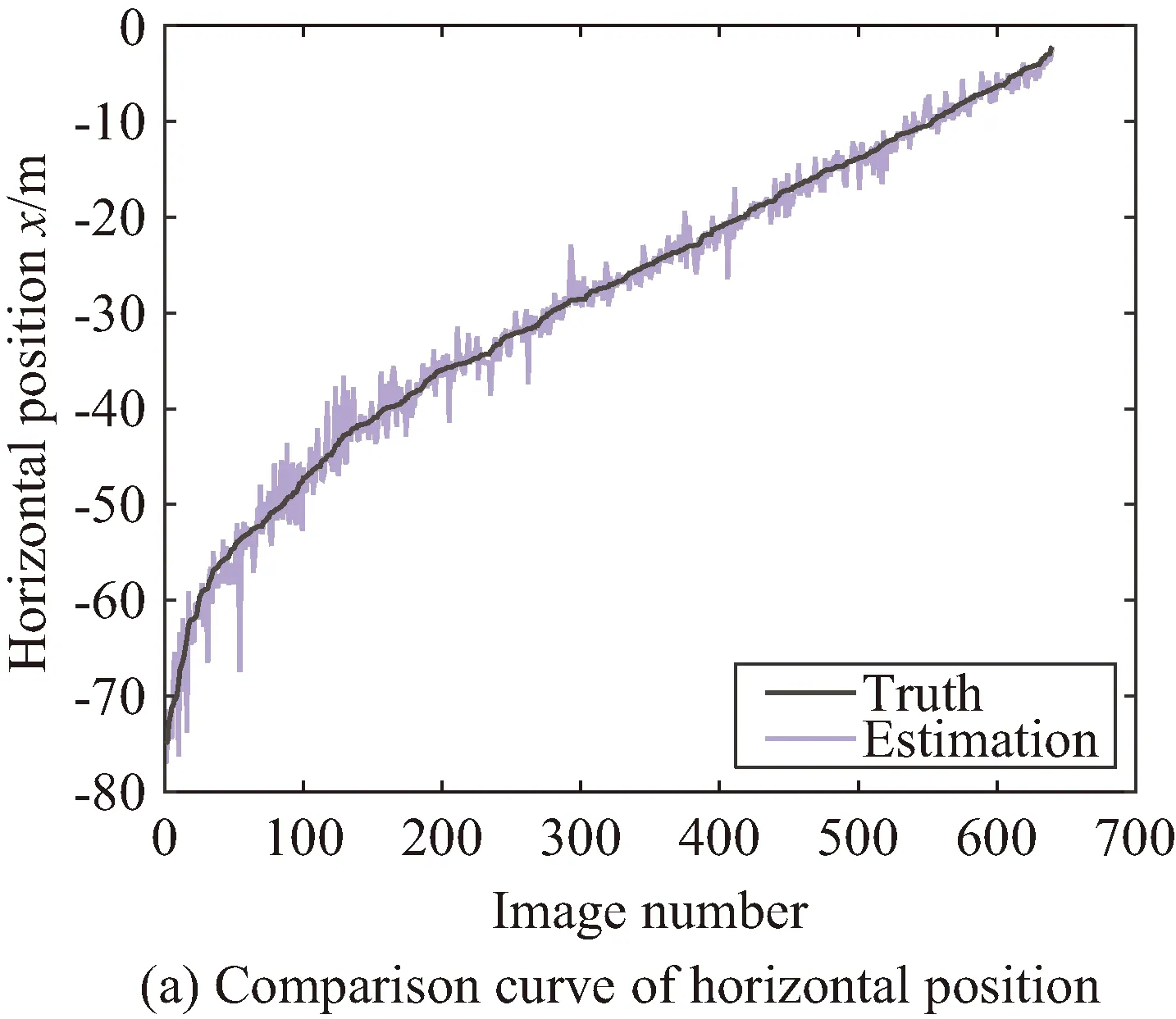
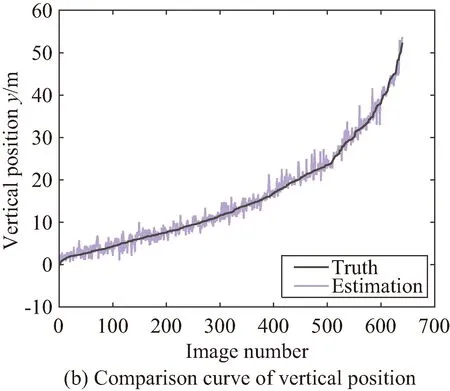
图6 位姿估计值与真实值对比Fig.6 Comparison curve of estimated pose and true pose

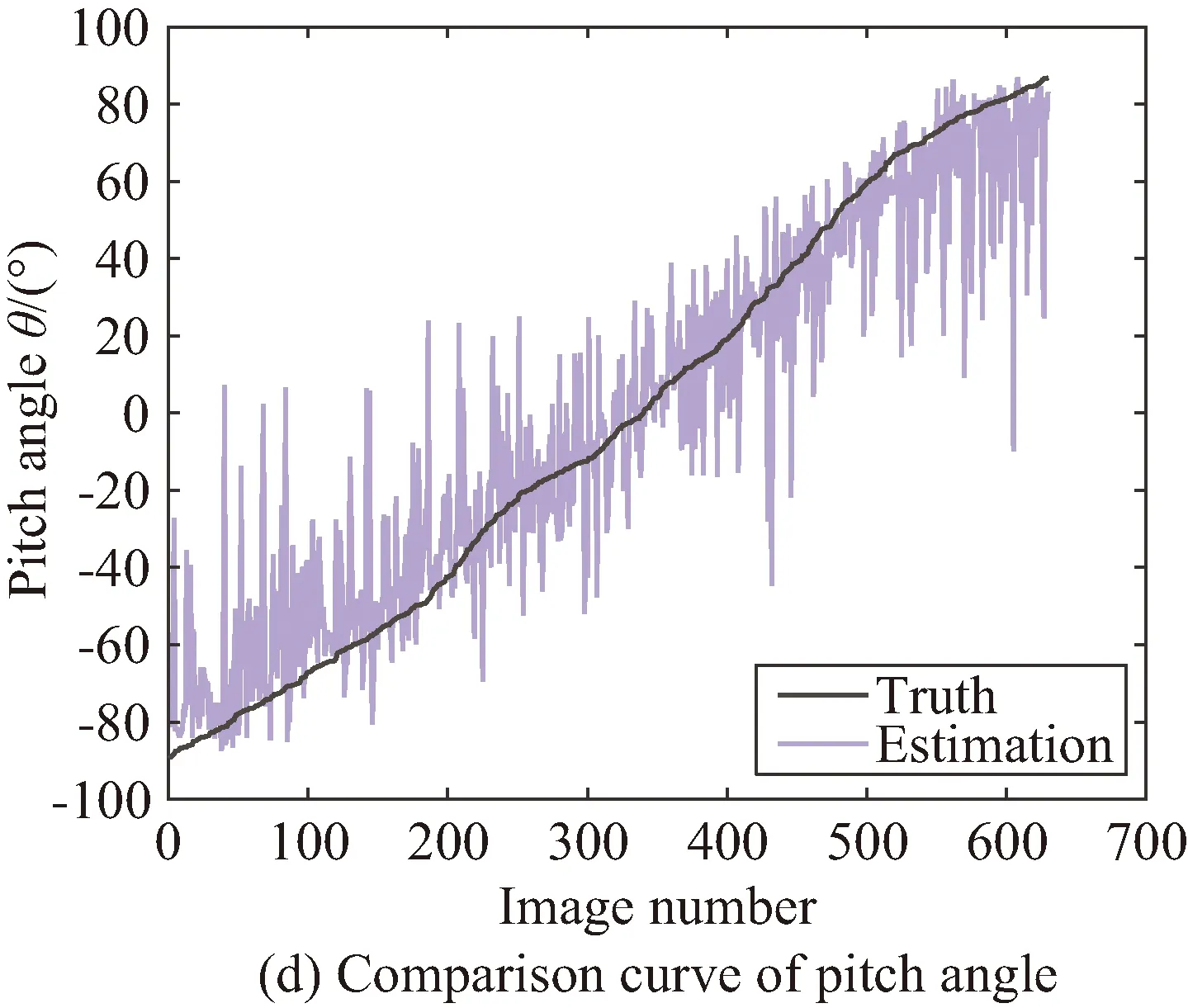
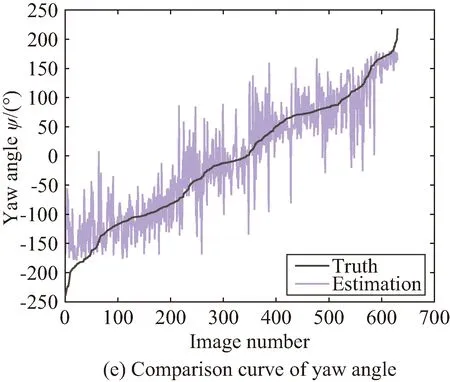
续图6Fig.6 Continued
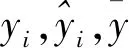
表2、3给出了多个位姿量在两项指标下的计算结果。可以看出,在MAE指标下,不同维度的三维坐标误差存在差距,最低在1.1 m左右,而最高在5.2 m左右,俯仰角误差约为12.9°,偏航角误差约为29.9°。由于试验中,俯仰角和偏航角的误差相差较大,额外添加了姿态平均误差用于计算二者的均值,综合考量了助推器姿态估计的准确程度,计算得到的姿态平均误差在21.4°左右。实际上,相对于数据范围而言,MAE指标下的估计误差反应出了较精确的结果,但该项指标的计算较简单,不便于对比不同数量级的数据,因此不同维度的误差值之间偏差较大。
与MAE不同,R2 score可理解为将均值作为了误差基准,基于预测误差和基准误差的相对值进行了指标计算。R2 score考虑了数据本身的范围,最终的误差具有相同的范围与衡量标准,便于对比。而我们在R2 score下,位置估测结果均取得了0.98以上的分数,且几乎无偏差,反应了在各自的坐标估计量下,预测值与真实值基本一致;对欧拉角估测结果的平均分数在0.81左右,且俯仰角与偏航角相差较小,表明了最终对目标姿态的估计结果也较为准确;对不同维度的R2 score进行算数平均与按方差加权平均的结果分别约为0.92和0.90,说明了整体上我们的方法具有较强的位姿估测能力,能精确预测需要估计的全部未知量。
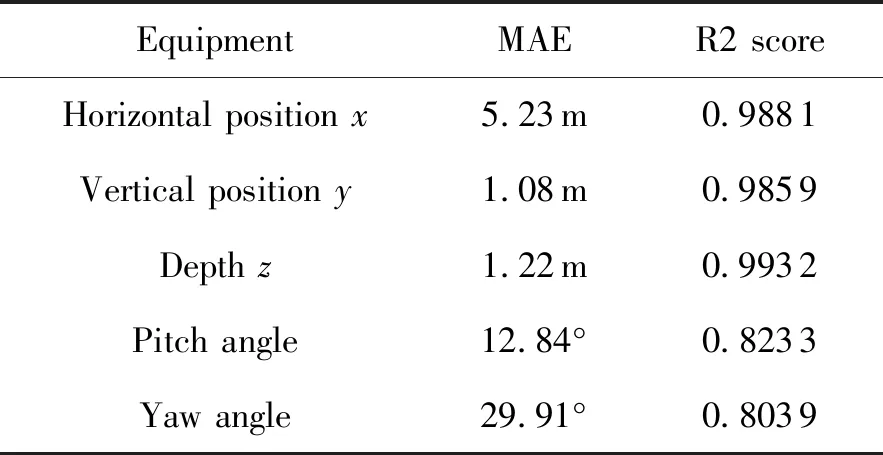
表2 估测结果的误差

表3 估测结果的平均决定系数 R2 score
4 结论
本文提出了一种基于三维点云重建的助推器位姿估计方法,与现有方法不同,本文基于深度学习的方法实现了助推器三维点云的重建,并利用主成分分析完成了位姿的估计。最终通过定量观察与定量评估,展示了本文方法在位姿估计上的精确性。具体结论如下:
1)本文方法采集了充足的图像与点云仿真数据,数据集具有多样性,能够支撑后续的网络训练与测试。
2)本文方法训练的神经网络可以生成出单张RGB图像中助推器目标的点云,即使目标部分被遮挡、不完整或存在背景干扰,也能精确重建。
3)本文方法可以通过PCA寻找与助推器实际方向一致的主方向,并进一步实现精确的位姿估计,具有良好的性能。例如在R2 score指标下,全部测试集的三维坐标预测准确率均达到0.98以上,俯仰角和偏航角的预测准确率均达到0.80以上,平均预测准确率为0.92。
在未来的工作中,为了使本文方法可对实际或仿真的助推器运动视频进行位姿估计,除了直接使用已有模型与方法对每帧图像进行处理外,仍需要进行多方面的优化,例如针对实际场景下拍摄的图像扩充数据集,考虑多帧位姿预测值的平滑,根据视频序列的相关性对模型进行修改等。
