多空间机器人协同工作空间的数值求解方法

龚轲杰，王勇，段玉瑞，梅亚飞，廖瑛

1. 国防科技大学 空天科学学院，长沙 410073 2. 宇航动力学国家重点实验室，西安 710043 3. 航天器在轨故障诊断与维修重点实验室，西安 710043

1 引言

2021年4月12日，诺斯罗普·格鲁曼公司的任务扩展飞行器(Mission Extension Vehicle-2，MEV-2)与“国际通信卫星”10-02成功实现对接，通过接管姿态和轨道控制为后者提供在轨延寿服务。除了在轨延寿，在轨服务的应用前景还包括在轨维修、更换模块、垃圾清理等[1-2]。作为在轨服务的关键技术之一，空间机械臂可承担抓捕、消旋、转运等重要操作[3-4]。随着服务对象的不断扩展，加之航天任务对可靠性的极高要求，单臂乃至多臂空间机器人将面临一些难以胜任的操作任务。而小卫星的应用和编队技术的成熟，使得多空间机器人协同服务成为可能[5]。

文献[6-8]于2010年提出了采用多自由飞行服务机器人协同操作被动目标的概念。每个机器人均配有操作臂和开关推进器，通过协调控制机械臂施加外力的方向，实现对被动目标的转运等操作。他们还详细给出了这一概念与单个大型空间机器人的区别[9]。文献[10]提出了应用组队的自动化空间机器人在轨搭建诸如太阳能站、空间遥测站等大型结构，各机器人具备不同功能，包括多臂集成机器人、转运机器人以及观测机器人等。国内有学者研究了双机器人在轨操作柔性梁的问题[11]。还有学者研究了利用编队飞行空间机器人联合定位合作[12]、非合作目标[13]的技术，以及任务规划问题[14]。

工作空间(workspace)是机器人运动学分析中的必要环节，是判别其性能优劣的一个关键的定量指标，也是开展任务规划的前提条件[15]。由于空间机器人的基座与机械臂之间存在动力学耦合，地面机器人的工作空间研究方法难以直接应用，需要开展新的探索。文献[16]对三自由度肘式空间机械臂的工作范围进行了讨论。文献[17]提出了一种巧妙的建模方法，利用质心方程，将真实模型转化为一系列链接在虚拟地面(virtual ground, VG)的虚拟连杆矢量，称为虚拟机械臂法(virtual manipulator approach, VM)，并在此基础上进行了平面单臂两关节机器人的工作空间分析。文献[18]基于该方法建模，采用蒙特卡洛法求解了单臂多自由度空间机器人的工作空间。文献[19]首先推导了3种模式下的运动学方程，然后分别提出工作空间求解策略，并以三旋转关节空间机器人为例进行了计算。

固定基座双臂机器人或者两个单臂机器人的协同工作空间往往被定义为两个末端各自工作空间的交集[20]。其实际含义是，目标处于该范围内的任意一点，两末端均可到达，并能执行相应任务。采用解析法计算工作空间难度较大，所以通常采用数值方法进行求解分析。一类数值方法是对得到的两个工作空间点集进行处理：首先建立包络所有点的长方体，再参考精度需求，将该立方体划分为微小子网格，然后仅保留同时包含两个抓捕臂末端位置点的子网格，最后利用保留下来的子网格内的点绘制得到协同工作空间[21]。另一类是从点集中提取工作空间的边界点，并借此拟合出封闭的边界曲线，然后通过射线方法求得交集的边界曲线，从而绘制出协同工作空间[22-23]。

而对于双臂空间机器人，由于基座与各臂之间均存在动力学耦合，某一臂的运动不仅会带动基座运动，也会影响另一臂末端位姿，因此其工作空间分析问题难度更大，目前这一方面的研究仍较少。文献[24]针对一种双臂空间机器人的二维地面实验系统，采用蒙特卡洛法，分别求解了单臂工作空间和双臂协作工作空间，但该文中建立的运动学模型是以基座固连坐标系为参考，并未考虑两臂及基座之间的耦合问题。文献[25]基于改进的VM法搭建了双臂空间机器人模型，采用蒙特卡洛方法分别求解了基座姿态无约束下的单臂独立工作空间、单臂牵连工作空间以及双臂紧协调工作空间，发现均呈圆环状，并得出了相应的几何参数。

多个空间机器人的协同工作空间可以继承传统定义，但应当有所扩展。一是机械臂与基座的动力学耦合，引起基座位置的不断变化，分析协同工作空间时参考坐标系的选取必须有所创新；二是因为两空间机器人各自的抓捕臂有对应的抓捕点，只要各自的抓捕点处于相应的工作空间内，服务系统即可完成抓捕任务。目前针对多个空间机器人协同工作空间问题的研究还很少。另外，传统的协同工作空间概念缩小了多机器人可协同执行任务的工作区域，对某些任务增加了不必要的约束。

本文针对空间机器人协同抓捕目标并在轨更换模块这一背景，设计了多空间机器人服务系统。相比于传统的单臂乃至多臂空间机器人系统，通过编队协同方式构建的多空间机器人服务系统具有诸多优势和发展潜力：

1)多个体协同，有效载荷相对分散，任务分工明确，一定程度上可以避免单空间机器人因卫星或机械臂故障失效等导致整个任务失败。

2)在轨操作本身由一系列精细复杂的动作连贯而成，目标的抓捕与固定是其中十分关键的环节之一。协同固定方式可有效提升系统的稳定性和任务执行的可靠性。

3)对于大体积、大惯量目标，单空间机器人操作会出现工作空间覆盖不够，捕获后组合体难以稳定等问题。而通过协同操作可以灵活选取停靠位置，保证对可抓捕点和操作点的完全覆盖，对目标快速消旋稳定等，大大提高了任务的灵活性和可靠性。

4)在轨操作任务成本很高，而小质量卫星具有发射成本低、机动能力强、节省燃料等特点，利用这些优势，发展以小质量卫星为载体的空间服务机器人，再进行灵活组合，可大大提高任务的多样性和重复利用能力。

针对上述系统，本文基于旋量理论建立了系统运动学模型，分析了传统交集式协同工作空间。进一步提出一种新的广义协同工作空间概念，并给出了数值求解方法。最后通过仿真进行验证分析。广义协同工作空间为任务规划提供了更宽泛且可执行的选择，而且在一定程度上可以降低碰撞的风险，提高协同任务的安全性。

2 系统设计与建模

2.1 系统设计

本文设计了如图1所示的多空间机器人服务系统，包含双臂空间机器人、单臂空间机器人和观测空间机器人。系统内各空间机器人以编队形式运行，相互独立，无主从关系，但可以共享信息数据，并根据任务需求相互协同。

图1 多空间机器人服务系统Fig.1 Multi-space-robot serving system

双臂空间机器人(简称为双臂系统)由基座、抓捕执行臂和操作执行臂构成。抓捕执行臂负责到达指定抓捕位置，利用对接、机械锁死等方式与目标卫星形成刚性连接，并在操作任务过程中提供稳定保障。操作执行臂则通过携带的任务专用末端执行器完成在轨更换模块操作。

单臂空间机器人(简称为单臂系统)结构相对简单，仅有基座和抓捕执行臂。其主要任务同样是与目标卫星形成刚性连接，与双臂系统的抓捕臂协同完成捕获以及消旋，并在更换模块过程中提供可靠的稳定性。

观测空间机器人携带了高精度观测载荷，具备更好的信息获取能力。一方面，在靠近目标过程中，观测空间机器人需要测量目标姿态角及相对距离等数据，同时还要估算目标的惯性参数、自旋速度等信息；另一方面，在抓捕过程中，观测空间机器人会实时获取机械臂末端和目标的状态，保证抓捕以及操作任务可靠完成。由于其不参与抓捕过程，所以建模时不作讨论。

2.2 系统运动学建模

文献[26]中采用旋量方法详细推导了多臂空间机器人的正逆运动学模型，这里不再赘述，直接基于所得结论建立服务系统的运动学模型，为后文进行协同工作空间分析提供理论基础。

图2给出了服务系统的简化模型示意，图中各符号的定义如下。为了区别单臂和双臂系统，在各量右侧分别添加下标(·)s,(·)d。

1)ΣG表示全局惯性参考坐标系。不失一般性，可以令该坐标系原点处于服务系统与目标组合整体的质心处。

2)ΣDI,ΣSI,ΣT分别表示双臂系统、单臂系统和目标卫星的固连惯性坐标系，其原点均位于各自系统的质心处。

3)向量Gpd表示双臂系统质心在全局惯性系中的位置矢量。

4)向量Gps表示单臂系统质心在全局惯性系中的位置矢量。

5)向量GpT表示目标质心在全局惯性系中的位置矢量。

6)向量Ip0d，Ip0s分别表示双臂系统、单臂系统基座在各自固连贯性系中的位置向量。

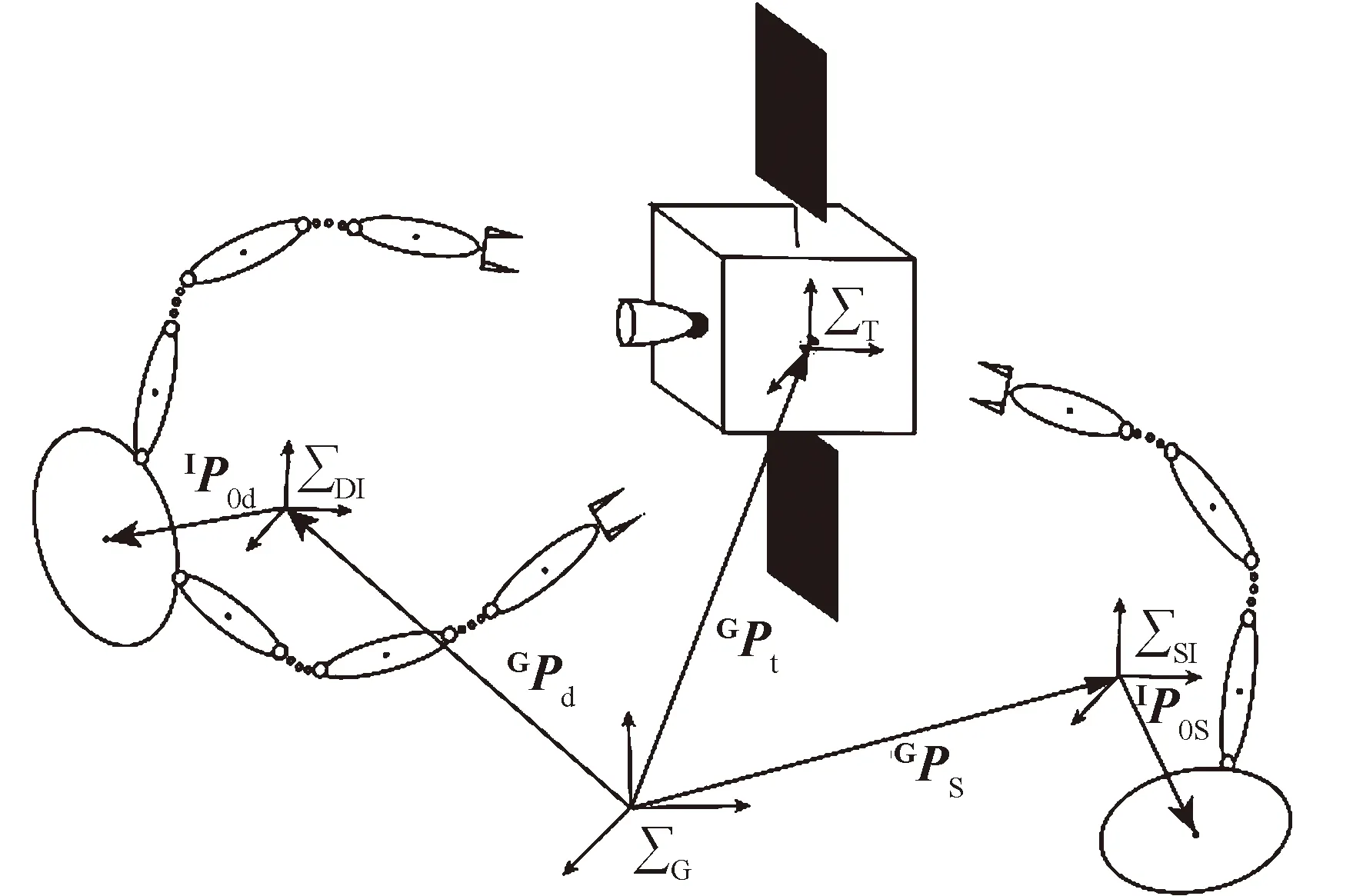
图2 服务系统的简化模型Fig.2 Simplified model of serving system

首先，分别给出ΣDI,ΣSI在全局惯性系ΣG中的位形：

由文献[26]中的运动学方程可以分别求出双臂系统和单臂系统末端在各自系统质心坐标系中的位形：

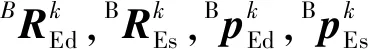
由此可分别推导出双臂系统和单臂系统末端执行器在全局惯性系中的位形：

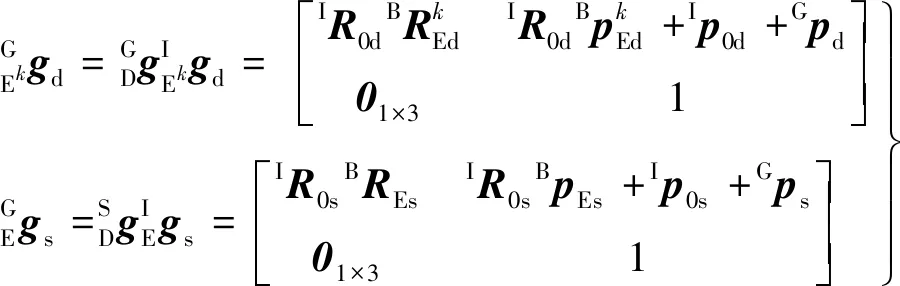
(1)

3 协同工作空间求解策略

3.1 一般协同工作空间求解

θimin<θi<θimix(i=1,2,…，n1)}

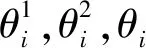
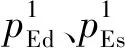
由于计算单个空间机器人工作空间采用的是蒙特卡洛数值方法，得到的是抓捕臂末端位置的点集，无法用解析法求取定义中的交集。本文采用改进的数值方法求解服务系统的协同工作空间，具体流程如下：

Step 1：设定系统的构型参数、单臂系统和双臂系统基座质心在全局惯性系下的位置，同时给出各关节角的约束。

Step 3： 基于文献[24]中的运动学方程，计算得到单臂系统抓捕臂在固连惯性系中的工作空间点集，然后根据式(1)将所有点坐标转换到全局惯性系中，从而得到集合{GpEs}。

Step 4：求出单臂系统工作空间点集的边界坐标值

然后令

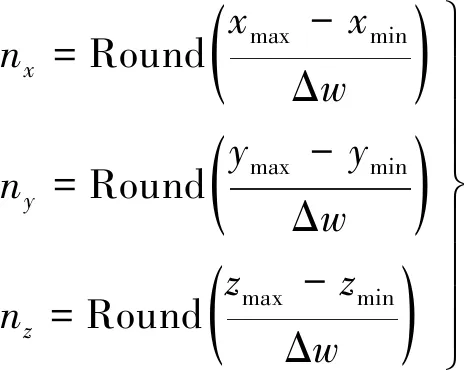
(2)

式中：Round()表示向上取整函数

Step 5：进一步令

Step 6：遍历所有子网格，剔除不包含任何点以及仅包含单臂系统末端位置点的子网格。

Step 7：利用剩余子网格内的所有点绘制出服务系统的协同工作空间。

3.2 广义协同工作空间求解

工作空间是机器人末端可达位置的集合，同时也可以理解为，当目标处在工作空间范围内，机器人才可能完成任务。而服务系统内两空间机器人协同抓捕目标时也必然存在一个可行区域，目标处在该区域时，服务系统才能完成抓捕任务。所以可将其定义为服务系统的广义协同工作空间，详细数学描述为：

式中：Ggt为目标质心在全局惯性系下的位形；Tgpd,Tgps分别为双臂系统和单臂系统对应抓捕点在目标质心固连系中的位形。

广义协同工作空间可以作为服务系统的重要性能指标之一，有必要针对此类情况进行详细分析。在实施抓捕任务时，假设目标保持不动，由空间机器人主动停靠在合适的相对位置。但以相对的思路分析，可以看作服务系统已经确定位置，通过选择合适的目标位置来确保抓捕操作可完成。根据这一思路，计算广义协同工作空间的步骤如下：

Step 1：设定系统的构型参数、单臂系统和双臂系统基座质心在全局惯性系下的位置、目标在全局惯性系下的姿态以及抓捕点在目标固连惯性系下的位形，同时给出各关节角的约束。

Step 3： 根据单臂系统的约束条件，生成一组随机关节角θsrad和基座姿态角Ψsrad。

Step 4：求出当前状态下的单臂系统末端在其固连惯性系下的位形，然后根据式(1)求出全局惯性系下的位形GpEs。

Step 5：计算出目标质心在全局惯性系中的位置Gpt。

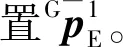
则认为该质心位置满足要求，保存至点集{Gpt}。其中ε为小量，根据精度要求设定。

Step 8：重复步骤2～7，直到得到足够的目标质心位置。

4 仿真校验

本次仿真的服务系统由一个平面双臂空间机器人和一个平面单臂三连杆空间机器人组成，双臂系统的抓捕臂和操作臂均为三自由度，惯性参数与文献[26]一致。单臂系统的构型参数与双臂系统的对应部分相同。仿真参数单位均为国际标准单位，下文不再详细给出。图3给出了初始时刻服务系统的简化示意。

两空间机器人的质心固连惯性系在全局惯性系下的位形分别为

图3 初始时刻服务系统模型示意Fig.3 Initial state demonstration of the serving system

4.1 一般协同工作空间求解

首先假设两基座姿态均无约束，并令Δw=0.1。通过Matlab编程计算得到了协同工作空间的点云图，如图4所示。将双臂系统抓捕臂独立工作空间点集和单臂系统抓捕臂工作空间点集绘制在一起，得到图5。对比可知，本文提出的算法很好地提取了交集区域的点，得到了比较理想的协同工作空间点集。

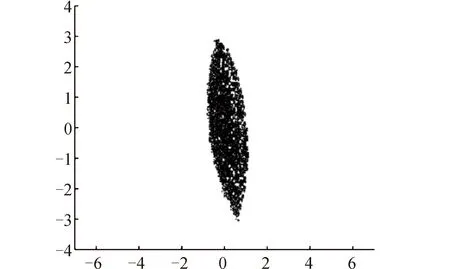
图4 基座姿态无约束时的协同工作空间Fig.4 Collaborative workspace with unconstrained base attitude

图5 基座姿态无约束时各臂的工作空间Fig.5 Workspace of each robot with unconstrained base attitude

进一步，将双臂系统和单臂系统的基座约束均设置为(-60°,60°)，计算得到如图6和图7所示的协同工作空间云图和对比。和基座姿态无约束时相比，协同工作空间范围有所缩小。从图7中可以直观地看出各臂的工作空间均缩小，且包络形状发生变化，从而导致协同工作空间缩小。

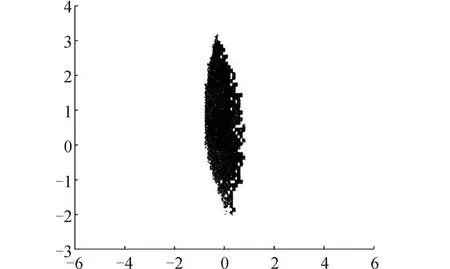
图6 基座姿态有约束时的协同工作空间Fig.6 Collaborative workspace with constrained base attitude

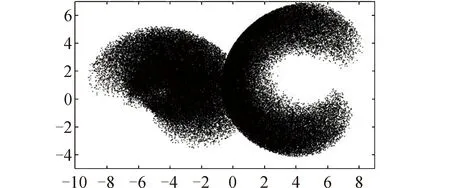
图7 基座姿态有约束时各臂的工作空间Fig.7 Workspace of each robot with constrained base attitude

4.2 广义协同工作空间求解

同样采用图3所示的服务系统为仿真对象，设定目标质心系在全局惯性系中的姿态角为Ψt=[0,0,0]T。双臂系统对应抓捕点在目标质心系中的位置为[-1,0,0]T，单臂系统对应抓捕点在目标质心系中的位置为[1,0.79,0]T。

首先计算基座姿态无约束下的广义协同工作空间，所得结果如图8所示。与图9对比可以看出，广义协同工作空间与一般概念的协同工作空间明显不同，范围较后者要大许多。这意味着目标卫星质心并不一定要处于两抓捕臂工作空间的交集内部。某些情况下，目标质心处于交集外同样可以完成抓捕任务。进一步计算了相同基座约束条件下的广义协同工作空间。与无约束时相比，范围同样有所缩小。

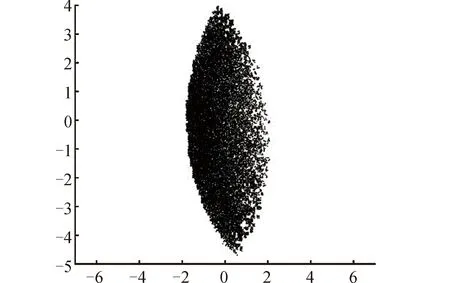
图8 基座姿态无约束时的广义协同工作空间Fig.8 Generalized collaborative workspace with unconstrained base attitude

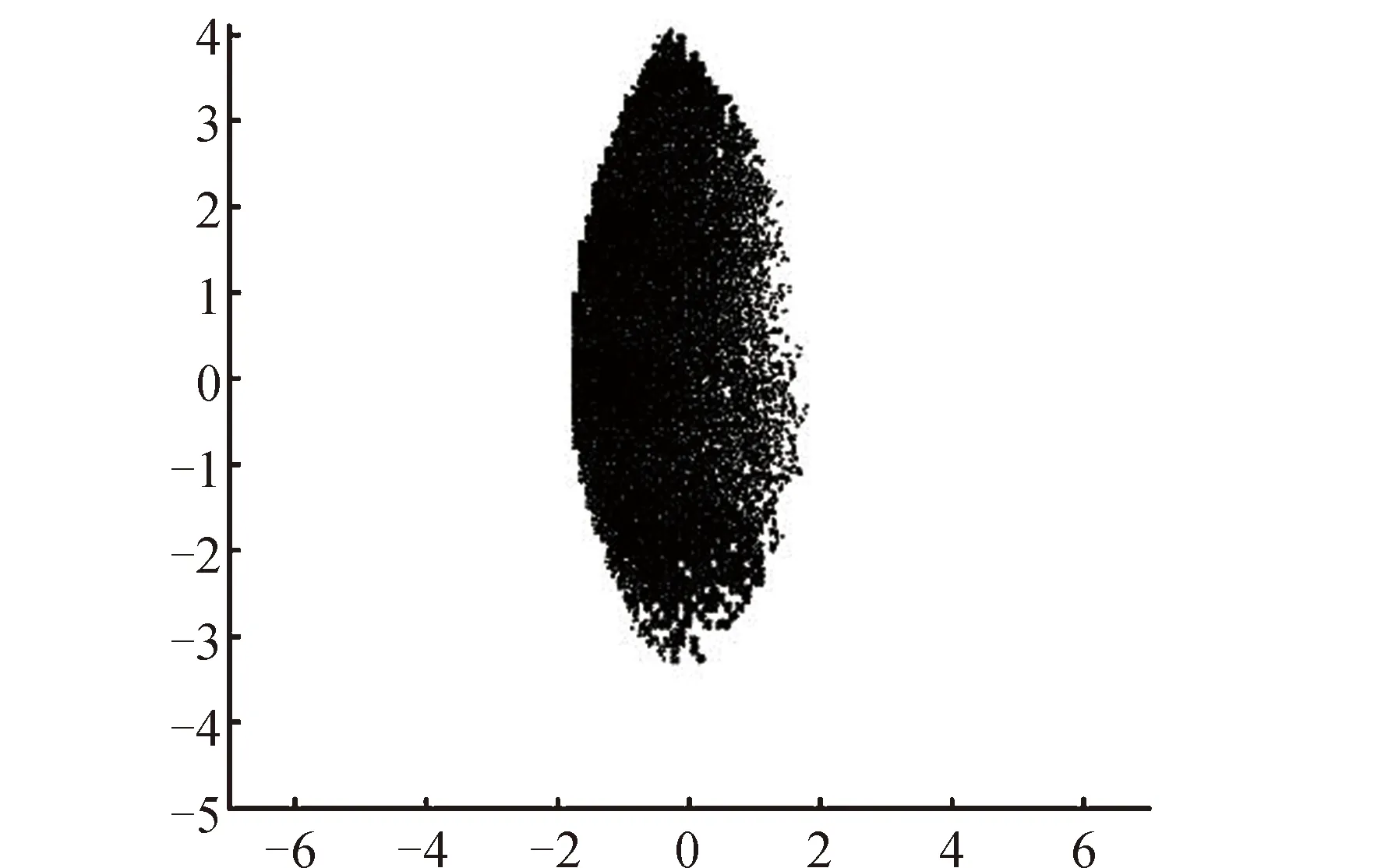
图9 基座姿态有约束时的广义协同工作空间Fig.9 Generalized collaborative workspace with constrained base attitude

考虑到某些任务会对协同抓捕构型提出要求，即对某些关节角提出特别的约束，有必要分析构型约束对协同工作空间的影响。假设基座姿态均无约束，但两个抓捕臂末关节角存在如下约束：

计算得到独立工作空间云图和广义协同工作空间，分别如图10、图11所示。从图10可以看出，由于存在构型约束，两空间机器人的独立工作空间没有交集，若按照一般协同工作空间的概念，此时服务系统将无法完成任务。但图11表明，此时系统存在广义协同工作空间，只是范围明显缩小。

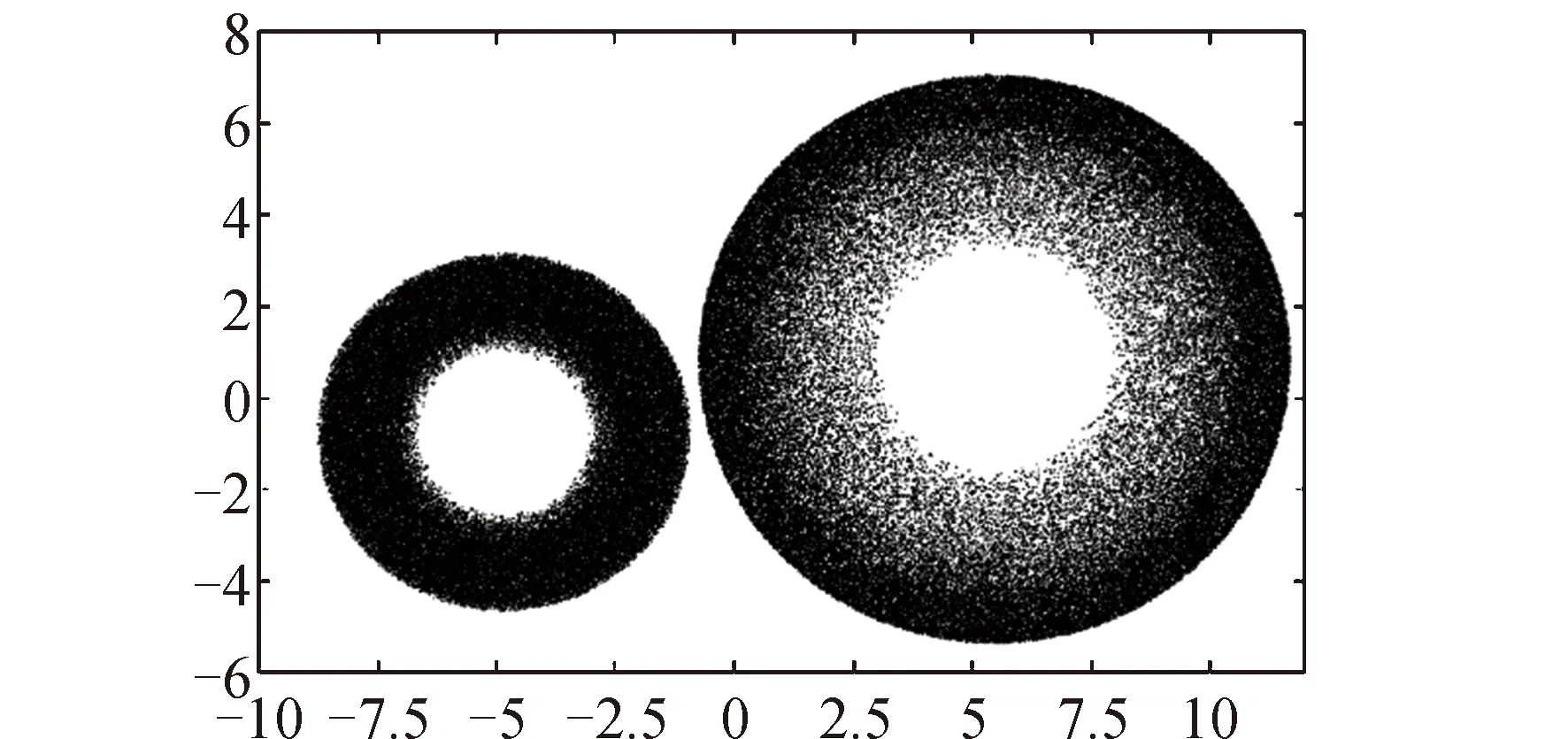
图10 构型有约束时各臂的工作空间Fig.10 Workspace of each robot with constrained joint angles

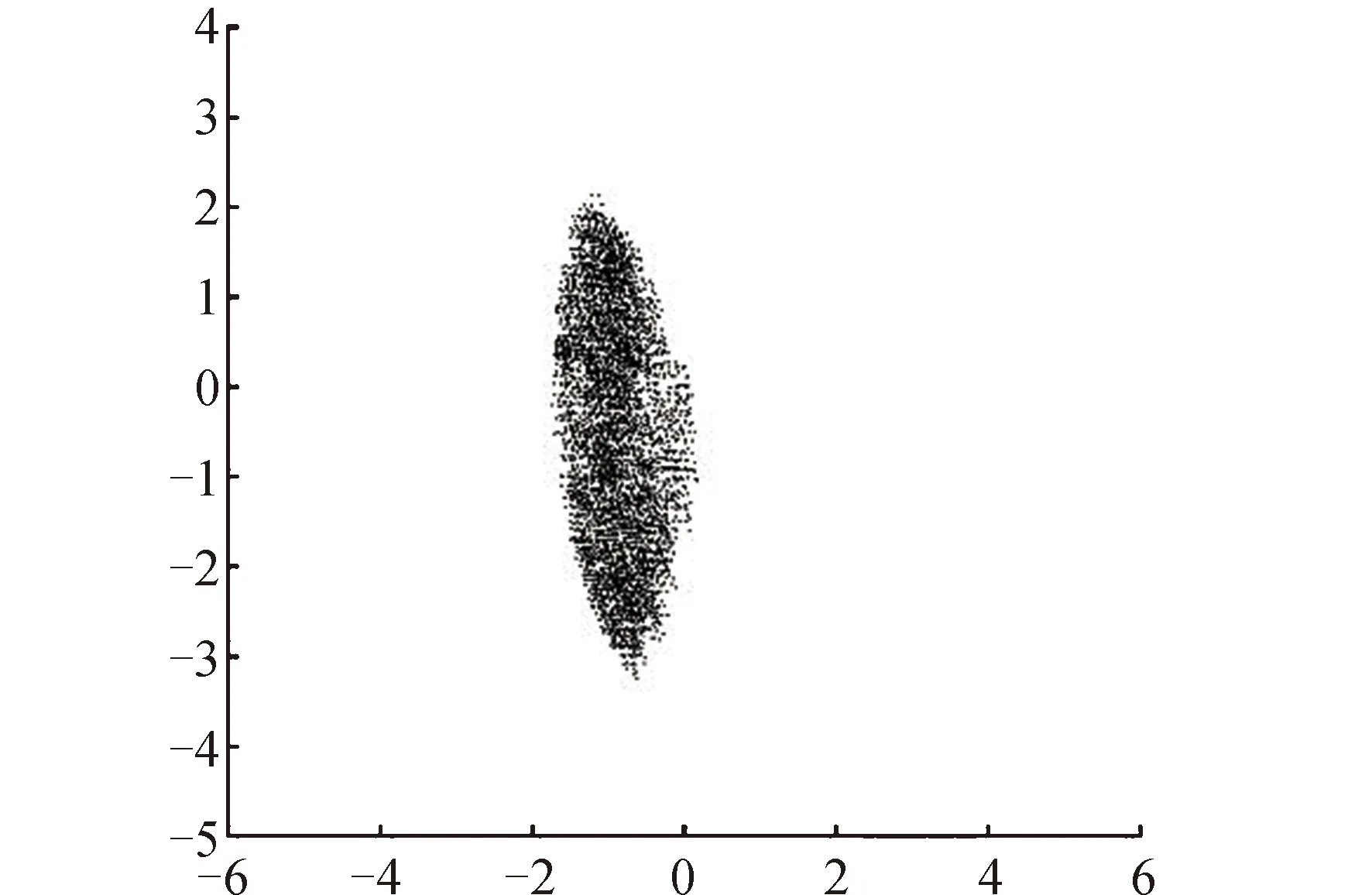
图11 构型有约束时的广义协同工作空间Fig.11 Generalized collaborative workspace with constrained joint angles

5 结论

相比于单个大型空间机器人，多个小型空间机器人协同操作具有成本低、可靠性高、灵活性强等诸多优势。考虑到空间机器人协同工作的特殊性，本文提出了广义协同工作空间的概念，并分别给出了一般协同工作空间和广义协同工作空间的数值求解方法。仿真结果表明，广义协同工作空间范围有所增大，意味着目标质心可以处在交集之外。同时，一般和广义协同工作空间均会随着基座姿态约束的增加而缩小。本文的结论可以为多空间机器人协同任务设计和规划提供定量的依据。