多约束多星快响巡察任务规划方法

彭晨远，张进,*，严冰，周洪喜，罗亚中

1. 国防科技大学 空天科学学院，长沙 410073 2. 空天任务智能规划与仿真湖南省重点实验室，长沙 410073

1 引言

在轨服务技术因具有延长卫星寿命和节约任务成本的优点，受到各个国家和机构的重视。其应用包括在轨加注、在轨巡察和在轨维修等[1-2]，具有很强的经济和军事价值。在轨巡察是在轨服务的基础，多星快响巡察是指当多个目标卫星出现不明问题时，平台在短时间内进行轨道转移，在距离目标较近时释放子航天器，对目标进行飞越巡察，平台则继续滑移，巡察下一个目标或退出任务。该类问题属于多星交会或飞越问题，同样属于快响任务轨道设计问题。

对于多星交会问题，一般分为一对多、多对多和P2P三种不同的模式，分别为一个或多个服务卫星和多个目标卫星交会以及每个卫星之间都可进行交会的模式。首先是一对多模式，Hudson等和Zhang等研究了在轨服务问题，以速度增量最优或任务收益最大化为任务指标，采用优化算法得到最优序列[2-3]，Zhang等还考虑了光照等约束。Barea等研究大规模空间碎片清除问题，以任务收益最大化为目标，得到同时满足时间和能量约束的交会序列和实际轨迹[4]。第二是多对多模式，Li等研究以燃料站和加注航天器为背景的在轨加注问题，优化任务分配和加注序列，得到了满足时间和运载能力约束的在轨加注方案[5]，Zhang等和Zhu等考虑加注站的选址和开放加注站的代价等问题，采用蚁群算法或者聚类算法确定了燃料站的位置和数量，满足在轨加注任务约束[6-8]。第三是P2P模式，Yu等考虑通信时间窗和光照等复杂约束，提出两阶段规划策略应用于P2P模式中[9]。都柄晓等以分布式在轨加注为研究对象，将该类问题转化为图匹配问题，并使用图论算法和遗传算法进行求解[10]。

对于多星飞越巡察问题，飞越巡察一般采用共面机动、异面飞越的方式对目标航天器进行近距离观测。Zhang等给出了单个航天器无需轨道机动，异面飞越三个Walker星座卫星的充分必要条件[11]。Zhou等研究了基于共面机动的多星飞越近距离观测任务，提出使用近地点机动的方式对不同目标进行飞越，并用两层优化模型优化了飞越顺序、任务时间和机动策略[12]。Zhu等在Zhou等的基础上，提出了两次共切机动的策略，使得机动位置不仅仅局限在近地点上，完成异面飞越巡察任务[13]。赵照研究了基于共面机动策略和混合编码遗传算法的多星飞越巡察任务，但是没有考虑光照等复杂约束条件[14]。麻娜提出利用向后调相机动的策略，任务星和不同轨道面上的卫星进行飞越交会，完成单个任务星对Walker星座的遍历访问任务[15]。

对于快响观测任务轨道设计，主要集中在对地观测轨道设计问题上[16-18]，思路一般为在短时间内完成对地观测等任务，尽可能减少任务星数量并提高任务收益。

在多星交会或飞越问题上，现有研究考虑的约束不能满足实际巡察任务，且对于一般的约束求解也不能保证计算的稳定和高效性。第二，对于快响任务轨道设计，现有研究集中于对地快响观测，很少有研究涉及空间任务，需进一步拓展。基于以上两点，本文研究了考虑多约束的多星快响巡察任务，并结合问题特性提出一种推进剂消耗最省或任务时间最短的贪婪搜索和多轮规划方法。

2 巡察服务平台机动策略

2.1 基于共面机动的候选巡察时刻

基于共面机动的策略，每个平台只进行面内机动，目标卫星经过平台轨道面和目标的交点时刻，记为候选巡察时刻，交点记为候选巡察位置，如图1所示，每一圈有两个候选巡察位置。通过比较两个候选位置的地影条件，筛选出其中一个作为最终候选位置：如果只有一个候选位置在地影外，则选择该位置；如果两个位置都在地影外，则选择离地影较远的一个。

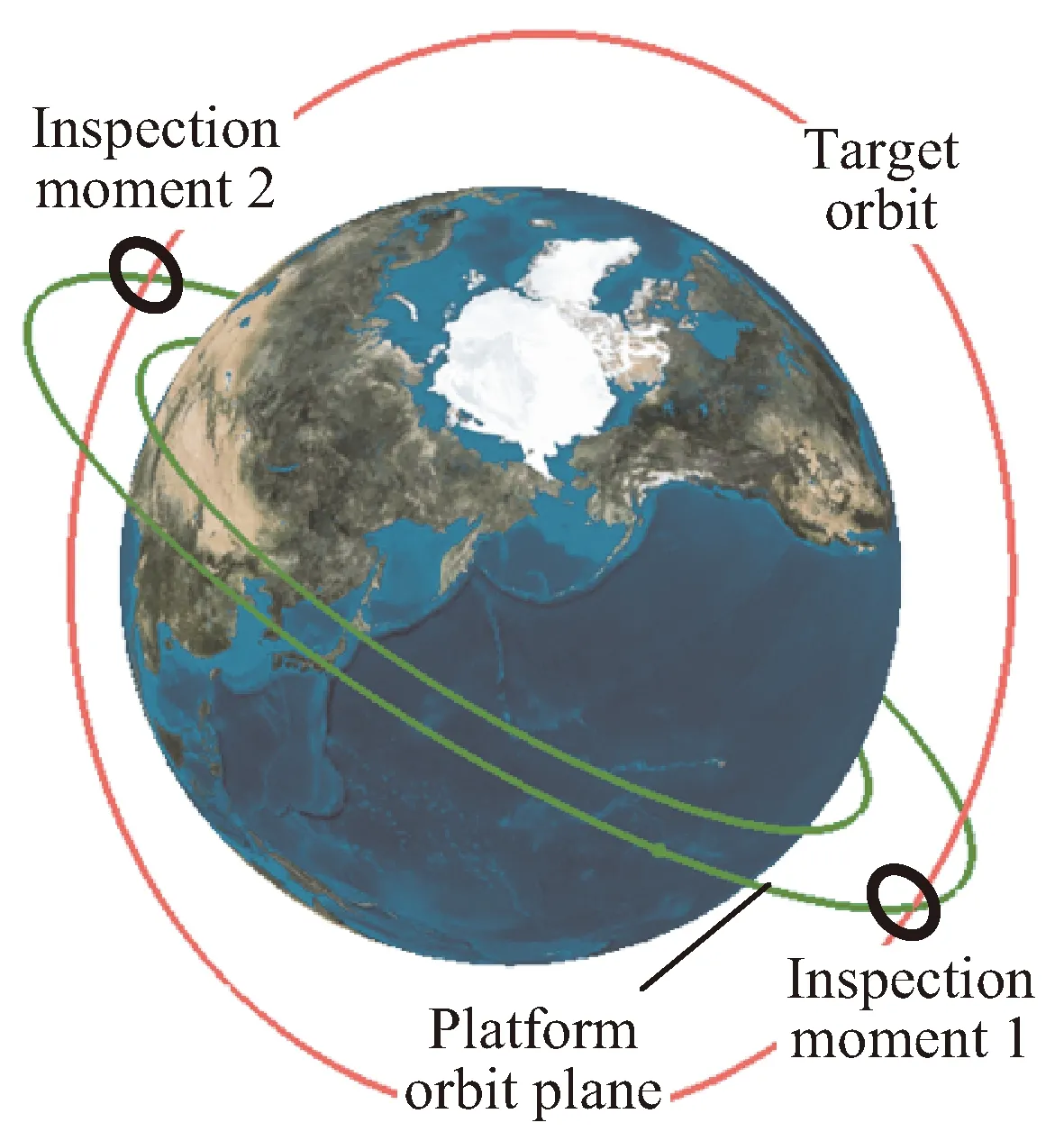
图1 共面机动策略下的候选巡察时刻Fig.1 Candidate inspection moments under coplanar maneuver strategy

候选巡察位置和时刻与平台和目标需要瞄准的纬度幅角有关，具体计算公式参照文献[14]，如式(1)和(2)所示。

(1)

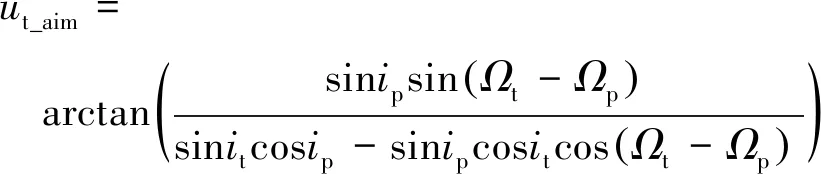
(2)

式中：up_aim为平台需要瞄准的纬度幅角；ut_aim为目标需要瞄准的纬度幅角；Ωp和Ωt分别为两者的升交点赤经；ip和it分别为两者的轨道倾角。另外一个位置需要瞄准的纬度幅角为(up_aim+π)和(ut_aim+π)。

2.2 携带子航天器的平台调相机动过程

平台的机动始终保持在初始轨道面内，当目标经过交点时，平台携带的子航天器对目标进行巡察，如图2和图3所示，一共分为4个阶段：1)初始阶段，平台经过一段任务准备时间，沿轨迹方向施加一个近地点(或远地点)机动，进入霍曼转移轨道。2)第一次经过远地点(或近地点)时，施加一个轨道圆化机动。3)平台继续滑移，在目标距离候选位置还有不到一圈时，释放子航天器，施加一次Lambert机动，在巡察时刻完成巡察任务。4)平台继续滑移，等待下一次巡察任务或退出。

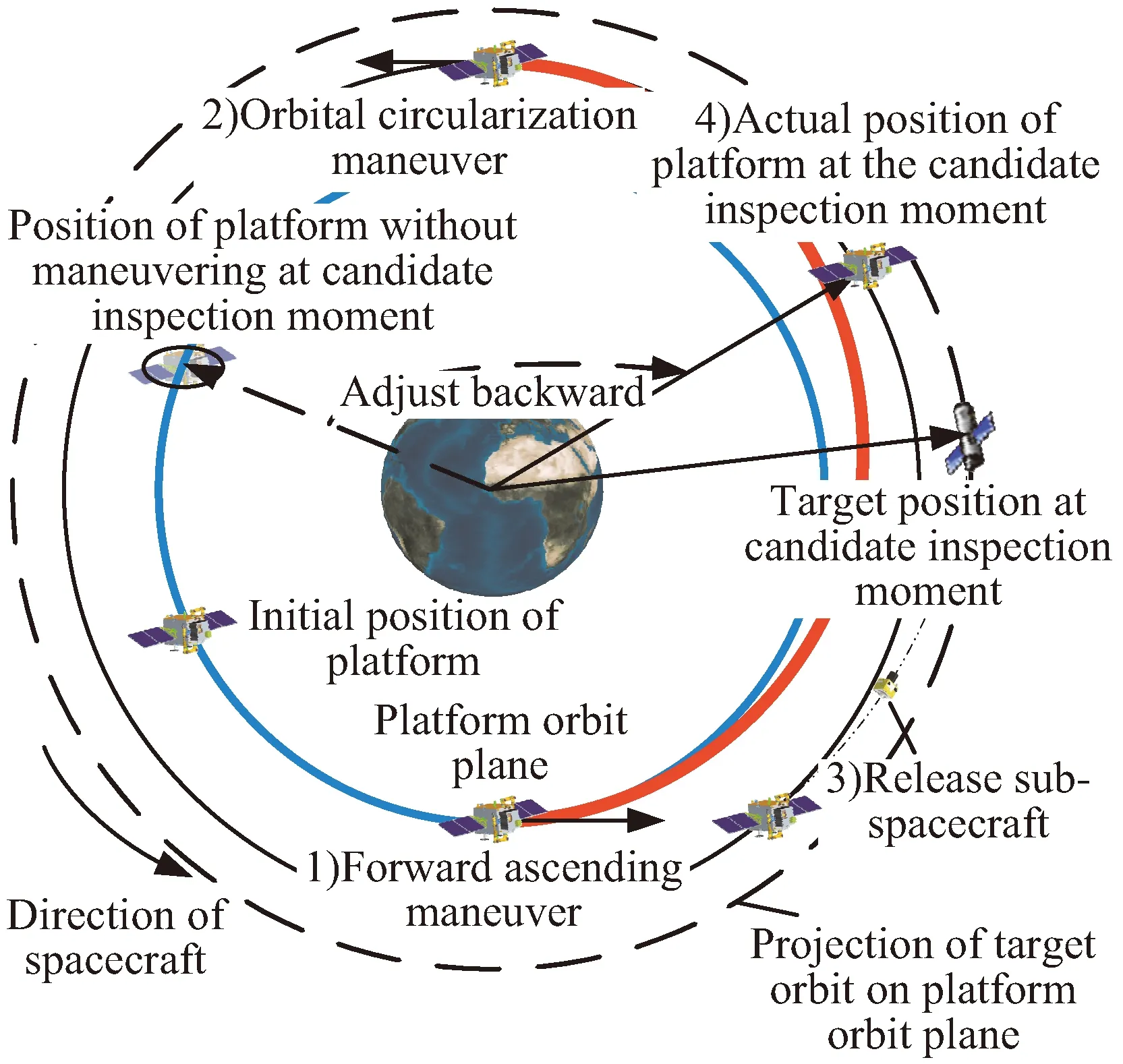
图2 平台升轨等待示意Fig.2 Schematic diagram of platform ascending waiting orbit

图3 平台降轨追赶示意Fig.3 Schematic diagram of platform descending chasing orbit

该类机动方式可以尽快进入需要的调相轨道，在任务时间较短时，单圈就可以完成调相任务；当任务时间较长时，需要多圈调相，该方法仍然成立。对于霍曼转移的调相方式，近地点高度较易计算，方便满足LEO航天器最低轨道高度的限制，大大减少了不满足实际情况解的搜索，提高了求解效率。

第一次沿迹向机动的方向分两种情况，如果向前机动，则称为升轨等待，如果向后机动，则称为降轨追赶。平台采取升轨还是降轨的策略，取决于平台无机动时，候选时刻实际的纬度幅角up和需要瞄准的纬度幅角up_aim两者的差Δu，具体计算如式(3)所示。

(3)

如果Δu=0，则不需要调整；如果Δu>0，则证明平台的相位领先于目标，那么就需要向后调整，采取升轨的策略，如图2所示；如果Δu<0，则与Δu>0的情况相反，采取降轨的策略，如图3所示。

3 多星巡察任务规划问题和方法

3.1 任务规划问题的数学模型

考虑多个平台对多目标进行巡察，平台在完成一个目标的巡察任务后，可继续执行下一个目标巡察或退出任务。对于该类多星巡察任务规划问题的数学模型，需要明确规划问题的优化变量、优化目标和约束条件，下面分别展开说明。

(1)优化变量

多星飞越巡察任务规划问题的设计变量包括两个层次的设计变量，上层为任务分配和巡察次序变量，决定了任务的主要流程；下层设计变量包括单次巡察任务所需要的时间、轨道机动的时刻和分量、子航天器释放时刻和机动分量等设计变量，决定了单次巡察任务的具体实施方案。

(2)优化目标

对于多星飞越巡察问题，优化目标一般包括两类，第一类是整个任务过程中所有巡察航天器总推进剂消耗最省，第二类是总任务时间最短。

单次巡察任务推进剂消耗的计算公式为：

(4)

式中：Mp为机动前平台初始质量；Ispc为平台发动机比冲；Δvp为平台机动的速度增量。

第一类指标是总推进剂消耗最省，即

(5)

式中：Δmij为平台i巡察目标j的推进剂消耗。 单次巡察任务结束时间为子航天器完成对目标巡察任务的时刻，对于多星巡察问题，总任务时间为所有巡察时刻的最大值，即

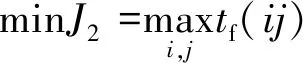
(6)

式中：tf(ij)为平台i巡察目标j的结束时刻。

(3)约束条件

约束条件分为两类，包括末端巡察约束和轨道机动约束。末端巡察约束具体如下。

1)子航天器末端一段时间内的最小阳光视线角α大于下限αmin，α的计算公式如式(7)所示。

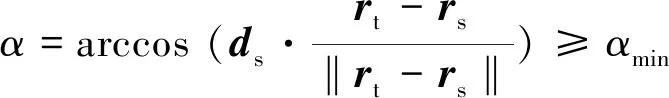
(7)

式中：ds为太阳方向单位矢量；rs为子航天器位置矢量；rt为目标航天器位置矢量。

2)子航天器末端和目标的相对速度‖vt-vs‖小于上限Δvmax，如果大于该上限，子航天器相机的伺服机构可能无法保持对目标定向。

3)子航天器末端和目标的相对位置‖rt-rs‖小于上限ε，确保子航天器和目标在一定距离范围内，可以实现巡察任务。

轨道机动约束具体如下：

1)机动过程中平台和子航天器的轨道高度h大于下限hmin；

2)子航天器机动大小‖Δvs‖小于上限Δvs_max；

3)子航天器机动在平台轨道面外的分量占面内分量的百分比低于上限Pmax，以确保共面机动；

4)平台单次和总的机动能力小于一定上限。

3.2 满足巡察约束的窗口筛选计算模型

对于每一个候选巡察时刻，遍历平台机动大小和子航天器释放机动时刻，评价每一种机动方案能否满足单次巡察任务的所有约束条件，如果满足则终止遍历，认为该候选时刻为可行窗口；如果不满足则一直遍历直到变量穷尽，认为该候选时刻为不可行窗口。

遍历搜索分两层进行，外层遍历第一次机动大小Δv1，内层遍历子航天器释放机动时刻ts，遍历的范围如式(8)和(9)所示。

0≤Δv1≤Δvp_max

(8)

(9)

式中：Δvp_max为平台单次机动上限；tf为巡察窗口时刻；Tt为目标卫星的轨道周期。

由于高精度模型的计算速度较慢，模型分为低精度和高精度计算两个步骤。首先进入低精度计算，如果得不到满足约束的结果，直接退出计算流程；如果遍历得到满足约束的可行窗口，进入高精度计算。低精度计算考虑J2长期项的解析轨道模型，高精度计算采用摄动轨道积分模型，末端Lambert问题的求解算法都考虑相应模型，并按照补偿法的思路对瞄准点迭代修正。

为提高遍历计算速度和精度，无论是在低精度还是高精度计算中，都分为粗搜索和细搜索两个部分。粗搜索中得到一种满足约束的方案，进入细搜索，否则一直粗搜索。细搜索的搜索范围为粗搜索结果的附近区间，类似于一个局部再搜索。整个计算的流程如图4所示。

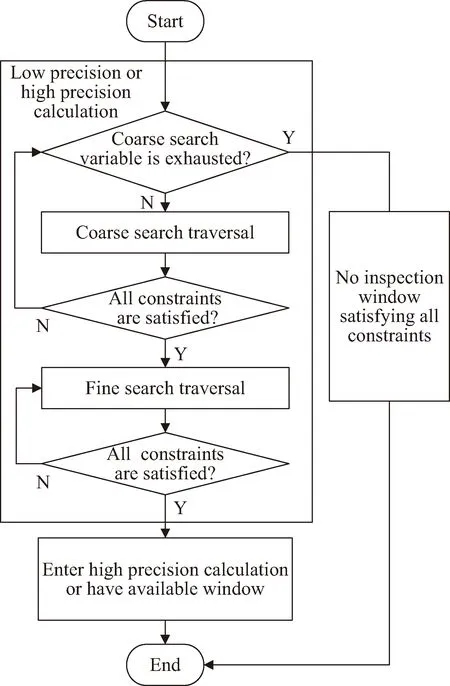
图4 满足巡察约束的窗口筛选计算流程Fig.4 Flow chart of window screening calculation satisfying inspection constraints

在粗搜索中，外层在遍历范围内从小到大平均遍历n1次，内层在遍历范围内从大到小平均遍历n2次。在细搜索中，外层在粗搜索结果附近范围内从小到大平均遍历n3次，内层则和粗搜索一样，在同样范围内遍历n2次。当Δv1大于平台剩余速度增量的一半或ts小于第二次机动时刻t2，不满足任务要求，终止遍历。

3.3 基于贪婪搜索和多轮规划的任务规划方法

基于贪婪搜索的策略，以推进剂最省或任务时间最短为指标，优化多星巡察中的任务分配方案和巡察次序。由于推进剂最省和任务时间最短规划方法相似，以推进剂消耗最省为例，对贪婪搜索计算流程进行说明，任务时间最短规划方法不再赘述。基于贪婪搜索的策略，采用多轮规划的解决思路，计算的总流程如图5所示。

图5 贪婪搜索和多轮规划计算流程Fig.5 Flow chart of greedy search and multi-round planning

具体分为如下6个步骤：

1)在当前起止时间范围内，计算所有可用平台和待巡察目标指派关系的全部可行窗口。

2)对于每个指派关系，可能包含多个满足约束的窗口，选择其中最节约推进剂的一个，作为该指派关系的巡察方案。

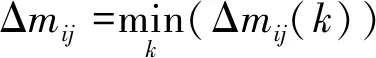
(10)

式中：Δmij(k)为平台i巡察目标j的可行窗口k。 如果没有可行窗口，则该指派关系对应的推进剂消耗数值记为正无穷，如式(11)所示。计算所有指派关系的最省推进剂方案，最终得到一个用于任务分配的决策表格，如表1所示。

Δmij=+∞

(11)

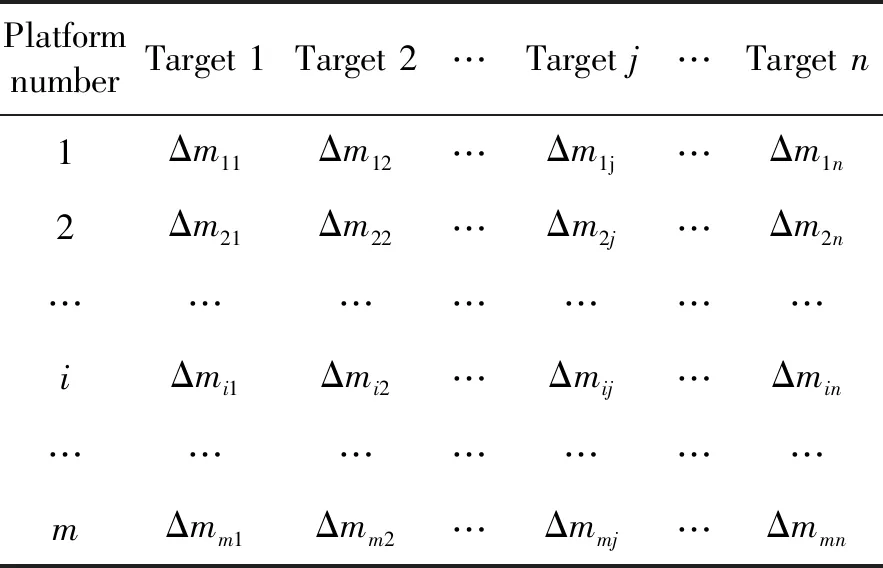
表1 巡察任务分配决策表格

3)按照贪婪搜索的策略，挑选其中最节约推进剂的巡察方案，并记录对应的行和列。

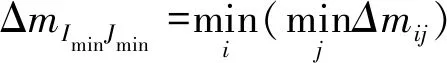
(12)

式中：Imin、Jmin分别为推进剂最省指派关系对应的行号和列号。

完成这一次的搜索，将对应的行和列删除，在数值处理上为将对应指派关系的推进剂消耗数值置为正无穷，如式(13)所示。

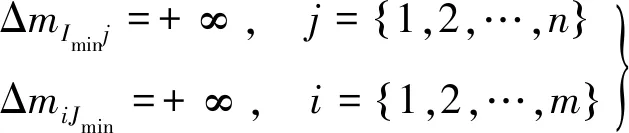
(13)

4)重复步骤3，直到决策表格为空，也就是所有数值都为+∞，完成一轮任务规划。

5)更新平台和目标的轨道、质量和子航天器数量等状态信息，将巡察过的目标和没有子航天器或推进剂的平台去除，以最后一个巡察任务完成时刻为这一轮任务的结束时间。

6)重复步骤1～5，进行多轮次的规划，直到待巡察目标数或剩余平台数或成功指派数为0，得到总任务规划方案。

4 算例分析

4.1 参数配置

任务的起始历元为2020年8月1日04:00:00.0(BJT)，每一轮窗口计算的最小时间和最大时间为2 h和24 h，巡察星每次转移前的时间为0.5 h。子航天器的总机动能力为350 m/s，基于共面机动的假设，其机动面外分量占面内分量的上限不得超过10%，其余参数配置如表2所示。

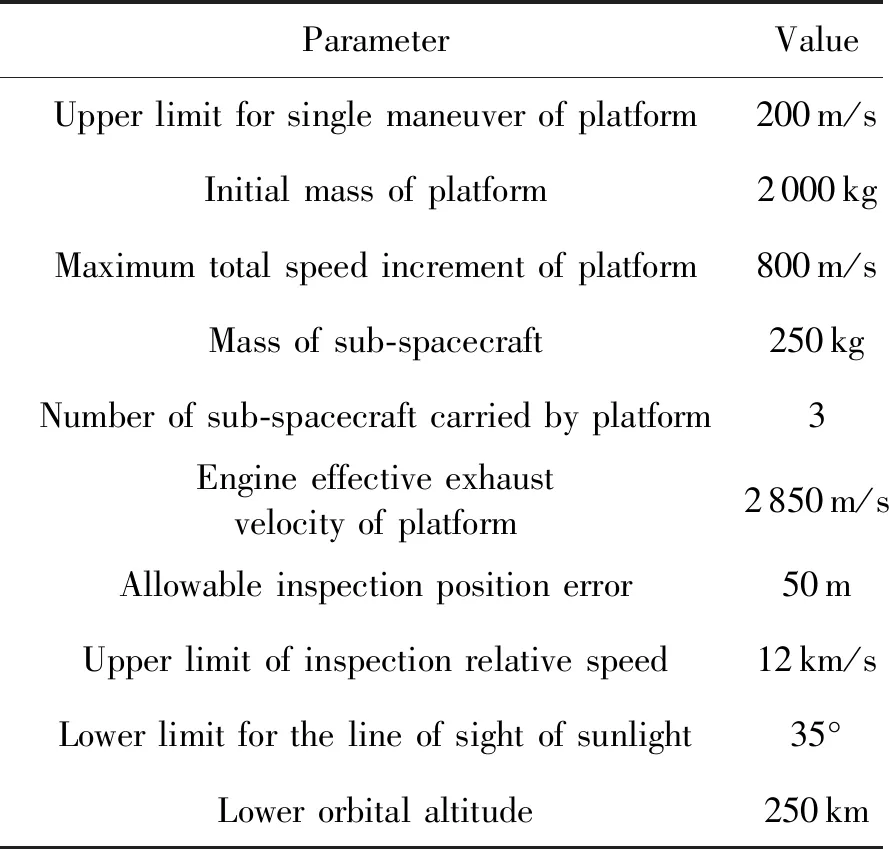
表2 任务参数

一共有4个平台位于近地近圆轨道上，半长轴都是7 078.14 km，偏心率都是0.001，轨道倾角都是98.193°，升交点赤经均匀地分布在空间中，分别为52.970°，142.970°，232.970°，322.970°，近地点角距和真近点角都是0°。9个目标卫星位于太阳同步轨道，其轨道参数如表3所示。

遍历的次数对计算的速度和准确性影响很大，分为低精度和高精度给出相应的参数配置：在低精度中，n1=60，n2=100，n3=10；在高精度中，n1=30，n2=10，n3=5。摄动轨道积分考虑了2×2的JGM3非球形引力场模型、NRLMSISE-00大气阻力模型以及太阳和月球的三体引力模型。

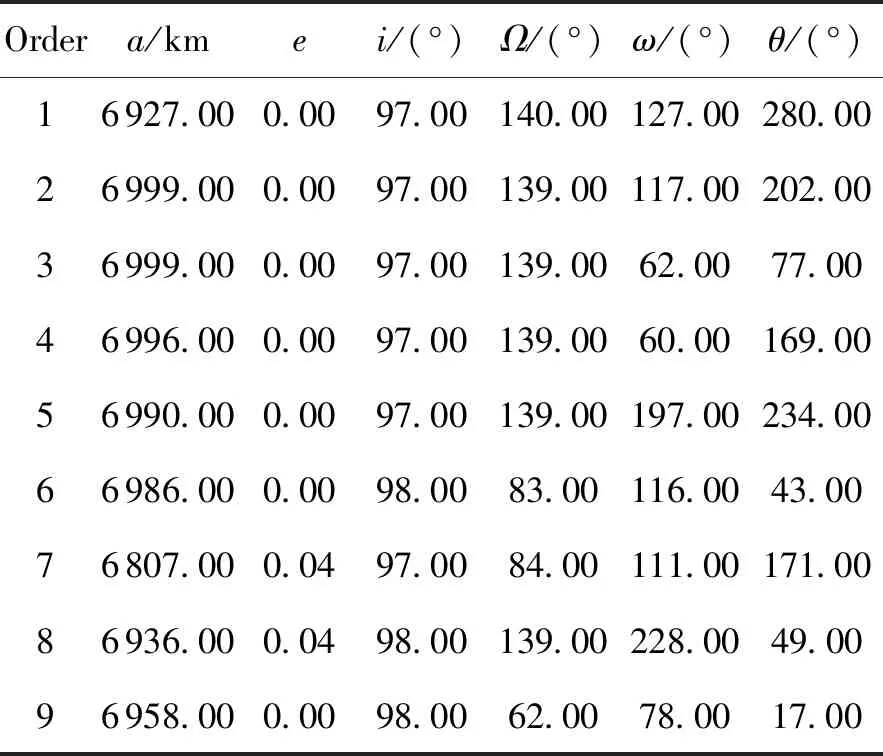
表3 目标参数

4.2 推进剂和任务时间最优规划结果

首先给出推进剂最省计算结果，分为三轮进行任务规划，在第一、二和三轮规划中，可用平台数量都是4，可选择的巡察目标数量分别为9、6和3。由于平台4一直没有可行窗口，所以不进行展示，结果也只给出第一轮规划结果和最终总结果，如表4和表5所示，第二轮和第三轮规划结果不详细列出。推进剂最省计算结果为96.4 kg，任务的时间大约为67.59 h。接着给出任务时间最短的规划结果，如表6所示，推进剂消耗为949.7 kg，任务时间为17.69 h，不到一天时间完成所有巡察任务，且推进剂消耗也在可接受范围内。

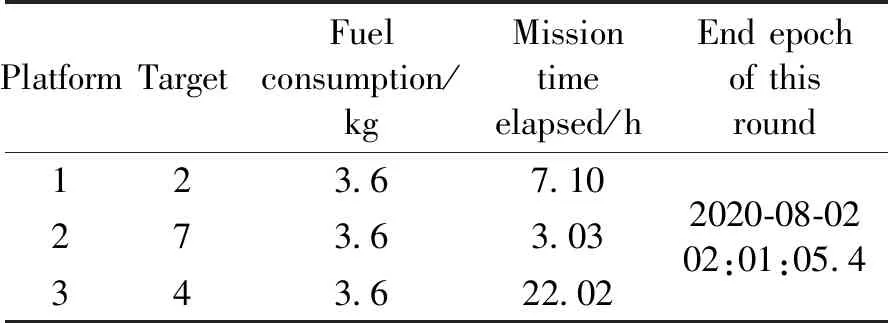
表4 推进剂最省规划第一轮结果

表5 推进剂最省解的结果

表6 任务时间最短解的结果

最后，以任务时间最短方案中的平台2为例，利用高精度轨道外推模型进行验证，其三维轨迹仿真结果如图6所示，位置矢量的分量数值是在J2 000地心惯性系下给出的。

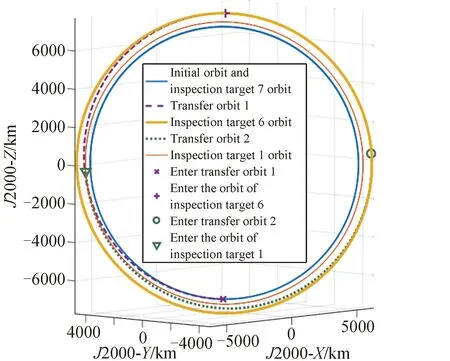
图6 任务时间最短方案中平台2轨迹Fig.6 Trajectories of platform 2 in the shortest mission time scheme

图7展示的是平台2和子航天器与目标7的相对距离曲线，平台释放子航天器后，子航天器经过一段时间的滑移，和目标卫星7的相对距离接近为0 km，完成巡察任务。而平台2则继续滑移，携带多个子航天器，依次对其他目标进行巡察。

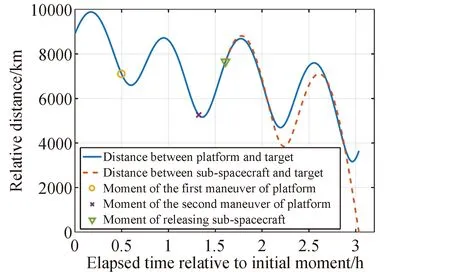
图7 平台2巡察目标7的相对距离曲线Fig.7 Relative distance curve of platform 2 inspection target 7

4.3 贪婪搜索算法和混合编码遗传算法对比

为了对比分析贪婪搜索算法和混合编码遗传算法的求解效率和优化效果，给出如下算例：可用平台只取前文算例中的前3个平台，目标数量还是9个，轨道参数不变。为了降低问题的求解难度，将轨道模型改为二体模型，其余参数和条件不变。

采用混合编码遗传算法[14]进行对比计算，设计变量包括任务分配、交会次序、所有目标的时间窗口选择、第一次机动大小和释放子航天器时刻。其中任务分配和交会次序变量按照整数编码的规则进行交叉变异等操作，时间窗口选择按照实数编码的操作进行，最后再进行取整。第一次机动的大小和释放子航天器时刻按照实数编码的规则进行操作。由于任务较为复杂，固定任务分配为每个巡察平台巡察目标数量相等，这样也可以避免某个特定的平台巡察过多目标卫星的情况。

遗传算法的实数编码的参数界限如下：时间窗口选择的下界为1，上界为当前任务初始时刻起算2 ～24 h的时间范围内最大窗口数；第一次机动大小的下界为0，上界为单次航天器机动能力上限和平台剩余速度增量一半中的最小值；释放子航天器时刻的下界为第二次机动时刻和巡察时刻倒推一个巡察星轨道周期的最大值，上界为巡察时刻倒推1/4巡察星轨道周期。遗传算法的整数实数交叉概率为0.8，变异概率为0.7，锦标赛方法中每次参加竞赛的个体数量为3，对于所有的约束采用罚函数处理。贪婪搜索算法的遍历次数采用低精度模型的参数，在计算二体模型后，如果得到可行解，则直接返回，不进入高精度模型进行计算。

在配置为Intel(R) Xeon(R) E5-2690 v4 (2.6 GHz, 64 GB)的计算机上进行计算，分别以推进剂消耗最省和任务时间最短为目标进行求解，混合编码遗传算法按照不同的种群规模和进化代数分为5组，每组都重复进行20次，取其中最好的一个作为最终结果。对于没有结果的情况，计算时间取最短的一组作为对比。

如表7所示，贪婪搜索算法在4 min左右就可以得到较优的结果，而混合编码遗传算法在计算时间较短时，无法得到可行解；当计算时间约是贪婪搜索算法的47倍时，可得到满足所有约束的解；当计算时间达到贪婪搜索算法的约227倍时，优化效果仍然不如贪婪搜索算法。结果表明，对本文仿真场景，贪婪搜索和多轮规划方法的优化效果稍优于混合编码遗传算法，而且计算效率得到了较大提升，是遗传算法的约227倍。

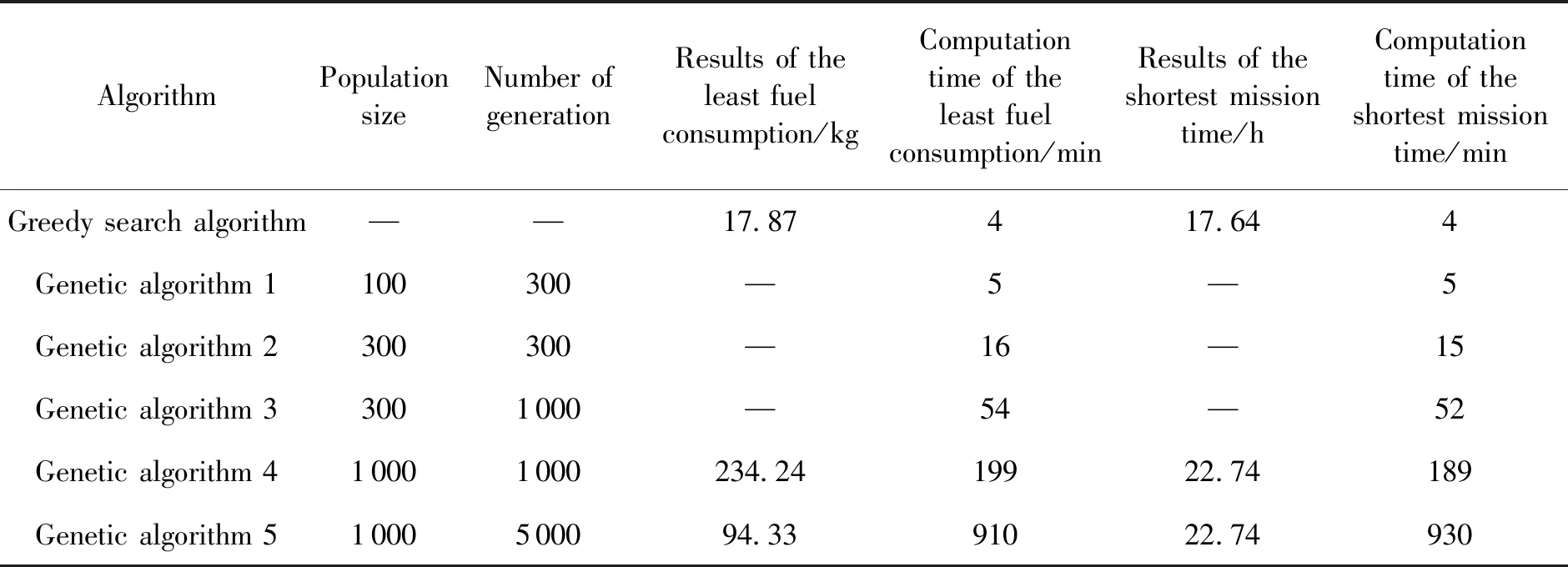
表7 两种算法的优化结果与计算时间对比

如图8所示，采用种群规模为1 000、进化代数为5 000的混合编码遗传算法得到推进剂消耗进化曲线，纵坐标为目标函数，记录的结果为每一代最优解。前844代中没有满足约束的解，所以曲线没有对应的数值。在第845代时算法收敛到了一个可行解范围内，并不断进化，得到最终结果。

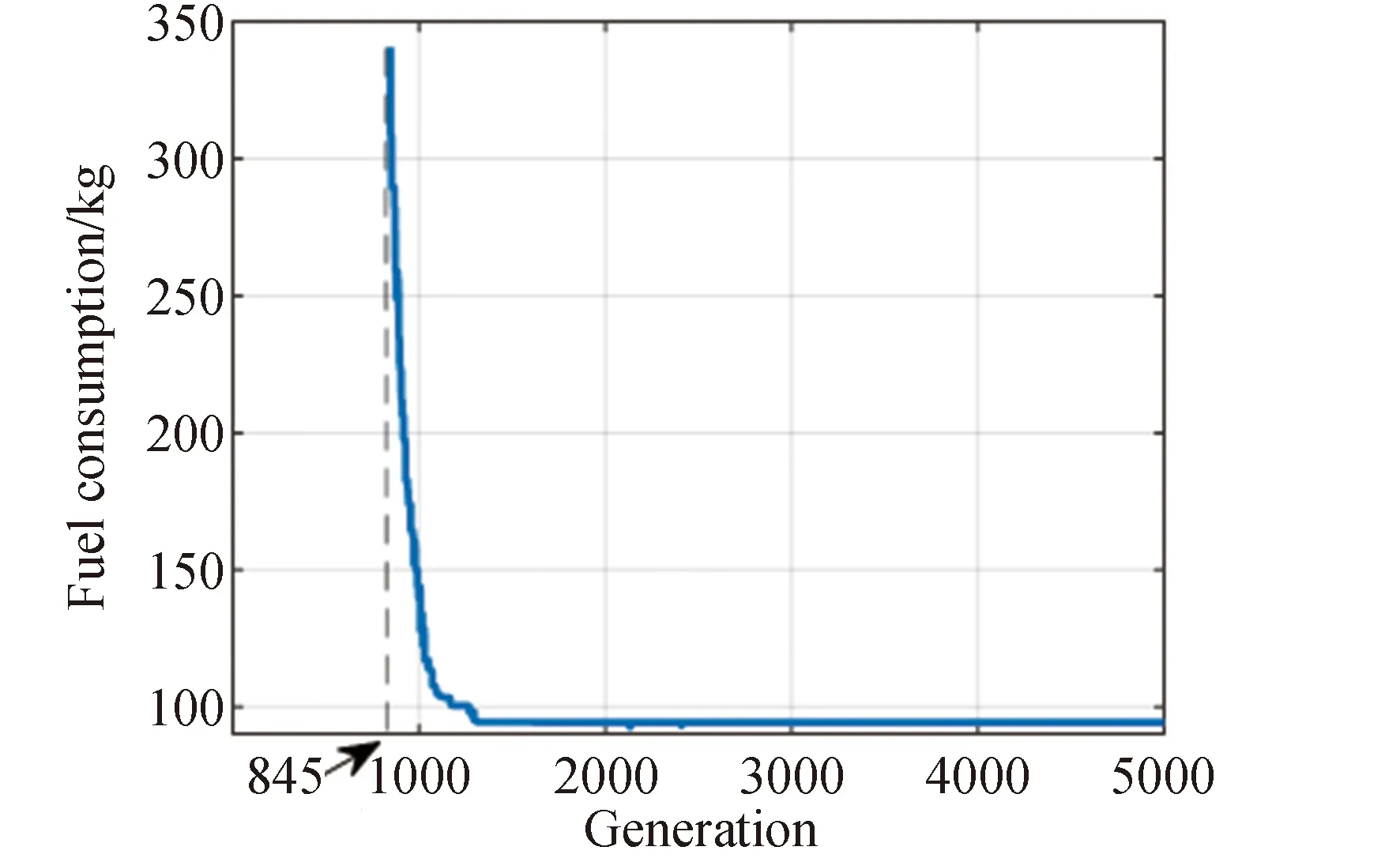
图8 推进剂消耗进化曲线Fig.8 Evolution curve of fuel consumption

传统的优化算法在面对多约束时一般采用罚函数的方法求解，随着问题的规模和约束条件数量的增加，问题的求解难度会大大增加，而采用贪婪搜索的算法可以分批单独处理多种约束条件，降低了问题的求解难度，快速得到一个较优的可行解，具有稳定高效的特点。

5 结论

本文研究了考虑多种约束条件的多星快响任务规划方法，具体内容为多平台对多目标卫星在短时间内的巡察任务规划。提出满足巡察约束的窗口计算模型，基于贪婪搜索和多轮规划的方法，给出任务分配和巡察次序确定模型。该方法降低了由多种约束条件难满足所带来的问题求解难度，有效解决了推进剂最省或任务时间最短的任务规划问题，得到以下两个结论：

1)在当前条件下，4个近地平台巡察9个近地轨道目标，任务时间最短方案为不到1天，推进剂消耗满足所给定的约束条件。

2)在本文仿真场景下，贪婪搜索算法结果稍优于混合编码遗传算法，计算效率是后者的约227倍，表明贪婪搜索算法可以分批处理较多的约束，满足实际工程需求。

由于贪婪搜索算法带来的局限性，可能会出现局部最优的情况，以后需要研究带有一定随机性的搜索策略，得到更接近全局最优的结果。