基于转矩模型和改进MOPSO的永磁球形电机磁极优化

李国丽， 孙涛， 周睿,3， 王群京， 李文爽

(1.安徽大学 电气工程与自动化学院，安徽 合肥 230601；2.安徽大学 高节能电机及控制技术国家地方联合实验室，安徽 合肥 230601；3.安徽大学 工业节电与用电安全安徽省重点实验室，安徽 合肥 230601；4.安徽大学 工业节电与电能质量控制安徽省级协同创新中心，安徽 合肥 230601)

0 引 言

随着工业自动化的不断发展，多自由度球形电机以其体积小、运动方式灵活、动态响应速度快的优点引起了广大学者的关注和研究，在机器人关节、电动陀螺、全景摄像云台等领域具有广泛的应用前景[1-3]。永磁球形电机在能量密度、运行效率和可控性上具有极大优势，是球形电机研究的重要方向[4]。球形电机的磁场在三维空间分布和运动，转子转矩计算比传统单自由度电机复杂得多，给电机设计阶段的结构参数优化带来困难。

ROSSINI L等利用球谐函数解析模型分析了几种不同结构参数对电机径向磁密的影响，在一组规范的要求下进行参数组合寻优[5]。HE J等以定子线圈内外径差、线圈高度和圆柱形永磁体的半径、厚度为自变量，应用田口法仿真了不同变量水平下的磁密和转矩，结合响应面模型获得了电机的最优结构参数组合[6]。常规的优化设计方法先分别分析单个参数对电机性能的影响，然后再主观选取一个结构参数组合，这种方法得到的优化结果能满足预定需求，但并非电机结构参数优化的全局最优解，而且忽略了不同参数之间制约和联系。为了实现永磁球形电机结构参数的全局精确优化，引入智能算法是必要的。JIE Z等用有限元软件模拟的样本点导出了球形电机转矩的支持向量机模型，然后用遗传算法对结构参数进行了优化，提升了转矩密度[7]，不足的是仿真样本点拟合模型的精确度欠优。信建国等利用解析模型对气隙磁场的基波幅值和波形畸变率进行了多目标优化，并比较了不同磁化方向的区别[8]。YAN L等提出了安培转矩和齿槽转矩的混合建模方法，以与期望的最小误差平均值为目标进行了粒子群参数优化[9]。

目前球形电机转矩优化的目标多在单个运动维度上选取，本文旨在电机自旋和俯仰两个运动维度上做优化工作，表征球形电机输出转矩的整体情况。以一种等效面电流磁密和洛伦兹力转矩的解析模型为基础,改变永磁球形电机的转子磁极大小，对自旋转矩幅值和俯仰转矩幅值进行多目标粒子群优化(multi-objective particle swarm optimization, MOPSO)，并对算法进行改进，从前沿面的收敛性和分布性上分析了改进MOPSO的提升性能。最后，从优化的前沿面上均匀选取部分点，分析转矩分布情况并从中选出电机优化的最终解。

1 永磁球形电机及其转矩模型

1.1 电机原型

研究的电机原型如图1所示。转子球半径65 mm，永磁磁极为16个边长为17 mm的正方体，标准的八极Halbach[10]阵列分布在赤道线上。定子壳内径66.5 mm。电机可任意自旋，最大俯仰角为±30°。24个铝芯线圈沿赤道线和南纬30°线均匀分布，线圈内径5 mm，外径15 mm，高13.5 mm，匝数500。

图1 电机原型

1.2 转矩模型

根据安培分子环流假说，均匀磁化的永磁体内部分子作用相互抵消，从外部来看，仅与磁化方向平行的侧表面上的束缚电流产生磁场[11]。

矩形永磁体磁密计算示意图如图2所示。三维正交坐标系的原点位于永磁体的中心，永磁体的长、宽、高分别为Lx、Ly、Lz，沿Z轴正方向充磁。永磁体可等效为平行于Z轴的4个侧面上的表面束缚电流，对外界产生磁场，电流的方向符合右手定则。在高度为h处，取一块厚度为dh且与磁化方向垂直的薄片，定义其四边首位相接的电流段I1、I2、I3、I4，在I1段取一微元I1dl[12]。取永磁体外一点P(x,y,z)，作P点到I1线段的垂线D，垂足为U。电流微元至P点的连线与I1方向的夹角为α。假设电流微元I1dl至P点的矢量为r，由毕奥-萨伐尔定律[13]得

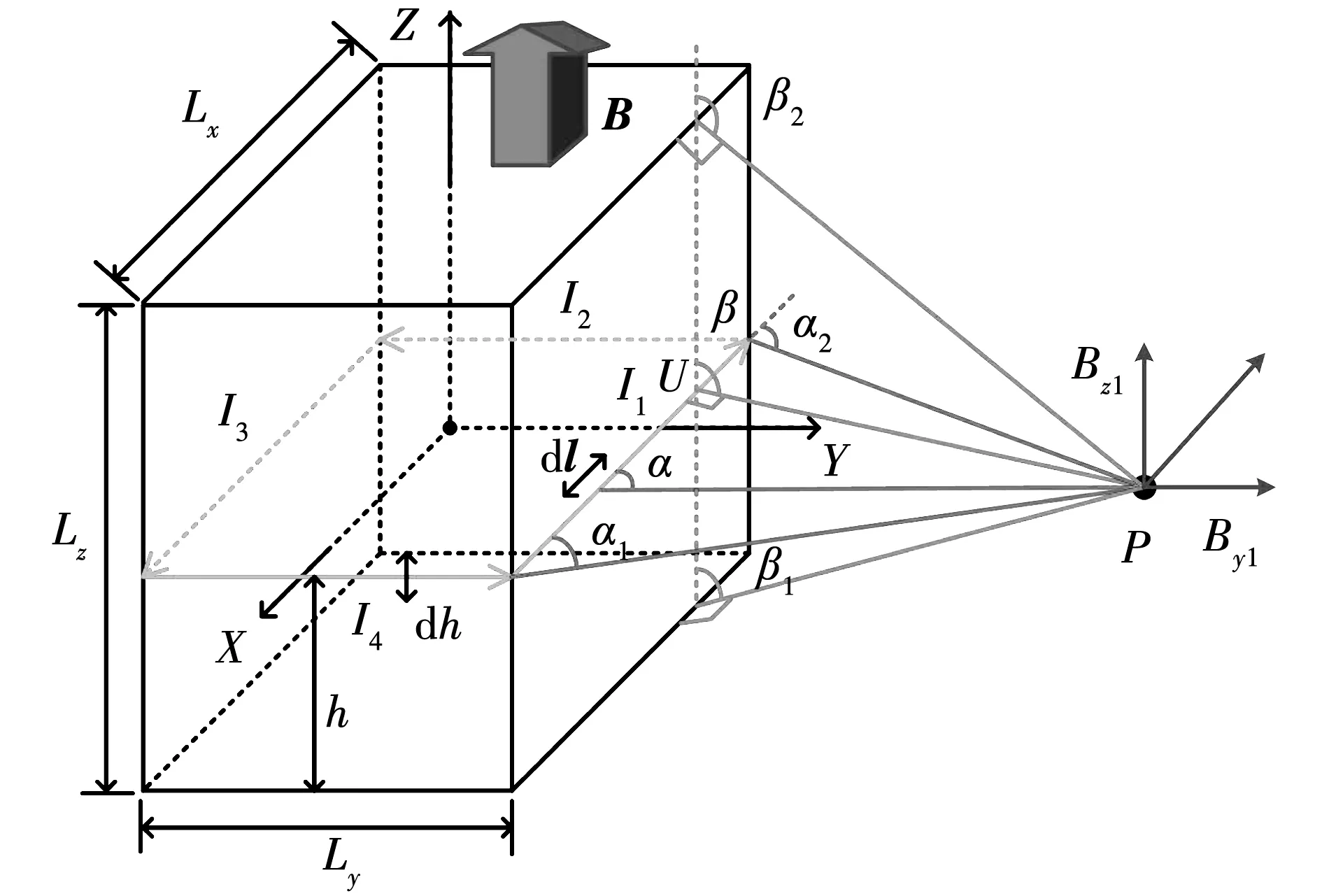
图2 矩形永磁体磁密计算示意图

(1)

由电流段I1起点至终点，α由α1增到α2，可得电流段I1在P点的磁密BI1。作经过垂足U的Z轴平行线，由U指向P的垂线D与Z轴正方向夹角为β。对dh在整个面上积分，得β≥0时，整个右侧面在P点的磁密[12,14]为：

(2)

同理，可以求出其他3个侧面上的束缚电流在P点的磁密。原型电机转子磁极为永磁材料，定子线圈采用无铁心设计，可认为整个电机分析区域是线性磁路。结合叠加定理就可以求出整个矩形永磁体在三维空间中点P的磁密分量。依据空间中P点在电机转子各永磁体的相对位置，可以分别求出在各永磁体局部坐标系下的P点磁密。经过平移和旋转操作，即可叠加得到转子全局坐标系下空间P(xr,yr,zr)点的磁密Bxr、Byr、Bzr[14]。

根据作用力与反作用力的原理，想要求解转子在通电线圈作用下的转矩，可以反向求解通电线圈在转子磁场中所受的转矩。

依托转子旋转坐标系和定子静止坐标系之间的9个坐标轴夹角，可以将转子坐标系下P点的磁密转换为定子坐标系下的磁密Bxs、Bys、Bzs[14]。

应用三维剖分的方式将定子线圈划分为大量的小块，各小块被看作点分别计算其转矩。根据洛伦兹力的积分形式可得线圈上各点的洛伦兹力分量，表达式为：

(3)

计算点处电流向量J分解为：

(4)

式中：lon、lat分别表示计算点所属线圈在定子坐标系下的经度和纬度；θ为线圈圆环截面上计算点的位置角[14]。

综上所述，电机原型单个线圈通电情况下的转子转矩在定子坐标系下的分量为：

(5)

式中x、y、z为计算点在定子坐标系下的坐标值，表征洛伦兹力作用的力臂。多个线圈同时通电工作时，只需分别计算各个线圈的贡献，然后叠加即可。

1.3 仿真与实验验证

为验证上节转矩模型的有效性，对图1的电机原型进行Ansys建模仿真和实验验证。

设置2种运动轨迹，分别监测自旋和俯仰方向的转子转矩分布：1)转子由-45°至45°绕z轴自旋运动，期间不存在俯仰和倾斜运动；2)转子由-30°至30°绕y轴俯仰运动，期间不存在自旋和倾斜运动。

图3为球形电机实验平台，将本文研究的电机原型置于测试台架中，输出轴与台架联动。测试台架由1个固定支架和2个旋转支架组合工作，每个旋转方向配备1个位置传感器和1个静态扭矩仪测量转子旋转角和转矩；电机驱动电路由24个STM32芯片控制的DC恒流源电路集成，在上位机LabVIEW软件中构建通电控制画面，实现对球形电机的灵活控制。为了减小电机实验中摩擦力和测量误差造成的转矩解析值与实验值之间的相对差距，对经纬度均为0的线圈给定3 A正向电流。

图3 电机实验平台

记录每个离散点的转矩输出值，与转矩模型解析值对比如图4所示。Ansys有限元软件的转矩仿真值与解析计算值基本一致；实验测量值整体偏小，主要由摩擦转矩造成。可见，转矩解析模型在保证精确度的情况下，在可塑性、快速性和可靠性上具有极大优势。

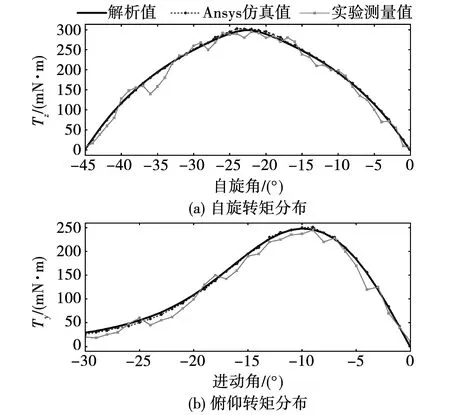
图4 解析、仿真、实验值对比

2 改进的多目标粒子群磁极优化

电机矩形永磁体的尺寸发生变化时，三维耦合磁场的变化是非常复杂的，自旋转矩和俯仰转矩经常出现相悖的变化趋势。本文研究的多目标优化问题是以电机原型为基础，转子球半径保持不变，改变矩形永磁磁极尺寸，在自旋转矩幅值和俯仰转矩幅值这两个相互冲突的目标之间去衡量取舍。将主磁极和过渡磁极的尺寸区别开来，可以更灵活地在转子球内分配位置空间，更恰当地发挥过渡磁极的单边特性。

设置6个自变量：l1、w1、t1、l2、w2、t2，其中的l、w、t分别对应图2中的Ly、Lx、Lz，下标1、2分别代表主磁极和过渡磁极。对位于零经、纬度的线圈施加1 A的电流，假设转子从初始位置反向自旋45°，自旋转矩幅值Tzmax作为电机自旋方向上的转矩评判指标；假设转子从初始位置反向俯仰30°，俯仰转矩幅值Tymax作为电机俯仰方向上的转矩评判指标。

2.1 永磁体结构参数约束

转子球半径固定不变时，球内矩形永磁体的大小发生变化，需对永磁体的结构参数做出约束。磁极尺寸约束如图5所示，图5(a)示意了一对相邻的主磁极(左)和过渡磁极(右)，与电机原型对应，永磁体的中心都位于XY平面，即球形转子的赤道所在平面。A1、A2分别为主磁极和过度磁极的外表面中心。图5(b)为图5(a)的俯视图，也就是转子球赤道所在的面。其中D1、D2分别为主磁极和过度磁极内表面的中心。

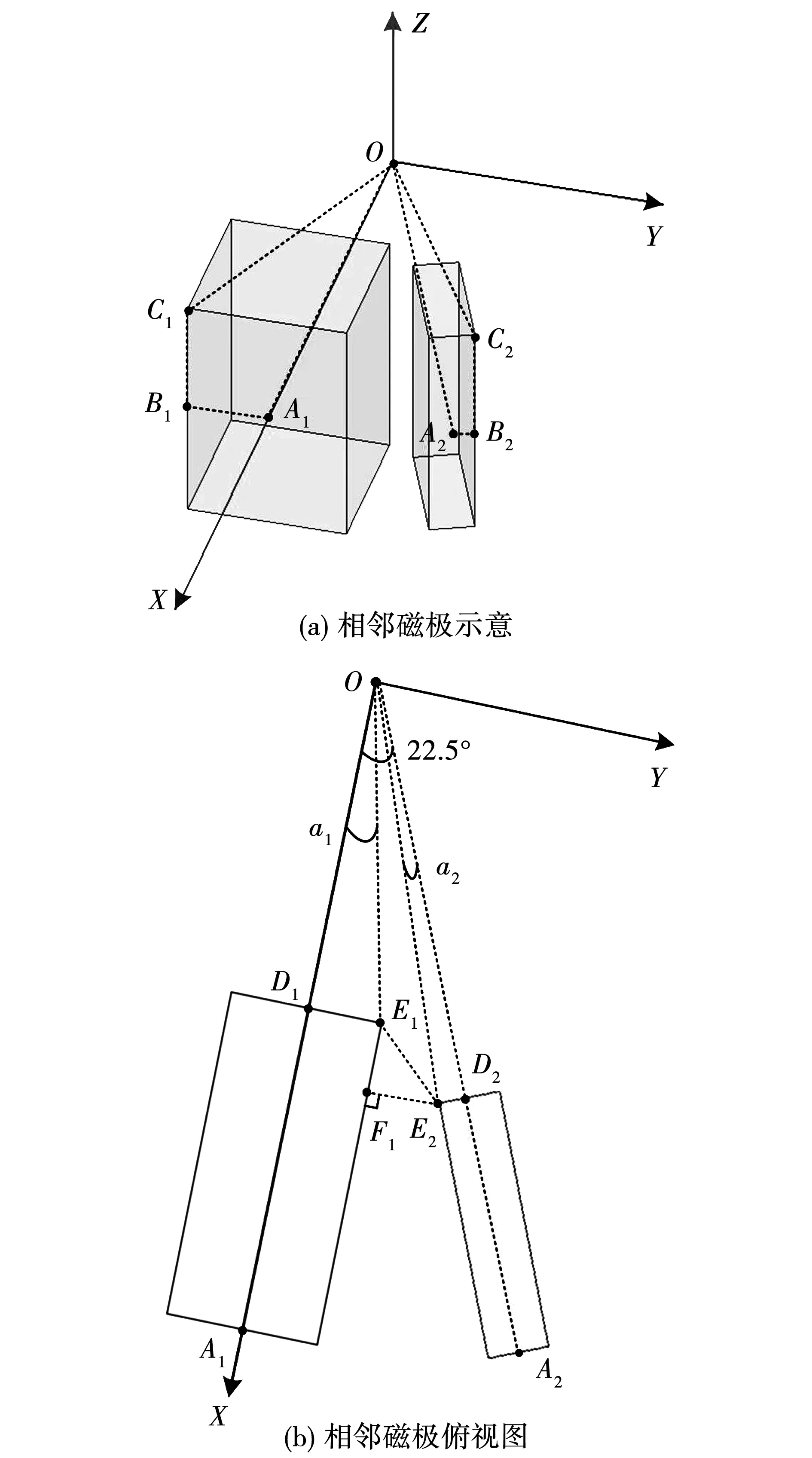
图5 磁极尺寸约束

为了充分发挥永磁体的作用，永磁体与定子线圈的距离应尽可能小。由于永磁体为长方体，磁极上必定存在一个离转子球面最近的点，即图5(a)中的C1和C2。考虑加工需求，永磁体与转子球面之间需预留一定的距离，原电机理论上为0.863 mm，为了降低加工难度，预留出1 mm。转子球半径65 mm,设计永磁体离转子球面最近距离64 mm，即lOC1=lOC2=64 mm，其中lOC1、lOC2分别为线段OC1、OC2的长度，后文中类似表述不再说明。设置磁极距球心最近距离lOD1、lOD2大于5 mm。

除了各永磁体本身在转子球面和球心之间的约束，还要保证相邻两个磁极不会出现重合，规定相邻磁极之间最小距离d不能小于1 mm。

如图5(b),假设d为过渡磁极的E2到主磁极右侧面垂线的长度，即lOE2cos(22.5°-a2)≥lOD1时，有

d=lOE2sin(22.5°-a2)-0.5l1。

(6)

相反地，如果d为主磁极的E1到过渡磁极侧面垂线的长度，即lOE1cos(22.5°-a1)≥lOD2时，有

d=lOE1sin(22.5°-a1)-0.5l2。

(7)

综上所述，优化问题的自变量参数约束条件为：

(8)

其中：

考虑加工工艺的要求，自变量的搜索范围取2～40 mm。

2.2 粒子群算法中的变量约束处理

针对本文的磁极约束优化问题，在经典粒子群算法[15]中嵌入惩罚函数[16]：对目标函数和表示约束条件的惩罚函数赋予权重，组合出带参数的增广目标函数，把约束问题转化为无约束问题进行求解。

构造评价函数为：

(9)

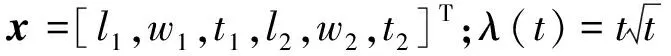
K(x)=θ(q(x))q(x)α。

(10)

由式(8)定义：

q(x)=max{0,5-lOD1,5-lOD2,1-d}。

(11)

(12)

惩罚函数中系数θ(q(x))和级数α分级取值，目的是让可行域附近的部分不可行解也参与到优化进程中，保持参与搜索粒子的多样性，使得粒子更快地接近更优位置。在粒子离可行域较远时，惩罚系数和级数很大，其实就相当于直接剔除不可行解。因研究的电机转子永磁体为单层分布，俯仰转矩整体上比自旋转矩数值小，故惩罚因子另赋系数0.6。

2.3 应用网格密度的MOPSO

在粒子群算法的具体搜索过程中，同时计算2个目标值，应用Pareto理论[17]得到反应F1(x)和F2(x)分布情况的前沿面PF。

设置一个非劣解集A，即搜索过程中的最优解集。将A内所有粒子在目标空间中的分布划分为N×N个网格，网格数量N随非劣解集中解的个数自适应变化，每个网格里包含的粒子个数表示相应粒子的密度，根据所有网格的密度信息来确定gbestx。

网格及其密度信息的获取过程如下[18]：

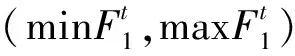
2)计算网格的模：

3)遍历At集中的粒子，计算其所在网格编号。粒子i的网格编号为

4)计算网格的密度信息。

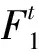
非劣解集A的更新与粒子群的搜索是同步进行的。假设算法寻找到一个新解x′,如果A中有粒子占优x′，则直接返回A；如果x′占优A中的某些粒子x1、x2、…、xq，则A=A/{x1,x2,…,xq}∪{x′}；如果x′与A中所有粒子都互不占优，则A=A∪{x′}。

为了避免非劣解集A容量过大,给A设定一个最大容量Mn。若A已达到最大容量，在密度最大的网格里以轮盘赌的方式随机剔除一个解，然后再进行更新。

pbestx的确定方法为:假设算法寻找到一个新解x′，若x′占优旧解,则pbestx取x′；若旧解占优x′,则pbestx保持旧解不变；若x′与旧解互不占优，则随机选一个为pbestx。

gbestx的获取方法为：计算A中粒子的密度信息；在密度最小的网格里随机选取一个粒子作为gbestx。

2.4 改进的MOPSO

2.4.1 引入拥堵距离

2.3节的MOPSO算法中应用网格密度法解决了算法迭代过程中全局最优解gbestx的权衡选取问题，使粒子朝分布稀疏的区域附近运动。但过程中的前沿依然会出现明显的空隙，当密度最小的网格存在多个时，简单随机选取的方式可能会错过实际分布最稀疏的粒子。网格密度示意图如图6所示，非劣解集的目标空间中包含13个点，各目标划分为5个网格，其中密度为1的网格有C点和极点pA，如果gbestx随机选择到C点,将违背粒子群向非劣解集中稀疏区域搜索的原则。为了加速前沿空隙的消失进程，对算法的分布性做如下改进：

图6 网格密度示意图

假设F为非劣解集在目标空间中的任意一点，其拥堵距离定义为

crowd_F=max(lFL,lFR)。

(13)

式中:L、R分别为与F相邻的左右两点；l表示两点之间的距离。

当非劣解集中最小密度网格存在多个或最小密度网格内有多个粒子时，计算对应粒子的拥堵距离，取拥堵距离最大的粒子为gbestx。如图6中，crowd_pA>crowd_C，选择pA的决策向量为gbestx。

2.4.2 引入凸点距离

迭代过程中粒子群朝分布稀疏的区域运动，前沿面在不断均匀分布的过程中也在逐渐向问题的“真实”前沿面靠拢。为了加速前沿面的收敛进程，引入凸点距离概念。

凸点距离示意图如图7所示，迭代过程中非劣解集在目标空间中有2个极值点FL和FR，Fk为前沿面上最凸的点，即离直线FLFR距离最远的点，定义该最远距离为凸点距离lFH。粒子群迭代时监测目标空间中的lFH，若其持续20代保持不变，则隔代选用Fk的决策向量作gbestx(忽略随着直线FLFR和Fk同时变化导致lFH不变的小概率情况)。

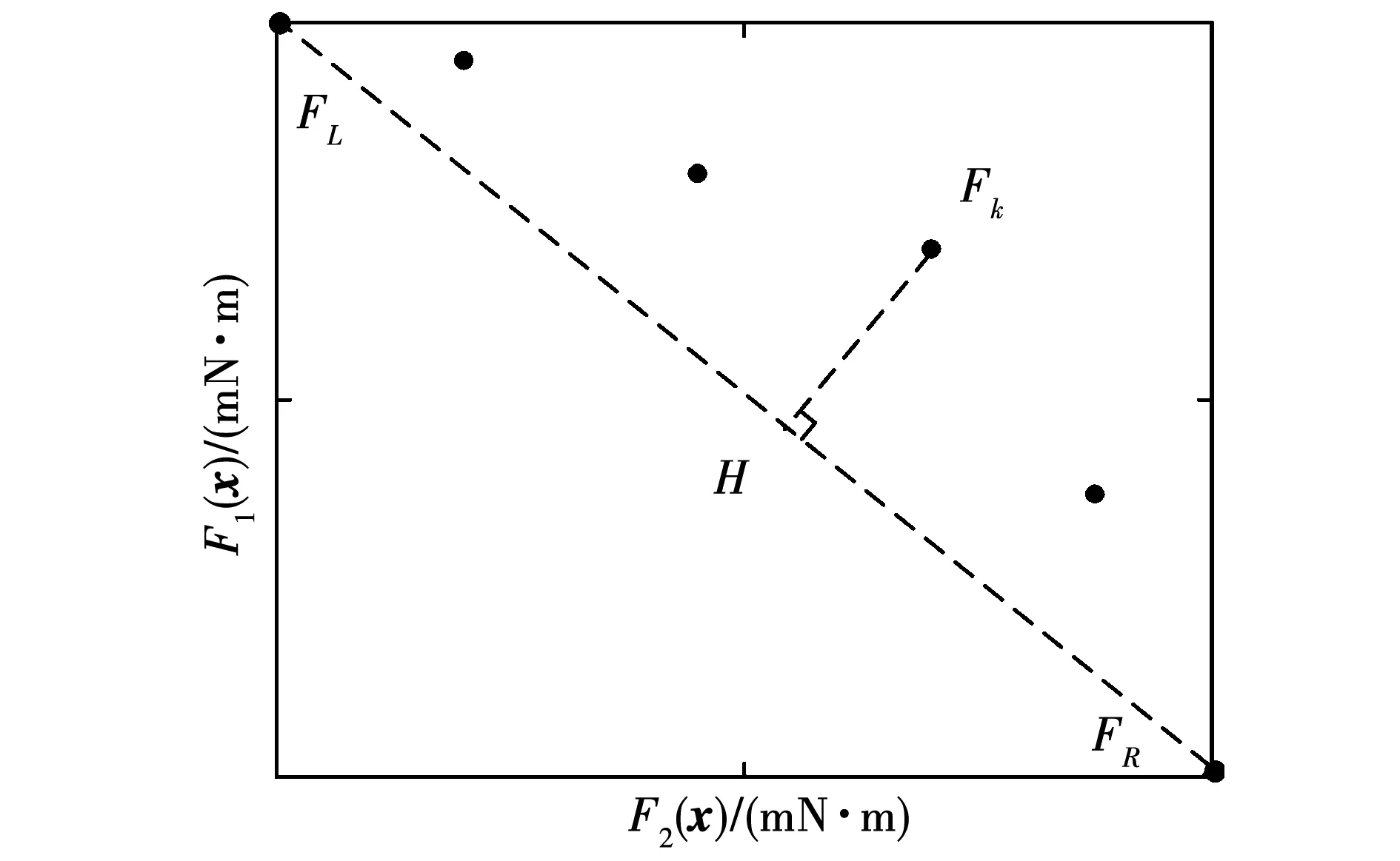
图7 凸点距离示意图

算法改进后，迭代过程中gbestx的选取策略如图8所示，能使前沿面更快地向“真实”前沿面靠拢，降低出现较大空隙的概率，得到分布更均匀的前沿。

图8 gbestx的选取策略

3 优化结果与分析

将MOPSO嵌入到转矩模型的计算程序中，搜索F1(x)和F2(x)的前沿面及对应永磁体尺寸。种群数量M取50，c1、c2取1.5，进化代数t设为1 000，惯性权重w=0.9-0.5/1 000t随进化过程逐渐减小；非劣解集的最大容量M取30，目标空间中网格个数N=Ceiling(NA/3)自适应变化，其中NA为非劣解集的粒子个数，Ceiling()为向上取整函数。

图9为算法改进前后得到的Pareto非劣解集前沿。可以看出，改进的算法优化结果比原算法前沿分布得更均匀，且收敛效果略优。本文研究问题的真实Pareto前沿面无法获取，然而算法改进前后找到的2个目标极值点相同，故以两目标极值点所在直线0.755x+y-196.751=0为基准，结合点到平面距离公式，定义迭代过程中的收敛性评判指标lk为：

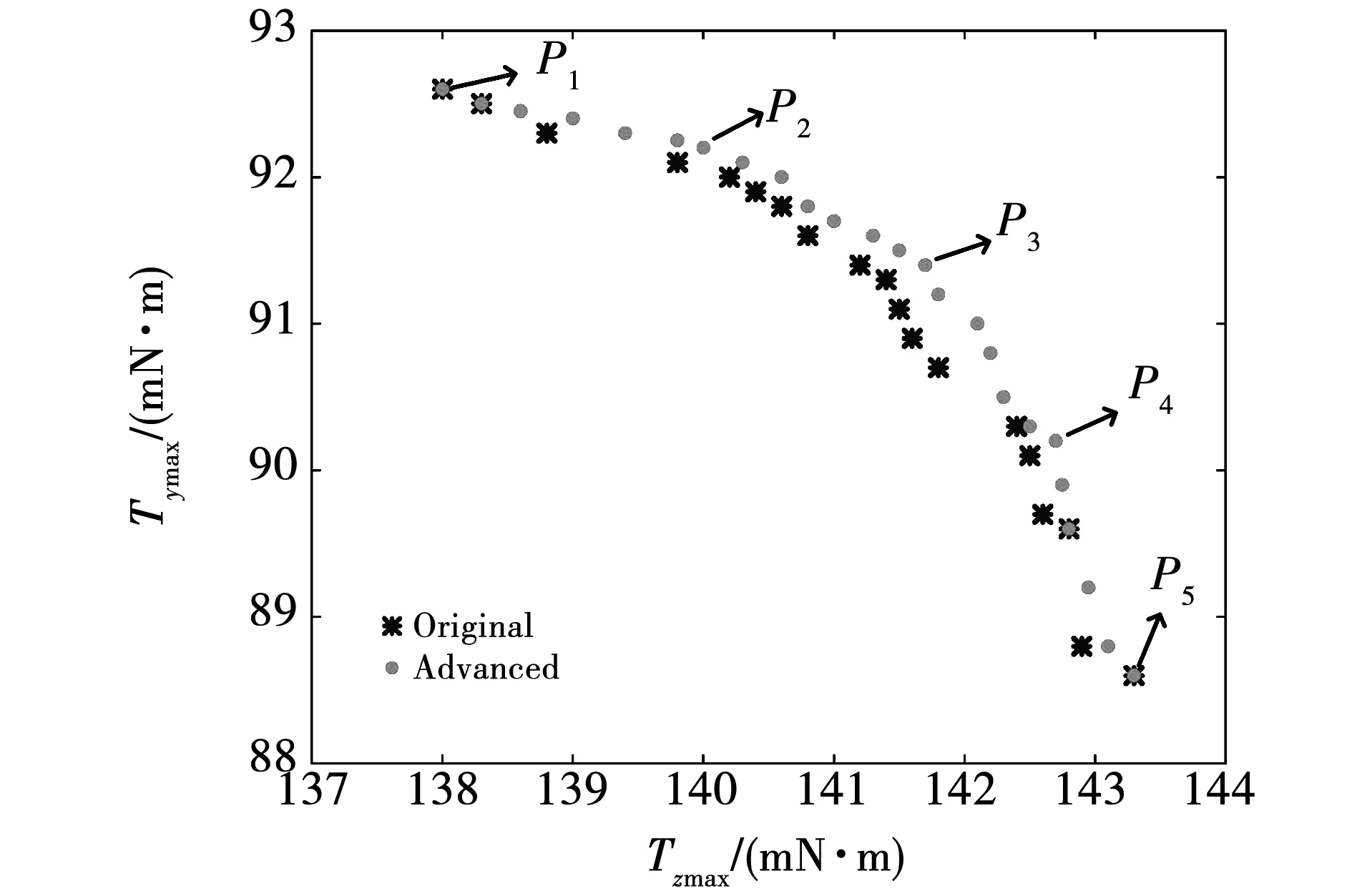
图9 算法改进前后优化的前沿面

lk=max{f(x1,y1),f(x2,y2),…,f(xNA,yNA)};

(14)

f(x,y)=(0.755x+y-196.751)/1.570。

(15)

式中：NA为非劣解集的粒子数；x和y指目标空间中非劣解的坐标。

lk越大，代表前沿面的收敛效果越好。计算每一代的lk如图10所示，可见引入的凸点距离刺激在迭代过程中起了明显作用。与原算法相比，迭代搜索过程中lk没有长时间停滞，收敛速度得到提升。具体参数如表1所示，其中拥堵距离选取最大的3个。

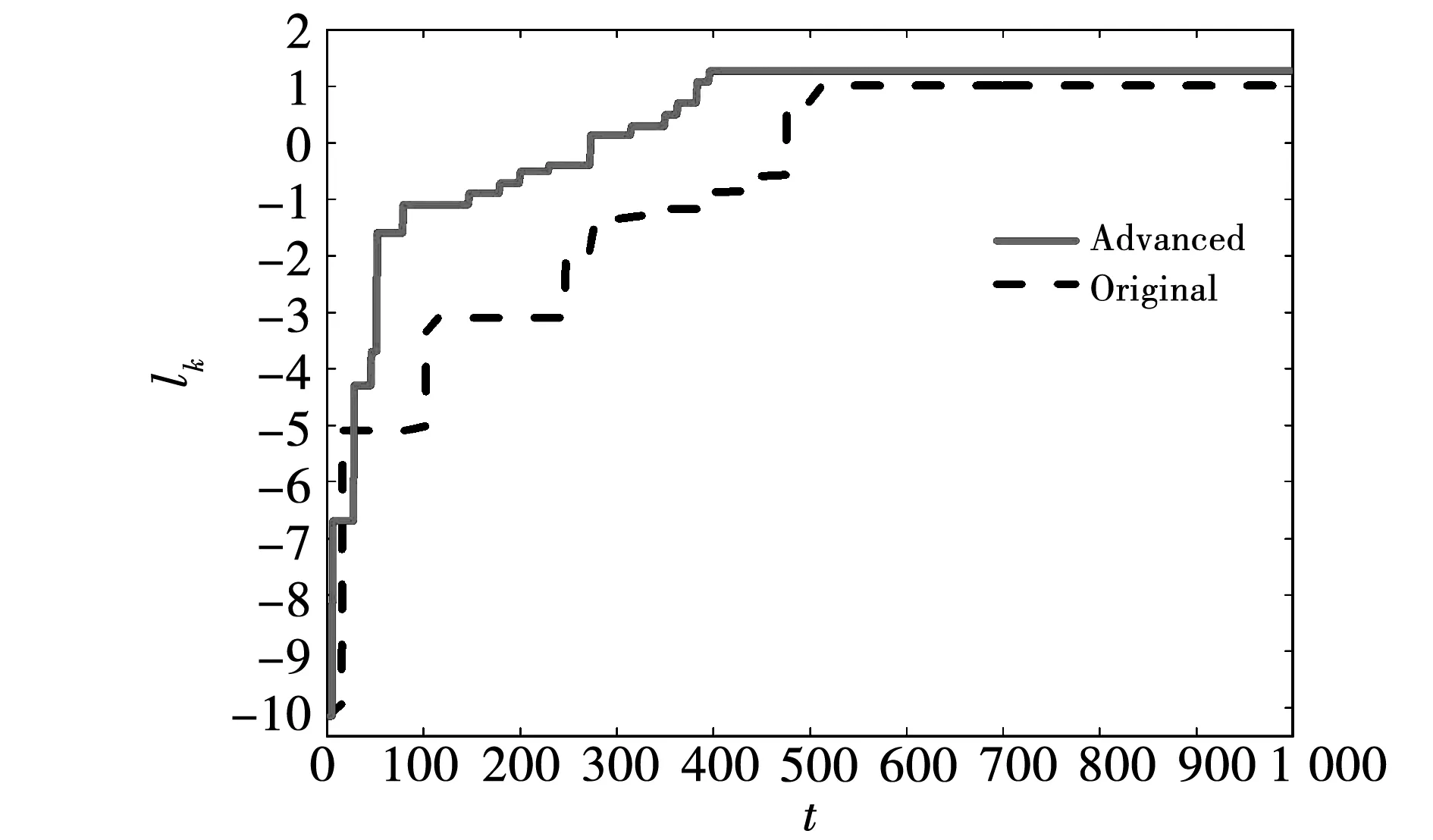
图10 算法改进前后收敛性对比

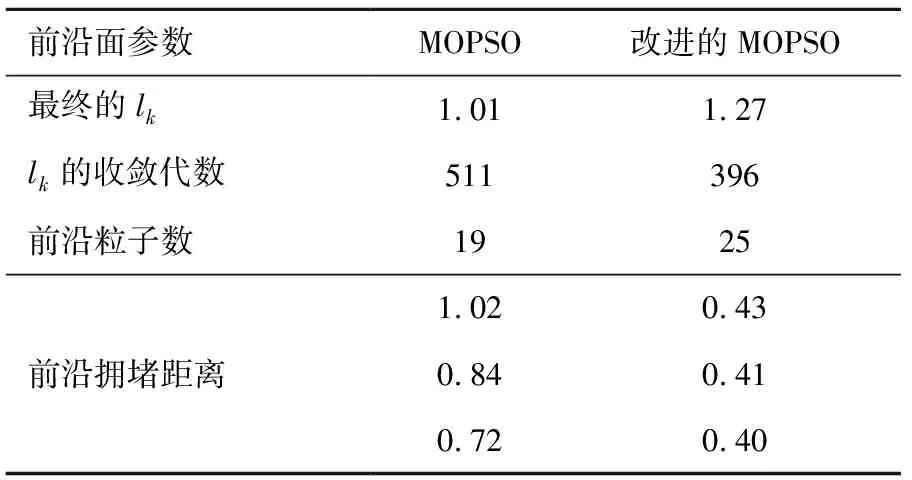
表1 算法改进前后性能对比

为了分析前沿面上不同尺寸永磁体的转矩性能，从改进后的算法优化结果上均匀选取5个点如图9，转矩分析如表2所示。永磁体尺寸由P1至P5顺序变化时，自旋转矩最大值增大，俯仰转矩最大值和平均值减小，自旋转矩平均值则出现了先增大后减小的变化。再结合数据变化差值，选取P2点作为电机永磁体尺寸优化的最优解，其尺寸参数如表3所示，示意图如图11所示。

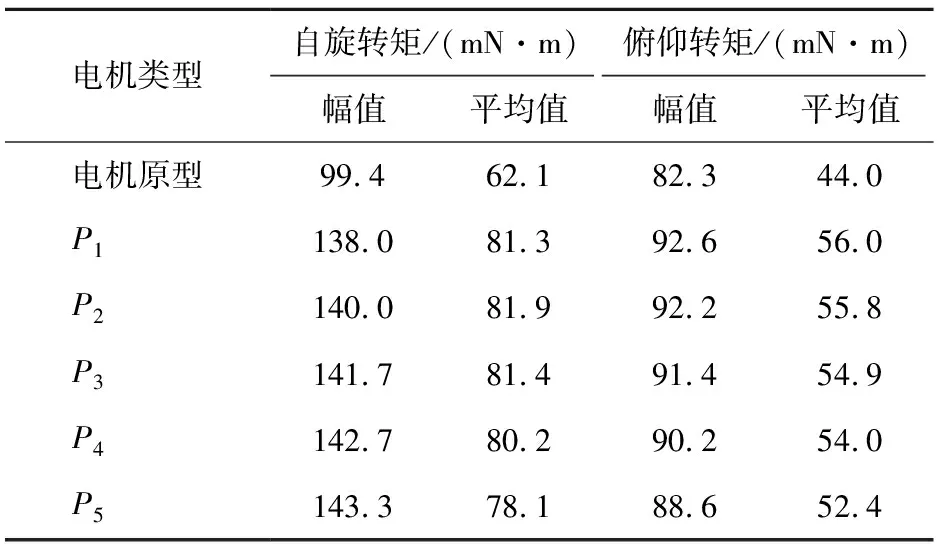
表2 转矩性能对比

表3 优化后的磁极尺寸

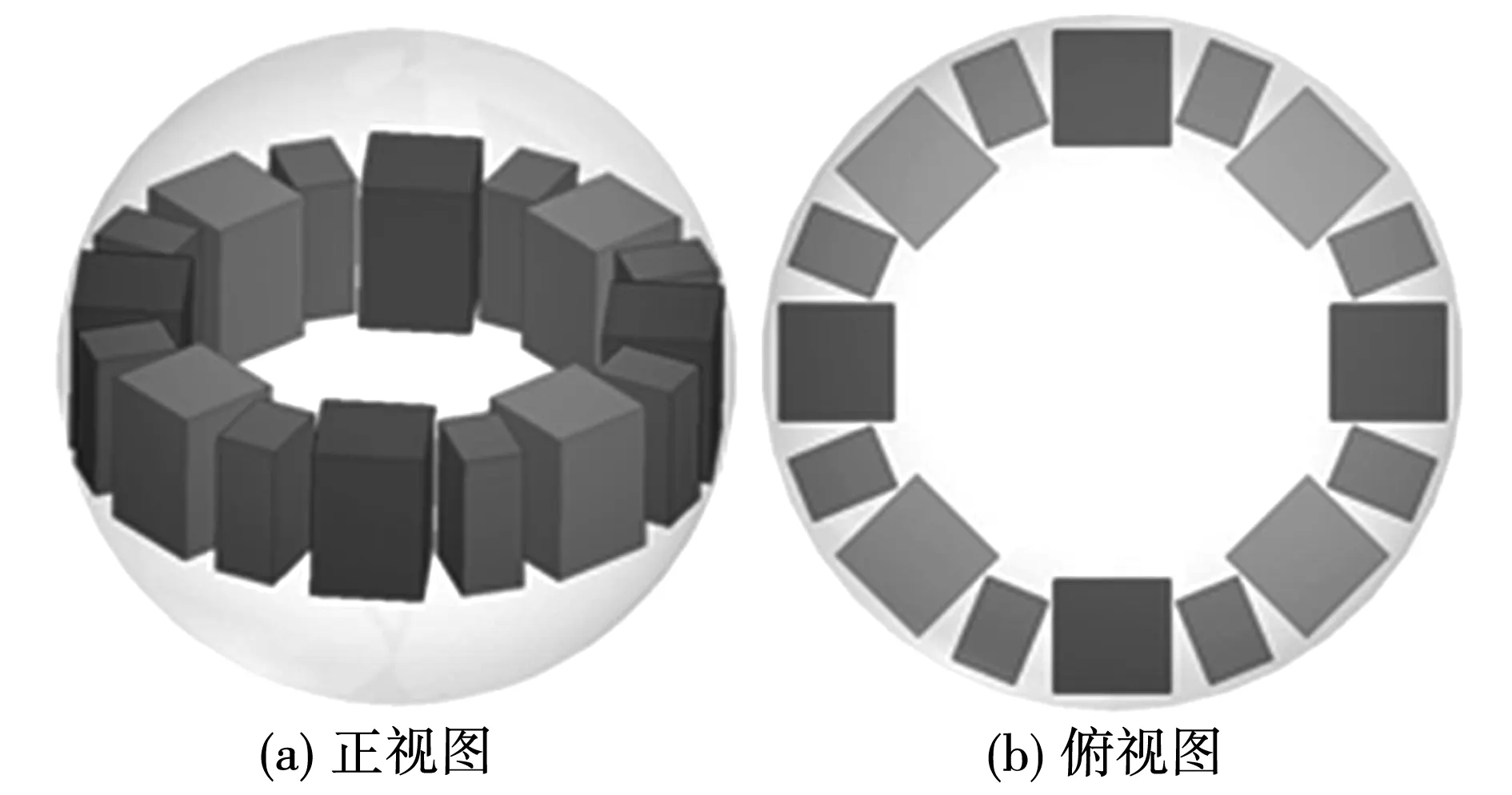
图11 优化后的电机磁极示意图

针对优化后的电机，给位于零经度的线圈施加1 A的电流，假设转子分别做如下运动：由-45°至45°绕z轴自旋运动，期间章动角和进动角保持为0；由-30°至30°绕y轴俯仰运动，期间自旋角和章动角保持为0。运动过程中的转矩解析计算值及Ansys仿真值如图12所示。优化后的自旋转矩幅值、平均值和俯仰转矩幅值、平均值分别提升了40.8%、31.9%、12.0%、26.8%。

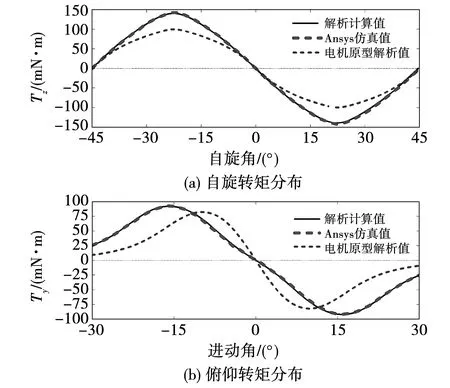
图12 优化后电机的转矩分布及对比

4 结 论

为了优化永磁球形电机的输出转矩整体性能，本文针对一种八极Halbach磁极阵列电机原型推导出应用洛伦兹力法的转矩解析模型，并进行了有限元仿真和实验对比验证。分析了磁极之间的约束关系，转子球尺寸不变，改变主磁极和过渡磁极的长、宽、高，以自旋转矩幅值和俯仰转矩幅值为目标进行了MOPSO优化。优化后的电机转矩性能较电机原型大幅提升，自旋幅值、平均值和俯仰转矩幅值、平均值分别提升了40.8%、31.9%、12.0%、26.8%。

在MOPSO的实现过程中，对Pareto前沿面上全局最优解的选取策略进行了两点改进，引入的凸点距离刺激能加速前沿面收敛，引入拥堵距离的补充寻优使得算法获得分布更加均匀的前沿。