一类耦合电感-二极管-电容组合的高增益DC-DC变换器
2022-07-15荣德生陈靓孙瑄瑨宁博
荣德生, 陈靓, 孙瑄瑨, 宁博
(1.辽宁工程技术大学 电气与控制工程学院,辽宁 葫芦岛 125105;2.国网辽宁省电力有限公司葫芦岛供电公司,辽宁 葫芦岛 125105)
0 引 言
随着光伏发电技术[1]不断推广和应用,其核心部件DC-DC变换器的高效高增益[2-4]的研究,逐渐成为光伏发电系统[5]研究的热点。
目前实现DC-DC变换器高增益的技术方向[6-9]多种多样。其中含耦合电感变换器[10-16]是升压变换器的一大典型类别,在提高了电压增益的同时实现了调节输出的灵活性和可控性,时下应用广泛。但该类变换器由于漏感的存在,实现高增益的同时,降低了变换器的工作效率;且传统的单一耦合结构会与寄生电容发生谐振,造成瞬间的尖峰电压,不但增加开关管电压应力,还会影响变换器乃至发电系统的整体稳定性。
围绕如何解决上述问题,学者们开展了一系列的研究:文献[10]在单一的耦合结构上提出双耦合设想,能够提高变换器增益,但无法改善原有的漏感问题;文献[11-12]不拘泥于传统结构,结合开关电容与耦合电感变换器,进一步提高电压增益,但不可避免地增加了磁件设计的难度;文献[13]基于传统耦合电感网络,并引入三电平思想,提高了电压增益,仍缺乏对开关管电压应力的有效降低手段;文献[14]针对耦合电感型Boost变换器引入钳位、整流单元等技术,初步解决了耦合电感的漏感问题,但缺少具体的实验应用分析;文献[15]在文献[14]的基础上进一步系统阐述耦合电感变换器的各类拓扑结构,剖析内在联系,其中重点对有源钳位的改进方式,采用能量吸收支路的思路;文献[16]对文献[15]中提出的耦合电感变换器详细解析,提出耦合电感倍压单元结构,引入一般变换器提高其增益,但仍做不到无损吸收漏感能量。
本文在文献[9]所提基本耦合电感Boost变换器的基础上,分析耦合电感类DC-DC变换器的构成。将耦合电感副边与一组二极管-电容(D-C)结构进行组合得到副边倍压结构,再将该结构与开关电容结构相结合,即可得到耦合电感-二极管-电容组合结构。在此基础上拓展出一类耦合电感-二极管-电容组合的高增益DC-DC变换器,这一类变换器在实现变换器高增益变换的同时,利用结构中一个D-C支路为钳位吸收支路,抑制由于漏感与开关器件寄生电容谐振所产生的电压冲击。以其中一种采用该单元结构的变换器为例,详细分析该结构变换器在CCM(continuous conduction mode,CCM)模式和DCM(discontinuous conduction mode,DCM)模式下变换器的工作原理,最终通过仿真与搭建实验机对理论进行验证。
1 变换器拓扑结构提出
1.1 耦合电感Boost变换器组成
文献[5]所提的基本耦合电感Boost变换器如图1所示,该变换器由三部分组成:带有耦合电感原边的前级储能结构、带有耦合电感副边的倍压结构以及二极管电容(DC)输出结构。
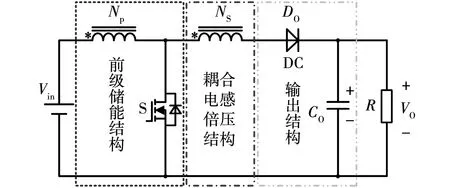
图1 基本耦合电感Boost变换器
对于具有耦合电感的升压DC-DC变换器来说,其均可由上述三种结构组合而来。其中,耦合电感倍压结构是实现变换器高增益变换的关键环节。
1.2 耦合电感-二极管-电容组合的高增益DC-DC变换器的构造思路
构建耦合电感-二极管-电容组合的高增益DC-DC变换器,从以下三部分进行分析:
1)前级储能结构。
对于耦合电感PWM型变换器来说,据耦合电感原边n1和开关管S位置的不同,可以简单地分为Boost型和Buck-Boost型两种结构,如图2所示。
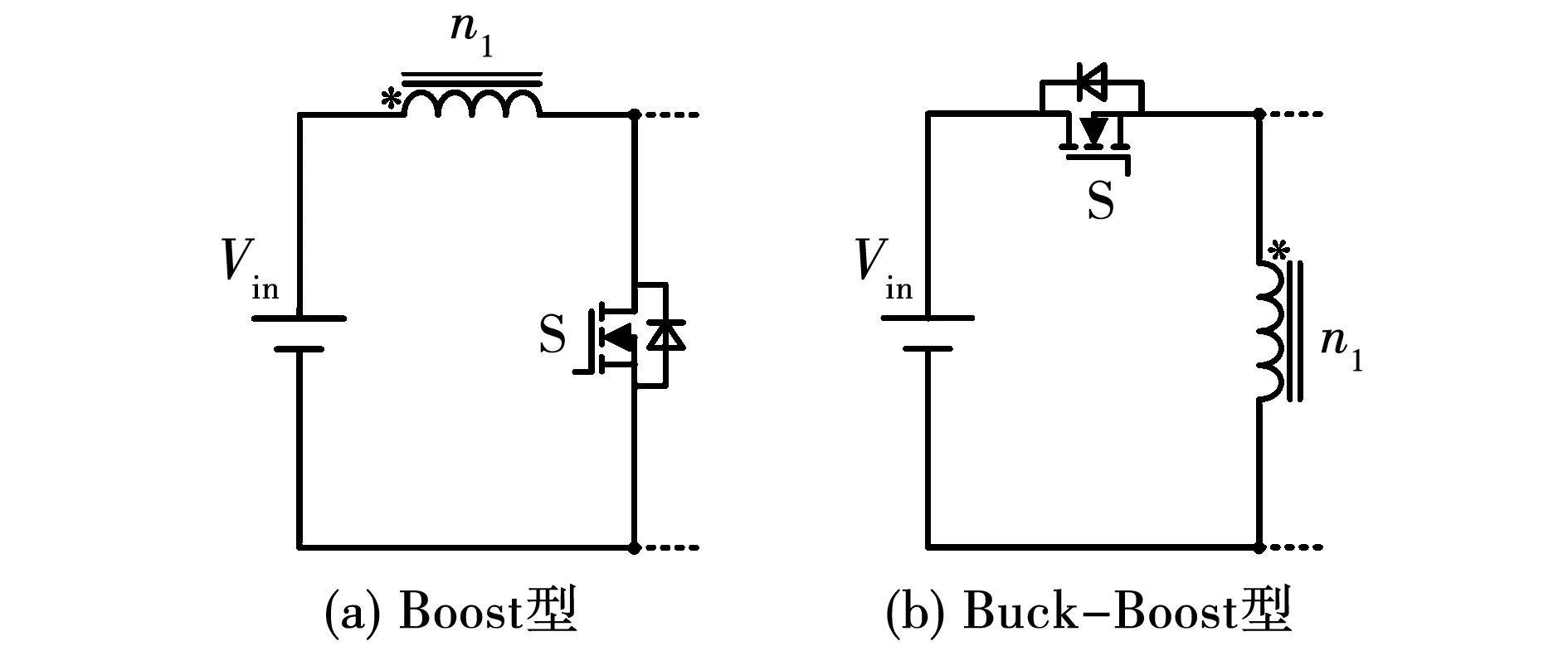
图2 两种前级结构
根据不同的前级结构,即可对后级耦合电感倍压结构进行设计。
2)耦合电感-二极管-电容组合结构。
由于耦合电感副边n2的能量是由原边n1储能得到的,故其可与一组二极管-电容(D-C)结构进行组合,得到副边组合结构如图3(a)所示。再将该结构与开关电容结构相结合,即可得到耦合电感-二极管-电容组合结构。该结构利用耦合电感漏感抑制了开关电容中较大电流冲击,同时还可以利用开关电容中结构中的一个的D-C支路作为耦合电感的钳位吸收支路,抑制了因漏感产生的开关管两端较大的电压冲击。
以一种常见的“X型”开关电容结构为例,依据上述思想,引入副边组合结构,得到一种耦合电感-二极管-电容组合结构如图3(b)所示。其中,二极管D2-C1为开关管的钳位支路。
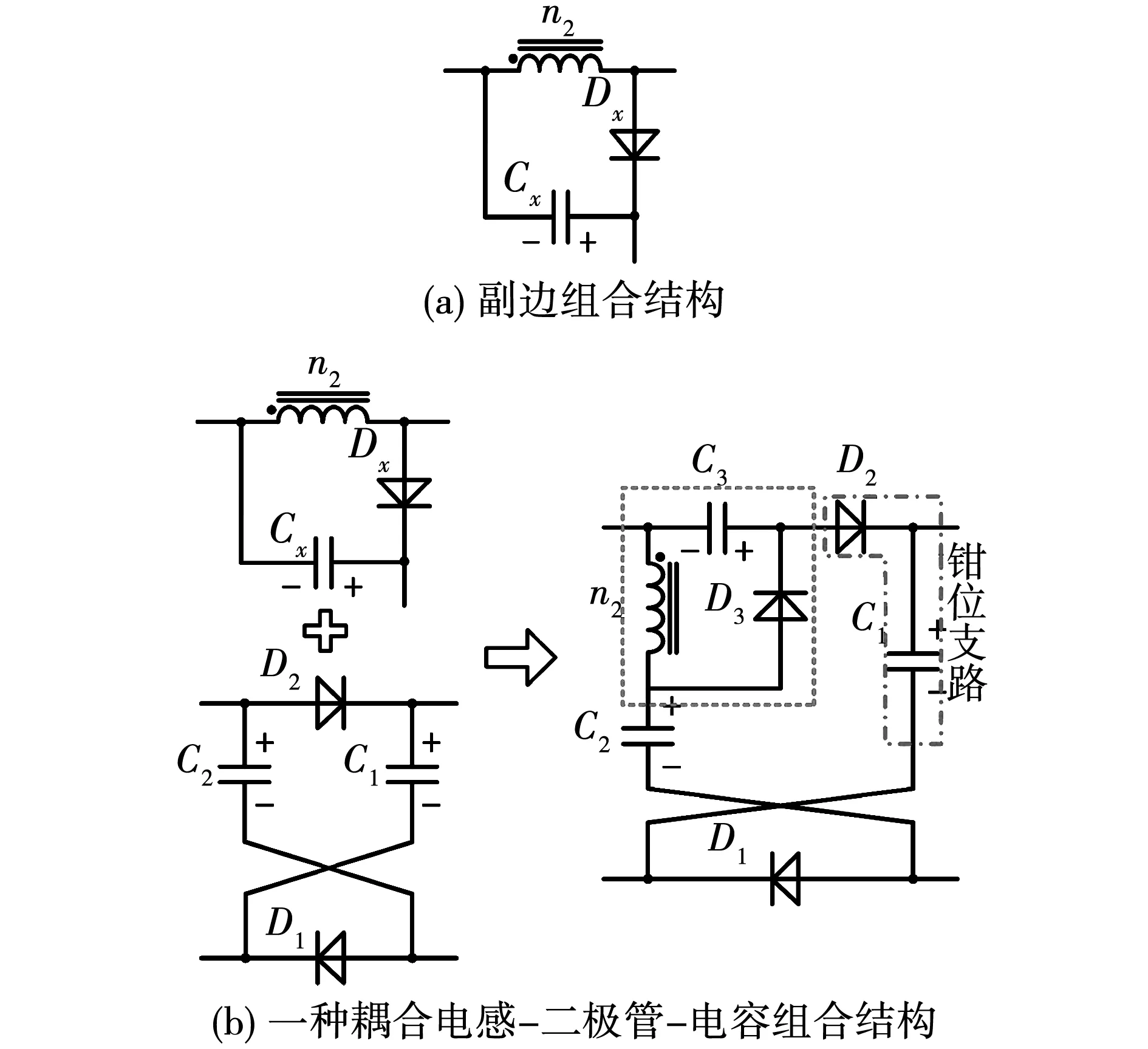
图3 耦合电感-二极管-电容组合结构构成
3)D-C输出结构。
变换器的输出D-C结构根据输出二极管方向,可分为同向输出型以及反向输型,两种结构如图4所示。
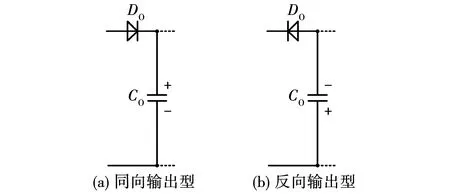
图4 两种输出结构
将上述三个部分选取合适结构进行级联,即可构造出高增益耦合电感-二极管-电容组合的耦合电感高增益变换器。
1.3 一类耦合电感-二极管-电容组合的高增益DC-DC变换器
依据1.2节的构造思路,可提出一系列的耦合电感-二极管-电容组合的耦合电感高增益变换器。根据不同的前级结构,可分为Boost型变换器族和Buck-Boost型变换器族,对应的两类拓扑结构如图5、图6所示。

图5 高增益耦合电感Boost变换器族
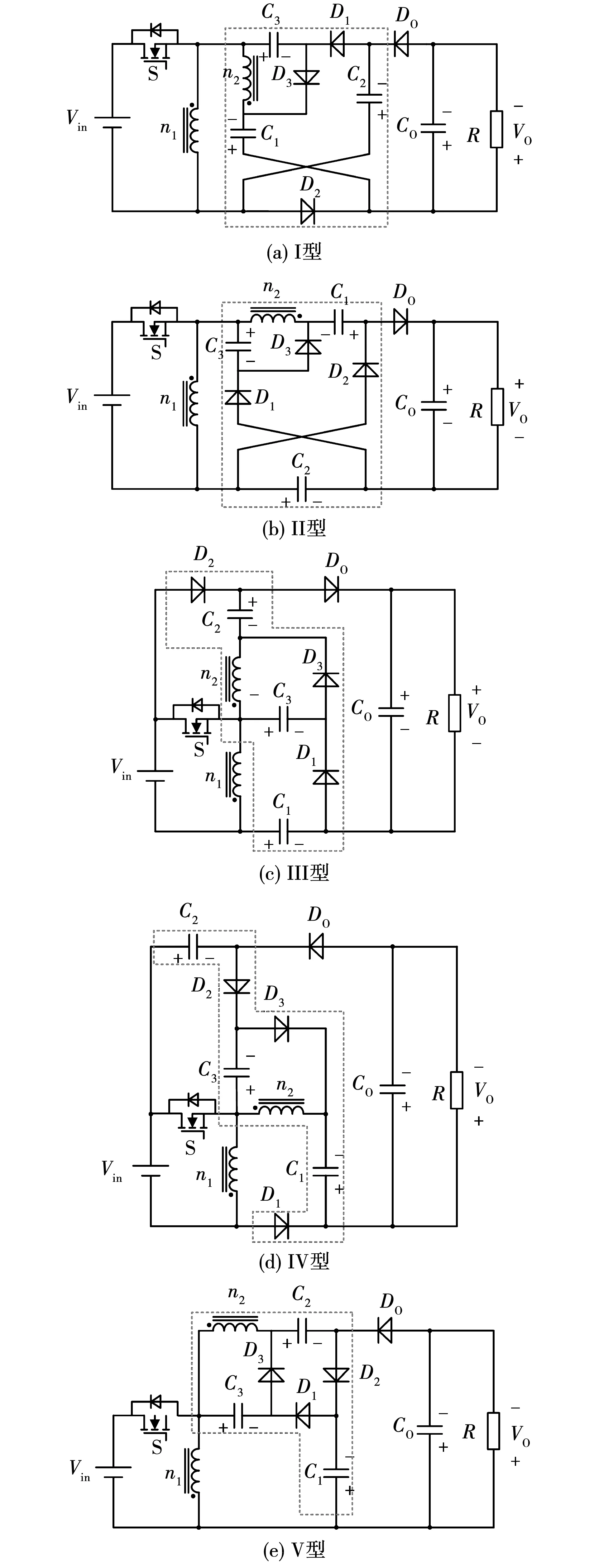
图6 高增益耦合电感Buck-Boost变换器族
2 变换器拓扑分析
选取图5(a)中的I型高增益耦合电感Boost变换器结构做具体的拓扑分析,其等效结构如图7所示。其中耦合电感结构由耦合电感漏感Lk,励磁电感Lm,以及匝比N=n2/n1的理想变压器组成。
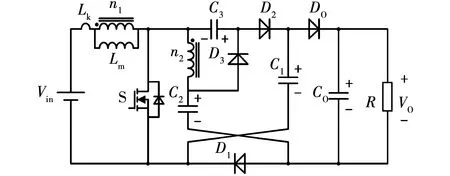
图7 变换器的等效电路图
2.1 工作原理
为便于变换器工作原理分析,有以下假设:
1)开关管、二极管为理想器件,导通关断时间为0、导通压降为0;
2)电容为理想器件,忽略电容的纹波电压;
3)考虑耦合电感漏感Lk对变换器性能的影响,耦合系数k=Lm/(Lm+Lk)、耦合电感匝比N=n2/n1。
2.1.1 CCM模式
当变换器一个开关周期内,励磁电感电流连续,即变换器工作在CCM模式下。此时共存在5种工作模态,其基本波形如图8所示,对应的工作模态如图9所示。
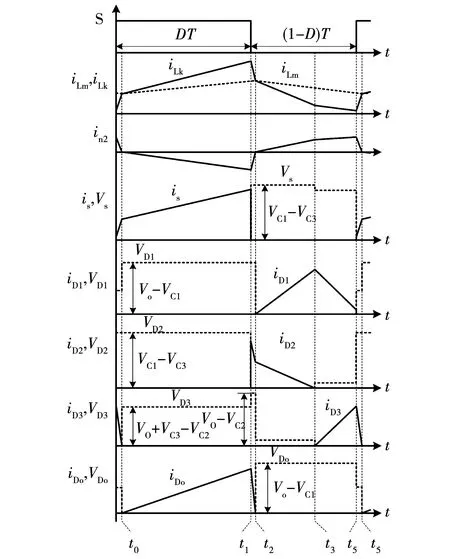
图8 CCM工作模态基本波形
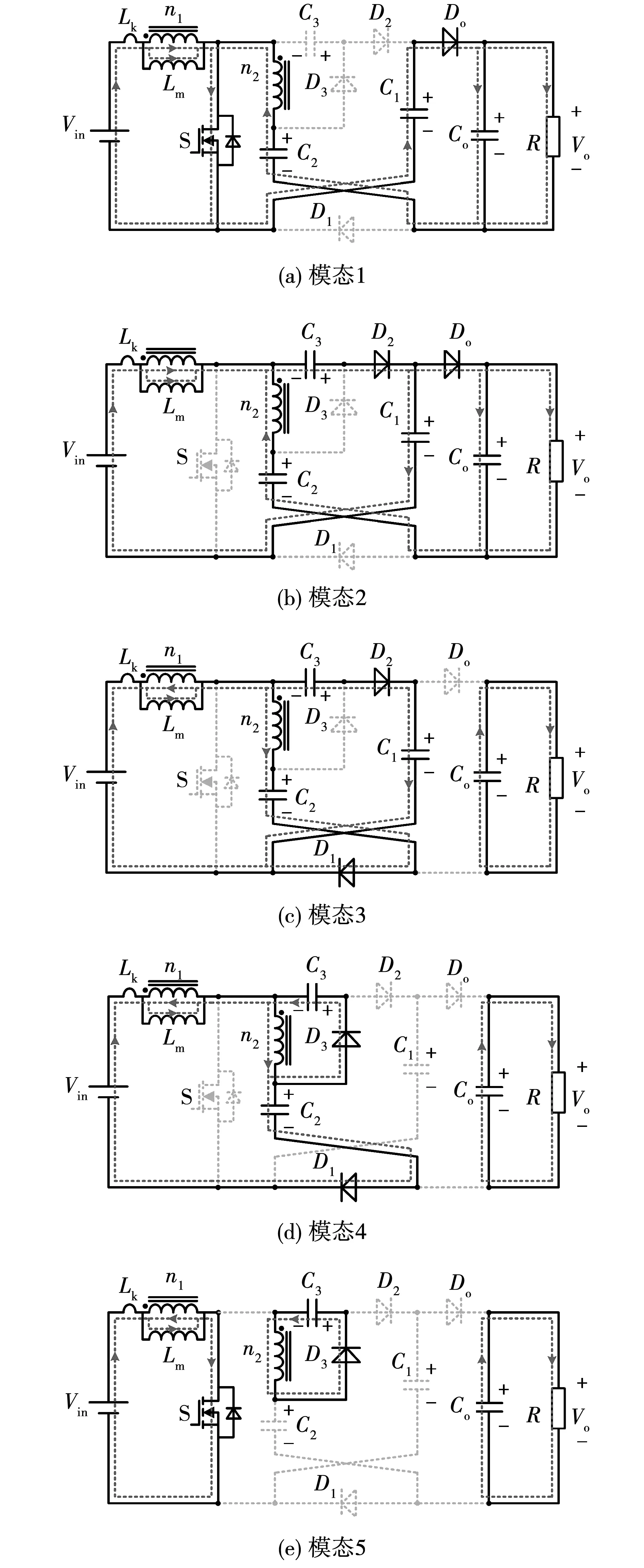
图9 变换器CCM工作模态
工作模态1[t0,t1]:开关管S开通,二极管D1,D2,D3截止,Do导通;电源通过S为电感Ln1储能,励磁电感电流iLm及漏感电流iLk增加;耦合电感的二次侧经C1,C2过S与D3为负载供电。
工作模态2[t1,t2]:由于较小的漏感该阶段时间短,S关断,二极管D2,Do导通,D1,D3截止;漏感Lk,C3放电给C1,其电流快速下降,将开关管S的端电压钳位于VC1-VC3;同时,输入电源同耦合电感二次侧过C2为负载供电。至t2时刻,电流iLn2下降为零,Do关断,模态结束。
工作模态3[t2,t3]:开关管仍关断,二极管D1,D2导通,D3,Do截止;漏感Lk与电容C3为C1充电,电流iLk与电流iD2持续下降;输入Vin串联耦合电感原副边通过D1共同为电容C2充电,电流iD1自零线性上升;电容Co为负载供电。至t3时刻,电流iLD2下降为零,D2关断,模态结束。
工作模态4[t3,t4]:,开关管S继续关断,二极管D1,Do截止,D2,D3导通;输入Vin串联耦合电感原副边仍为C2充电;耦合电感副边Ln2通过D3放电给电容C3;此时,电感L1经过D1为电容C3充电;电容Co持续为负载供电。
工作模态5[t4,t5]:此段极小时间内S导通,二极管D2,Do截止,D1,D3导通;输入电源Vin为电感Ln1储能,一次侧电流线性上升;耦合电感副边仍为电容C3放电;电容Co依旧提供负载供电。至t5时刻,二次侧电流下降为零,D3关断。
2.1.2 DCM模式
当变换器一个开关周期内,励磁电感电流断续,即变换器工作在DCM模式下。此时共存6种工作模态,对应工作模态如下图10所示,其基本波形如图11所示。
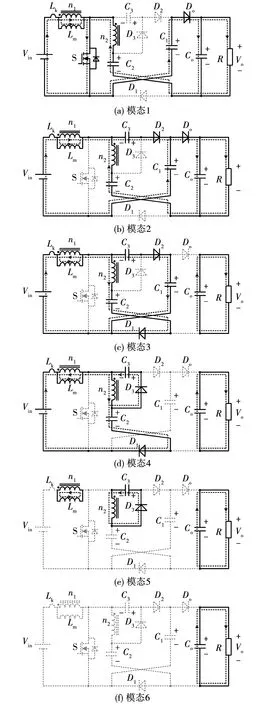
图10 变换器DCM工作模态
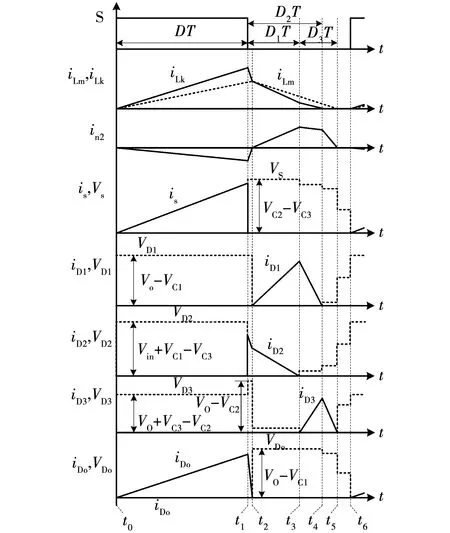
图11 DCM工作模态基本波形
其中,工作模态2[t1,t2]与工作模态3[t2,t3]同CCM模式下的一致,不再具体赘述。
工作模态1[t0,t1]:开关管S开通,二极管D1,D2,D3截止,Do导通;电源通过S电感为Ln1储能,励磁电感电流iLm及漏感电流iLk增加;耦合电感的二次侧经C1,C2过S与D3为负载供电,电流iDo自零线性上升。
工作模态4[t3,t4]:开关管S继续关断,二极管Do,D2截止,D1,D3导通;输入Vin串联耦合电感原副边过二极管D1为C2充电,iD1线性下降;耦合电感副边Ln2通过D3放电给电容C3;电容Co持续为负载供电。至t4时刻,电流iD1下降为零,D1关断,模态结束。
工作模态5[t4,t5]:开关管S继续关断,二极管D1,D2,Do截止,D3导通;耦合电感副边Ln2通过D3放电给电容C3,电流iD3线性下降;电容Co依旧提供负载供电。至t5时刻,电流iD3下降为零,模态结束。
工作模态6[t5,t6]:开关器件均关断,此时电感电流断续模态,励磁电感Lm、漏感Lk不再释放能量,电容Co依旧提供负载供电。
2.2 变换器稳态分析
1)性能分析。
经上节对变换器在CCM模型下的模态分析,对稳态分析时可忽略时间较小的过渡模态,即不考虑模态2和模态5。
工作模态1各回路电压关系为:
(1)
工作模态3各回路电压方程为:
(2)
对应工作模态4存在如下电压关系:
(3)
基于上述电压关系,根据电感电压伏秒积面积平衡原理可得变换器的电压增益
(4)
设k=1,各电容、二极管器件电压应力如下:
(5)
(6)
(7)
(8)
(9)
(10)
开关管S的电压应力为
(11)
2)临界电感值的计算。
在DCM模式下,忽略漏感对变换器影响的短时间模态,变换器的主要电流波形如下图12所示。此外,令占空比DL=D2+D3,为励磁电感Lm下降至零的占空比。
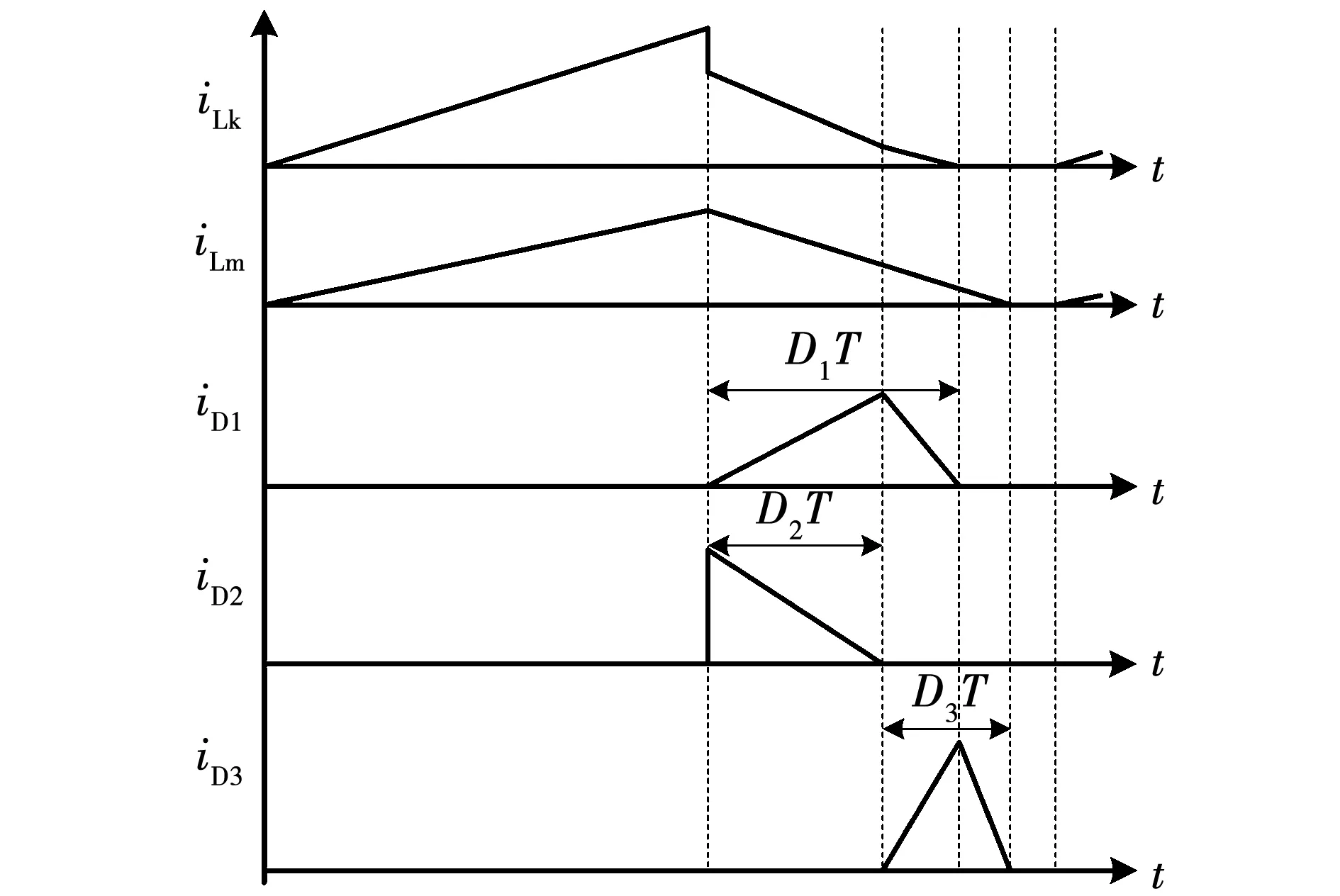
图12 DCM工作模态基本波形
设励磁电感电流iLm的峰值为
(12)
得到各二极管的平均电流如下:
(13)
(14)
(15)
k=1时,根据电容的安秒平衡原理,各二极管的平均电流等于输出电流Io,得电压增益为
(16)
引入励磁电感时间常数,表示为
(17)
得占空比DL的表达式
(18)
将式(18)回代式(16),得变换器C-DCM模式的电压增益
(19)
当变换器处于BCM模式,可推临界励磁电感时间常数为
(20)
根据时间常数表达式,对应临界励磁电感τLmB与占空比D的关系曲线如图13所示。当τLm>τLmB时,变换器工作在C-CCM模式,反之,变换器则处于C-DCM模式。
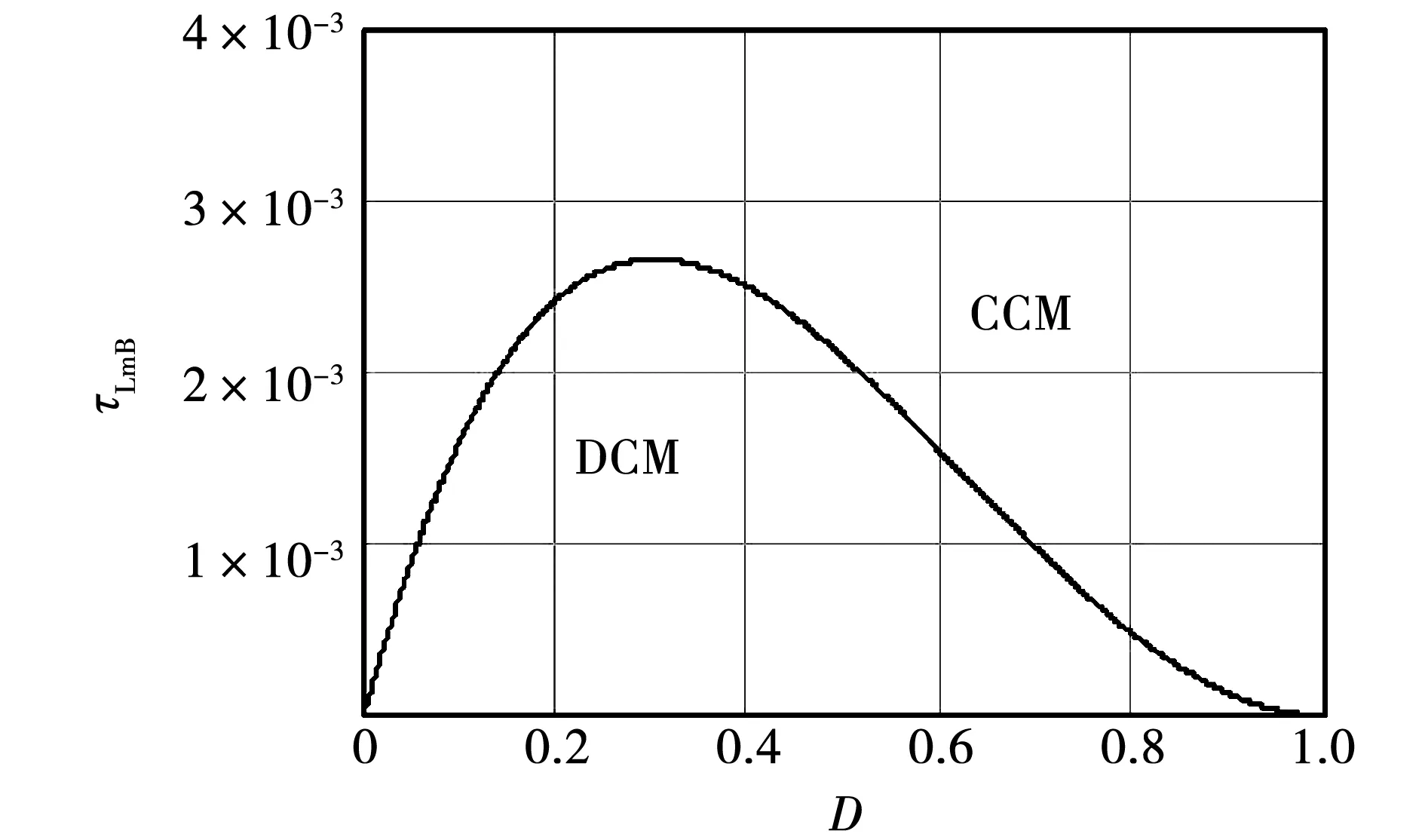
图13 临界励磁电感时间常数τLmB与占空比D(N=2)
3 变换器性能对比
将图5中本文提出的 I型变换器与常见的几类变换器对比,几种变换器的性能参数如表1所示。
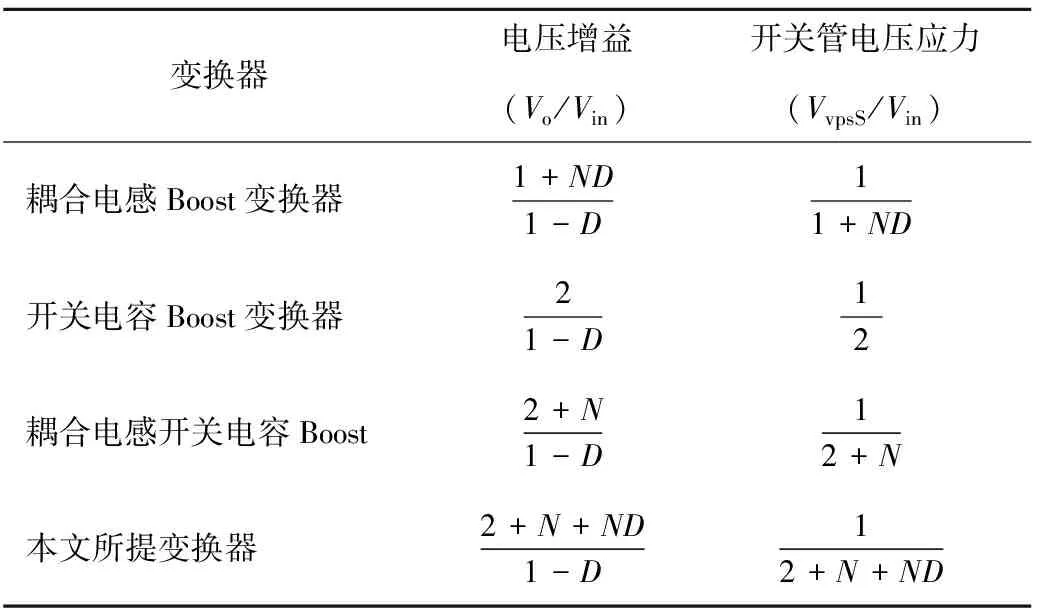
表1 变换器参数对比
以耦合电感的匝比N=2的固定情况为参考,上述四种变换器的增益对比曲线如图14,变换器的开关管电压应力对比曲线如图15。
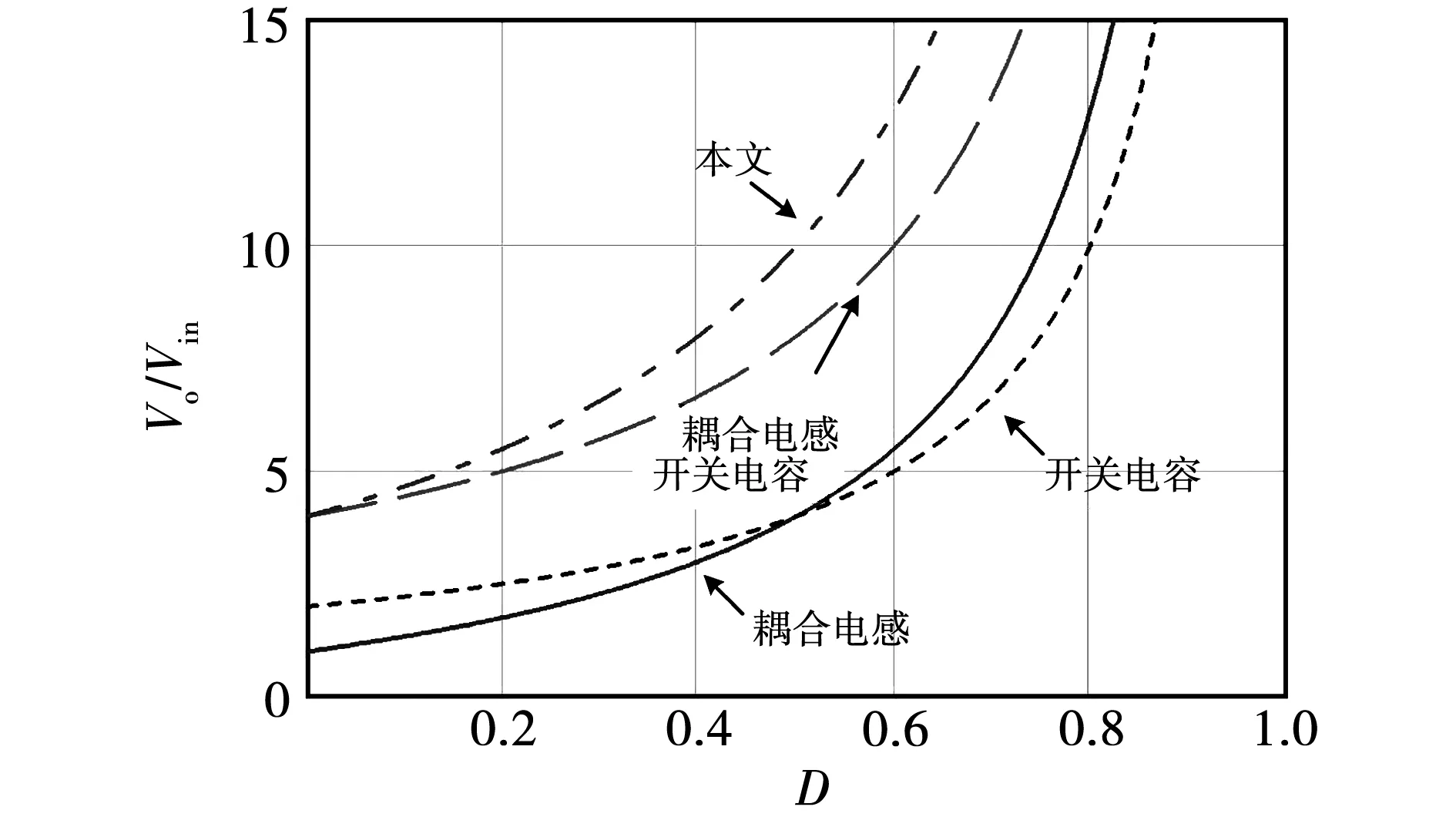
图14 变换器增益对比图
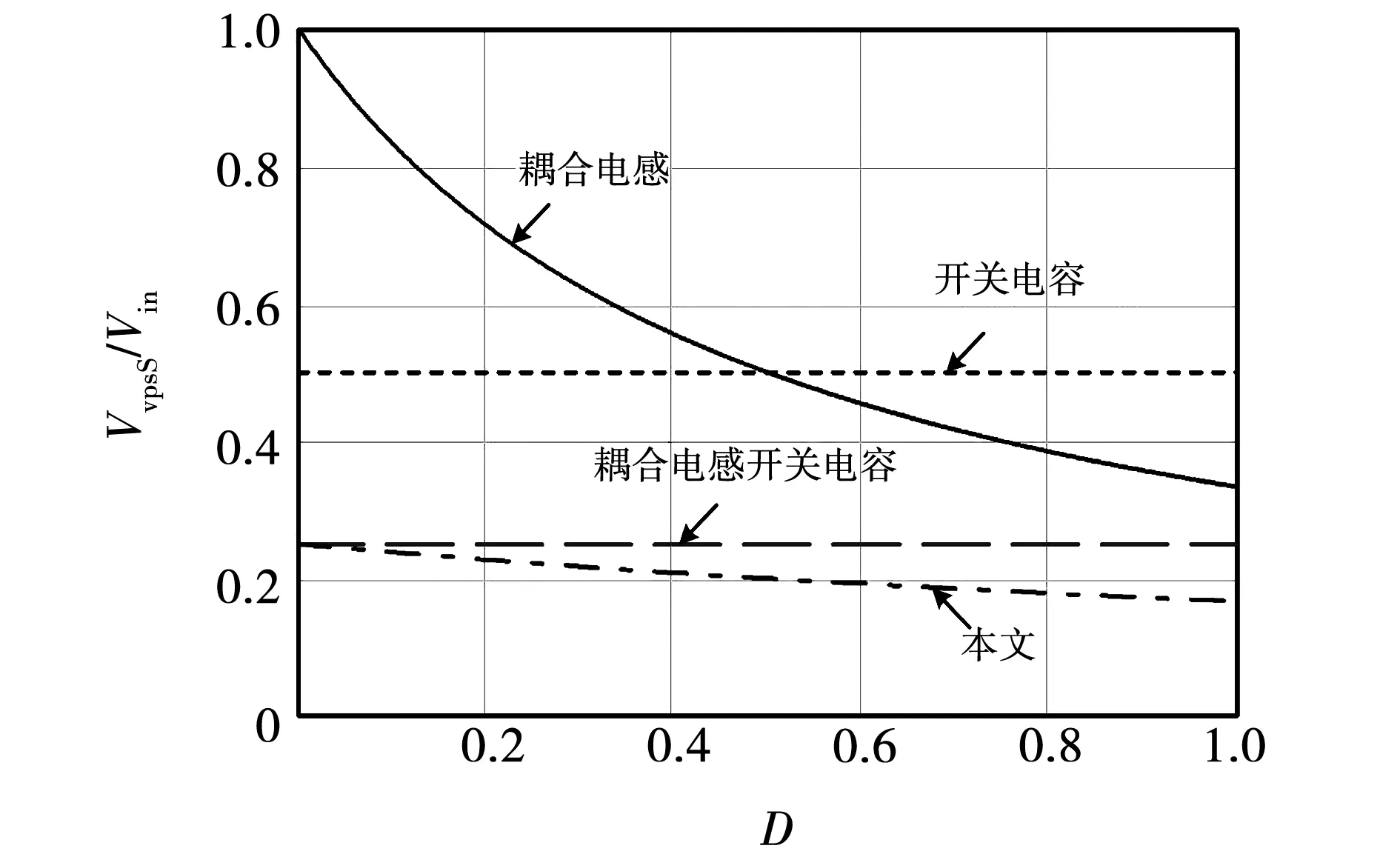
图15 开关管S电压应力对比图
由图14可知,本文所提高增益Boost型变换器性能在现有几大类变换器的基础上明显提升电压增益。而由图15可知,单元化改善的耦合电感变换器的电压应力最小,实际应用时能够选取电压应力更低的MOSFET器件。
4 仿真与实验
对于耦合电感高增益型DC-DC变换器来说,在CCM模式下变换器具有较小的电流纹波,对输出电容要求相对较低,有利于降低电容的容量与体积。故在进行仿真与实验中,采用CCM工作模式。
4.1 仿真验证
为初步验证上节理论分析,利用PSIM仿真软件,对图5中本文提出的I型变换器进行仿真实验。变换器的控制环路采用C Block模块实现,设置变换器参数如下:输入电压Vin=20 V,输出电压Vo=200 V,功率为150 W,耦合电感匝比n=2,开关频率f=50 kHz,电容C1=C2=C3=Co=100 μH,励磁电感Lm=60 μH,漏感Lk=1.8 μH。
变换器的电压仿真波形如图16所示,可以看出,在输出电压为200 V的情况下,开关管S的电压应力仅约43.7 V,变换器占空比D约为0.51,在高增益的情况下保持较低的电压应力,各个二极管电压应力也均小于输出电压。
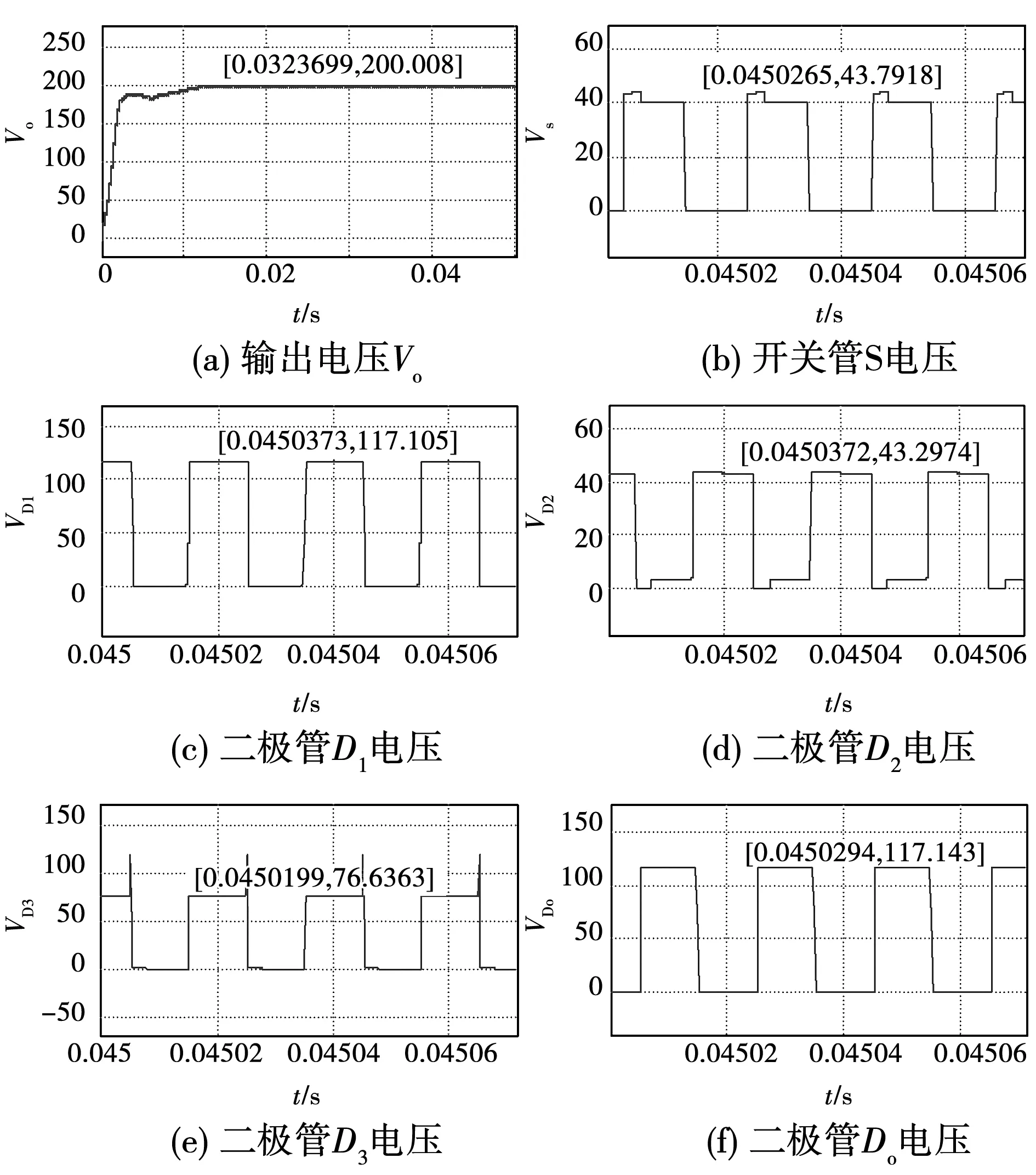
图16 变换器电压仿真波形
变换器电流仿真波形如图17所示。可以看出,耦合电感原、副边电流波形变化趋势与理论分析相符。二极管D2实现了零电流关断,二极管D1、D3、Do实现了零电流导通。
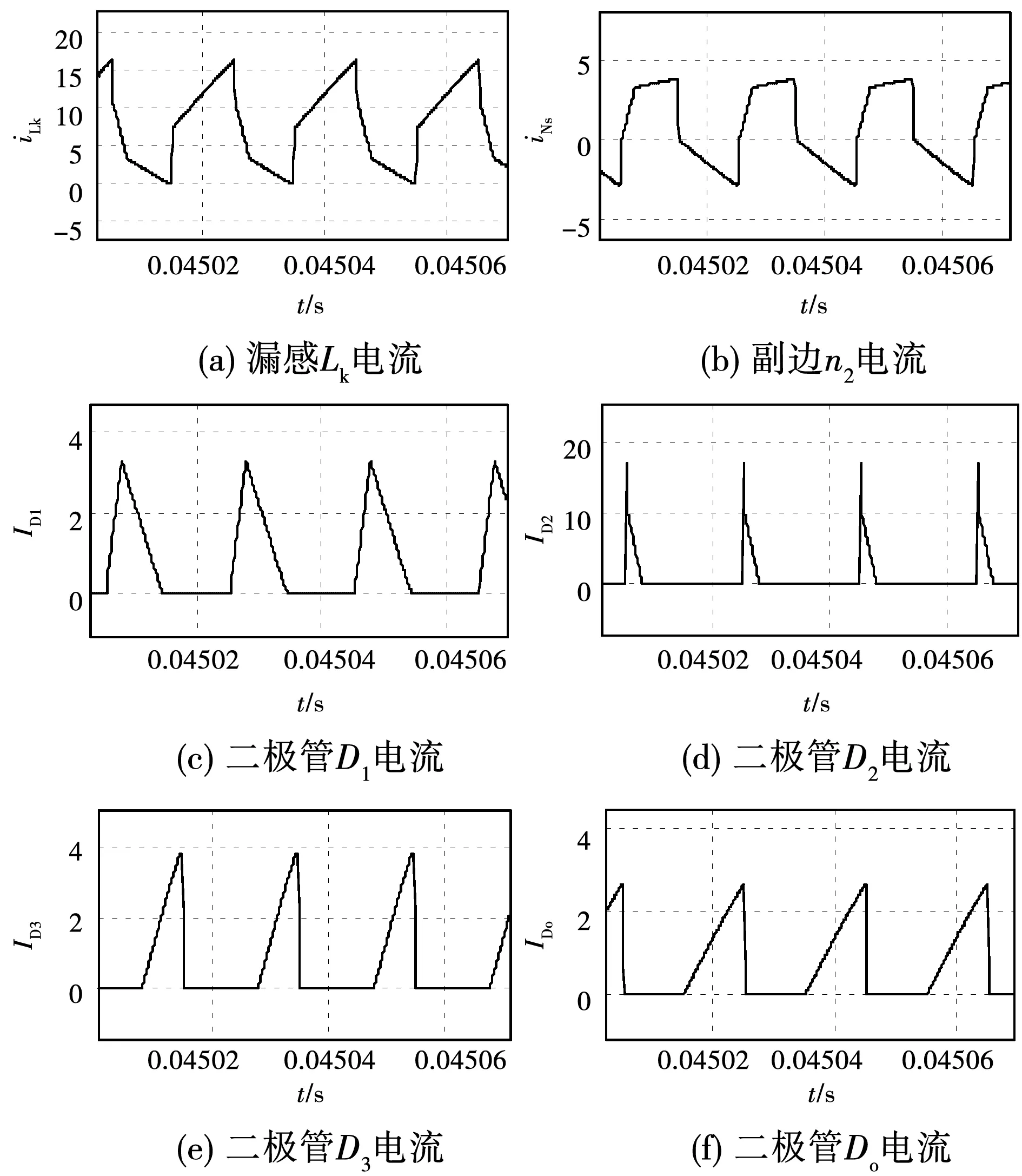
图17 变换器电流仿真波形
4.2 实验验证
对提出的高增益变换器设计理论进行实验验证,搭建一个150 W的样机,如图18所示。详细的参数见下表2。
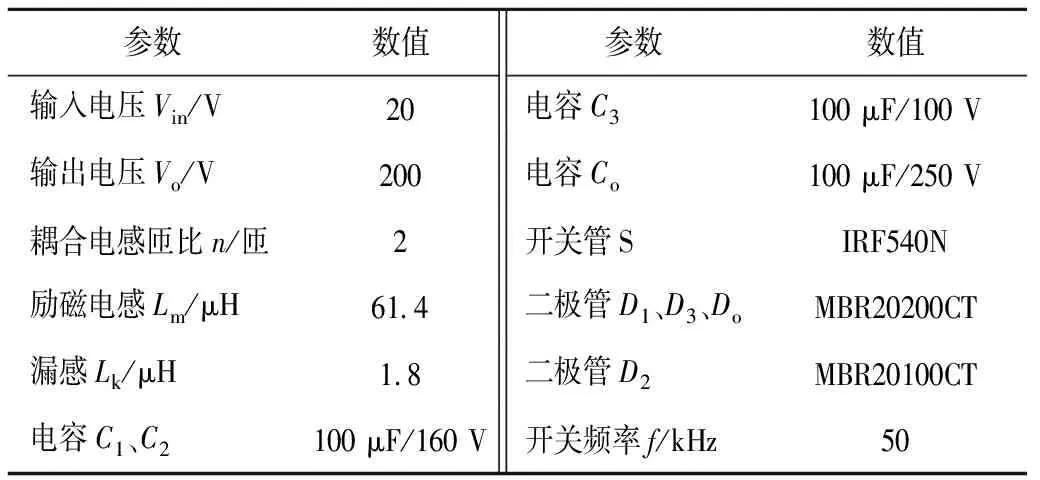
表2 实验样机参数

图18 实验样机平台
如图19所示,为变换器输出电压与开关管应力,其中变换器的输出电压约200 V,满足理论分析的高增益;同时,开关管S的电压应力仅约为43 V,实现了较低低电压应力,与仿真一致。
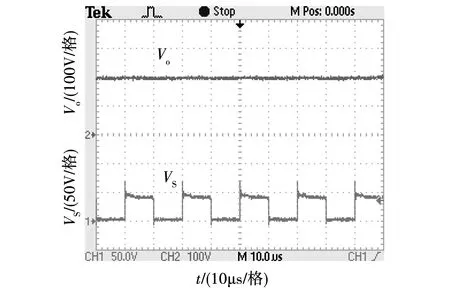
图19 变换器输出电压与开关管电压应力波形图
各开关器件的电压应力如图20中波形所示。由上下图知,二极管D2的电压应力约为43 V与开关管S相同;另外,D1、Do的电压应力相同,约为117 V;二极管D3为76 V。图中波形均符合理论分析,在电压应力参数上各个器件均具有良好表现。
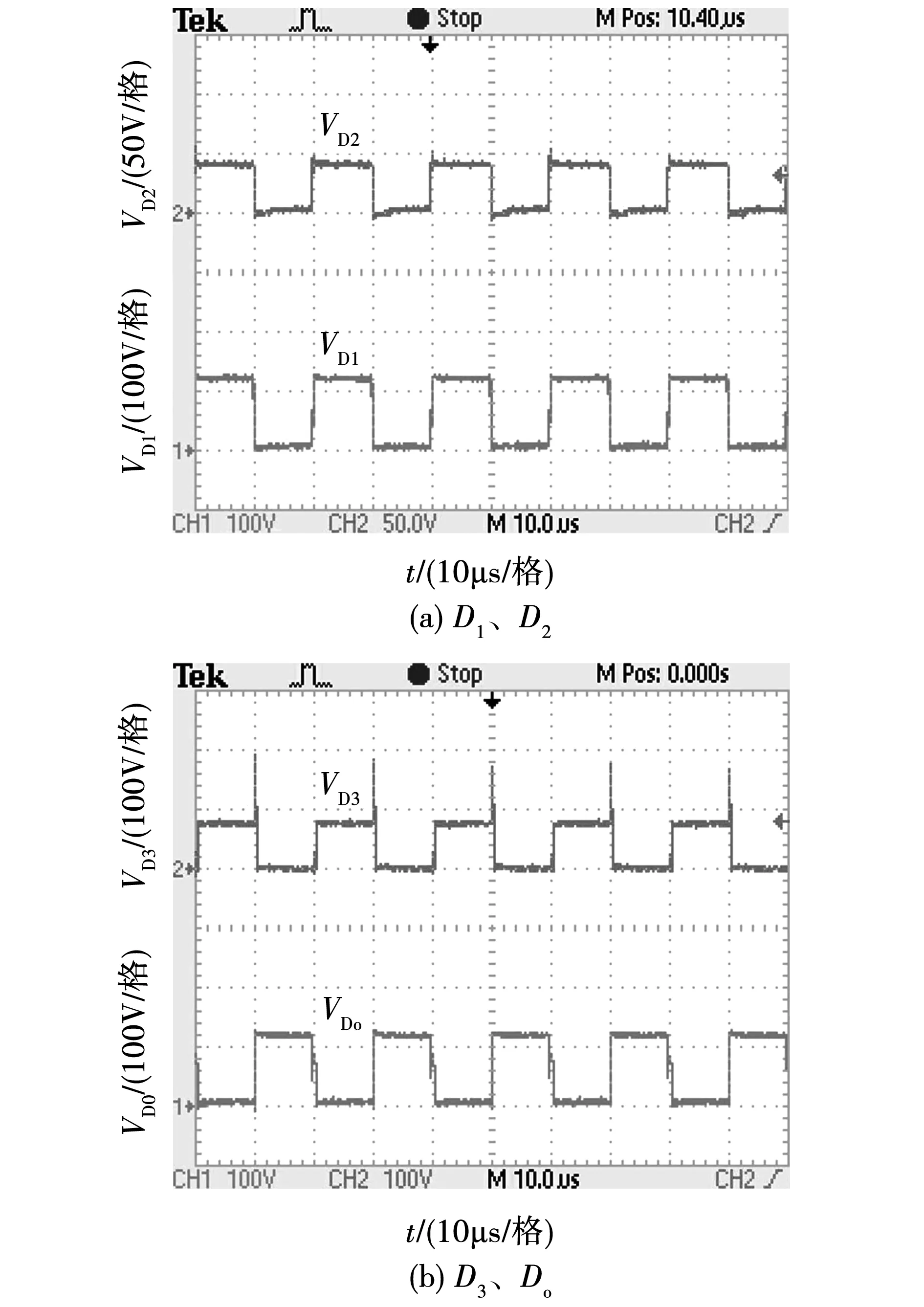
图20 变换器功率器件电压应力波形图
此外,变换器的各器件电流波形如图21,其中图21(a)为变换器一次侧漏感和副边电流波形图,图21(b)~图21(c)为二极管电流波形图。可以看出,二极管D2实现了零电流关断,二极管D1,D3,Do实现了零电流导通,实验结果与仿真一致。
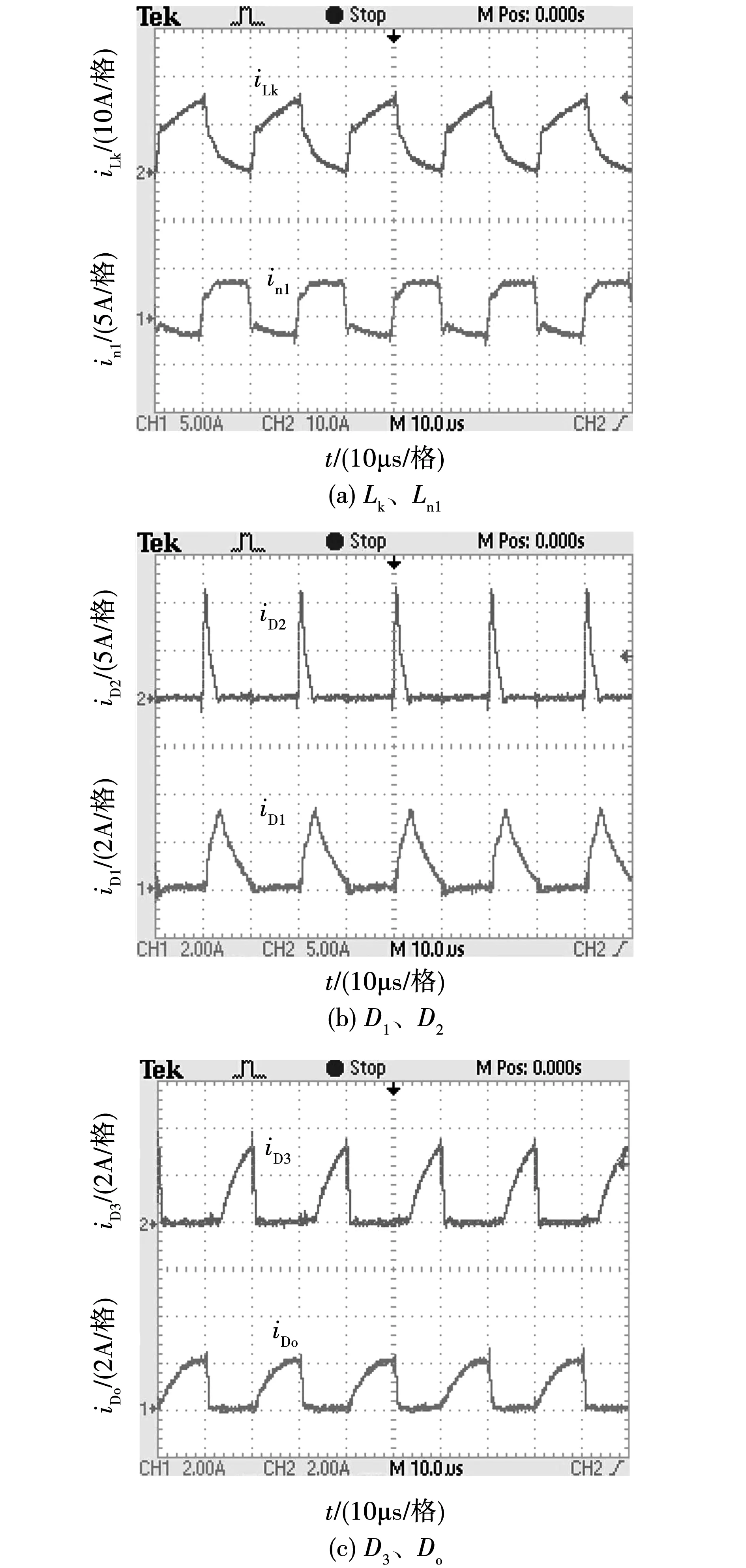
图21 变换器电流波形图
图22所示为本文所提变换器与表1中的几类常见升压变换器在20 V输入200 V输出情况下的参考效率曲线。可以看出本文所提变换器在由于具有较高的电压增益且共用漏感吸收回路,变换器整体效率较高,在110 W左右达到最高效率约为93.7%。由于变换器均采用手工制板,变换器效率还可进一步优化。
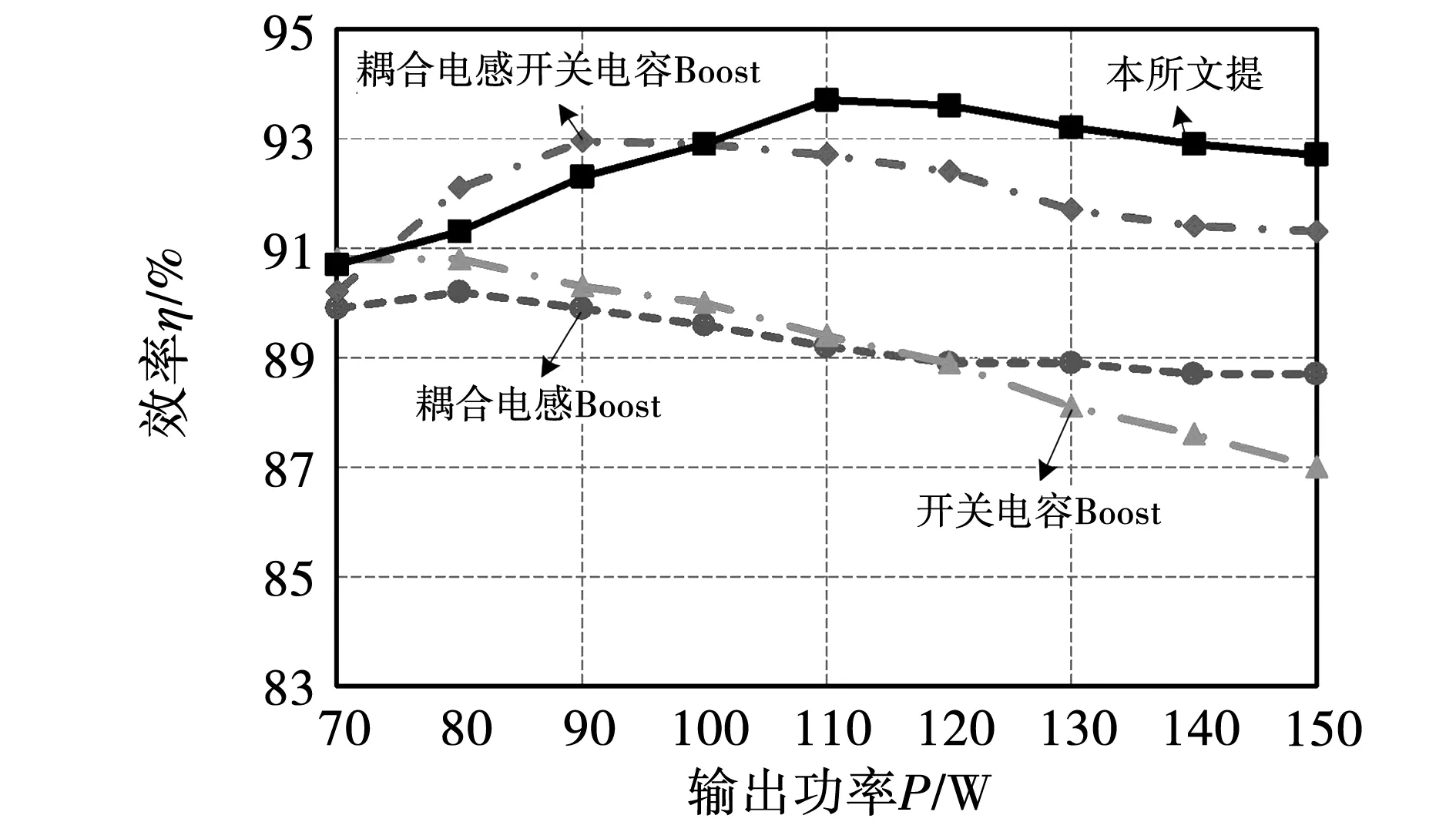
图22 变换器效率曲线对比
5 结 论
本文对基本耦合电感Boost变换器进行改造,通过添加多个辅助D-C支路,进一步推演出一系列耦合电感-二极管-电容组合的高增益DC-DC变换器,该变换器具有以下特点:
1)通过组合D-C支路,变换器的电压增益明显提升且增益可通过耦合电感匝比n灵活调节;
2)利用其中一个D-C为无源钳位支路,吸收漏感能量并在主开关管关断后,对其电压进行钳位,开关管具有较低的电压应力;
3)拓展出两类耦合电感-二极管-电容组合的高增益DC-DC变换器,分别为Boost型族和Buck-Boost型族,可应用于各种高效高增益场合。
