基于蝗虫优化Bi-LSTM网络的电机轴承故障预测
2022-07-15于飞樊清川宣敏
于飞, 樊清川, 宣敏
(海军工程大学 电气工程学院,湖北 武汉 430033)
0 引 言
滚动轴承的运行状态能够直接影响电机的整体性能,电机故障中有40%左右是由轴承故障引发[1],是电机健康监测的重要对象,通过有效评估电机轴承的退化状态并及时预测轴承故障,进行早期维护和检修,可以避免工业中的经济损失和重大安全事故。电机轴承故障预测的关键在于两点:一是确定合适的轴承性能退化指标,二是搭建有效的故障预测模型。
性能退化指标是故障判别标准的关键,现有的研究中大多用峰度、均方根、峰峰值等无量纲参数作为性能退化指标,预测模型是故障预测的核心,近年来有许多学者利用机器学习算法有效地实现了轴承的故障预测。文献[2]利用字典学习法对振动信号进行降噪处理,并采用反向传播(back propagation,BP)神经网络进行轴承故障预测,证明了BP神经网络在轴承故障预测中的有效性,但其权值和阈值的设置较大地影响了预测的精度;文献[3]使用递归能量化分析以及自回归模型实现了退化的检测和状态的预测;文献[4]引入了两种新型混合模型相互结合,实现了轴承的剩余寿命预测;文献[5]提出利用堆叠去噪自编码累积和时滞最小二乘支持向量机的牵引电机状态预测方法,利用堆叠去噪自编码器进行特征降维并获得相关退化指标,通过对退化指标的预测实现运行状态预测;文献[6]利用核主元分析法构建T2和SPE统计量作为电机轴承退化指标,将预处理过的振动信号输入支持向量机进行回归计算,实现了轴承性能退化趋势的合理追踪。循环神经网络(recurrent neural network, RNN)早已应用在轴承的健康状态预测中[7]。基于前人的研究,本文利用RNN的一个优秀变体——长短时记忆网络(long short-term memory, LSTM),LSTM具有良好的记忆存储特性,记录序列有用信息从而获得更优的预测精度。文献[8]将“波形熵”作为性能退化指标,利用LSTM网络实现了滚动轴承的寿命预测。上述方法都实现了轴承退化状态的有效预测,但在方法的精度和稳定性上有待提高。
高质量的数据特征能够大大提高预测分析的性能,集合经验模态分解(ensemble empirical mode decomposition, EEMD)作为一种自主分解数据方法解决了经验模态分解存在的模态混叠等现象,在处理振动信号时效果较好,但其分解后遗留在分量中的白噪声会出现重构误差,为解决以上问题,本文选择利用互补经验模态分解[9]提取振动信号的固有模态分量(intrinsic mode function,IMF),并计算各组IMF分量的奇异值能量谱确定性能退化指标,再提出使用蝗虫优化算法优化双向长短时记忆网络(bidirectional long short-term memory,Bi-LSTM)的故障预测模型。将该模型应用在电机轴承故障预测中,最后,实验对比分析证实了本文所提方法在电机轴承故障预测中的优越性。
1 性能退化指标构建
1.1 互补集合经验模态分解
模态分解的方法很多,互补集合经验模态分解(complementary ensemble empirical mode decomposition,CEEMD)是基于经验模态分解(empirical mode decomposition,EMD)和EEMD分解改进而来,既消除了EMD分解中时常存在的模态混叠现象,又优化了EEMD分解过程效率较低、时间过长的情况。CEEMD分解在信号中引入互补的高斯白噪声,借助噪声信号相互独立,绝对负相关,信号分解时能够尽可能地抵消掉冗余的噪声[10]。CEEMD分解过程如下:
1)在预处理的信号x(t)中加入N次幅值相同的互补白噪声μ,组成新的序列为:
(1)

(2)
式中cj为CEEMD分解的第j个IMF分量。
1.2 奇异值能量谱
当电机轴承将要出现故障时,各IMF的能量都会发生变化,信号能量逐渐分散,奇异值能量随之变化。当出现明显故障状态时,噪声比例快速增加,信号能量迅速增大,奇异值能量迅速增大。鉴于上述分析,奇异值能量谱可以作为表征电机轴承状态退化的性能指标。
振动信号经过CEMMD分解,得到IMF分量矩阵为
B=[IMF1,IMF2,…,IMFk]T。
(3)
对每组IMF分量进行奇异值分解(singular value decomposition,SVD),该项技术以其出色的去噪和周期成分提取效果,在故障诊断领域早有研究,奇异值分解的具体过程如下:
一个实矩阵A∈Rm×n,一定存在一个正交矩阵U=[u1,u2,…,um]∈Rm×n和正交矩阵V=[v1,v2,…,vn]∈Rm×n,使得
A=USVT。
(4)
式中S=[diag(s1,s2,…,sk),O],或其转置,O表示零矩阵,k=min(m,n),且有s1≥s2,…,≥sk>0,即为A的奇异值[12]。
解出矩阵B对应的奇异值矩阵为
S=[s1,s2,…,sk]T。
(5)
由文献[13]可知,信号能量可表示为
(6)
2 优化的Bi-LSTM模型
2.1 蝗虫优化算法
蝗虫优化算法(grasshopper optimization algorithm,GOA)是2017年由Arora[14]等人提出的一种新的启发式优化算法。算法思想是基于蝗虫觅食得来,每个蝗虫个体即为搜索空间的一个搜索个体,成虫的搜索范围较广、跳跃能力较强,负责种群全局搜索任务,幼虫的搜索范围较窄,负责种群的局部搜索任务。GOA的具体过程如下:
1)初始化种群规模N、种群位置Xi、最大迭代次数Tmax以及参数cmax和cmin,则
Xi=Si+Gi+Ai。
(7)
式中:Si表示种群个体之间对第i个个体的影响;Gi表示第i只蝗虫受到的重力影响;Ai表示第i只蝗虫受到的风力作用。计算式子为:
(8)
s(r)=fe-r/l-e-r。
(9)
式中:|xi-xj|表示第i只蝗虫与第j只蝗虫间的距离;s(r)表示蝗虫个体间的相互作用力,当s>0时,个体间相互吸引,当s<0时,个体间相互排斥;f、l分别表示吸引力度和吸引尺度,均为常数,本文取值f=0.5,l=1.5。则有
(10)
(11)
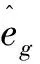
2)计算每只蝗虫个体的适应度函数值,并将最优蝗虫个体寄存在变量Ffit。
3)基于下式更新参数c,表达式为
(12)
式中t表示当前的迭代次数。
4)基于下式更新蝗虫个体的位置并计算每只个体的适应度值,表达式为
(13)
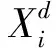
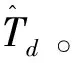
6)判断是否达到迭代终止条件,若是则返回最优个体,否则重复步骤3)~步骤5)。
GOA算法流程如图1所示。
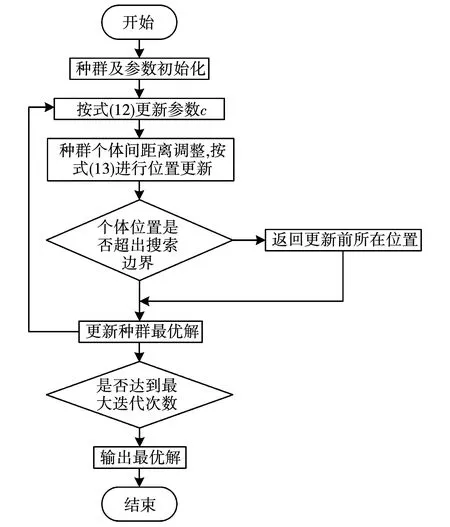
图1 GOA算法流程
2.2 长短时记忆网络
长短时记忆网络继承了循环神经网络的可记忆性功能,有利于读取信号序列的非线性特点,LSTM网络还引入了门控单元,从而解决长序列数据的长期依赖问题,避免网络训练过程中出现梯度消失或爆炸,以便保留每一循环单元的不同时间尺度信息特征[15-16]。LSTM单元结构如图2所示。
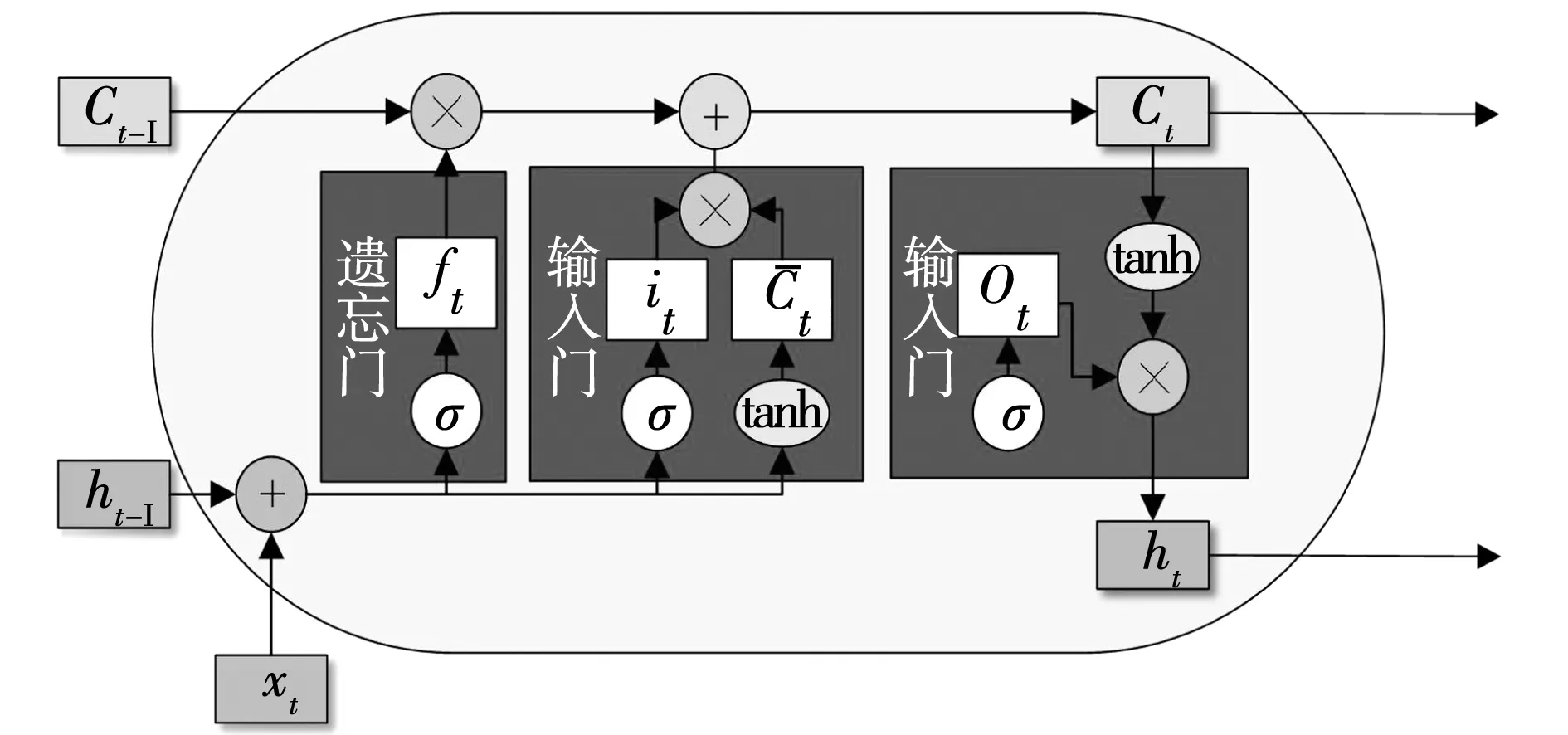
图2 LSTM的单元结构
LSTM网络的计算过程如下:
1)由遗忘门判断是否保留前一时刻细胞的状态信息Ct-1。遗忘门输入前一时刻的隐藏状态ht-1和新输入的数据Xt,输出遗忘门的值为
ft=σ(Wf[ht-1,xt]+bf)。
(14)
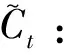
it=σ(Wi[ht-1,xt]+bi);
(15)
(16)
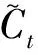
ht=ottanh(Ct);
(17)
Ot=σ(Wo[ht-1,xt]+bo)。
(18)
式中:Wf,Wi,Wc,Wo和bf,bi,bc,bo对应各门的权重矩阵和偏差;σ表示sigmoid函数。此处介绍的是前向LSTM,后向LSTM的基本结构与此相同,区别在于将原信号以倒序的方式输入网络。
2.3 双向长短时记忆网络
虽然LSTM网络记忆功能强大,能够提取历史序列中的有用信息,但其只能提取序列的前向信息,从而造成后向序列中的有用信息被浪费掉。Bi-LSTM是对LSTM的改进,该网络连接了一前一后两个反向的LSTM网络,使得模型的序列信息提取能力有了进一步提升。Bi-LSTM网络结构如图3所示,前传层训练前向序列,后传层训练后向序列,共同作用。

图3 Bi-LSTM网络结构
Bi-LSTM网络数学表达式为:
(19)
(20)
(21)
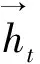
2.4 基于GOA优化的Bi-LSTM故障预测模型
利用Bi-LSTM模型进行预测时,超参数众多影响着模型的精度与效率,其中初始学习率α、隐藏层神经元个数m以及迭代次数H影响作用较大[17]。本文利用GOA算法对这3个参数进行迭代寻优,以增强模型的故障预测性能。基于GOA优化的Bi-LSTM电机轴承故障预测流程如图4所示,步骤如下:
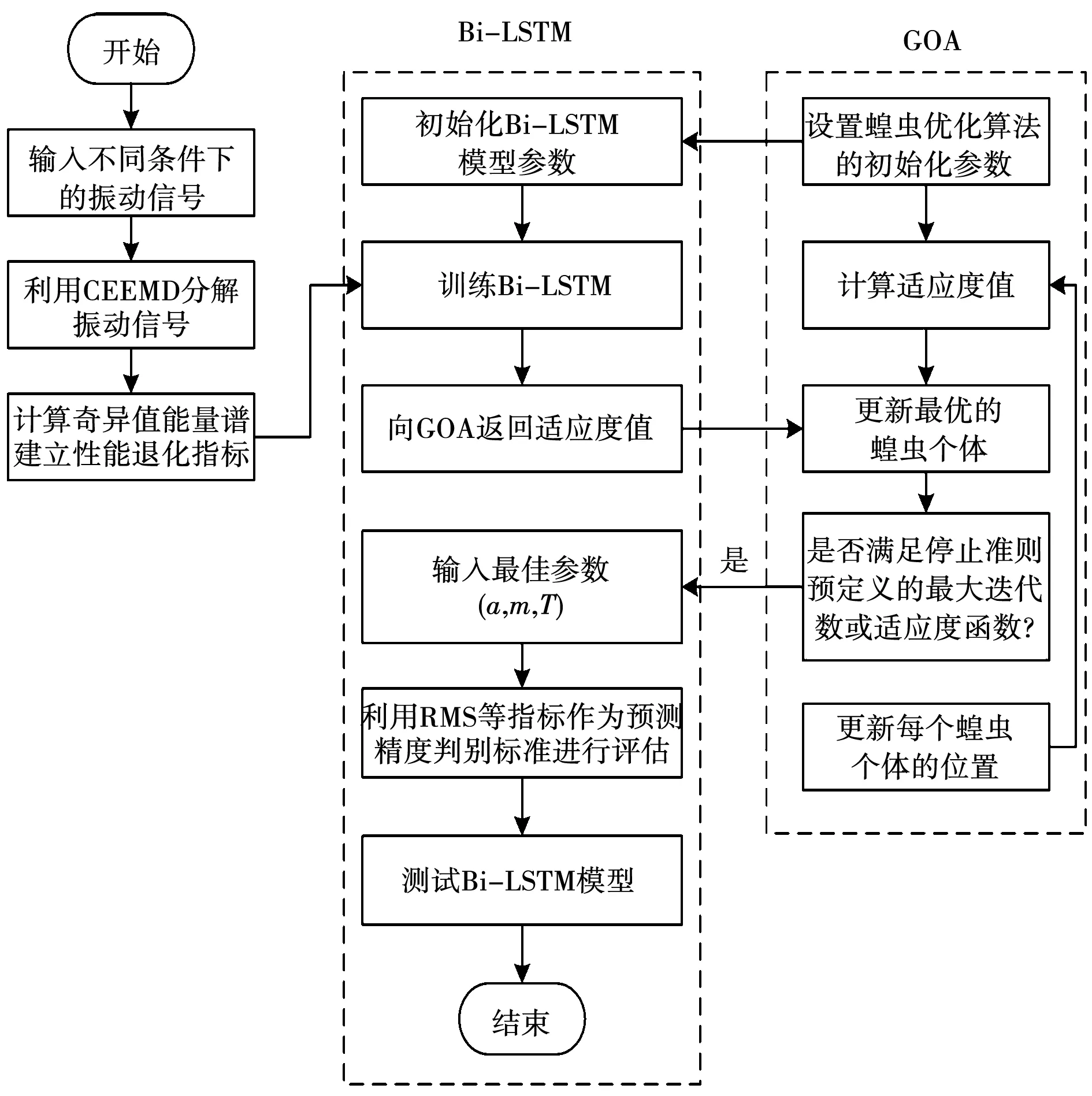
图4 电机轴承故障预测流程图
1)数据采集。在电机轴承的垂直方向和水平方向布置两个振动传感器,采集不同工况下的原始振动数据。
2)数据与处理。采集电机轴承的振动信号,利用CEEMD分解提取振动信号的IMF分量并进行归一化。
3)建立退化指标。计算每组IMF分量的奇异值并求其能量组成奇异值能量谱,并进行平滑去噪处理,将奇异值能量谱作为性能退化指标。
4)训练模型。将奇异值能量谱以一定比例分为训练集和测试集,基于训练集数据,以真实值与预测值的均方根误差为适应度值,利用蝗虫优化算法优化Bi-LSTM网络。
5)故障预测。将训练好的最优超参数代入Bi-LSTM网络,进行故障预测测试并与真实状态进行对比。
3 实例分析
为验证本文建立模型有效可行,使用辛辛那提大学轴承退化数据集[18]进行实验验证。该数据集振动信号的采样频率为20 kHz,采样周期为10 min,第一组实验包含4个轴承,本文选用3号轴承的振动数据,3号轴承共有2 156组振动数据,每组数据包含20 180个点,反映了3号轴承从正常运行到出现内圈严重故障,整个运行周期的振动信号。为了加快运算速度,这里提取每组数据的前10 000个点进行计算,得到信号波形如图5所示。
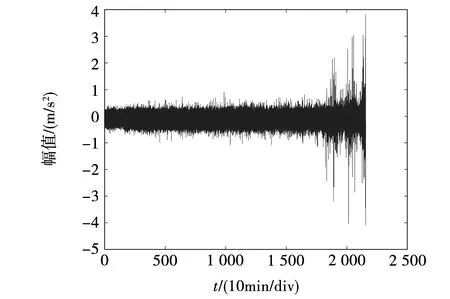
图5 振动信号波形图
3.1 建立性能退化指标
首先,利用CEEMD算法对轴承振动信号进行分解,得到10个IMF分量以及1个剩余分量。然后,计算各组IMF分量的奇异值能量,得到奇异值能量谱如图6所示,可以看出,数据中存在很多噪声,这会影响预测效果,于是对其进行平滑降噪处理,如图7所示。
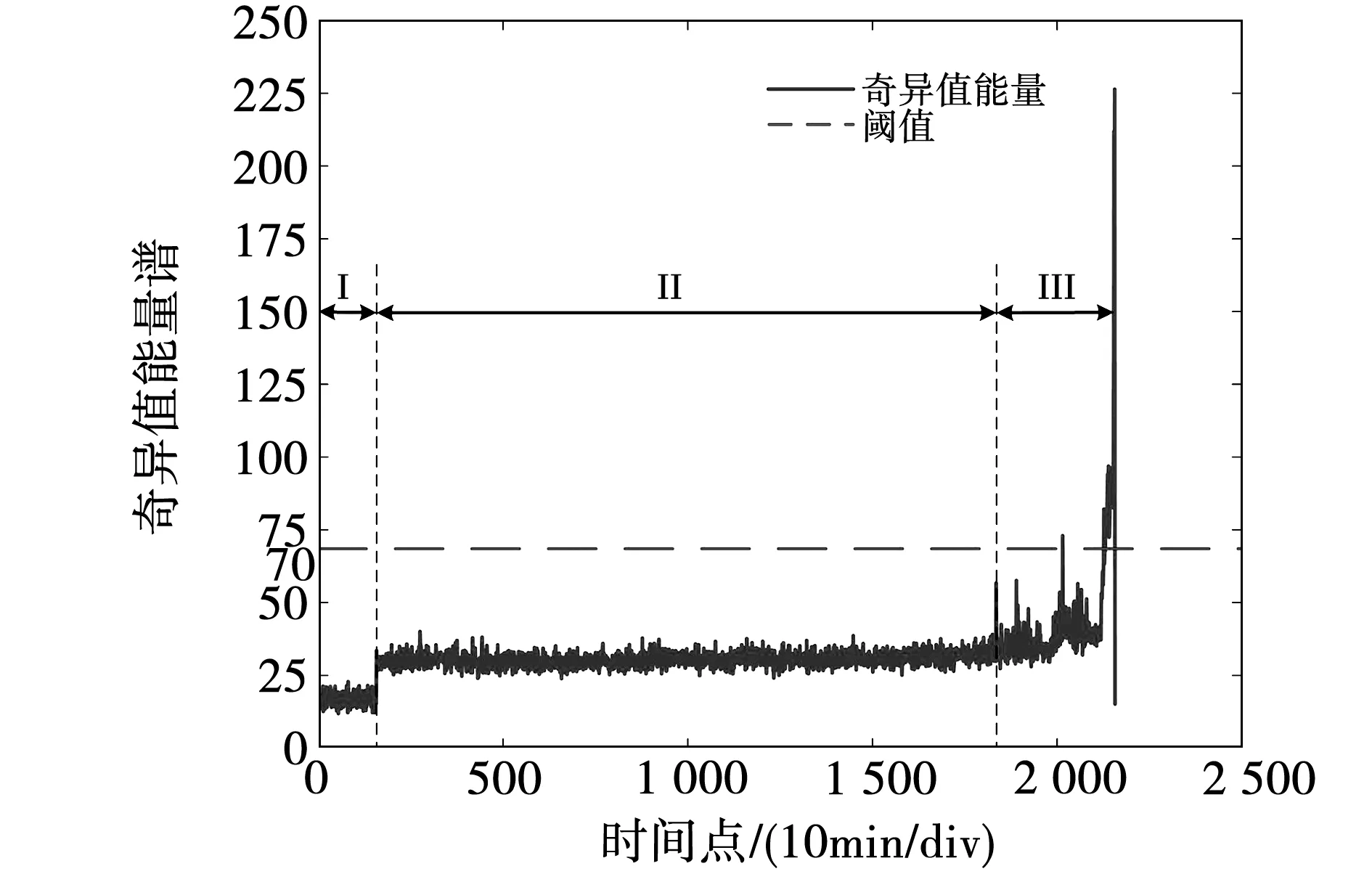
图6 原始信号奇异值能量谱
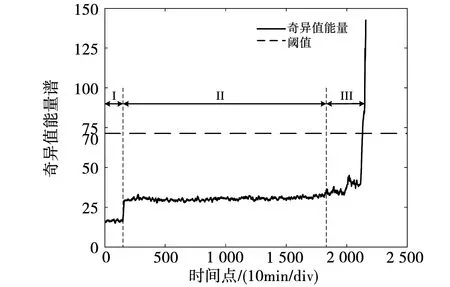
图7 降噪后的奇异值能量谱
轴承的时域振动信号近似呈高斯分布,由图6可知,电机轴承衰退过程中,在每个阶段其性能退化指标会出现局部差异的特点,可将整个周期的运行退化情况划分成三个阶段:阶段Ⅰ,实验刚起步,振动信号仅出现少量的频率成分,能量较为集中,奇异值分解结果也仅集中在少数成分上,求得奇异值能量较小,随时间变化非常稳定,轴承状态优良、运行稳定、未发生故障;阶段Ⅱ,轴承正常运转,局部奇异值能量时而出现不合理的波动,表示在其工作过程中可能出现机械整体抖动或是轻微磨损的情况,属于正常现象,利用Bi-LSTM模型进行故障预测是基于时序信号的整体趋势,出现这种现象并不会影响预测的效果;阶段Ⅲ,随着波动频率增多,此时轴承磨损加重,信号中出现了复杂的故障频率与共振频率,信号的能量以及分解的奇异值也随之分散,导致奇异值能量增大,轴承处于性能衰退期,故障程度也随之加剧。根据实验经验,设置故障阈值为70,奇异值能量超过阈值则被认定为严重故障,为避免振动信号出现波动或误采样的情况,规定指标超过阈值5次,电机停机进行检修。
3.2 基于GOA的超参数优化
由于电机在运行至21 560 min时轴承故障程度已经加剧,应当更早地停止运行,因此在故障加剧后的数据不具有预测意义,选取第1 900组到2 125组的数据作为训练集,第2 126组到2 150组的数据作为测试集。利用训练集数据训练GOA-Bi-LSTM模型,蝗虫优化算法初始参数如表1所示,为了比较GOA算法的优越性,这里同时使用鲸鱼优化算法(whale optimization algorithm,WOA)进行优化,依据经验设置WOA的参数,以均方根误差(root mean square error,RMSE)作为适应度函数,其随迭代次数变化曲线如图8所示。获得最优超参数为:初始学习率α=0.003、隐藏层神经元个数m=152以及迭代次数H=237。
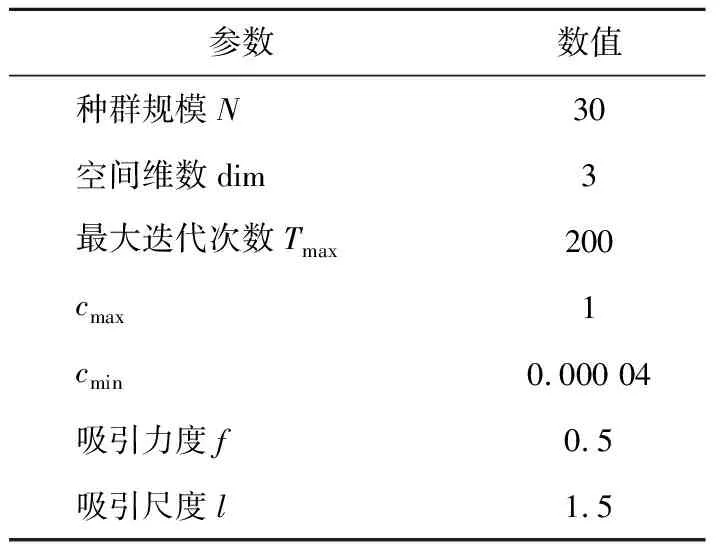
表1 GOA参数
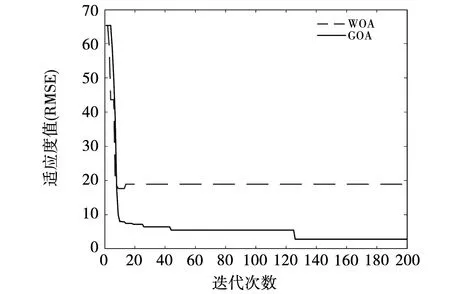
图8 迭代寻优过程
由图8可得,GOA算法在迭代进行到第20代时开始有了较好的收敛效果,WOA算法在第13次迭代时开始了收敛,收敛速度较快,但其收敛时未达到最低适应度值,说明WOA算法容易陷入局部最优解。其次,GOA算法在收敛时的均方根误差也较小,表明其预测精度更优。
3.3 故障预测模型对比
利用训练好的Bi-LSTM网络进行一步迭代预测,在进行每一次预测时,将前一次预测的结果加在当前输入的结尾,预测结果如图9所示。
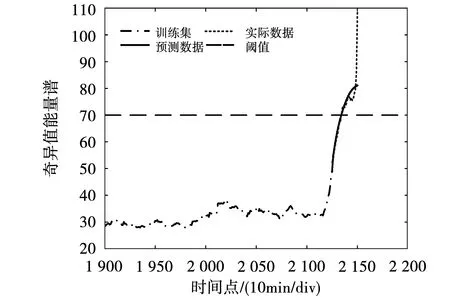
图9 GOA-Bi-LSTM故障预测结果
为验证本文所建立模型的优越性,选取极限学习机(extreme learning machine,ELM)、时滞性支持向量回归(time delay support vector regression,TD-SVR)模型、深度卷积神经网络(deep convolutional neural network, DCNN)模型进行对比实验,数据集划分与本文完全相同,参数设置完全依照经验数据,预测结果如图10~图12所示。
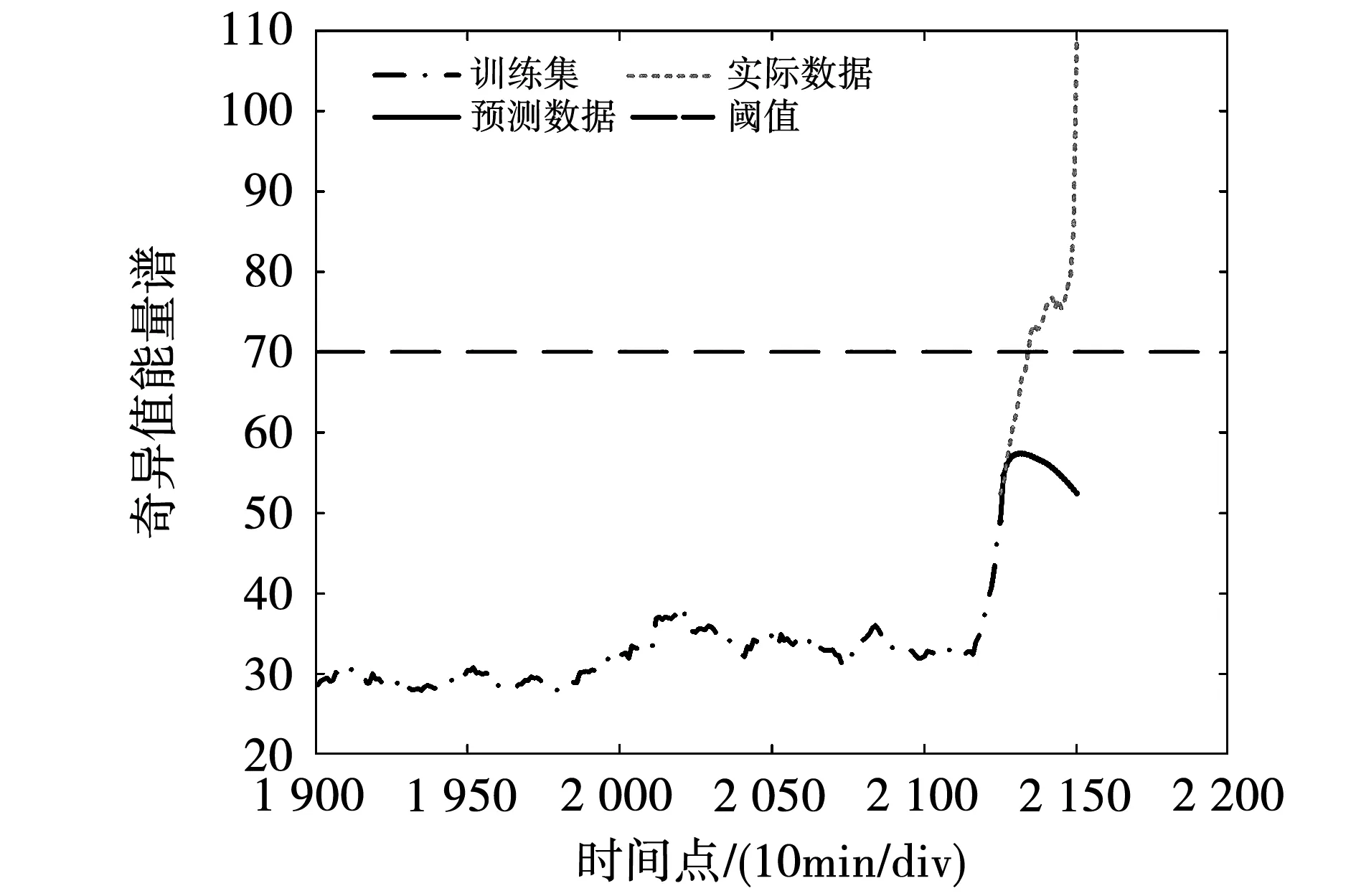
图10 ELM故障预测结果
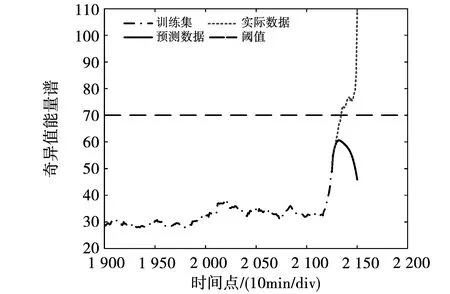
图11 TD-SVR故障预测结果
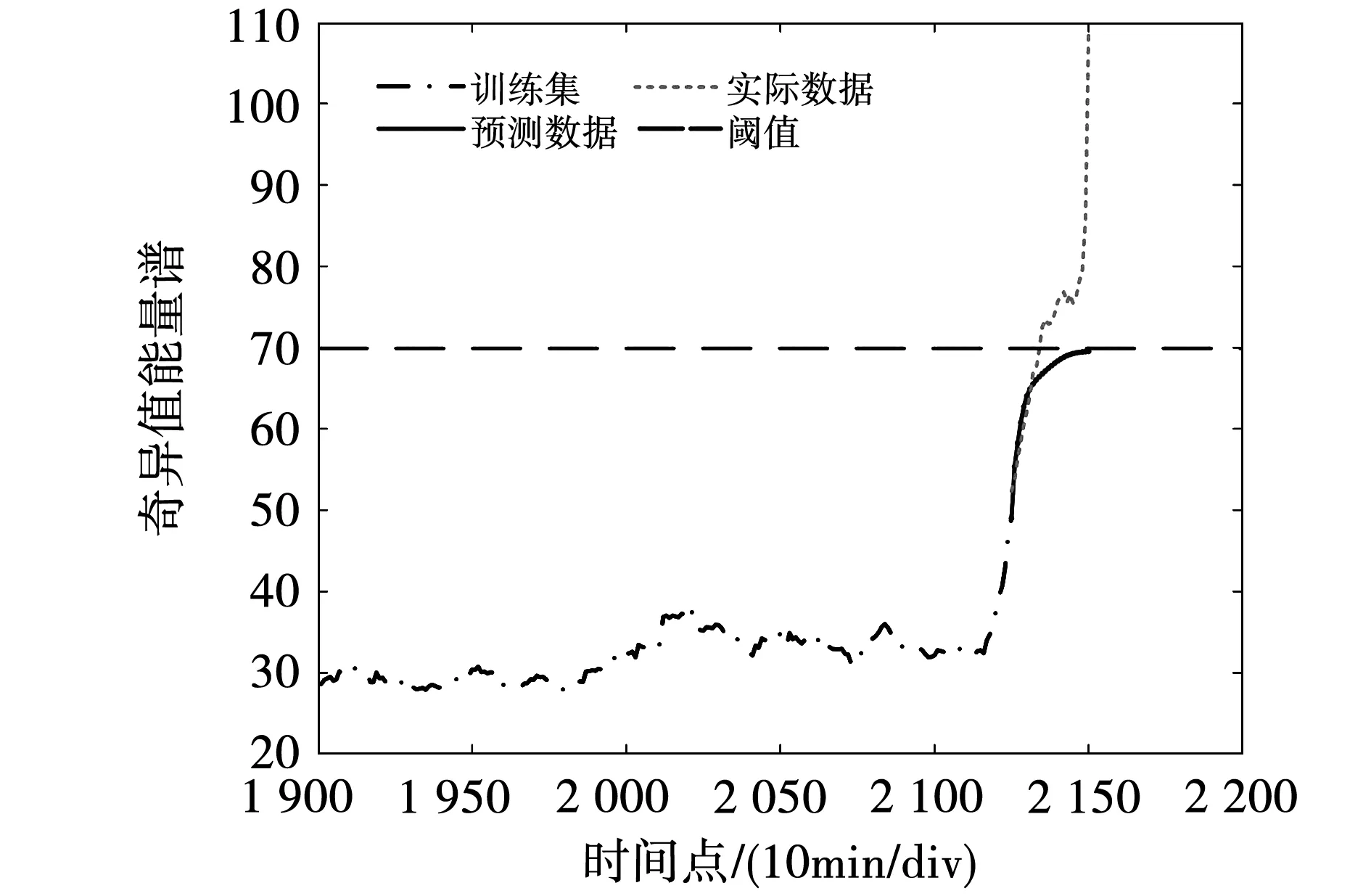
图12 DCNN故障预测结果
从图9~图12可以直观地看出,本文所建立的模型预测精度要优于其他模型的精度。为了准确评估模型预测的精度,本文利用RMSE和那什系数(Nash-Sutcliffe efficiency coefficient, NSE)作为评估标准,表达式为:
(22)
(23)
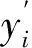
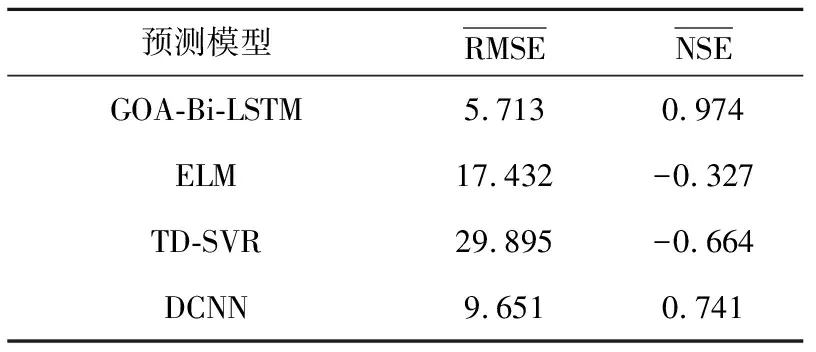
表2 预测结果对比
由表2可以看出,相较于ELM、RD-SVR、DCNN模型,本文所提模型的NSE值最接近于1,RMSE值最小,仅有5.713,说明GOA-Bi-LSTM的拟合效果最好,相比于ELM、TD-SVR、DCNN模型在电机轴承故障预测领域的预测精度最高。
3.4 预测容错性分析

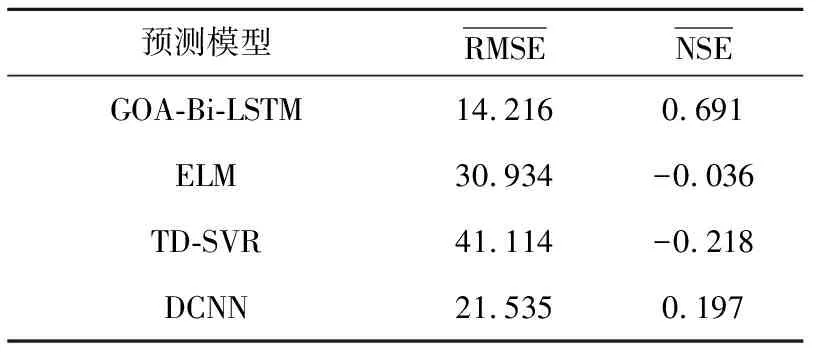
表3 误采样对预测结果的影响
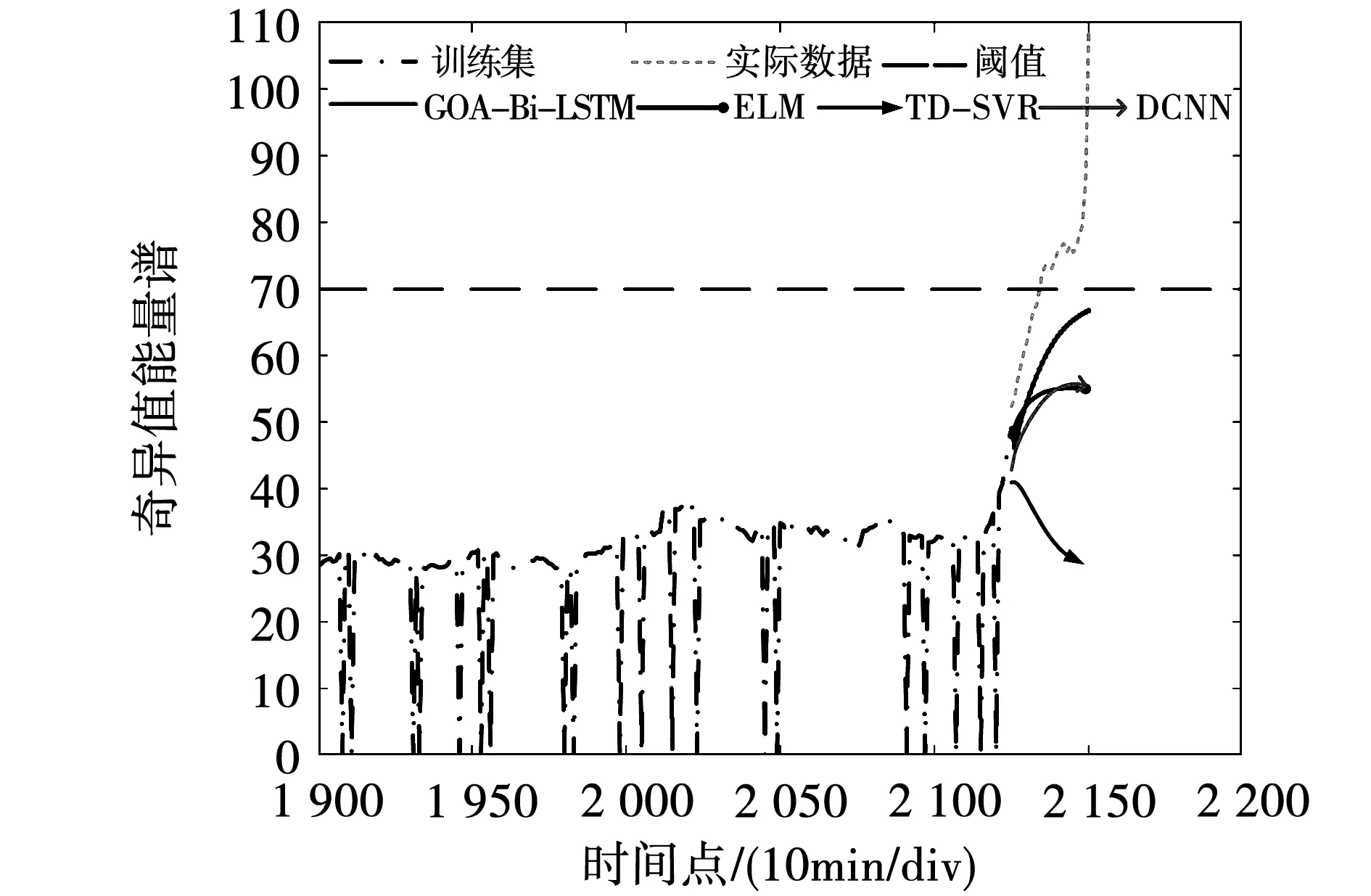
图13 容错性分析预测结果
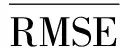
4 结 论
本文建立了一种基于GOA优化Bi-LSTM模型的电机轴承故障预测方法。首先,利用CEEMD分解振动信号,提取振动信号的特征分量并计算奇异值能量谱构造性能退化指标;其次,利用GOA对Bi-LSTM网络进行优化返回最优超参数;最后,利用优化好的Bi-LSTM网络实现电机轴承的故障预测,得到结论如下:
1)利用奇异值能量谱作为性能退化指标,能够很好地体现出电机轴承状态的变化趋势,能够间接反应电机轴承的故障变化。
2)利用蝗虫优化算法对双向长短时记忆网络的超参数进行优化,蝗虫优化算法相较于鲸鱼优化算法具有更高的收敛精度。
3)针对LSTM网络处理前向序列,仅考虑前向信息而忽略了后向信息的情况,提出Bi-LSTM网络,具有一前一后两个互补的LSTM网络,分别处理时间序列的前向和后向信息,提高了模型信息提取能力。
4)基于开源数据集,将本文模型与ELM、TD-SVR、DCNN模型进行对比分析,本文模型具有更高的预测精度以及更强的鲁棒性。
