交流输电线路交叉跨越区域下方电场影响因素研究
2022-07-15宋福根吕学伟
宋福根, 吕学伟
(福州大学 电气工程与自动化学院,福建 福州 350000)
0 引 言
特、超高压交流输电技术不仅可以超远距离输电,还可以降低外界干扰、减少输电过程中的资源浪费,因此是未来电力系统的必然发展趋势[1-4]。但由于土地走廊的限制,高压交流输电线路建设不可避免地出现了交叉跨越的情况。而高压电场产生电场环境问题对下方的人类活动有不可忽视的影响,且交叉跨越区域的电场分布更为复杂。因此,研究高压交叉跨越输电线路下方区域的工频电场问题[5-7]是十分必要和重要的,分析导线离地高度、相序、交叉角度、相位差、排列方式等因素对下方区域近地面1.5 m(人类活动一般高度)平面内电场强度的影响规律,并提出减小下方区域近地面电场强度或改善下方电场分布的措施,可为交叉跨越区域线路的电场环境影响评价、治理及设计规划提供一定参考,也可提高公众对交叉跨越高压输电工程的认可程度,具有重要的现实意义和工程应用价值。
对于交叉跨越导线产生的工频电场,由于存在两条高压输电线路的影响,必须建立三维模型计算求解[8-12]。因此,本文利用基于有限元原理的Ansys仿真软件建立高压输电线路交叉跨越区域等比例三维空间模型,来计算交叉跨越下方区域近地面1.5 m高度内沿各条观测线的电场强度分布,并分析导线离地高度、相序、交叉角度、相位差、排列方式等因素对该平面内电场强度分布的影响规律,进而研究如何降低或改善交叉跨越线下区域的电场强度。本文研究成果一方面有助于科学合理地削弱交叉跨越线路产生的工频电场,将其大小控制在国家规定的允许范围内,并改善下方电场的整体分布;另一方面,可为输变电工程建设中的设计规划提供理论参考。
鉴于现有文献对于交叉跨越区域下方电场强度的影响因素分析存在一些不足之处[13-15],即只观察交叉跨越双方导线一条角平分线路径上的电场分布规律,来研究不同因素对近地面1.5 m高度内电场强度的影响规律,或是研究的影响因素不够全面,虽然其结果有一定意义,但全面性、严谨性、说服力略显不足。因此,本文在1.5 m平面内设置了4条观测线(沿1 000 kV中间相导线方向、沿500 kV中间相导线方向以及沿双方导线交叉角平分线),这4条观测线最具有代表性且几乎覆盖了整个1.5 m空间,相比于单条观测线,更能够说明整个平面的电场分布规律,同时研究的影响因素有导线离地高度、相序、交叉角度、相位差、排列方式等,全面分析4条观测线上不同因素对下方1.5 m高度内电场强度的影响规律,并给出减小或改善下方区域电场强度的方法。
1 1 000 kV与500 kV交叉跨越模型
1.1 交叉跨越区域三维空间电场理论计算
由静电场理论可得线电荷对空间任意一点产生的电场强度[16]的表达式为
(1)

线电荷l1、l2分别为平行Z轴、垂直于Y轴的长直导线,设其坐标分别为:
(2)
(3)
则l1、l2对任意一点P(x,y,z)的三维空间电场强度分别为E1、E2,表达式为:
(4)
令
(5)
则式(4)可表示为:
(6)
1.2 交叉跨越区域模型参数及观测线设置
由于实际的交叉跨越区域高压输电线路较为复杂,且部分参数、因素、结构的影响很小,可以忽略不计,因此本文对交流高压输电线路交叉跨越区域工频电场三维计算模型作如下简化[17]:
1)将交变电场看作准静态场;
2)地面及无穷远处取零电位;
3)忽略导线弧垂,看作长直导线;
4)分裂导线等效为单导线;
5)忽略除导线外其他物体对电场的影响;
6)忽略端部效应;
7)忽略跨越双方线路的感应电压。
基于上述简化,利用Ansys仿真软件建立交流高压输电线路交叉跨越区域工频电场三维计算模型,如图1所示。模型参数如表1所示。
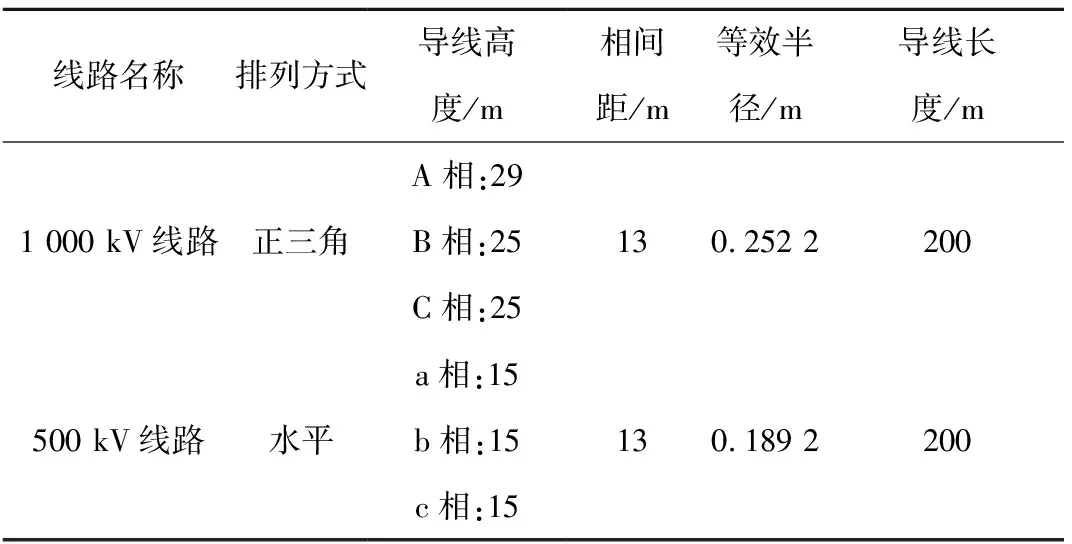
表1 交叉跨越区域工频电场三维仿真模型参数
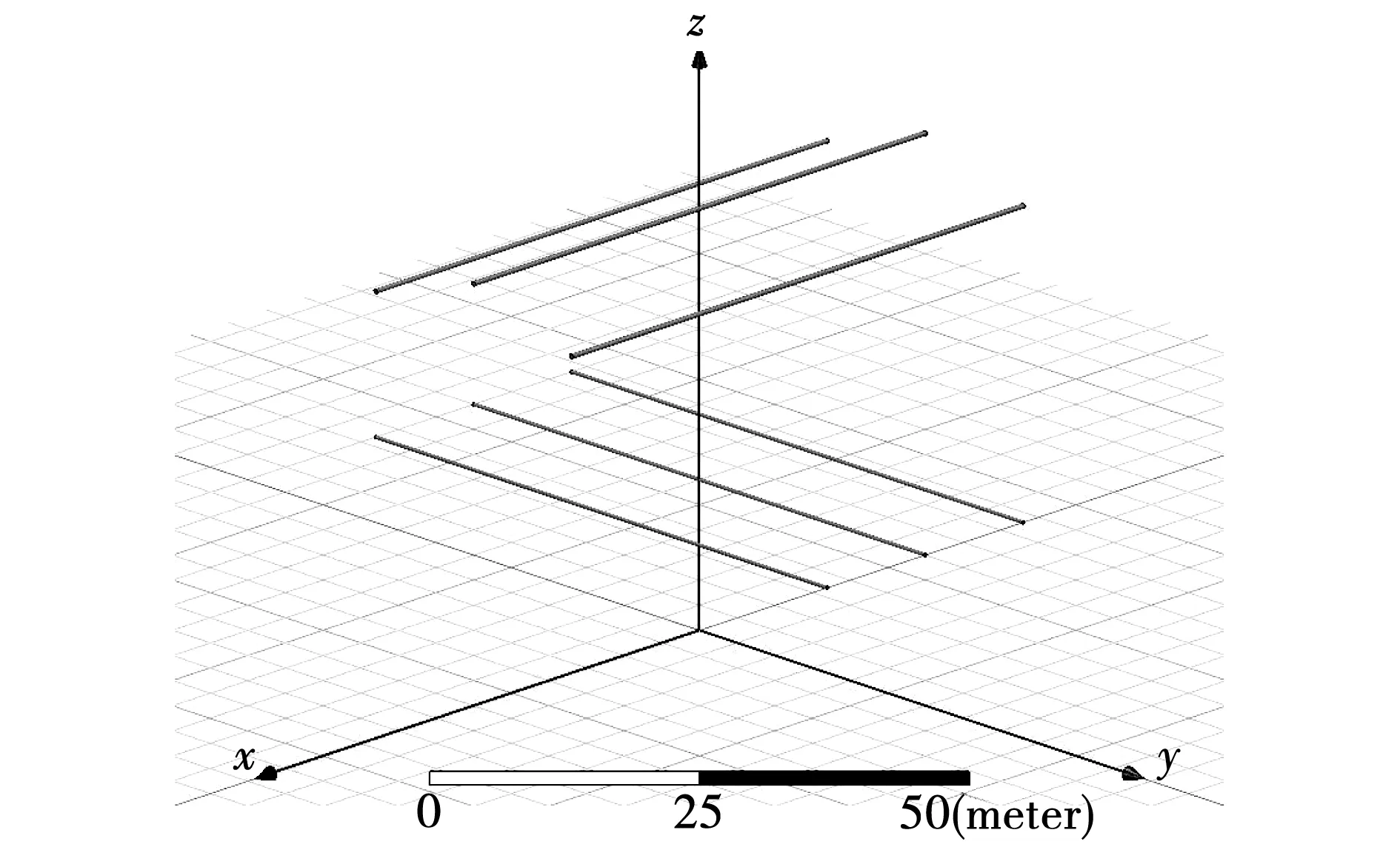
图1 交叉跨越区域工频电场三维仿真模型
本文选取1.5 m高度平面内4条观测线L1~L4,其中L1沿1 000 kV线路中间相导线方向,L2沿500 kV线路中间相导线方向,L3和L4为双方导线的两条交叉角平分线投影,其俯视示意图如图2所示。可以看出,这4条观测线最具有代表性且涵盖了1.5 m平面的竖直、水平、交叉各个方向,因此相比于现有文献的1条角平分线观测路径,更能代表整个平面内的电场强度变化情况。
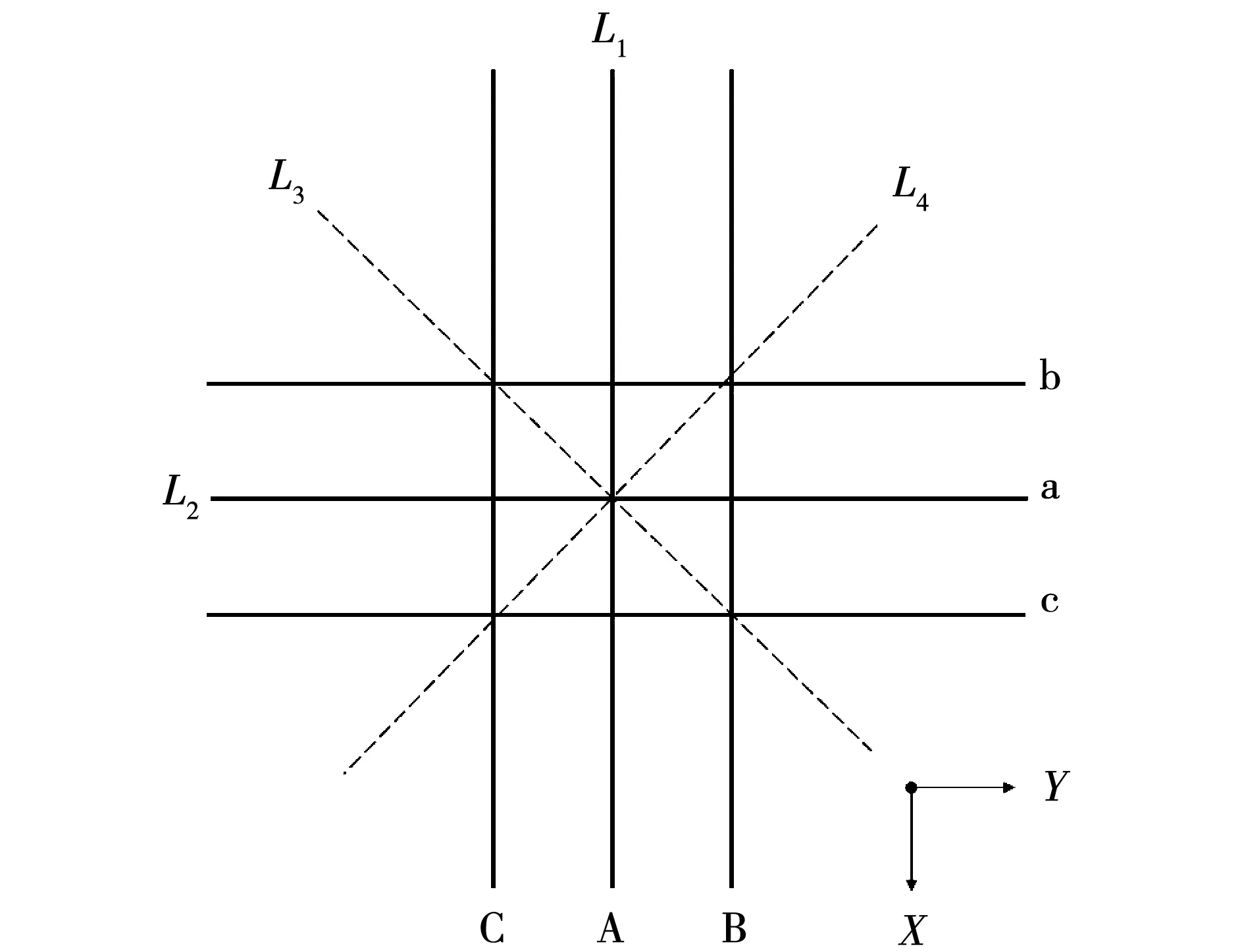
图2 1.5 m平面内预设观测线俯视示意图
由于三相交流输电线路仿真计算得到的是任意时刻的电场强度瞬时值,且因为导线表面的电场均为法向方向。因此,为了描述交叉跨越区域在静态场中的电场分布,本文分别取t=0和t=T/4时的三相交流输电线路额定运行电压为激励,得到两个时刻的电场强度计算结果,并求其均方根值,即可得到交叉跨越区域在静态场中沿各条观测线的电场强度有效值分布。
2 下方区域电场强度影响因素分析
对已建立的三维仿真模型进行工频电场仿真分析,得到不同因素影响下4条观测线上的电场强度随距离的变化趋势,并进行对比分析,得出不同因素对交叉跨越区域下方区域(主要研究1.5 m高度空间)电场强度的影响规律,相对应地提出改善下方区域电场的措施。
由于国标对于输电线路下方离地1.5 m高度附近的电场强度有规定限值,即该平面内的电场强度最大值不得超过国标限值。因此,研究如何降低该平面内的电场强度最大值,即对4条观测线上的电场强度最大值进行比较,确定整个平面的电场强度最大值。基于此最大值,分析各个因素对其造成的影响,给出降低该最大值的措施。
2.1 导线对地高度影响分析
2.1.1 1 000 kV导线对地高度影响分析
保持500 kV导线高度和其他参数不变,从最低高度25 m开始按照3 m为间隔提高1 000 kV边相导线高度至37 m(中间相导线也相应提高),分析1 000 kV导线不同高度(分别为25、28、31、34、37 m)情况下,4条观测线上电场强度的变化趋势,如图3所示。可以看出,1 000 kV导线高度不影响各路径上的电场强度变化趋势,也不改变其对称性和极值点位置(3个极值点均位于导线交叉点投影附近)。
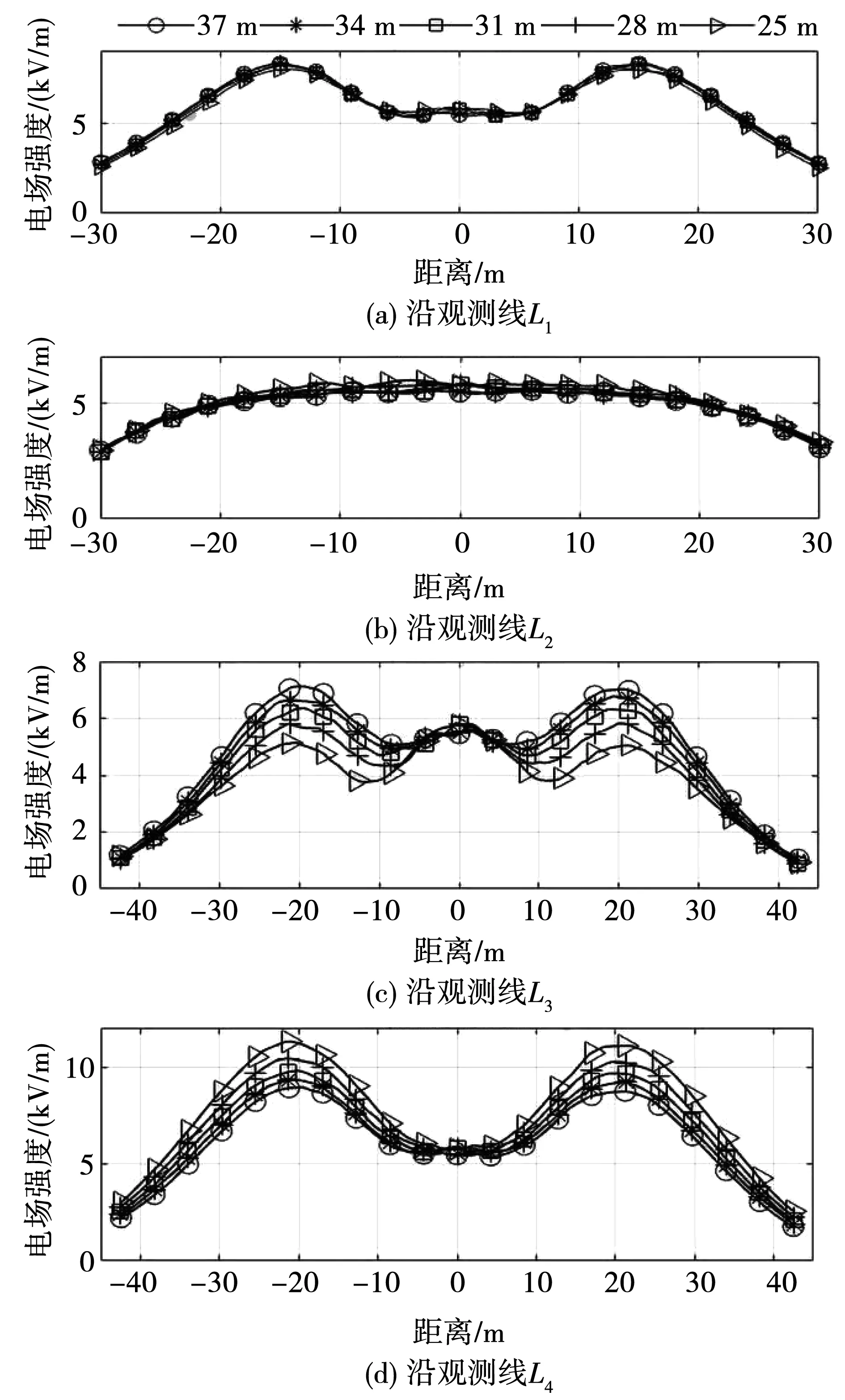
图3 1 000 kV导线不同高度下电场强度变化趋势
随着1 000 kV导线高度提高,观测线L1、L2路径上的电场强度略微有所变化,但幅度不大;观测线L3路径上的电场强度明显增大;而观测线L4路径上的电场强度却明显减小。
为进一步量化结果,得到1 000 kV导线不同高度下4条观测线上电场强度的平均值及最大值,如表2所示,单位:kV/m。由表2可得,当1 000 kV导线高度升高12 m,L1沿线电场强度平均值仅增大3.07%,最大值仅增大4.37%;L2沿线电场强度平均值仅减小4.84%,最大值仅减小6.95%;而L3沿线电场强度平均值增大27.43%,最大值增大23.17%;L4沿线电场强度平均值减小20.09%,最大值减小20.72%。
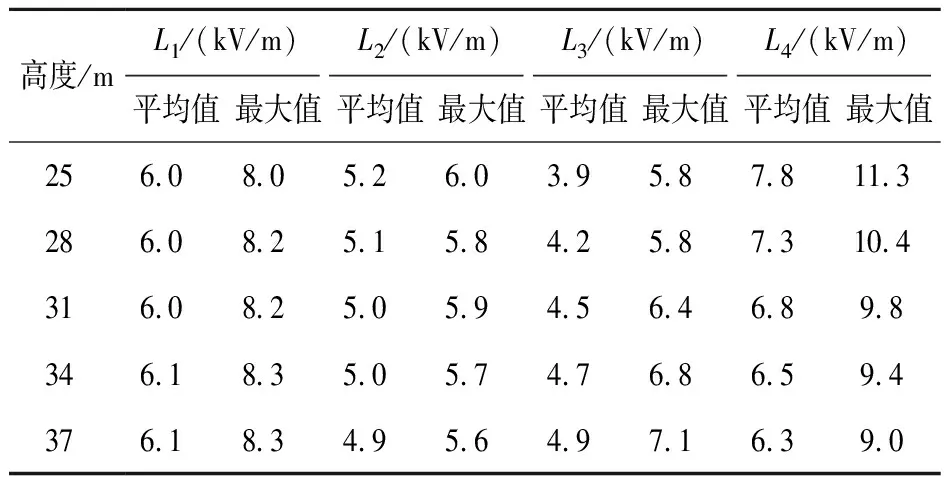
表2 1 000 kV导线不同高度下电场强度平均值及最大值
2.1.2 500 kV导线对地高度影响分析
保持1 000 kV导线高度为37 m和其他参数不变,提高500 kV导线高度,分析500 kV导线不同高度(分别为15、18、21、24、27 m)情况下,4条观测线上电场强度的变化趋势,如图4所示。可以看出,随着500 kV导线高度提高,观测线L1、L2、L3、L4路径上的电场强度均明显减小。
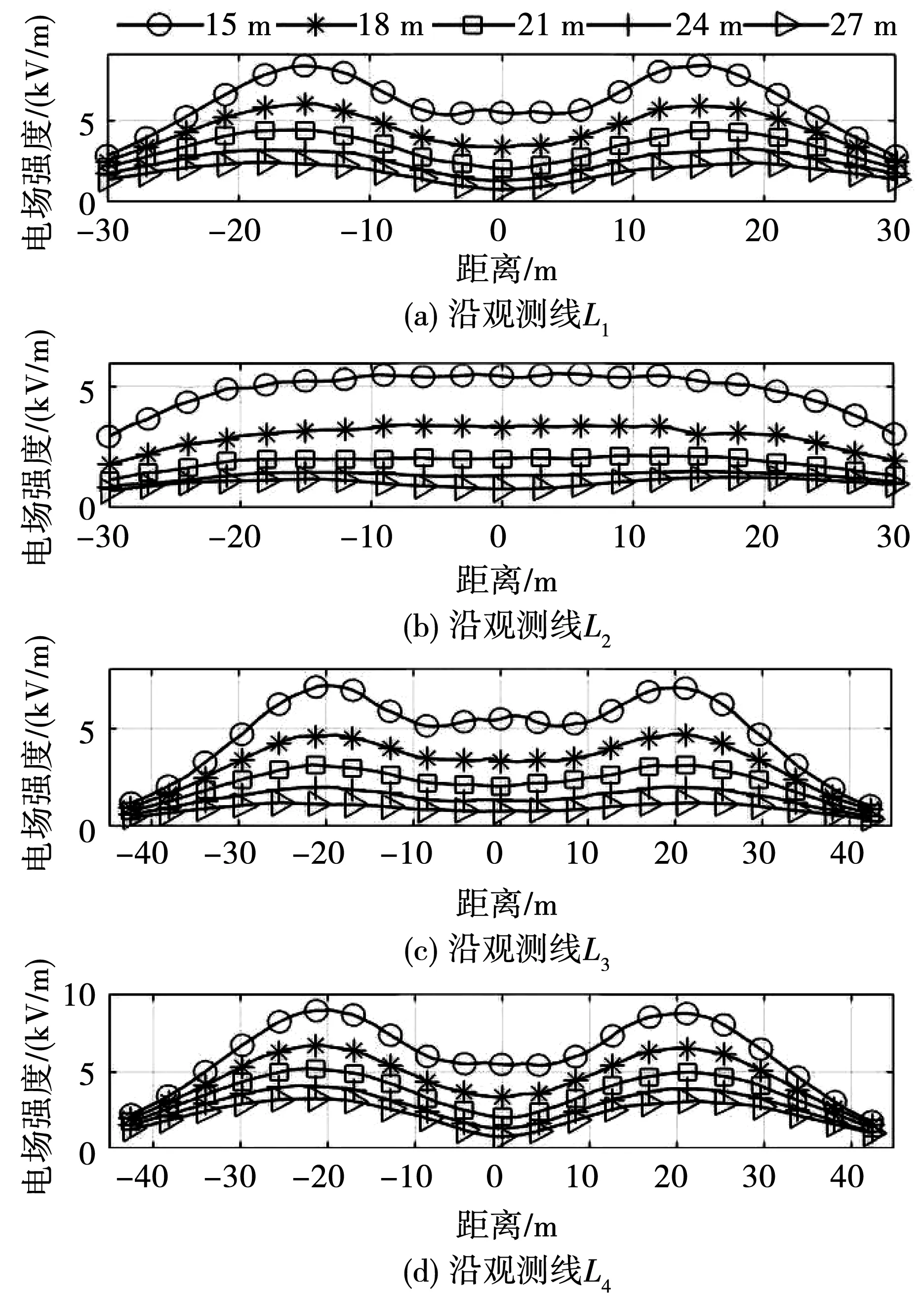
图4 500 kV导线不同高度下电场强度变化趋势
量化得到500 kV导线不同高度下4条观测线上电场强度的平均值及最大值,如表3所示,单位:kV/m。由表3可知,当500 kV导线上升12 m,4条观测线上的电场强度平均值和最大值均大幅度减小,减小幅度在63.85%~92.00%之间。
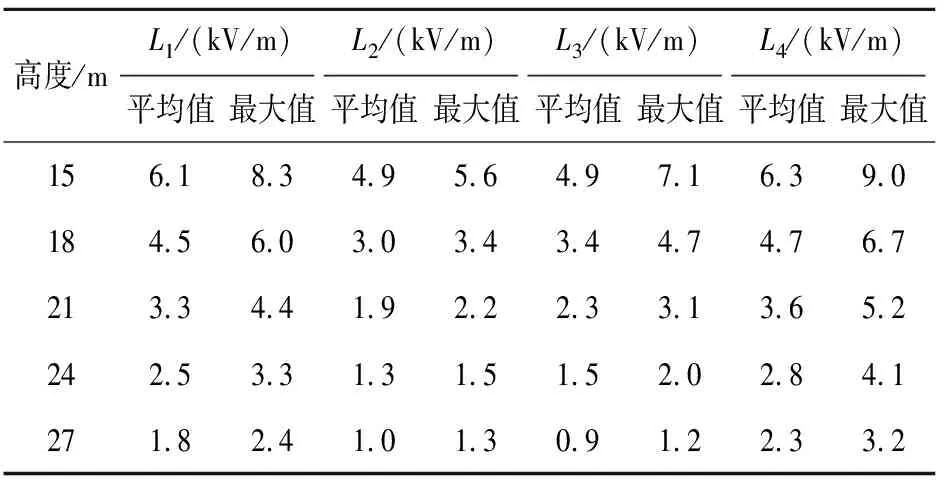
表3 500 kV导线不同高度下电场强度平均值及最大值
综上,从整体的电场强度分布变化趋势来看,导线高度对下方区域电场强度有明显影响,但不改变其变化趋势、对称性、极值点位置等特性。其中,500 kV导线高度对4条观测线上(即整个平面)的电场强度有明显影响,电场强度随着500 kV导线高度的提高而减小,由于单独作用时其电场强度也随导线高度升高而减小,说明500 kV导线对交叉跨越区域下方电场强度呈正向叠加作用。1 000 kV导线高度对L1、L2路径上的电场强度影响不大,L3路径上的电场强度却随1 000 kV导线高度升高而增大,L4路径上的电场强度随1 000 kV导线高度升高而减小,同理可以说明1 000 kV导线对L3路径上的电场强度呈反向叠加作用,对L4路径上的电场强度呈正向叠加作用。可用简单的公式来表示交叉跨越区域下方合成场强与双方导线单独作用时的场强的叠加关系,表达式为:
(7)
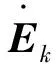
经过分析可知,通过提高500 kV导线能够有效降低平面内的整体电场强度,即可改善交叉跨越区域下方电场分布;提高1 000 kV导线也能整体降低下方区域的电场强度(除L3路径),虽然L3路径上的场强变化情况相反,但由于L3路径上的电场强度整体水平均低于L4路径。因此从总体上来说,提高1 000 kV导线线高仍可改善交叉跨越下方区域电场分布。
若从整个平面内的电场强度最大值来考虑,从图3和图4中可以发现,4条观测线路径中,L4观测线上的电场强度最大值是最大的。因此要研究减小电场强度最大值的措施,只需分析导线高度对L4观测线上的电场强度最大值的影响规律即可。随着1 000 kV导线高度和500 kV 导线高度的升高,L4观测线上的电场强度最大值均有所减小,且高度越高,其效果越不明显,另外500 kV导线高度升高造成的电场强度减小幅度更为明显。因此,可通过提高双方导线的对地高度来降低交叉跨越区域下方离地1.5 m空间的电场强度最大值,但随着高度越高,其效果越不明显;另外,提高1 000 kV导线高度降低电场强度的效果略逊于500 kV导线。
2.2 相序影响分析
2.2.1 1 000 kV线路相序影响分析
保持500 kV线路相序为abc及其他参数不变,改变1 000 kV的相序,分析不同相序(分别为ABC、ACB、BAC、CAB、BCA、CBA)情况下,4条观测线上电场强度的变化趋势,如图5所示。可以看出:
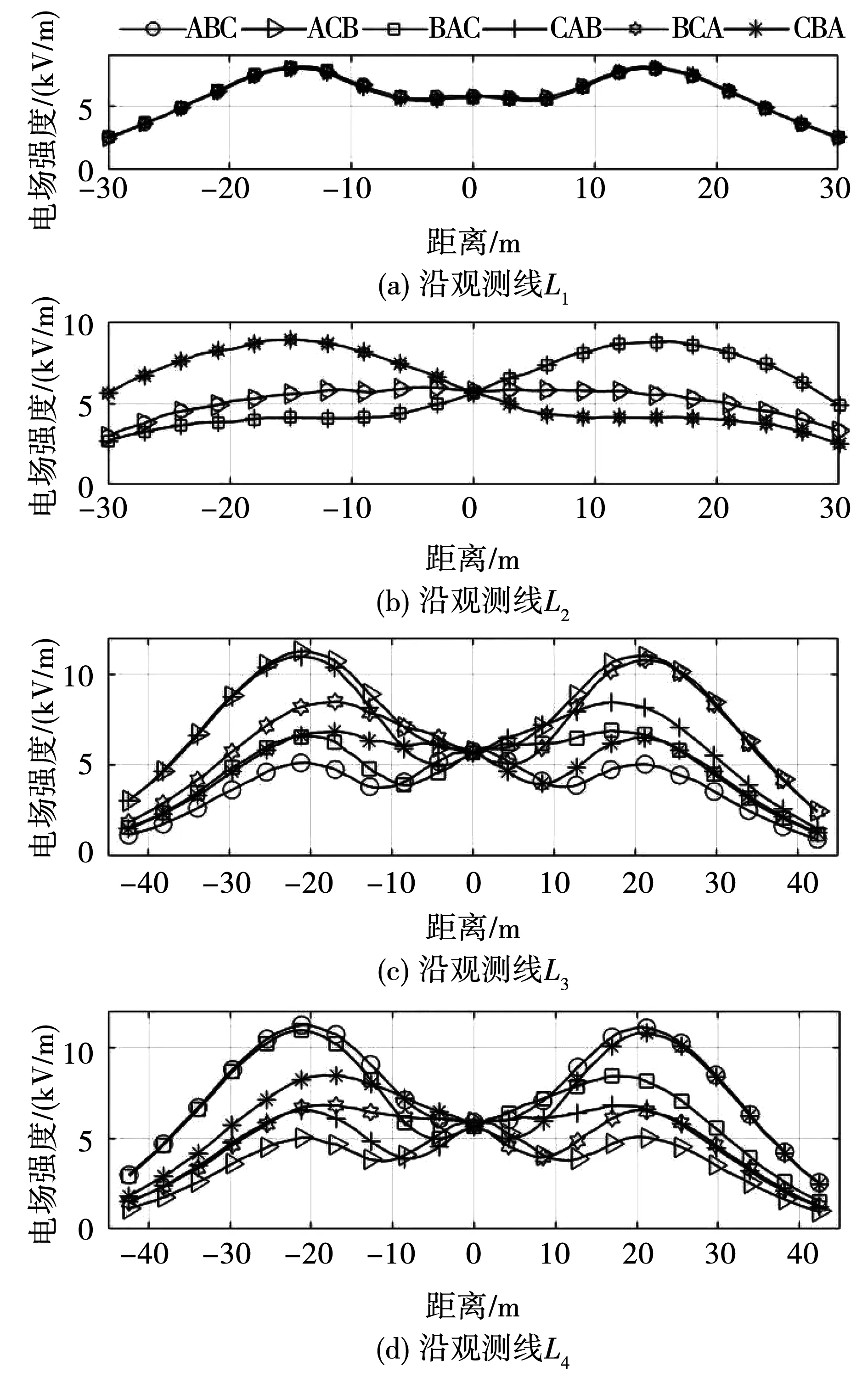
图5 1 000 kV线路不同相序下电场强度变化趋势
1)观测线L1路径上,不同相序下电场强度一致,1 000 kV相序对L1上的电场强度无影响;
2)观测线L2路径上,1 000 kV相序为ABC和ACB时,电场强度分布趋势一致,均为“中间高、两边低”;相序为BAC与CAB时,电场强度分布趋势一致,均为“左低右高”;相序为BCA与CBA时,电场强度分布趋势一致,均为“左高右低”。由于电场强度极大值点均位于导线交叉点附近,因此观察交叉点处的相导线组合情况,相序为ABC和ACB时,3个交叉点处的相序交叉情况分别为Ca、Aa、Ba和Ba、Aa、Ca,再结合这两种相序情况下的电场强度趋势为中间高、两边低,可以看出,电场强度最高处为同相导线交叉处(Aa);相序为BAC与CAB时,交叉点处分别为Ca、Ba、Aa和Ba、Ca、Aa,根据同相导线交叉处(Aa)的电场强度最高原理,符合“右高”的趋势;相序为BCA与CBA时,交叉点处分别为Aa、Ba、Ca和Aa、Ca、Ba,同样由于同相导线交叉处(Aa)的电场强度最高,符合“左高”的趋势。因此得出:同相导线交叉处的电场强度最高;
3)观测线L3路径上,相序为ACB时电场强度最大值最大,且电场强度整体均最大,其交叉点处为Bb、Aa、Cc;相序为CAB时,电场强度最大值最大,且位于左边,其交叉点处为Bb、Ca、Ac;相序为BCA时,电场强度最大值最大,且位于右边,其交叉点处为Ab、Ba、Cc。而其他相序情况电场强度均较低,其中与500 kV线路abc相序互为同序排列的ABC情况下的电场强度最大值最小(由于中心交叉点出的电场强度均保持不变,因此在对比时不考虑该点的电场强度),由此也可说明同相导线交叉处的电场强度最高;
6种不同相序情况下L3观测路径上的导线交叉点情况示意图如图6所示(其他情况同理,此处不作详述)。
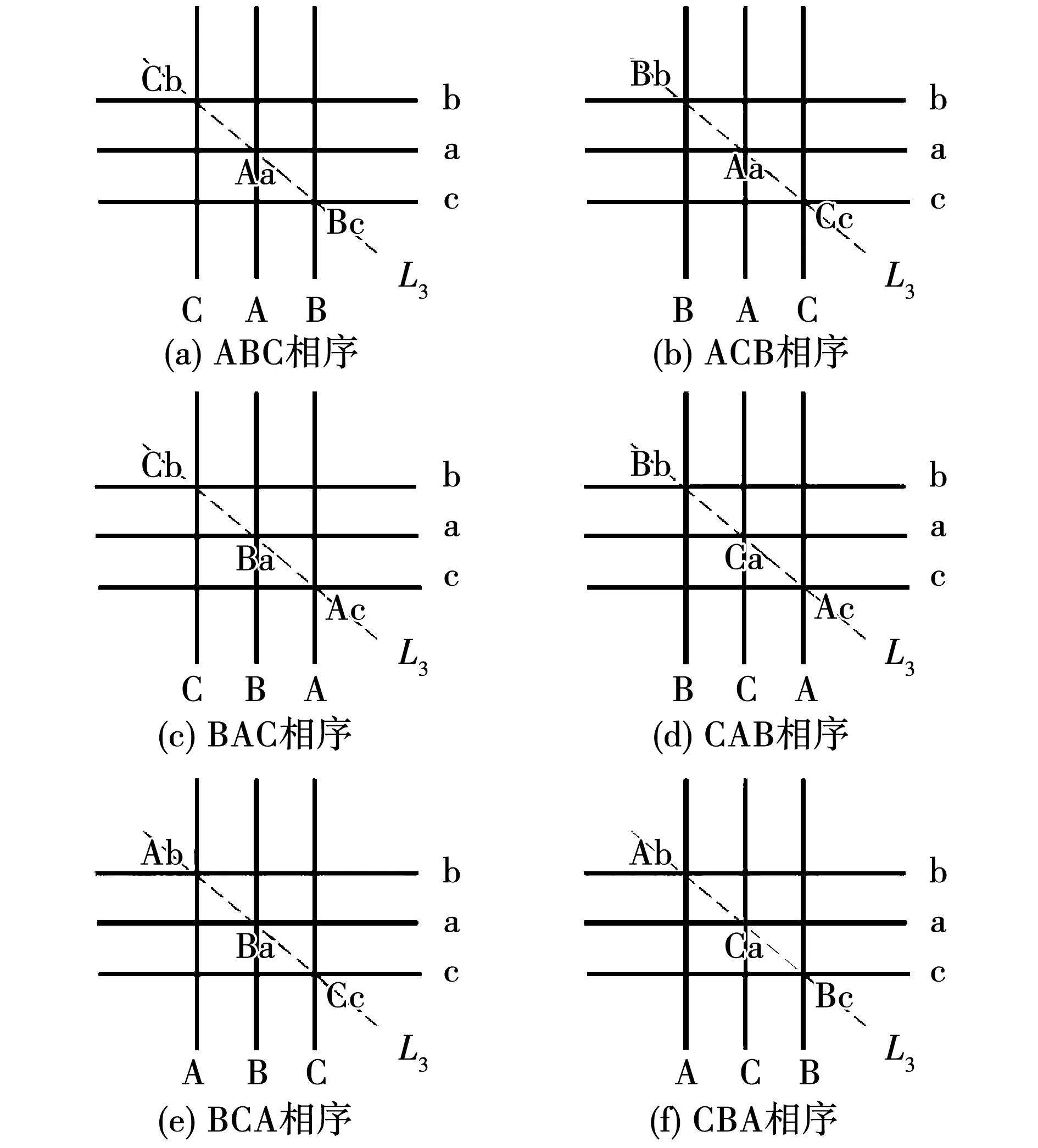
图6 1 000 kV不同相序情况下L3路径上导线交叉点情况示意图
4)观测线L4路径上的电场强度随相序不同的趋势与L3表现结果相反的是:相序为ABC时电场强度最大值最大,相序为BAC时电场强度最大值也最大,且位于左边,相序为CBA时电场强度最大值也最大,且位于右边;而逆序排列的ACB情况下的电场强度最大值最低。虽然表现结果不同,但其原理仍是同相导线交叉处的电场强度最高。
量化得到1 000 kV导线不同相序下4条观测线上电场强度的平均值及最大值,如表4所示,单位:kV/m。
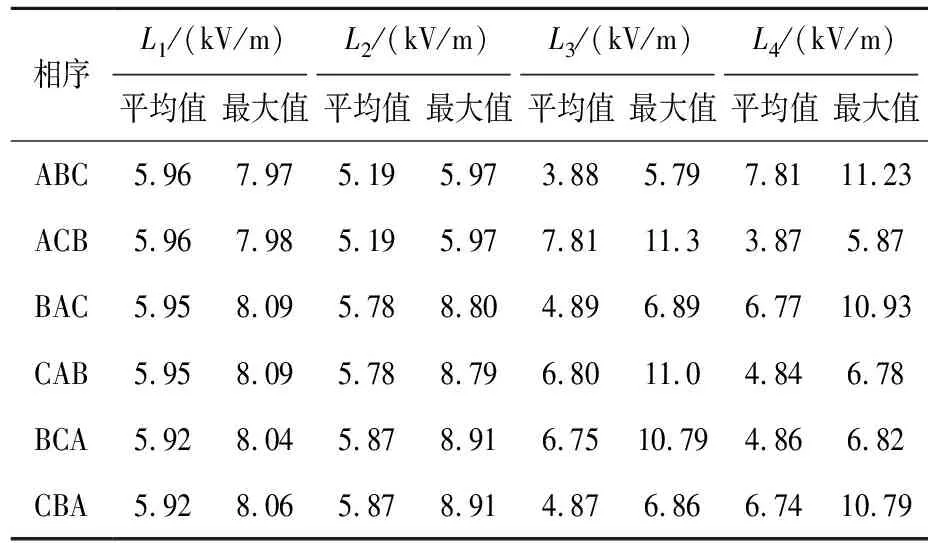
表4 1 000 kV导线不同相序下电场强度平均值及最大值
表4中的量化结果与图5的结论一致,其中,整个平面内的电场强度最大值在各相序下分别为:11.23、11.26、10.93、10.97、10.79、10.79,说明在500 kV线路相序为abc时,1 000 kV线路相序为BCA或CBA时,下方电场强度最大值最低,相较于同序、逆序,降低了4.17%。
2.2.2 500 kV线路相序影响分析
保持1 000 kV线路相序为ABC及其他参数不变,改变500 kV的相序,分析不同相序(分别为abc、acb、bac、cab、bca、cba)情况下,4条观测线上电场强度的变化趋势,如图7所示。
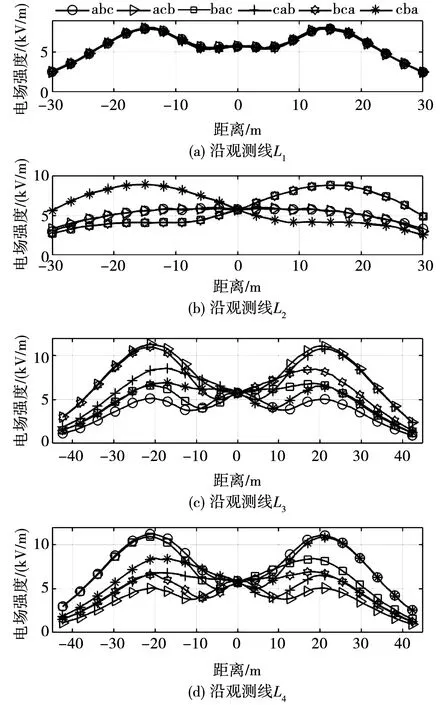
图7 500 kV线路不同相序下电场强度变化趋势
500 kV相序不同对下方电场强度的影响规律与1 000 kV相序大同小异,其表现结果虽然不同,但原理仍为同相导线交叉处的电场强度最高,因此分析过程此处不再赘述。
综上,线路相序对下方区域电场强度有明显影响,对称性也有所不同,但不改变其变化趋势、极值点位置等特性。1 000 kV与500 kV线路互为同序时,L3路径上的电场强度值最低,L4路径上的电场强度值最高;互为逆序排列时,L3的电场强度最大,L4电场强度最小;同序和逆序情况在L2路径上的电场强度均较低,相序对L1的电场强度无影响。另外证明了一个结论:同相导线交叉处的电场强度最高。
若从整个平面内的电场强度最大值来考虑,可以发现,在整个平面内(即综合4条观测线)的电场强度,同序排列时电场强度最大值约为11.23 kV/m,逆序排列的电场强度最大值也约为11.26 kV/m,而其他相序情况的电场强度最大值均为10.79~10.97 kV/m左右。因此,要降低下方区域的电场强度最大值,则排除同序和逆序排列情况,选择其他相序排列,但减小幅度不大。
2.3 交叉角度影响分析
保持其他参数不变,改变1 000 kV导线与500 kV导线的交叉角度,分析不同交叉角度(分别为30°、45°、60°、90°)情况下,4条观测线上电场强度的变化趋势,如图8所示。可以看出,双方导线交叉角度对线下区域各路径上的电场强度大小有一定影响,但不影响电场强度变化趋势,也不改变其对称性,虽然极值点位置随着交叉角减小而往外移动,但实际上其仍位于导线交叉点处。由于交叉角变化,导线之间的几何关系发生变化,导致交叉点与中心点的距离发生变化,所以交叉点才随着交叉角的减小而远离中心点,即极值点仍位于导线交叉点附近。
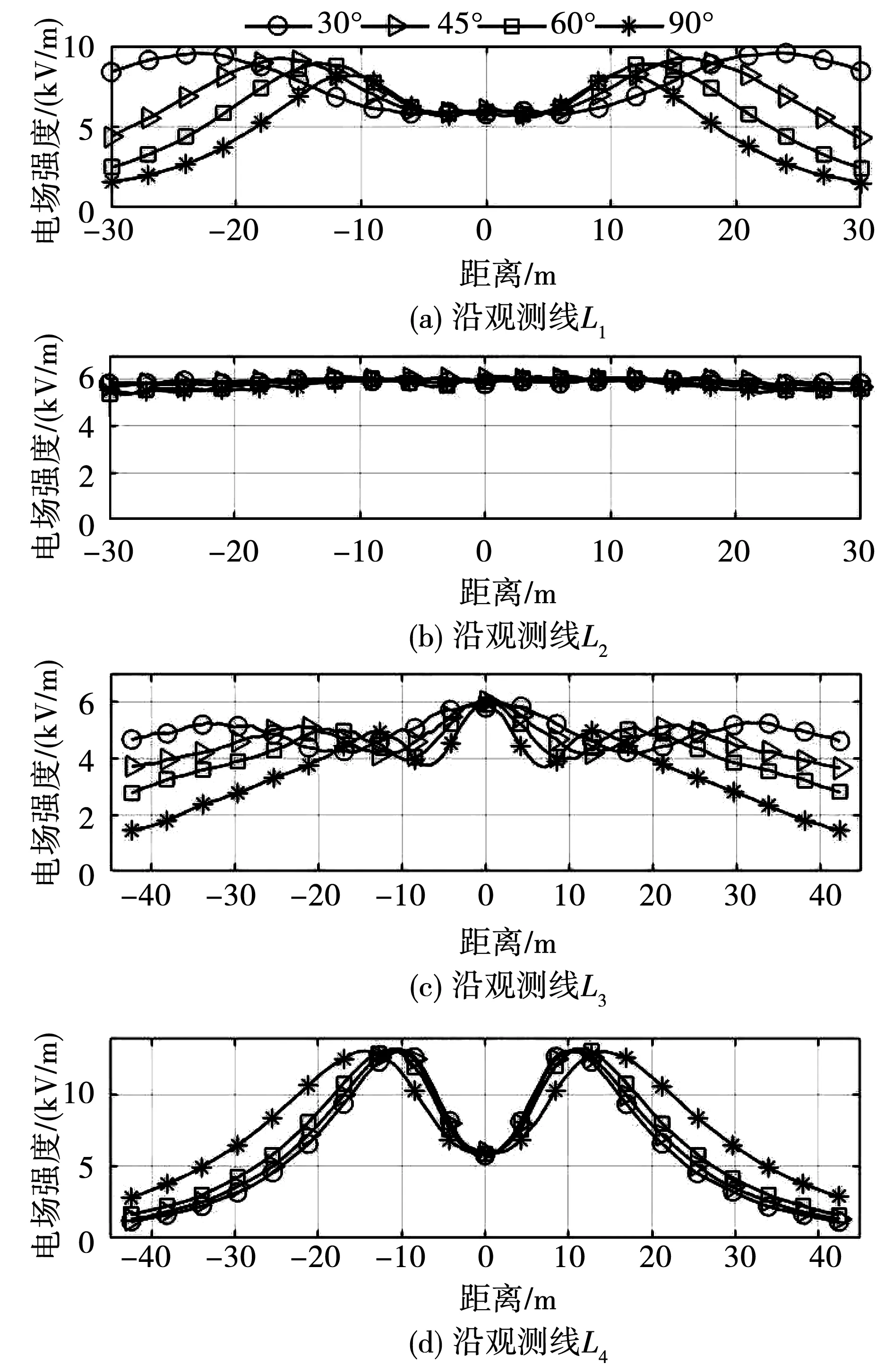
图8 不同交叉角度下电场强度变化趋势
随着交叉角度增大,L1路径上的电场强度整体及最大值均有明显下降;L2路径上的电场强度受影响极小;L3路径上的电场强度整体有明显下降,但最大值不变;L4路径上的电场强度在交叉区域内有所减小,在交叉区域以外有所增大,且最大值不变。
量化得到不同交叉角度下4条观测线上电场强度的平均值及最大值,如表5所示,单位:kV/m。
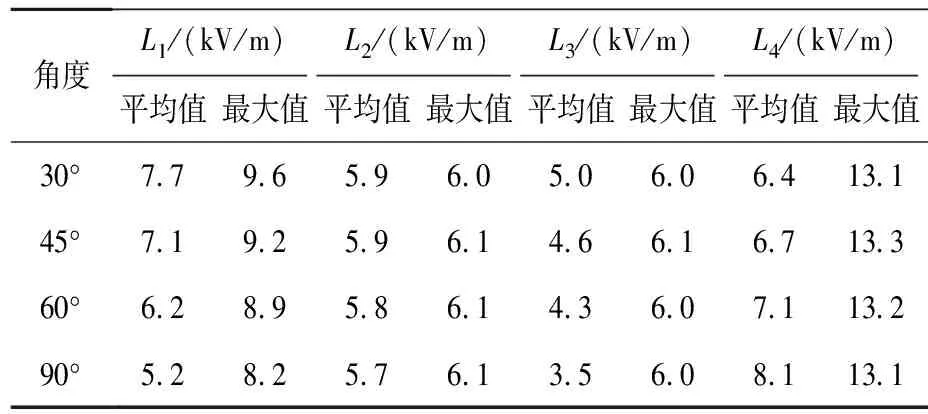
表5 不同交叉角度下电场强度平均值及最大值
由表5可知,随着交叉角度由30°增大到90°,L1沿线电场强度平均值及最大值有明显减小,减小幅度分别为31.89%、14.83%;L2沿线电场强度平均值及最大值几乎不受影响,波动范围不超过0.2 kV/m;L3沿线电场强度平均值减小了28.38%,但最大值却基本不变;L4沿线电场强度平均值增大了26.53%,但最大值却基本不变。
综上,交叉角度对线下区域近地面1.5 m空间的电场强度最大值几乎没有影响,但随着交叉角度增大,电场强度平均水平有明显下降。因此,选择90°交叉跨越角可改善交叉跨越区域下方区域的电场分布。
2.4 相位差影响分析
保持其他参数不变,改变1 000 kV线路与500 kV线路的相位差,分析不同相位差(分别为-60°、-30°、0°、30°、60°)情况下,4条观测线上电场强度的变化趋势,如图9所示。
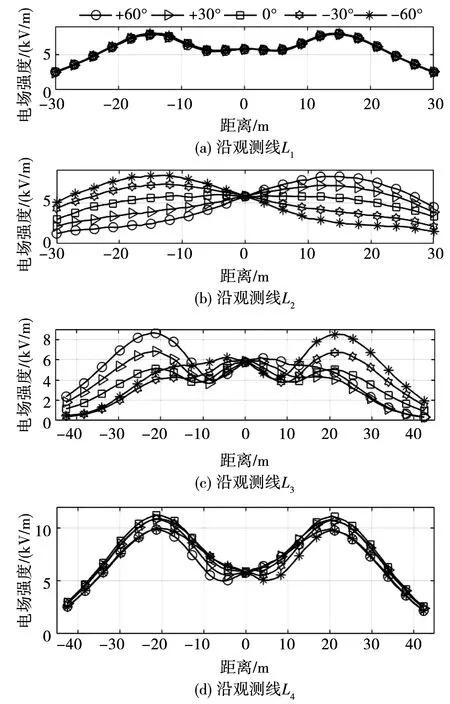
图9 不同相位差下电场强度变化趋势
由图9可知,跨越双方线路的相位差对下方区域电场强度大小有明显影响,但不改变其变化趋势、对称性、极值点位置等特性。其中相位差对L1观测线上的电场强度几乎没有影响;L2观测线上,左半边电场强度随着相位差增大而减小,右半边反之;L3观测线上,电场强度整体及其最大值均随相位差增大而增大;L4观测线上,电场强度整体及其最大值均随相位差增大而减小。
量化得到不同相位差下4条观测线上电场强度的平均值及最大值,如表6所示,单位:kV/m。
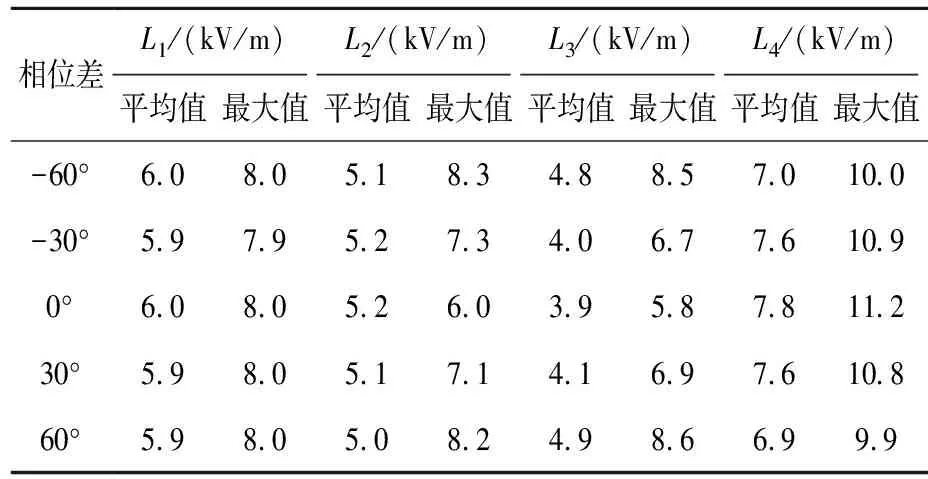
表6 不同相位差下电场强度平均值及最大值
由表6可得,当相位差由0°增大到±60°时,L1沿线电场强度的平均值及最大值均不变;L2沿线电场强度的平均值波动幅度也不超过0.22 kV/m,但最大值却增大了43.77%;L3沿线电场强度的平均值及最大值分别增大25.19%、49.35%;而L4沿线电场强度的平均值及最大值分别减小11.07%、11.95%。
由于观测线L4上电场强度整体均高于其他路径,因此观察L4路径上电场强度受相位差的影响规律可以发现,选择±60°的相位差可降低下方1.5 m平面内的电场强度最大值。
2.5 排列方式影响分析
保持其他参数不变,改变1 000 kV线路与500 kV线路的排列方式(主要研究正三角和水平排列方式;另外,改变排列方式时,需保持线路的几何中心高度不变,而非单纯改变中间相导线的高度),分析双方线路不同组合的排列方式(分别为正三角-水平、正三角-正三角、水平-水平、水平-正三角,其中前者为1 000 kV线路,后者为500 kV线路)情况下,4条观测线上电场强度的变化趋势如图10 所示。
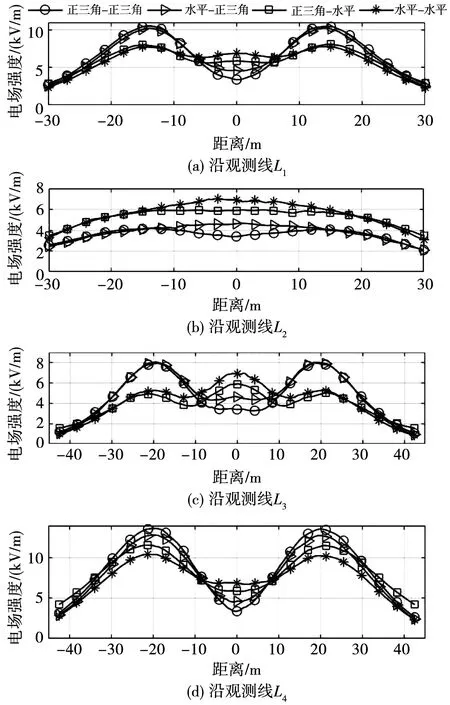
图10 不同排列方式组合下电场强度变化趋势
从图10可以发现,跨越双方线路的排列方式对下方区域电场强度大小有明显影响,但不改变其变化趋势、对称性、极值点位置等特性。其中,L1观测线上正三角-正三角与水平-正三角排列时的电场强度最大值均大于正三角-水平与水平-水平排列,且水平-正三角略小于正三角-正三角,水平-水平略小于正三角-水平;L2观测线上的情况与L1相反,L3、L4观测线上的情况与L1大体一致。
量化得到不同排列方式组合下4条观测线上电场强度的平均值及最大值,如表7所示,单位:kV/m。
表7所得量化结果与图10结论一致,且整个1.5 m平面内电场强度最大值位于L4路径上,而水平-水平组合下的电场强度最大值相较于正三角-正三角组合降低了23.51%。
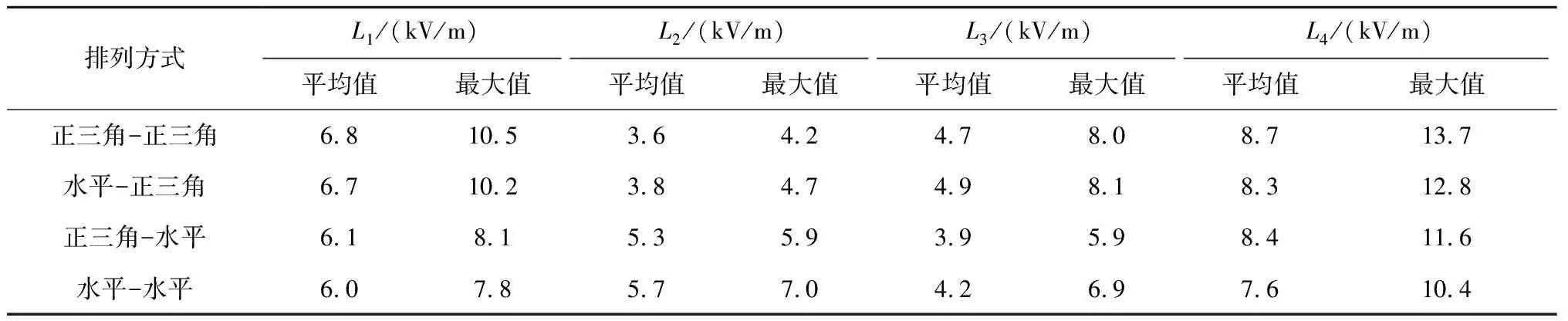
表7 不同排列方式下电场强度平均值及最大值
综上,就该平面内的电场强度最大值而言,即观察L4路径上的电场强度变化趋势,发现电场强度最大值存在以下关系:水平-水平<正三角-水平<水平-正三角<正三角-正三角,说明水平排列能够有效降低交叉跨越区域下方电场强度最大值,因此交叉跨越双方线路可尽量选择水平排列方式,能够起到降低下方区域电场强度最大值的效果。
3 交跨线路感应电压影响因素分析
除了考虑交叉跨越区域的空间电场,还需考虑线路间的电磁耦合问题,研究交跨线路在相邻线路产生的感应电压。以下方500 kV线路停运为例,分析上方1 000 kV线路对其产生的感应电压在不同相序、跨越高度、交叉角下的变化情况。
3.1 交跨线路感应电压理论计算
为了计算交叉跨越区域下方线路上的感应电 压,需要采取微分化思想[18],将线路分成若干个小段,当分段足够多时,即可近似看做每小段与上方线路呈平行状态,则可根据感应电压一般公式[19]计算得到每小段的感应电压,然后进行叠加计算,可得到线路总的感应电压。
静电场中感应电压可表示为
(8)
由于微分化,则式(8)可化为
φ=El。
(9)
式中:φ为下方线路每一小段上的感应电压;E为每小段的电场强度均值;l为每小段的长度。
3.2 交跨线路感应电压影响因素分析
3.2.1 相序影响分析
改变上方线路的相序,按照上述理论,得到不同相序排列时下方线路abc三相导线的感应电压,如图11所示。可以看出,随着上方线路相序变化,下方线路的感应电压变化极小,最大变化率不超过3.6%;中间相的感应电压均小于边相,且边相感应电压相等,这是由三相导线的相对位置决定的。

图11 不同相序时下方线路感应电压变化图
3.2.2 跨越高度差影响分析
改变双方线路的高度差,得到不同高度差时下方线路abc三相导线的感应电压,如图12所示。可以看出,随着跨越高度差增大,下方线路的感应电压大幅度减小,说明高度差对感应电压起主要作用。因此要减小感应电压,可提高双方线路的高度差。
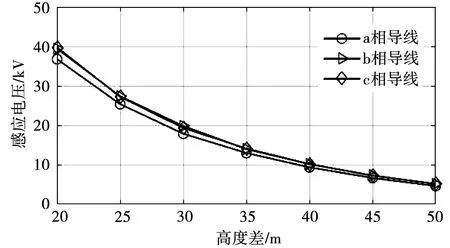
图12 不同高度差时下方线路感应电压变化图
3.2.3 交叉角度影响分析
改变双方线路的交叉角度,得到不同交叉角时下方线路abc三相导线的感应电压,如图13所示。可以看出,当交叉角从90°减小到30°时,感应电压无明显变化;当交叉角降到30°以下时,中间相感应电压明显减小,而边相感应电压明显增大。因此为防止感应电压过高造成危害,应尽量使交叉角度大于30°。
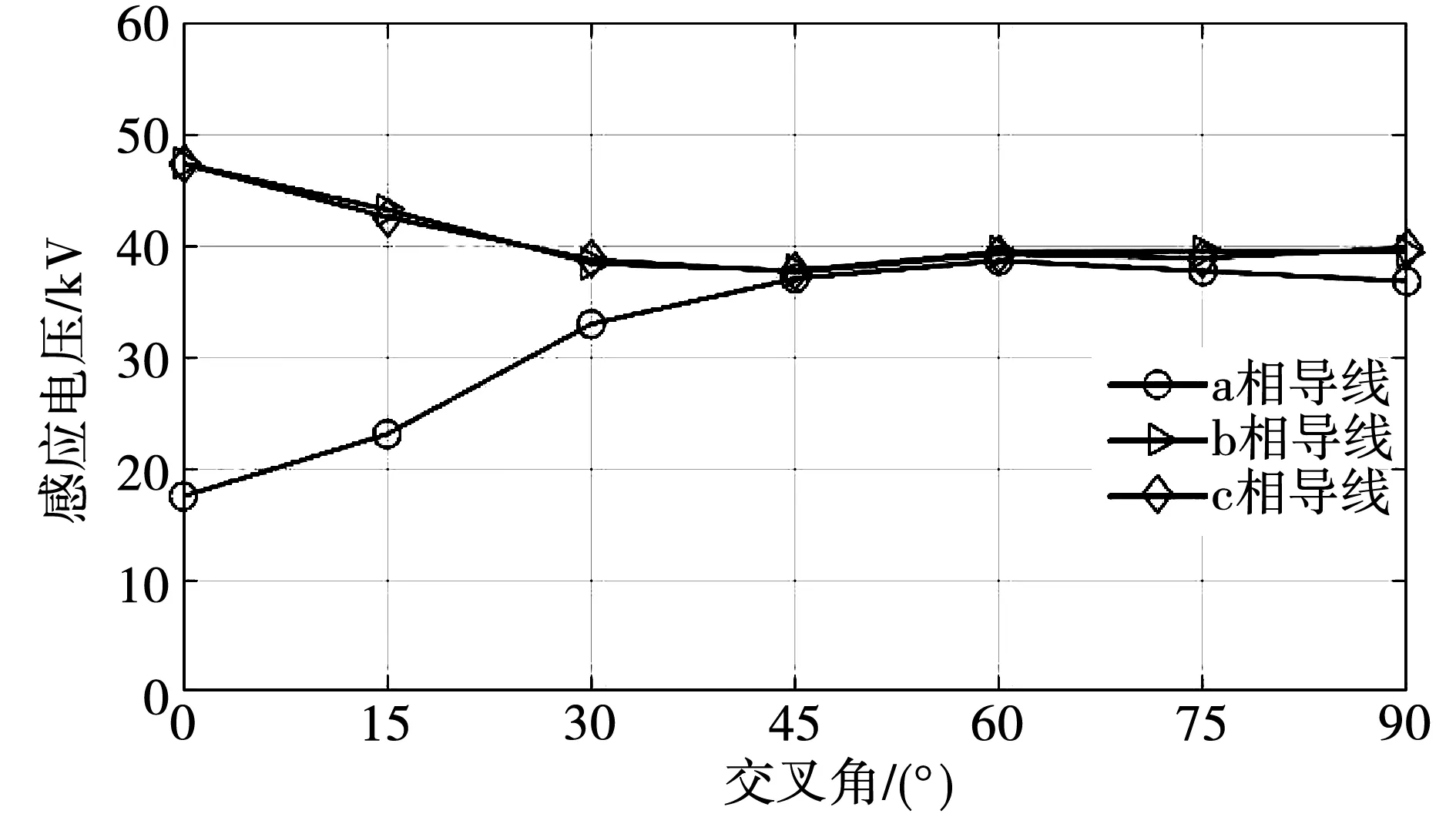
图13 不同交叉角时下方线路感应电压变化图
综上,交叉跨越区域下方线路的感应电压受相序影响不大;高度差与感应电压成反比,且对感应电压起主导作用;交叉角在30°以上时对感应电压无影响,小于30°时会增大感应电压最大值。
4 电场强度仿真与实测对比验证
由于实测数据有限,本文实测数据以500 kV交叉跨越220 kV线路为例,进行仿真与实测数据的对比,来验证本文的建模方法及理论分析的正确性。选取500 kV福燕Ⅰ路和220 kV东高Ⅱ路成90°交叉跨越区域进行空间电场实测,如图14所示。在交叉跨越处,500 kV福燕Ⅰ路B相离地高度为25.5 m;220 kV东高Ⅱ路A相离地高度为11.5 m。

图14 福燕Ⅰ路与东高Ⅱ路交叉跨越区域实测图
测试点选取D1~D11共11个测点(如图15所示),测点间距5 m,起始测点D1距离双方线路边相导线均为5 m,测量路径与水平方向成45°,共测量4个高度(即10、15、20、25 m)下沿着D1到D11方向的电场强度。

图15 交叉跨越区域测点示意图
按照实际线路的参数并利用Ansys软件建立等比例的交叉跨越区域三维仿真模型,并仿真得出以上测点的电场强度数据,与实测数据对比,如图16所示。可以看出,500 kV福燕Ⅰ路和220 kV东高Ⅱ路交叉跨越区域中,沿着实测路径,电场强度的仿真值和实测值的变化趋势及大小都是相近的,4个高度下的实测值和仿真值之间的最大相对偏差不超过12%,在误差允许范围内。
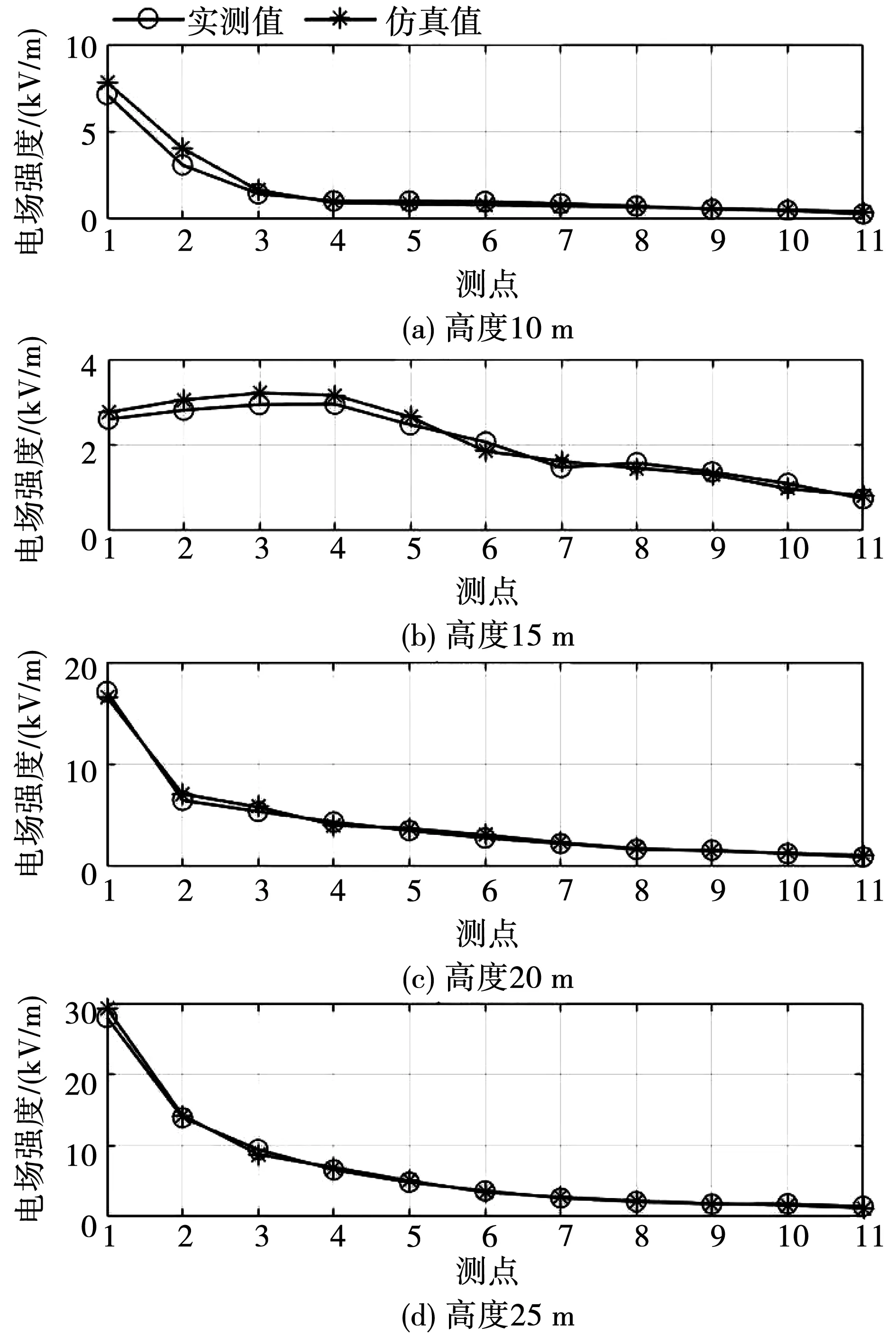
图16 交叉跨越区域仿真与实测数据对比图
综上所述,本文对于高压输电线路交叉跨越区域采用的建模仿真方法及理论分析方法所得到的结果与实测数据是吻合的,验证了本文方法的正确性、合理性及可行性。
5 结 论
相较于现有文献,本文设置4条观测线(涵盖整个离地1.5 m空间)分析各个因素对线下区域电场强度的影响规律,一方面,本文分析结果是对比整个空间内的电场强度而得出的,而不是仅研究一条观测线的结果,因此结论更具有可信度和说服力;另一方面,本文研究的影响因素更为全面,包括导线高度、相序、交叉角度、相位差及排列方式,因此结论更完善。
综合上述分析发现,导线高度、相序、交叉角度、相位差及排列方式等因素对高压输电线路交叉跨越区域下方离地1.5 m高度内的电场强度有明显影响:
1)1 000 kV导线由25 m升高到37 m,线下电场强度最大值降低20.72%;500 kV导线由25 m升高到37 m,线下电场强度最大值降低63.95%,可见随着导线高度增大,线下电场强度最大值明显减小,其中下方导线高度影响更大。
2)相序改变,下方区域电场强度分布也随之改变,但电场强度最大值变化不大,最大仅降低4.17%;且交叉跨越区域下方电场强度最大值出现在同相导线交叉处。
3)随着交叉角度增大,下方电场强度分布有所变化,平均电场强度随交叉角度增大而减小,电场强度最大值保持不变,因此选择90°交叉跨越可改善下方电场分布。
4)改变相位差,下方电场强度分布也随之变化,当相位差为±60°时,电场强度最大值下降约11.95%。
5)水平排列方式下线下区域电场强度最大值明显减小,水平-水平组合下的电场强度最大值相较于正三角-正三角组合降低了23.51%。
此外,高度差与交叉跨越区域下方线路的感应电压成反比,且对感应电压起主导作用;相序对感应电压影响不大;交叉角在30°以上时对感应电压无影响,小于30°时会增大其最大值。
因此,为减小线下电场强度最大值或改善线下电场强度平均水平,在经济条件允许的情况下提高交叉跨越双方导线高度,特别是提高下方导线高度可取得更好的效果。此外,采取垂直交叉跨越、±60°相位差或水平排列方式等均可降低下方电场强度最大值且具有成本投入小的优点,但效果没有提高导线高度措施好。为防止交叉跨越区域相邻线路感应电压过大而造成危害,可适当提高双方线路的跨越高度差,或使交叉角度保持在30°以上。
