交比及性质的初等证明与应用*

华南师范大学附属中学(510630) 罗碎海 袁宇飞

只有认识了圆锥曲线的极点与极线性质以及点列与线束交比的射影性质,才能深刻认识圆锥曲线的数学本质.有些高考题就是这些问题的特殊化,可一望而知答案.笔者最近重做2013年江西省的高考题,自觉趣味更浓,发现文理题同源于交比.查阅资料,有多篇文章探讨推广[1,2,3],但觉还需再迈一步,洞悉本质.现拙笔写出,与同行交流.试看考题新分析:

例1(2013年江西高考理数20题)如图,椭圆C:=1(a＞b＞0)经过点离心率直线l的方程为x=4.

(1)求椭圆C的方程;

(2)AB是经过右焦点F的任一弦(不经过点P),设直线AB与直线l相交于点M,记PA,PB,PM的斜率分别为k1,k2,k3.问:是否存在常数λ,使得k1+k2=λk3?若存在,求λ的值;若不存在,说明理由.

分析(1)易得椭圆C的方程为=1.

(2)应用圆锥曲线射影性质分析如下:由(1)可得椭圆右焦点F(1,0).已知的直线l方程为x=4,正是椭圆焦点F关于椭圆的极线(即准线),而且直线PF⊥x轴.由椭圆的交比性质可知直线束PA,PB,PF,PM是一组调和线束,由于直线PF斜率不存在,则由调和线束与斜率关系有=−1,化简即k1+k2=2k3,即λ=2.(文末详细再说理由)

若学生能掌握这些知识,可快速得到了答案,解题就只需用高中知识书写表演而已了.

高等几何中的交比与调和比以及圆锥曲线的射影性质,完全可以用高中数学知识证明.为了使高中学生更本质的认识圆锥曲线,我们有必要做高等数学初等化的工作.

1 交比的定义与性质

1.1 点列中四点的交比

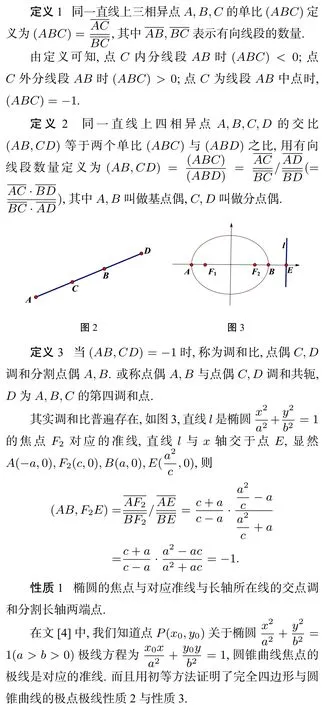
性质2过点P作两条直线分别与圆锥曲线交于A1,B1与A2,B2,若A1A2∩B1B2=D,A1B2∩A2B1=C,连CD交A1B1于R,交A2B2于S,则P,R调和分割A1,B1,P,S调和分割A2,B2,且R,S调和分割C,D.

原文中此性质的证明与圆锥曲线无关,它是完全四边形的性质.由于调和分割,当四边形放在圆锥曲线内时,极点与极线的关系就呈现出来.得到完全四边形的性质.

图4

性质3一个四边形的四个顶点在一条二次曲线上,则这个四边形的对边延长线的交点(假设四边形对边不平行)及其对角线交点的组成的三角形的任一顶点是其对边的极点.

如图5,点Q的极线是直线PR,点P的极线是直线QR,点R的极线是PQ.另外点P,R调和分割S,T;点Q,S调和分割C,A;点Q,R调和分割U,V;由文[4]中性质4还可知,点P,R调和分割M,N,等等.

图5

1.2 线束的交比

定义4线束中的四直线li(i=1,2,3,4),则

叫做l1,l2,l3,l4的交比,其中l1,l2,叫基线偶,l3,l4叫分线偶.其中(l1,l2)表示l1到l2的角,是有向的.

性质4设线束S的四直线a,b,c,d被直线s截得A,B,C,D,则(AB,CD)=(ab,cd),即四点的交比与四线的交比相等.

分析如图6,过点S作直线s的垂线,垂足设为H,则三角形ASC面积=·AC·SH,根据正弦定理,三角形ASC的面积还可以用SA·SC·sin∠ASC表示,这样,sin∠ASC=(AC·SH)/(SA·SC);这样把上面等式中的正弦全部换成这样的表达式,立即就得证了(AB,CD)=(ab,cd).

图6

由性质4可得

性质5如果两条直线截同一线束,则所得对应四点的交比相等.如图7,(AB,CD)=(A′B′,C′D′).

图7

性质6两个线束投射同一点列,则得对应四直线的交比相等.如图8,有(ab,cd)=(a′b′,c′d′).

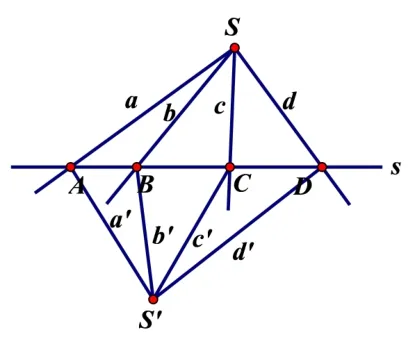
图8

定义5如果四直线li(i=1,2,3,4),满足(l1l2,l3l4)=−1,称线偶l3,l4和线偶l1,l2调和分离(调和共轭),也称l4为第四调和线,交比值−1称调和比.

特殊:三角形一个角的内外角平分线调和分离这个角的两边.

进一步我们得到交比与直线斜率的计算公式.

图9

进一步可得到直线系的两性质:

图10

2 2013年高考江西数学文理20题分析

用以上知识,发现2013年高考江西数学文理20题同源于交比,只是理科比文科题多了一步调和比不变性的射影变换,现详细说明两题的联系与本质.

例1(2013年江西高考理数20题)题干在文首.

详细分析:(1)易得椭圆C的方程为=1.

(2)如图11,由(1)可得椭圆右焦点F(1,0).已知的直线l的方程为x=4,l正是点F关于椭圆的极线MN(也是准线).设MN与x轴的交点是D,椭圆长轴两端点为A1,A2,则由性质1知(A1A2,FD)=−1.

图1

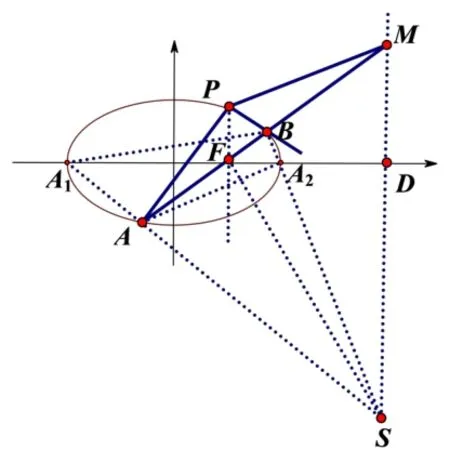
图11

连A1B,AA2,则A1AA2B是椭圆内接四边形,其对角线交点是F.由性质3知A1A与BA2两线相交,设交点为S必在F的极线MN上.连FS,由性质4与性质10可知线束SA1,SA2,SF,SD调和分割.由于该线束又与直线AM交于A,F,B,M四点,由性质5知(AB,FM)=−1.由性质6知过A,F,B,M的四线PA,PB,PF,PM为一组调和线束.

(1)求椭圆C的方程;

(2)如图,A,B,D是椭圆C的顶点,P是椭圆C上除顶点外的任意一点,直线DP交x轴于点N,直线AD交BP于点M.设BP的斜率为k,MN的斜率为m.证明:2m−k为定值.

图12

分析(1)由已知易得椭圆方程为+y2=1.

(2)由于ABPD是椭圆内接四边形,点M与N分别是四边形对边AD与BP,AB与DP交点.连四边形对角线AP与BD,设交点为E(如图13).则由性质3知ME为点N关于椭圆的极线,点N在x轴上,则极线ME⊥x轴.由性质10可知,线束MA,MB,ME,MN是一组调和线束,斜率分别为即为定值.

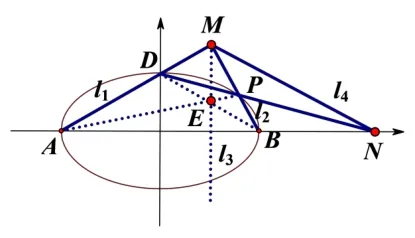
图13

搞清了题目的源头与发展变化,看到了理科题是比文科题多设计了一步射影变换(性质6).进一步从椭圆退到圆或向其它圆锥曲线(双曲线、抛物线)推广,从理科题向竞赛题推广就成了很简单的事情了.