多维度比较“反比例函数”习题——以人教版和东京版为例

云南省昆明市云南师范大学(650500) 杨 壮 杨亚平

1 研究背景

教材是教学内容的重要载体,也是教师沟通学生、学生学习的载体.近些年,数学教材对比一直是研究热点,数学教材由正文、例题和习题组成,习题作为数学教材的重要组成部分,在数学教材中发挥着重要作用,在一定程度上反映了数学教材的特征和数学教材编写者的设计意图[1].

反比例函数是初中阶段“数与代数”的重要模块之一,是学习函数知识的基础,作为中考数学的热点命题方向,这部分内容题源丰富,题目既源自于教材而又高于教材,因此选择反比例函数作为研究的主题.因为日本的学生在国际测试中的优异表现以及中日两国相似的文化背景,在一定程度上日本的教育改革经验能给我国带来一定的影响,故研究中日两国的数学教材有重要意义.

2 研究设计

2.1 研究对象

本研究选取人教版课标教材九年级下册“第二十六章”、东京版《新编(新)数学·1》“第四章”的部分习题为研究对象.习题是教材的重要组成部分,是学生学习过程中必不可少的重要环节,一方面有助于学生加深对数学知识的理解,形成良好的数感与数学思维,另一方面也有助于学生获得必要的技能,为后续学习和解决问题奠定基础,提供支持.基于此,本研究从节中、节末、章末三个位置进行整理习题,针对人教版中“练习”“习题”“复习题”进行统计和考量;同理,东京版中研究“确认题、问、补充的问题”“基本的问题”“章的问题A、B”等板块习题.

2.2 研究方法

根据人教版与东京版反比例函数习题的呈现,本研究运用比较研究法和文献研究法,从习题数量、数学核心素养、数学思想方法、数学文化以及综合难度5个维度习题进行比较研究研究.其中习题的数学文化按照习题的内容分布,从数学史、数学与现实生活、数学与科学技术、数学与人文艺术4方面对两版教材的习题进行数学文化比较.习题的综合难度将结合鲍建生教授的综合难度模型[2]与覃淋的统计习题难度测量模型[3],从认知、背景、运算、知识量、与例题的关联程度5个难度因素对两版教材的习题进行难度对比.

3 研究结果

3.1 习题数量比较

本研究采用的习题数量统计方法:若一道习题按(1)(2)(3)……编号,则按习题中的小题个数进行统计;若一个题目包含多个问题,但未分成(1)(2)(3)……,则按照一个题目进行统计.需要注意的是,东京版的反比例函数与正比例函数为同一章节的内容,部分习题混合在一起,需要人工进行辨别.基于以上统计方法,绘制两版教材中反比例函数部分的习题数量对比统计图,如图1所示.

图1

从习题数量上看,人教版习题总数为70,东京版习题总数为47,差异较大.人教版教材关注节中、节末、章末的习题,而东京版教材尤其关注节中的习题,重视教学过程中的练习.

3.2 习题数学核心素养比较

本部分通过分析教材习题体现的六大数学核心素养对人教版与东京版教材反比例函数习题进行统计分析,因反比例函数内容不涉及数据分析素养,故本部分仅从数学运算、数学建模、逻辑推理、直观想象、数学抽象这五大素养进行统计分析.统计方法为:分别统计人教版和东京版教材中考察各素养的“反比例函数”习题题目个数,并统计其在相应版本习题中所占比重.(如果一道习题涉及多个数学核心素养,则按多个数学核心素养统计)两版教材反比例函数习题在各素养类型上的统计结果如图2所示.

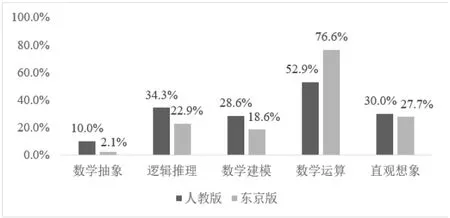
图2

1.数学运算和数学抽象素养呈两极分布

横向对比发现:两版教材“反比例函数”内容的习题在数学运算素养占比最高;往后依次为逻辑推理、直观想象和数学建模素养;从上图可发现,数学抽象素养在人教版和东京版教材反比例习题中都少有考察,仅占10%和2.1%.

2.两版教材习题侧重的素养类型基本一致

纵向对比发现各素养占比发现:人教版和东京版教材各素养占比按从大到小顺序排列均为数学运算＞逻辑推理＞直观想象＞数学建模＞数学抽象.

3.3 习题数学思想方法比较

数学思想方法是数学的精髓,是数学的本质所在[4].本部分主要关注数学思想方法在习题中的渗透,整理发现“反比例函数”的习题主要涉及数形结合、函数与方程、分类讨论这三种数学思想方法,从上述三个数学思想方法对两版教材的习题进行统计分析,统计方法为:分别统计人教版和东京版教材“反比例函数”中涉及以上三种数学思想方法的习题数,再除以本习题总数.(同一道习题可能涉及多个数学思想方法,规定只按最主要的数学思想方法进行计数统计.)两版教材反比例函数习题在数学思想方法上的统计结果,统计结果如表1所示.

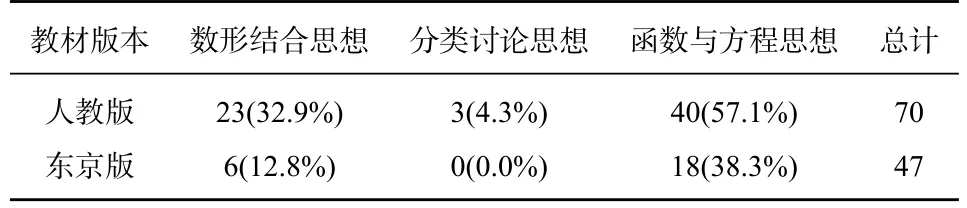
表1 反比例函数习题数学思想方法上的数量百分比

1.函数与方程思想与分类讨论思想呈两极分布

横向对比发现:两版教材的反比例函数习题在函数与方程思想所占百分比均为最高,人教版教材在函数与方程思想的百分比高达57.1%,由于反比例函数本身的特性,致使涉及函数与方程思想方法的习题数量最多;其次是数形结合思想和分类讨论思想;从上表可观察,分类讨论思想在人教版和东京版教材反比例函数习题中都少有甚至没有考察,人教版教材仅占4.3%,而东京版教材未涉及分类讨论思想.

2.两版本教材习题侧重的数学思想方法基本一致

纵向对比发现各数学思想方法占比发现:人教版和东京版教材涉及的数学思想方法占比按从大到小顺序排列均为函数与方程思想＞数形结合思想＞分类讨论思想.

3.4 习题数学文化比较

中国和日本有着相似的文化背景,加上数学文化博大精深,本部分志在比较两个版本教材习题在数学文化的异同.从数学史、数学与现实生活、数学与科学技术、数学与人文艺术四个方面对两版教材的反比例函数习题进行统计分析[5],统计方法为:分别统计人教版和东京版教材“反比例函数”习题在各个数学文化的习题数,再除以本习题总数得出相应的百分比,统计结果如表2所示.

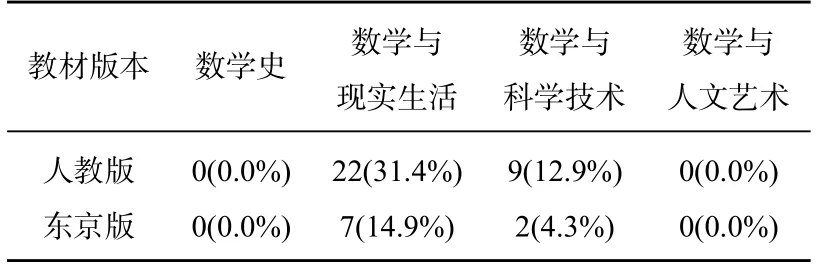
表2 反比例函数习题数学文化内容分布

1.数学与现实生活、数学与科学技术齐头并进

横向对比发现:两版教材反比例函数习题涉及数学文化的占比不到一半,也即只有不到一半的习题涉及了数学文化,其中数学与现实生活占比最高,其次为数学与科学技术;从图表可发现,数学史、数学与人文艺术在人教版和东京版教材反比例函数习题中均未涉及.

2.两版本教材习题侧重的数学文化基本一致

纵向对比发现各数学文化占比发现:人教版和东京版教材涉及的数学文化占比按从大到小顺序排列均为数学与现实生活＞数学与科学技术＞数学史=数学与人文艺术.

3.5 习题综合难度比较

本文参考了鲍建生教授的综合难度模型与覃淋在《“中国大陆”“日本”和“中国台湾”高中数学教材统计习题难度比较研究》中提出的统计习题难度测量模型,并且结合反比例函数的要求及反比例函数习题的特征,构建了一个五因素习题难度测量模型,各难度因素的及在三水平的划分如下.

认知(A)——A1:记忆,即可以直接回忆反比例函数的相关知识就能解决的问题;A2:理解,即在理解反比例函数知识的基础上,需要通过组织前后所学知识才能解决的问题;A3:探究,如解决反比函数问题的存在性问题等.

背景(B)——B1:无背景,即反比例函数习题为纯数学背景;B2:个人生活,即反比例函数的习题与学生的生活相关联,关注与个体自身、个体所在家庭、个体同伴等相关的日常活动;B3:公共常识,即反比例函数习题的背景为大众所熟知.

运算(C)——C1:无运算,即没有运算步骤的反比例函数习题;C2:数值运算,即只含常数的数学题;C3:符号运算,即反比例函数的习题需要用到符号表示数字的习题.

知识量(D)——D1:一个知识点;D2:两个知识点;D3:三个及三个以上知识点.

与例题的关联程度(E)——E1:高度相关,即反比例函数的习题与教材的例题部分基本一样;E2:一般相关,即反比例函数的习题与教材的例题部分相似;E3:无关,即跟教材的例题一点都不同,需要从其它角度思考.

各难度因素加权平均计算方法:例如对于难度因素“背景”,第1个水平“无背景”的习题数有15道,第2个水平“个人生活”的习题数有9道,第3个水平“公共常识”的习题数有13道,则“背景”因素的加权平均为=1.95.

因两版教材反比例函数习题总量相差较大,仅用题目数量无法清晰看出具体情况,故选择各难度因素各水平占比来直观地比较,如图3所示.为了进一步考察两版本教材的综合难度水平.通过对两版本教材中五个难度因素的不同水平题目的统计,并利用加权平均计算公式得到五个难度因素的加权平均值,绘制出反映两版本教材综合难度的雷达图模型,如图4所示.

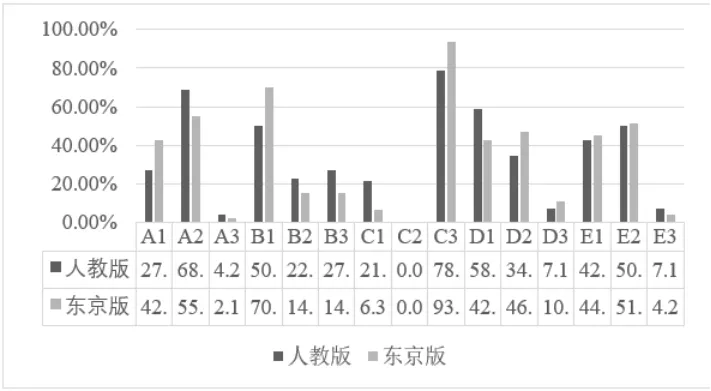
图3

图4

从认知因素分析,记忆水平层面上人教版的考察少于东京版,而理解水平层面上的考察高于东京版,两版教材均较少考察探究水平,人教版教材的认知因素综合难度略高于东京版.

从背景因素分析,两版教材均设置无背景、个人生活、公共常识的习题,但东京版教材主要考察无背景的习题,人教版教材的背景因素综合难度略高于东京版.

从运算因素分析,两版教材主要考察符号运算,并且均未设置数值运算的习题,较少考察无运算的习题,东京版,人教版教材的运算因素综合难度低于东京版.

从知识量因素分析,两版本教材习题主要涉及一到两个知识点,较少设置包含三个及三个以上知识点的习题,人教版教材的知识量因素综合难度大致与东京版相同.

从与例题的关联程度因素分析,两版本教材反比例函数习题分布基本一致,均主要考察与例题相关的习题,但与例题无关的习题上东京版教材高于人教版,人教版教材的与例题关联程度因素综合难度高于东京版.

综上,人教版教材的习题综合难度略高于东京版.

4 启示

4.1 习题设置应遵循创新性与激励性

反比例函数习题涉及的数学思想方法和数学文化都较为局限,题型陈旧,大部分习题无背景,缺乏创新性与激励性,可能致使学生对数学学习缺乏兴趣.《义务教育数学课程标准(2011版)》明确提出要发展学生的创新意识,习题是教材的重要组成部分,承担着发展学生关键能力的重要作用,因此教材习题的编写要紧扣课标,遵循激励性与创新性,注意与数学史、人文艺术相关联,增加学生的学习兴趣,加深对数学知识的理解,让学生感悟数学之美.

4.2 习题编写应注重导向性和综合性

反比例函数属于数与代数模块,习题蕴含的核心素养在数学运算、逻辑推理、直观想象较数学抽象更多,函数知识本身就较难理解,较为抽象,但两版教材过于压缩数学抽象的考察,缺乏对学生抽象意识的导向性培养,对六大核心素养考察不够全面.习题的编写既要符合课标要求,也要注意习题蕴含的数学核心素养的综合性与导向性.