单元整体教学促进深度学习发生
——“全等三角形”单元教学思考与实践
2022-07-14北京师范大学昌平附属学校102206秦虹柳
北京师范大学昌平附属学校(102206) 秦虹柳
任何知识都不是孤立的,都属于系统结构中的局部,整体观下的教学重视知识间的联系,关注知识的形成过程,有助于学生了解问题的本质,对学习内容形成系统化认知.本文记录的是笔者以学生的深度学习为追求,对“全等三角形”进行的单元教学思考与实践,在内容上,整合教材安排,突出体现知识的整体性和系统性;在组织形式上,通过设计开放性问题和活动,给学生充足空间,使学生经历完整思维过程;在目标导向上,以几何直观和空间观念为导向,以促进学生思维发展、实现深度学习为目标.
“全等三角形”在各版本教材中的安排大致相同,第一课时是全等三角形的概念和性质,之后的几个课时分别对全等三角形的不同判定方法进行教学,最后进行综合应用.由于三角形全等的关系与三角形的位置无关,所以,全等三角形的相对位置呈现多样性,从图形运动的角度理解全等三角形有助于辨识对应边和对应角.对于全等三角形的判定方法,学生需要具备综合运用多种判定方法解决问题的能力.因此,我整合教材安排,从单元整体教学的角度出发进行教学调整.第1课时:全等三角形的概念和性质,提升学生的识图能力,帮助学生从图形运动的角度理解全等三角形.第2课时:探索全等三角形的判定方法.第3课时:全等三角形判定方法的理解与运用.第4课时到第6课时:综合运用多种全等三角形的判定方法解决问题.本文重点对前3个课时的设计进行说明.
1 课时1——实践中感悟图形变换,发展空间观念
三角形仅发生位置变化时,与原三角形是全等的关系,对于两个全等的三角形,其中一个三角形可以看成由另一个三角形经过运动变换之后得到的,准确辨识全等三角形的对应边和对应角不仅需要借助几何直观,更需要从运动变换的角度理解图形,因此,在讲完全等三角形的概念和性质后,我设计两个开放性活动帮助学生发展空间观念.
活动1如图1所示,已知ΔABC,将它运动至新的位置,是否存在与它全等的三角形?如果存在,请说明ΔABC是怎样运动的,并找一找对应边、对应角.(每个学生手中有两个全等的三角形学具,学生可以借助手中的学具演示图形变化过程)

图1
学生首先需要借助图形的直观性进行初步判断,再借助手中的学具进行操作验证,在这个活动中,学生初步体会平移、旋转、翻折等图形运动过程,对认识几何图形的直观性以及从图形运动角度理解全等三角形有积极意义,由于整个活动充分放手,对学生具有一定挑战性,有助于学生经历完整的知识探究过程,学生的空间观念得到发展.
活动2借助手中两个全等的三角形学具,让一个ΔABC动起来,可以运动到任意位置,互相说一说ΔABC是怎样运动的.
这个开放性活动给学生充足空间,打开学生思维,激发学生的创造力,学生对平移、旋转、轴对称等图形运动过程有进一步认识;在复杂图形中辨识全等三角形对应边和对应角的能力得到提升;几何直观和空间观念得到进一步发展.
通过这样的两个活动,学生对全等三角形有较深刻的理解,虽然学生还没有系统学习图形变换的相关知识,但是,对几种基本图形变换已经有初步认识,这样的安排不仅有助于学生对全等三角形的理解,也为进一步学习图形变换相关知识做铺垫.
2 课时2——经历探究判定方法全过程,促进思维的严谨性
教材对全等三角形的判定方法是“分—总”的设计,教师应该带着自己的理解使用教材.全等三角形的几种判定方法是一个整体,学生应该经历探究判定方法的过程;在解决问题时,学生应该对几种判定方法有整体认知,经历分析问题、方法选择、解决问题的过程,因此,我对这部分知识进行了“总—总—分—总”的设计,本课体现第一个“总”,探究全等三角形的判定方法,下一课时体现第二个“总”,几种判定方法的综合理解与应用,然后的几个课时对几种方法进行巩固强化和综合应用.
本课中,我设计了探索全等三角形的判定方法的综合活动,虽然大多数学生知道应该探索更简单的方法判定三角形全等,但是学生的思维很凌乱,于是,我让学生按照自己的思路设计研究方案,只要有条理就可以.我预设了几种思路,(1)按照要素数量从少到多;(2)按照要素数量从多到少;(3)按照要素种类,比如先研究边,再加入角.
本课承载了提升学生思维能力的任务,如:在用六个要素可以判定三角形全等的前提下,需要探寻更为简单的方法进行判定,体现数学的简捷性;经历观察图形、分析图形、画图等过程,得出判定三角形全等的三个基本事实,体现了公理化思想和几何直观的重要意义;在探究全等三角形判定方法的过程中,涉及复杂的分类问题,体现数学的严谨性;通过证明“角角边”定理的过程,提升学生的几何推理能力.以下展示两种思路.
思路1按照要素从少到多的顺序如图2.

图2
在探究过程中,要按照一定顺序进行分类,在确定要素时,先确定数量,再确定种类,最后确定相对位置.要抓住变化因素和不变因素,不变因素是入手点.通过这个环节,学生对分类讨论的认识更加深入,学生的思维更加严谨,充分体会研究问题的逻辑性.值得注意的是,探究“三个要素”时,由于不是所有情况都能判定三角形全等,探究过程并没有结束,应该继续添加条件,直到能够判定三角形全等.在“三个角”确定的前提下,不能增加角的条件,增加一边后,满足“两角和一边”的条件,能够判定三角形全等,但是显然不够简捷.在“两边及一边对角”的基础上增加一边,满足“三条边”的条件;增加一角,满足“两角一边”的条件,都能判定三角形全等,但是不够简捷.显然,增加任何条件后都可以用更简单的方法判定全等,因此得出结论,判定三角形全等的方法有四种,分别是“两边及夹角”、“两角及夹边”、“两角及一角对边”、“三条边”对应相等的两个三角形全等.具体思路如图3:

图3
这样的设计体现了研究问题的完整思维过程,有助于学生整体把握知识框架,不仅重视结果,更重视知识的形成过程.探究过程培养学生的理性思维,提升学生的思维逻辑性和严谨性,对学生分类能力的培养有重要意义,有助于培养学生直观想象的核心素养.
思路2按照边、角分类思路.

图4
学生容易想到三条边对应相等的两个三角形全等,因此,判定三角形全等的条件从六个要素减少到三个要素,在此基础上,可以寻求更加简单的方法,先研究减少一边的情况,发现不能确定三角形时,要研究增加一角的情况.然后研究减少两边的情况,需要增加两个角的条件,最终探索出所有判定三角形全等的条件.
每个学生都有自己的思维特点,教师应该从学生的思维出发,不能以教师的想法为中心,而是顺应学生思维,培养学生思维的严谨性和考虑问题的全面性,在此过程中,学生探究问题的能力得到提升.
3 课时3——开放性活动提升学生分析问题、解决问题的综合能力
本课安排在探究全等三角形的判定方法之后,通过之前的学习,学生初步了解全等三角形的四种判定方法,本课以开放性问题和活动为载体,帮助学生深刻理解全等三角形的判定方法;提升学生在具体问题中分析条件,选择恰当的判定方法进行证明的意识和能力.
活动1如图5,已知ΔABM和ΔDCM全等,请写出适当的条件,可以依据以下不同的判定方法证明这两个三角形全等.

图5
(1)角边角:____.
(2)边角边:____.
(3)边边边:____.
(4)角角边:____.
通过这个开放性活动,帮助学生回顾全等三角形的四种判定方法,培养学生的识图能力,强调书写时的“对应”关系,同时,用“角边角”、“边角边”和“角角边”的方法进行判定时可以有多种添加方法,有助于提升学生的几何直观意识和推理能力.经历这个开放的学习过程,有助于学生整体把握全等三角形的判定方法,提升学生分析问题的能力,发展学生的逻辑推理能力.
活动2如图6,AC与DB交于O,图中有三对全等三角形,请你找一找,并选择其中的一对全等三角形,添加可以证明它们全等的条件.(添加条件尽量简单)

图6
全等三角形:____.
我的选择是:____.
添加条件:____.
当两个三角形具有特殊位置关系时,可能存在隐含的相等要素,比如常见的公共边、公共角、对顶角,抓住这些条件能够使问题简化.在利用“角角边”的方法判定全等时,要注意边可以是两对等角中任意一对等角的对边.
相对于活动1,这个活动对学生的思维能力要求更高,根据已知条件判定三角形全等时,要综合分析四种判定方法,充分利用已知条件并选择适当的方法进行判定.比如,对于ΔABO和ΔDCO,首先要拆解出图形,根据已知的一对对顶角相等,在分析四种判定方法后,可以依据“角边角”、“角角边”、“边角边”等方法添加条件.通过本活动,提升学生辨识复杂图形的能力,分析问题和解决问题的能力以及逻辑推理能力.
活动3如图7,已知OC平分∠AOB,P为OC上一点.

图7
问题1根据条件,你能想到什么?
问题2分别进行如下操作,你能想到什么?(三个图形分别出现)
(1)如图8,过点P向∠AOB两边作垂线,分别交OA、OB于M、N.

图8
(2)如图9,过点P作OC的垂线,分别交OA、OB于M、N.

图9
(3)如图10,点M、N分别在OA、OB边上,满足OM=ON.

图10
借助角平分线模型构造全等三角形,帮助学生学会分析已知条件,确定判定三角形全等的方法,分析思路如图11所示.由于需要构造图形,学生需要根据不同的判定方法进行思维的创造性活动,在学生思考问题的过程中,对全等三角形的几种判定方法有整体认识,对图形的理解也更加深刻,学生的分析问题、解决问题能力得到提升.

图11
活动4如图12,在ΔABC中,∠BAC的平分线AD交BC于D,你能添加一条辅助线,构造出全等三角形吗?如果能,请添加辅助线,并说明理由.
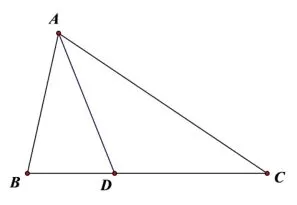
图12
本活动是活动3的延续,需要学生对全等三角形的判定方法进行整体把握,在观察图形特征和分析条件的基础上,需要依据不同的判定方法添加辅助线,并通过逻辑推理判定两三角形全等.在此过程中,学生需要经历完整的思维过程:分析已知条件确定判定方法确定相关条件加辅助线推理证明.由于判定方法不同,所以学生需要全面考虑问题,不断尝试,最终找到解决问题的方法.
由角平分线可得一对等角、一条公共边,在此基础上,需添加另一个相等的要素判定三角形全等,在AC边上截取AE等于AB,从而根据“边角边”定理判定ΔADE与ΔADB全等;作线段DE交AC于E,使∠4=∠3,根据“角边角”定理判定ΔABD和ΔAED全等;过点D向AB、AC边做垂线,但是需要两条辅助线,不符合条件;也能够想到由点D做AD的垂线,但是需要延长线段AB,也不符合条件;在AC上取一点E,使得∠AED=∠B,但是,在操作上存在困难.几种做法如下:
(1)如图13,在AC上截取AE=AB,根据“边角边”定理判定ΔABDΔAED.

图13
(2)如图14,作线段DE交AC于E,使∠4=∠3,根据“角边角”定理判定ΔABDΔAED.
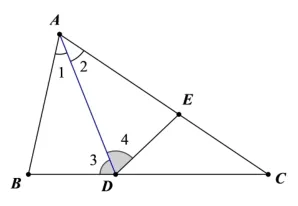
图14
(3)如图15,过AD上一点P做MN⊥AD,分别交AB、AC于M、N,根据“角边角”定理判定ΔAPMΔAPN.或在AB、AC上截取M、N使AM=AN,根据“边角边”定理判定ΔAPMΔAPN(多种方法).

图15
学生很难想到第(3)种方法,教师需要帮助学生打开思维,根据条件创造性地思考解决问题的办法.这个活动能够提升学生的几何直观能力、作图能力、分析问题和解决问题的能力以及逻辑推理的能力.
以上是全等三角形单元教学的设计思路,通过实践发现,学生对全等三角形概念的理解以及全等三角形判定方法的整体认识水平较好,学生思维的逻辑性和完整性不断提升,分析问题和解决问题的能力得到发展.这样的单元教学设计思路不仅在几何学习中适用,在代数学习中依然适用,虽然知识载体不同,但是,学习的基本路径和方法基本相同.在本单元的教学中,开放性的问题和活动贯穿始终,这些有挑战性的任务不断激发学生进行思考,有价值的思维活动一直活跃在课堂中,思维充满创造性,深度学习在持续发生.
