基于低秩分解的网络异常检测综述

李晓灿 谢 鲲 张大方 谢高岗

1(湖南大学信息科学与工程学院 长沙 410082) 2(中国科学院计算机网络信息中心 北京 100190)

互联网已经成为社会基础设施，但面临严重的安全挑战[1]，如拒绝服务攻击[2-3]、蠕虫病毒[4]、僵尸网络[5-6]等.例如，2016年Twitter与Spotify的大型数据中心，因遭受了持续的拒绝服务攻击而关闭网站[8]；2017 WannaCry勒索[7]病毒感染了政府、能源、医院、学校、工厂等多个领域.随着新技术的不断应用，互联网变得越来越复杂，攻击手段越来越先进，如何快速精准地检测定位这些异常行为，避免造成更多的损失与危害，变得尤为重要.

1 研究背景

对于网络异常，不少文献有各自的定义：Thottan等人[9]将网络异常描述为一种偏离正常网络行为的事件；Barnett[10]将异常数据集定义为 “与数据集中其余部分出现不一致的观测子集”；Chandola等人[11]认为异常数据的行为模式不符合既定的正常行为；根据Lakhina等人[12]所述，网络异常表现为在网络流量层面上出现不同寻常且明显的变化，这种变化通常可以跨越多个网络链接；Hoque等人[13]将异常定义为“相较于明确定义的正常行为数据，那些更不符合规定的、更令人关注的行为数据”；Hawkins[14]对异常的定义是“异常是远离其他观测数据而疑为不同机制产生的观测数据”.通过上述定义发现，异常检测本质就是检测和发现数据中不符合期望行为的异常数据模式.研究人员在设计异常检测算法前通常需要判断所需检测异常的种类，通常可分为3类[15-16]：

1) 单点异常(point anomalies).单点异常[11,15]即与全局数据的行为模型不同的单点数据.异常数据在数据集中单个出现，不产生聚集.例如某一局域网中，存在某一网络节点发生拥塞，导致其丢包率远远高于其余网络节点，那么该网络节点即为单点异常.单点异常作为最简单的一种异常种类，通常只需要简单的聚类、分类算法即可进行有效检测.网络中U2R，R2L等攻击[17-18]通常可视为单点异常.

2) 集体异常(collective anomalies).集体异常[19-20]通常由多个对象组合构成，即单独观测某一独立个体可能并不存在异常，但是这些个体同时出现则构成一种异常.集体异常通常是由若干个单点组成，例如，拒绝服务攻击通常由攻击者控制大量傀儡机向服务器发送请求来抢占服务器资源，使服务器无法响应正常请求，达到攻击服务器的目的.

3) 上下文异常(contextual anomalies).上下文异常[21]通常被定义为：当数据点的值与同一上下文环境中的其他数据点明显不同时，该数据点被认为是上下文异常值.值得注意的是，同一个值发生在不同的上下文环境中，可能不会被认为是离群值.当我们讨论日志异常检测任务时，“上下文”通常表示为日志文件所示上下文；而当我们讨论时间序列异常检测任务时，“上下文”则表示时间.因此，在网络异常检测中，日志异常、时序数据异常通常可视为上下文异常.

1.1 相关综述工作

异常检测一直以来都是一个备受关注的问题，不少异常检测的综述论文从不同角度对现有的异常检测方法进行了总结与分析.文献[22]将神经网络异常检测方法划分为特征提取方法、正常数据表征方法、异常分值学习方法，并详细介绍了这些方法解决的异常检测问题中存在的挑战.文献[23]对时序数据检测方法进行了综述，并将这些方法根据变量的不同分类为单变量异常检测与多变量检测.文献[24]则将网络异常检测方法划分为基于距离的方法、基于密度的方法、基于软阈值的方法.而文献[25-26]与文献[27]则分别对基于机器学习以及数据挖掘的异常检测方法进行了综述，并将它们根据具体实现算法的不同进行了归类，如聚类分析、支持向量机、决策树、贝叶斯网络等.

尽管文献[22-27]提出一系列的异常检测综述对现有的大部分异常检测方法进行了归类与整理，但它们大多是基于某一具体的异常检测方法进行分类与总结.近期随着稀疏表征技术的快速发展，得益于该技术较强的数据特征提取能力，基于低秩分解技术的异常检测方法也越来越受到重视，因此，本文将对基于低秩分解的异常检测方法进行综述以及分类.

1.2 异常检测方法原理以及分类

异常检测的基本思想是通过算法将异常和正常区分出来，从距离、密度、概率统计这3个不同的角度来区分正常数据和异常数据.异常检测算法可以分为3类，如表1所示：

Table 1 Classification Table of Traditional Anomaly Detection Methods表1 传统异常检测方法分类表

基于距离的异常检测方法[28-32]是基于数据对象之间的距离计算来定义异常，具有清晰的几何解释.这类方法[31]于1998年被提出，通过计算比较数据与近邻数据集合的距离来检测异常数据，是最常用的异常检测方法之一.其基本思想是正常数据点与其近邻数据相近，而异常数据点则更远[32].这类方法通常不需要数据标签，适用于无监督异常检测场景.其缺点主要包括计算复杂度高、异常距离阈值难以确定等.

基于密度的网络异常检测方法[33-36]，首先需要估算输入空间的密度分布，然后将在低密度空间区域的数据对象定义为异常数据.基于局部离群因子(local outlier factor, LOF)作为一个经典算法[33,36]，通常为每一个数据赋值一个代表其邻域密度的LOF值，当LOF值越大，则表示其邻域密度越低，越有可能是异常数据.这类方法同样不需要数据标签，适用于无监督异常检测场景.其缺点主要包括计算复杂度高、LOF阈值定义困难等.

基于概率统计的异常检测方法[37-41]，最早由Barnett等人[41]提出，首先假设数据集服从某种分布(如正态分布、泊松分布及二项式分布等)或概率模型，然后通过判断各数据点是否符合该分布/模型来实现异常检测.例如，假设数据集服从一元正态分布，当数据点与均值差距大于3倍方差时，则认为该数据点为异常数据.这类方法基于数据分布能够快速有效地找出异常数据，同时又能表示数据所包含的信息特征.其缺点主要包括可解释性差、数据分布/模型难以确定、随着数据特征维度的增加其异常检测精度将降低等.

大量研究基于数据挖掘、机器学习、深度学习等技术实现异常检测过程，由于数据挖掘与机器学习算法存在交叉与重叠，本文将异常检测过程的实现方法分为2类，如表2所示：

Table 2 Implementation Methods and Specific Algorithms of Anomaly Detection Algorithms表2 异常检测算法的实现方法与具体算法

尽管经过多年异常检测方法的研究，很多检测方法都实现了不错的异常检测效果.然而，大部分研究都是通过分析独立的时序数据(例如，单链路流量数据[37]、关键性能指标(key performance indicator, KPI)数据[69-70]、日志/记录[71-73]、数据包[74]、简单网络管理协议(simple network management protocol, SNMP)数据[1,75]等)来实现异常检测.这些研究方法却存在一些不可避免的缺陷[76]：

1) 通常需要学习网络攻击的先验知识(prior knowledge)[77]或分析正常用户的行为模式，因此，难以检测新型异常、模仿正常用户行为模式的攻击.

2) 仅利用了网络数据内部的时间相关性，而忽略了空间相关性，而许多异常行为常影响网络中多条链路或路径，并不会在单链路或路径上明显呈现，这就使得检测并不准确.

3) 通常利用阈值判断检测数据是否为异常，却无法定位异常发生的具体位置，这就使得算法在网络管理的应用中存在局限性.

为了解决上述3个缺陷，Lakhina等人[12,78]提出使用流量矩阵作为数据源，并使用一种主成分分析(principal component analysis, PCA)[79]实现了基于低秩分解的全网(network wide)异常检测模型.该模型利用网络数据所蕴含的低秩性特征，通过从网络监测数据分离低秩正常数据和异常数据，实现全网异常检测.

基于低秩分解的全网异常检测模型不仅利用多条链路流量数据中的时间相关性(temporal corre-lation)，而且同时整合了空间相关性(spatial corre-lation)，将高维的网络流量数据矩阵映射到正常子空间与异常子空间，然后在异常子空间中检测凸显的异常行为模式.该模型作为一种无监督异常检测模型，不需要学习任何网络攻击/异常的先验知识以及网络正常行为模式，同时充分利用了网络数据中的时间-空间相关性.另外，通过分离所得异常数据通常能够实现对网络异常的定位.因此，该模型能够很好地解决传统异常检测方法中存在的一系列局限性问题.

尽管，基于低秩分解的全网异常检测模型相较于传统的异常检测方法具有一定的优势性，却依然存在不少挑战.

1) 基于低秩分解的全网异常检测模型关键在于从监测数据中提取正常数据，然而，异常数据通常严重影响正常数据的低秩性，进而影响正常数据的提取.因此，如何准确提取正常数据，并在进行正常数据提取过程中对异常数据进行有效约束，以减少异常数据对正常数据提取的影响，从而保证异常检测精度，这成为一项挑战.

2) 基于低秩分解的全网异常检测模型通常需要使用低秩分解技术(如矩阵/张量分解)，然而，低秩分解过程通常是迭代执行过程，需要高昂的计算代价.这就降低了该模型的可拓展性，同时使其无法满足在线网络异常检测的要求.因此，如何降低该模型的计算代价成为另一项挑战.

为了更清晰地介绍各类基于低秩分解的全网异常检测模型，本文首先在矩阵模型下对各类异常检测方法，根据其对异常数据约束方法的不同进行分类，并介绍各类模型在计算代价以及求解方式上的变种与改进.然后，以同样的方法对张量模型下的异常检测方法进行了分类与总结.

2 基于低秩分解的异常检测模型原理

2.1 网络监测数据矩阵

为了研究基于低秩分解的全网异常检测技术，通常可以将同一个网络中所有源节点(origin)和目的节点(destination)对之间的性能数据(例如流量、吞吐量、时延等)建模成一个矩阵.如图1所示，矩阵中的行代表源节点-目的节点对(OD对),而矩阵中的列代表时间(time)，矩阵中元素则代表对应时刻下OD对之间监测的网络性能数据.根据所选择的网络节点类型的不同，可以定义为不同粒度的矩阵，例如链路级、路由级、PoP(point of presence)级流量矩阵[80-81].

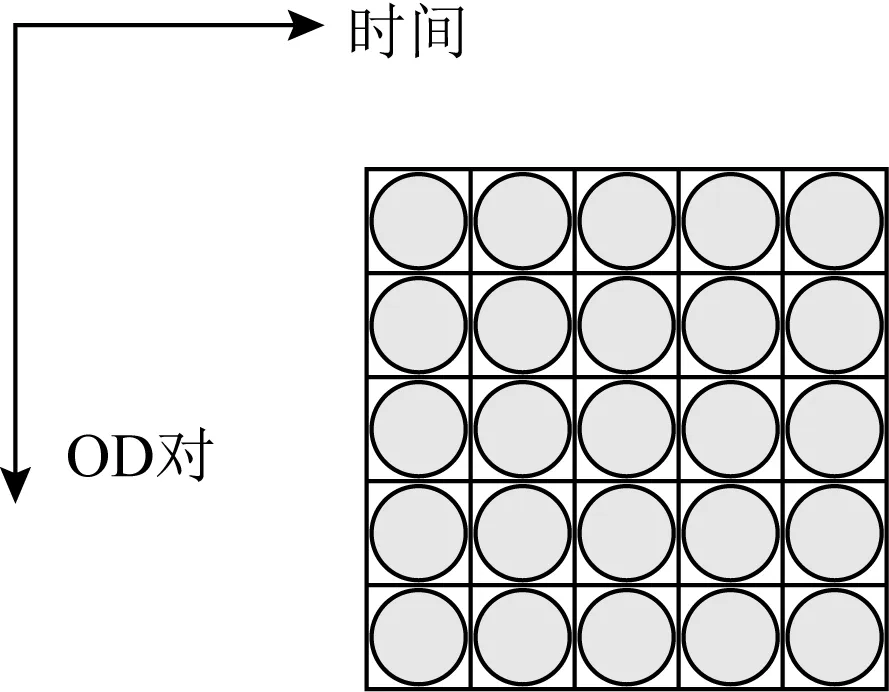
Fig. 1 Network monitoring data matrix图1 网络监测数据矩阵

2.2 网络数据的低秩性分析

基于低秩分解的网络异常检测算法实现的前提条件是将正常网络性能数据建模为低秩数据，因此，本节将首先给出网络测量数据的低秩性验证.

用户的网络行为通常具有时间稳定性以及空间相关性.文献[82]阐述并证明了网络性能数据的时间相关性、空间相关性、天周期性等特征.如图2所示，图2(a)表示相邻时刻之间的网络性能数据之差的累计概率分布，图2(b)表示不同OD对中的网络性能数据的相关系数，图2(c)表示相邻天之间的网络性能数据之差的累计概率分布.

通过分析图2(a)发现，网络性能数据在相邻时刻之间十分相似.图2(c)则显示相邻天之间的网络数据十分相似.因此，网络性能数据通常具有较强的时间稳定性，这就使得网络性能数据在时间维度(例如图1中的时间)具有低秩性的特点.同样地，通过分析图2(b)发现不同OD对之间的网络数据向量具有较强的相关性，因此，网络数据同样具有较强的空间相关性，从而使得网络数据在空间维度(例如图1中的源节点-目的节点对)具有低秩性的特点.

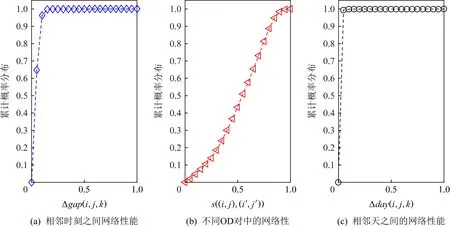
Fig. 2 The temporal correlation, spatial correlation, and day periodic of network data图2 网络数据的时间相关性、空间相关性、天周期性

为了进一步验证网络数据的低秩性，我们将网络性能数据按照图1所示建模为矩阵X，并对X进行奇异值分解(singular value decomposition, SVD)，得到[X]=UΣVT.其中，Σ为对角矩阵，Σ=diag(σ1,σ2,…,σR,0,…,0)，该矩阵的对角线上元素通常为从大到小排列的结果.那么，矩阵X的秩则为矩阵Σ中非零元素的个数.值得注意的是，在实际的应用中，由于网络的监测数据为连续数据存在一定的测量噪音，因此，监测数据通常并不满足严格意义的低秩.根据主成分分析算法的定义，奇异值越大，其所代表的主成分越重要，其前k个奇异值所占比重几乎等于所有奇异值之和时，则可以认为这个矩阵为近似低秩矩阵，并满足低秩性的特点.因此，通常利用指标来判断是否为近似低秩矩阵.

图3表示Abilene和GEANT数据集的低秩性验证结果.通过分析可以发现，少数几个奇异值基本占据了所有奇异值的比重，因此，得以验证网络性能数据具有低秩性特征.

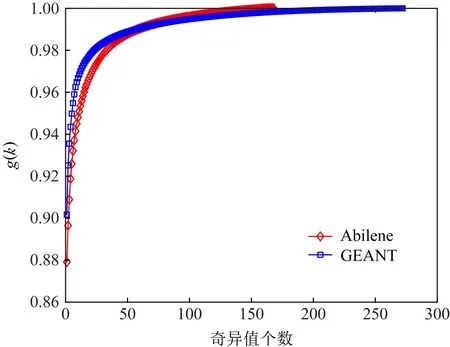
Fig. 3 The diagram of low rank of network data图3 网络数据的低秩性示意图

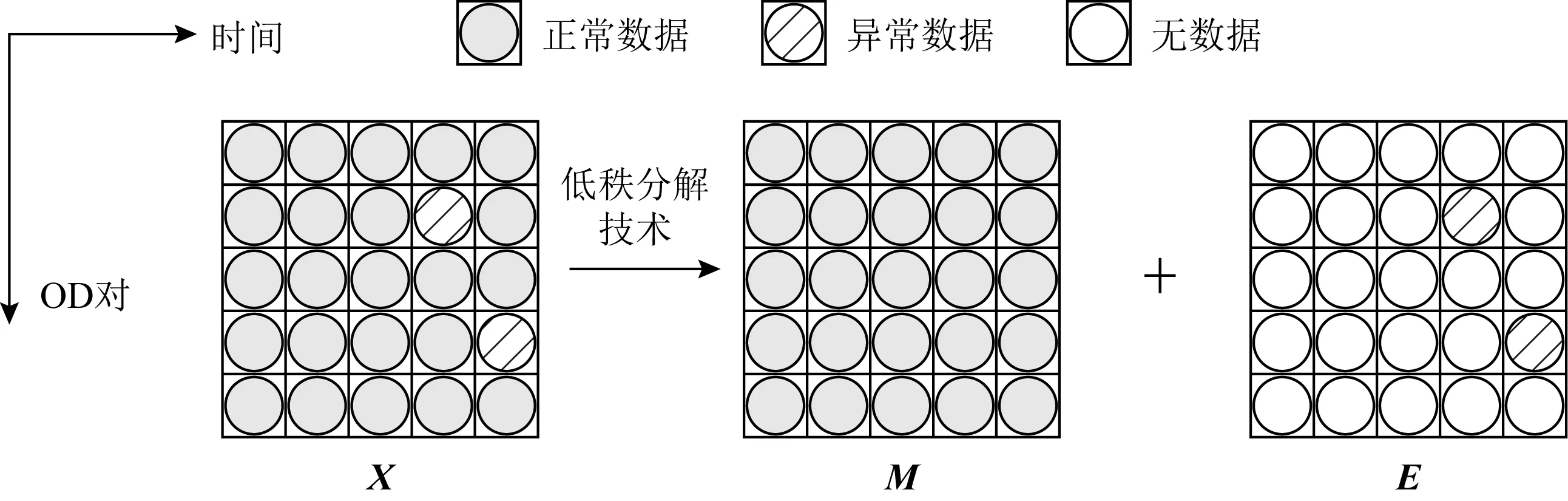
Fig. 4 Network anomaly detection based on low-rank decomposition图4 基于低秩分解的网络异常检测方法

文献[83]同样在开源网络流量数据集Abilene与GEANT上开展了实验，并验证了网络数据的低秩性.另外，大量研究[82-87]利用网络数据的低秩性来填充网络缺失数据.而基于低秩分解的网络异常检测方法则通常利用网络性能数据的低秩性以及低秩分解技术，将高维的网络性能数据映射到正常子空间与异常子空间，其中正常子空间即为低秩子空间.

3 基于矩阵模型的异常检测方法

由于网络性能数据中具有第2节中分析的低秩性特征，因此，基于低秩分解的数据分离模型[88]提出利用网络数据内部的低秩性特征，结合低秩分解技术将监测所得原始数据分离成为正常数据与异常数据.如图4所示，矩阵X为网络监测数据矩阵，利用低秩分解技术可以将其分解为正常数据矩阵M与异常数据矩阵E.根据2.2节分析，正常数据具有低秩性的特点，网络攻击代价高的问题以及网络设备故障的稀疏性问题使得异常数据通常具有稀疏性的特点.因此，异常数据矩阵E通常为稀疏矩阵，通过基于低秩分解的数据分离模型获得稀疏异常数据矩阵E后，即可对网络数据中是否存在异常进行判定，同时根据矩阵中非零元素所处位置可进行异常定位.

为了实现图4所示的数据分离，基于低秩分解的异常检测模型通常将优化目标函数表示为：

(1)

其中,X为原始的网络监测数据，M为正常数据矩阵，E为稀疏异常数据矩阵，rank(M)≤R表示正常数据的低秩约束，而ρ(E)表示异常数据约束条件.由于基于低秩分解的异常检测模型关键在于从监测数据中提取正常数据，然而，异常数据通常严重影响正常数据的低秩性，进而影响正常数据的提取，并最终影响异常检测的精度.因此，如何准确地提取正常数据并有效约束异常数据，成为异常检测的关键一环.

本节将分类介绍各类异常检测方法，如表3所示.根据正常数据的提取方法与异常数据约束条件的不同，将基于低秩分解的异常检测方法分为基于PCA的异常检测方法、基于鲁棒的主成分分析方法(robust principal component analysis, RPCA)的异常检测方法、基于直接矩阵分解的异常检测方法，以及其他异常检测方法.然后介绍各类方法在计算代价以及求解方式上的优化与改进.

Table 3 Classification of Anomaly Detection Methods Based on Low-Rank Decomposition Under Matrix Model表3 矩阵模型下基于低秩分解的异常检测方法分类

3.1 基于PCA的异常检测方法

Lakhina等人[12,78]提出将网络流量数据建模为矩阵，并使用PCA算法来实现全网异常检测.该算法利用低秩分解技术，将正常数据M从原始监测数据X中提取出来，如图4所示.

为了实现正常数据的提取，通常对原始监测数据使用PCA[79]求解式(2)来获得网络监测数据的低秩子空间(UR(UR)T)，并将原始数据投影至低秩子空间，得到正常数据：M=UR(UR)TX.

(2)

为了求解式(2)，研究[12,78]首先计算数据矩阵X的协方差矩阵Cov(X)，然后通过奇异值分解方法得到协方差矩阵的奇异值{σ1,σ2,…,σn}与特征矩阵U，并选择R个最大的奇异值所对应的特征向量(主成分)构成特征矩阵UR，最后将原始数据矩阵X投影到特征矩阵所构成的空间P=UR(UR)T上，从而得到正常数据M.

通过PCA完成正常数据的提取后，为了实现异常检测，基于PCA的异常检测方法又可以细分为基于子空间残差分析的异常检测方法与基于主成分方向变化的异常检测方法两大类，接下来讲具体介绍这2类方法.

3.1.1 基于子空间残差分析的异常检测方法

基于子空间残差分析的异常检测方法[12,78,89-90]，在获得低秩的正常数据M后，为了能够准确检测并定位异常，直接计算原始数据与正常数据之间的残差子空间(X-M)，并对残差子空间进行阈值判断.当残差大于阈值时，则定义该位置为异常数据，否则为正常数据.

下面将介绍2种阈值设计方案[12,78]，首先定义残差子空间中各位置的平方预测误差(squared prediction error,SPE)为

SPE=(xij-mij)2,

(3)

其中,xij与mij分别表示原始监测矩阵与正常数据阵中第i行、第j列的元素值.

基于Q统计量的方法，定义阈值为

(4)

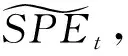
(5)

其中0≤α≤1是历史数据的相对权重，亦称为平滑指数.

(6)

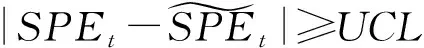
另一方面，由于基于残差分析的异常检测方法需要获得正常子空间的前提是对原始数据进行低秩分解，而这一过程计算代价非常高.文献[91-92]为了让这一类方法更适用于大规模网络的异常检测任务，提出了一种分布式的主成分分析方法，将原本的中心化异常检测转变为分布式异常检测.这种方法为每一个网络监测节点设置一个监测过滤窗口，当且仅当该监测节点中新来临的数据不属于该监测过滤窗口内，才将该数据向中心节点上传于更新.而中心节点则根据各监测节点上传的数据进行参数更新，而不是通过精确的全局数据进行更新，并在更新后将结果下发到各个监测节点.这就使得计算代价大大降低，同时实现了分布式的异常检测.

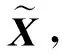
基于子空间残差分析的异常检测方法通常针对全网所有时刻的性能数据进行设计，并通过将原始数据分为正常子空间与异常子空间进行异常检测.在异常子空间内，我们可以判断是否存在异常数据，同时可以通过异常空间定位异常数据所在具体时刻与位置，如图4所示，稀疏矩阵E中第2行第4列的元素，表示第2个OD对在第4个时刻发生了异常.因此这些方法适合部署于网络数据中心的离线异常检测与定位任务中.

3.1.2 基于主成分方向变化的异常检测方法

基于主成分方向变化分析的异常检测方法[95-96]不同于3.1.1节的残差分析方法，这一类方法并不需要计算原始数据与正常数据之间的残差，而仅需对比前后2时刻下PCA所求主成分的变化来检测异常.

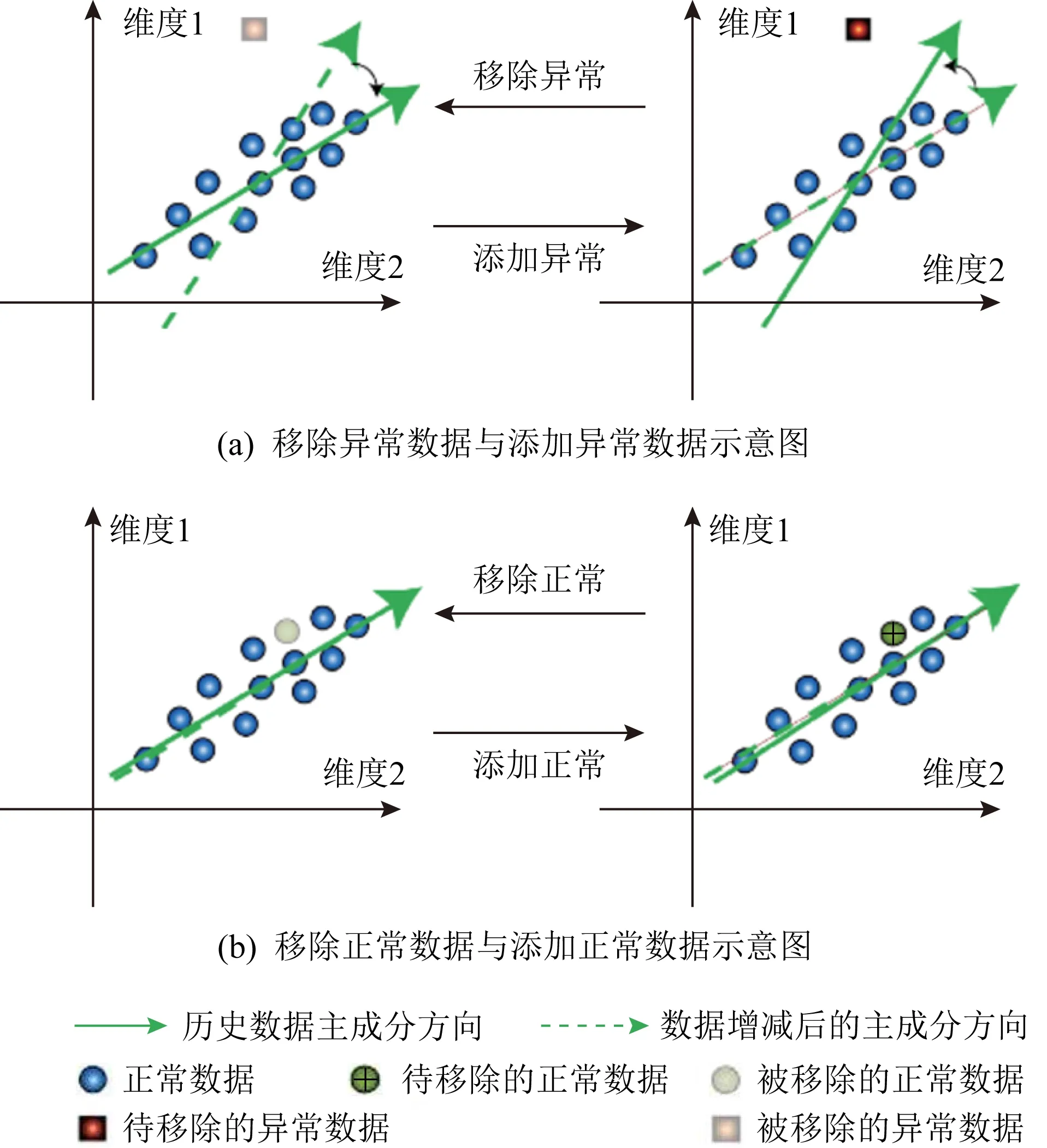
Fig. 5 Diagram of anomaly detection method based on principal component direction change analysis[95]图5 基于主成分方向变化分析的异常检测方法[95]

PCA作为一种降维方法，通常以最小化各个数据样本到主成分之间的距离之和为目的，进行优化求解.以图5为例，降维后的主成分方向表示为图5(a)中左侧图的实线箭头所示的新坐标轴，而原始坐标轴则代表原始空间.图5中的小圆圈则表示历史数据样例，当新的数据样例到来时，将在不同程度上影响主成分的方向，尤其是当新来的数据为异常数据(方块)时，由于新数据严重偏离正常数据，通常会使得主成分的方向将发生巨大的偏移(如图5(a)的右侧图所示)；反之，当新来的数据为正常数据(圆圈)时，主成分的方向则并不会发生较大偏移(如图5(b)右侧图所示).正是利用PCA的这一特性，基于主成分方向变化的异常检测方法通常适用于判别新来临的数据是否为异常数据.

由于传统的PCA通常处理向量类型数据，在实际网络的异常检测任务中，网络数据往往建模成为矩阵模型，传统的PCA需要将矩阵模型向量化，以便检查当前时刻是否存在异常.文献[97]提出，蕴含在数据内部的空间相关性将因为向量化过程出现丢失，因此，文献[97]提出使用双向2维PCA来计算网络数据矩阵的主成分，并利用所求主成分来进行异常检测.

首先，将历史的网络数据通过双向2维PCA，计算得到矩阵行列2个空间的历史主成分uhistory，vhistory.如图6所示，通过双向2维主成分分析方法，原始数据从3维降到2维与1维.时刻t下的主成分由u1(t),u2(t)与v1(t)组成，其中u1(t),u2(t)为行空间主成分，v1(t)为列空间主成分；而时刻t+1的主成分由u1(t+1),u2(t+1)与v1(t+1)组成.

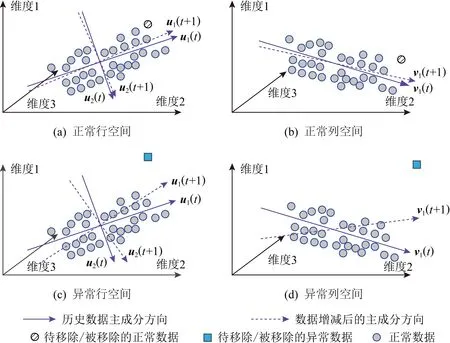
Fig. 6 Diagram of anomaly detection method based on two-dimensional principal component direction change analysis图6 2维主成分方向变化分析的异常检测方法

为了计算主成分方向的偏移，将行列2个空间的主成分进行拼接，然后通过式(7)计算前后2个时刻的主成分方向之间的夹角来定义其偏移量的大小.

(7)

其中,Mt=[Ut,Vt]，Mt+1=[Ut+1,Vt+1]，Vec()为矩阵向量化.最后，通过历史数据的预训练或者专家经验来设定阈值，并与Cosine进行比较，以判断数据是否为异常或是否存在异常.

尽管文献[95-96]所提方法可以准确地检测到一些偏离正常模式较大的异常数据，但随着历史数据的不断积累，新来临的异常数据对主成分方向的影响将越来越小.为了维持新来临数据对主成分方向的影响，文献[95,97]提出一种数据过采样(over-sampling)的方法，将新来临的数据复制α×T遍，并更新主成分unew.其中，α为过采样倍数，一般设置α=0.1，T为历史时刻数.另外，这一方法在计算主成分时需要利用奇异值分解或者特征值分解的方法，通常需要高昂的计算代价.为了实现在线网络异常检测，文献[95,97-100]提出了增量更新的过程，这些更新方法不需要重复地进行主成分计算，不需要保存历史数据，而仅需利用新来临数据直接更新主成分方向.

基于主成分方向变化的异常检测方法通常利用历史时刻的网络性能数据训练主成分，并对新时刻的网络性能数据进行实时分析，通常可以判断数据为异常数据，而无法对异常数据所在位置与时刻进行定位，因此适合部署于网络数据中心或小型网络设备的在线异常检测与告警任务中.

3.2 基于RPCA的异常检测方法

基于PCA的异常检测方法，在异常检测过程并没有对异常数据进行约束，而仅使用Frobenius范数约束所得剩余残差来表征异常数据的分布.Frobenius范数为数据内部各项元素的绝对值平方的总和，即约束数据内部的数值大小，当异常数据符合较小的高斯分布时，异常检测效果可以得到保证.然而，当异常数据中存在较大值(尖锐)时，会在不经意间污染主成分分析的正常子空间(即网络性能数据的低秩性特征)，从而扭曲正常的定义[101]，并最终影响异常检测的精度.

为了解决该问题，并保证异常检测的精度，需要对异常数据进行有效约束.由于网络异常数据具有稀疏性的特点，因此，通常使用L0范数来约束异常数据的分布:

(8)

然而，针对L0范数与rank()的约束求解过程比较困难，为此，基于RPCA的异常检测方法[88,102-106]提出对L0范数与rank()问题进行松弛化处理，使用核范数代替rank()约束来提取正常数据，并使用L0范数的最优凸近似(L1范数)来约束异常数据:

(9)

其中，L1范数表示数据内部的每个元素绝对值之和，这就使得异常检测方法可以在异常数据中存在较大值时，保证网络异常检测的精度.

大量文献提出求解式(9)的方法.例如，基于标准内点法(standard interior point methods)[107]被率先提出来求解该问题，但是由于该方法需要非常高的计算代价，因此并不适合用于大规模矩阵处理；为了让算法更具可扩展性，文献[108]提出了奇异值阈值算法(singular value thresholding, SVT)来处理核范数约束问题；文献[109]所提的迭代阈值方法(iterative thresholding, IT)能够实现可扩展性更高的优化方案，但其收敛速度相对缓慢；文献[110]提出了包括加速近端梯度方法(accelerated proximal gradient, APG)与梯度上升方法(gradient-ascent)，然而这2种算法在实际应用中依然出现了收敛缓慢的问题；文献[111]提出2种增广拉格朗日方法，其中一种为精确增广拉格朗日(exact augmented Lagrange multipliers)能够实现Q-linear的收敛速度，另一种非精确增广拉格朗日(inexact augmented Lagrange multipliers)方法收敛速度与精确增广拉格朗日方法相似，却在低秩分解问题上实现了计算代价的优化，相较于加速近端梯度方法能够提高近5倍的计算速度，然而这2种方法将低秩约束问题与稀疏异常约束问题合并在一起进行优化，而没有将它们作为可分离的2个子问题进行考虑，依然存在缺陷.

为此，文献[112-114]提出了一种交替方向乘子法(alternating direction method of multipliers, ADMM),通过中间变量将2个子问题进行分离求解，从而获得更好的异常检测效果.通过引入中间变量Z将式(10)转化为

(10)

其中中间变量Z为乘子的线性约束，β>0为违反线性约束的惩罚参数，〈·,·〉为标准的内积函数.

最后，各个参数更新为：

(11)

(12)

Zk+1=Zk-β(X-Mk+1-Ek+1),

(13)

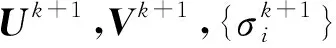
经过对式(9)的研究，不少变种方法被应用于数据分离，并取得了不错的效果.例如，文献[115]提出了一种固定秩的方法，将低秩矩阵的秩固定为r，并提出优化目标函数：

(14)

而文献[116]提出了一种增量秩的方法来改进式(14)的固定秩的方法，这种方法通过逐步增加秩的大小来进行启发式学习，以学习到最优秩，从而实现更高的异常检测精度.

文献[117]提出了一种归纳方法：

(15)

其中矩阵P为低秩投影矩阵，这一优化问题则可通过非精确的增广拉格朗日方法[111]进行求解.

文献[118]提出了使用2维PCA(2D-PCA)来实现异常检测，该方法使用2维PCA替代奇异值分解方法，以实现更多信息的提取从而提高异常检测精度：

(16)

另外，由于网络数据是以流数据的形式源源不断到来的，为了能够实现实时的网络异常检测，文献[119-124]提出了增量更新的方法，这些方法仅需利用新来临的数据更新优化方法中的对应参数，而不需要利用整体数据进行重复计算.这些方法一方面降低了优化算法的计算代价，另一方面降低算法对存储空间的需求，可以使得基于鲁棒的主成分分析方法的异常检测算法更适用于简单网络设备以及在线网络异常检测过程.

基于RPCA的异常检测方法通常针对所有时刻的全网性能数据进行设计，并利用数据分离的方法实现异常检测，因此适合部署于网络数据中心的离线异常检测与定位任务中.其中文献[119-124]所提的改进方案，由于在计算复杂度上进行了有效改进，因此同样适合部署于在线异常检测与定位任务中.

3.3 基于直接矩阵分解的异常检测方法

尽管基于RPCA的异常检测方法被证明对于尖锐的异常数据更具鲁棒性，却利用凸松弛技术来实现对原始约束问题的求解，这就使得异常检测精度仍然较低.原始约束问题为：

(17)

为了直接求解式(17)的原始问题，文献[125]提出了基于直接矩阵分解的异常检测方法，该方法使用块坐标下降(block coordinate descent)方法来求解，将原始问题的求解过程转化为迭代求解2个子问题.

低秩估计子问题：

(18)

异常检测子问题：

(19)

异常检测子问题求解过程为：首先计算原始矩阵X与低秩估计子问题的解M之间的残差S；然后将残差矩阵S中的元素进行降序排序，保留前e个元素，其余位置的元素都置为0，最终得到稀疏异常矩阵E.

文献[126-128]提出一种轻量级的矩阵分解方法，该方法通过实验分析发现基于L0范数的异常检测方法在实际应用过程中呈现一种“异常位置快速收敛”的性质.这种性质使得稀疏异常矩阵E的非零元素所在位置能够快速确定下来，在迭代过程很少发生改变，甚至不改变，而唯一发生变化的是，稀疏异常矩阵中非零元素的大小.正是利用这一性质，所提轻量级的矩阵分解方法可以通过重用上一轮迭代的低秩估计结果，从而降低算法计算代价，以适应更大规模的数据处理.

基于直接矩阵分解的异常检测方法与基于RPCA的异常检测方法类似，利用数据分离的方法实现异常检测，因此适合部署于网络数据中心的离线异常检测与定位任务中.

3.4 其他异常检测方法

除了3.1～3.3节所述的3种不同约束的异常检测方法，少数研究提出了一些特殊范数约束[125-126,128-130]，这些范数约束在不同角度上加强了对异常数据部分的约束，从而提高异常检测算法的精度.

文献[130]提出了card范数来约束异常数据的稀疏性：

(20)

其中，card范数本质上与L0范数一致，该范数通过保留异常矩阵中最大的ε个元素来实现稀疏性约束.

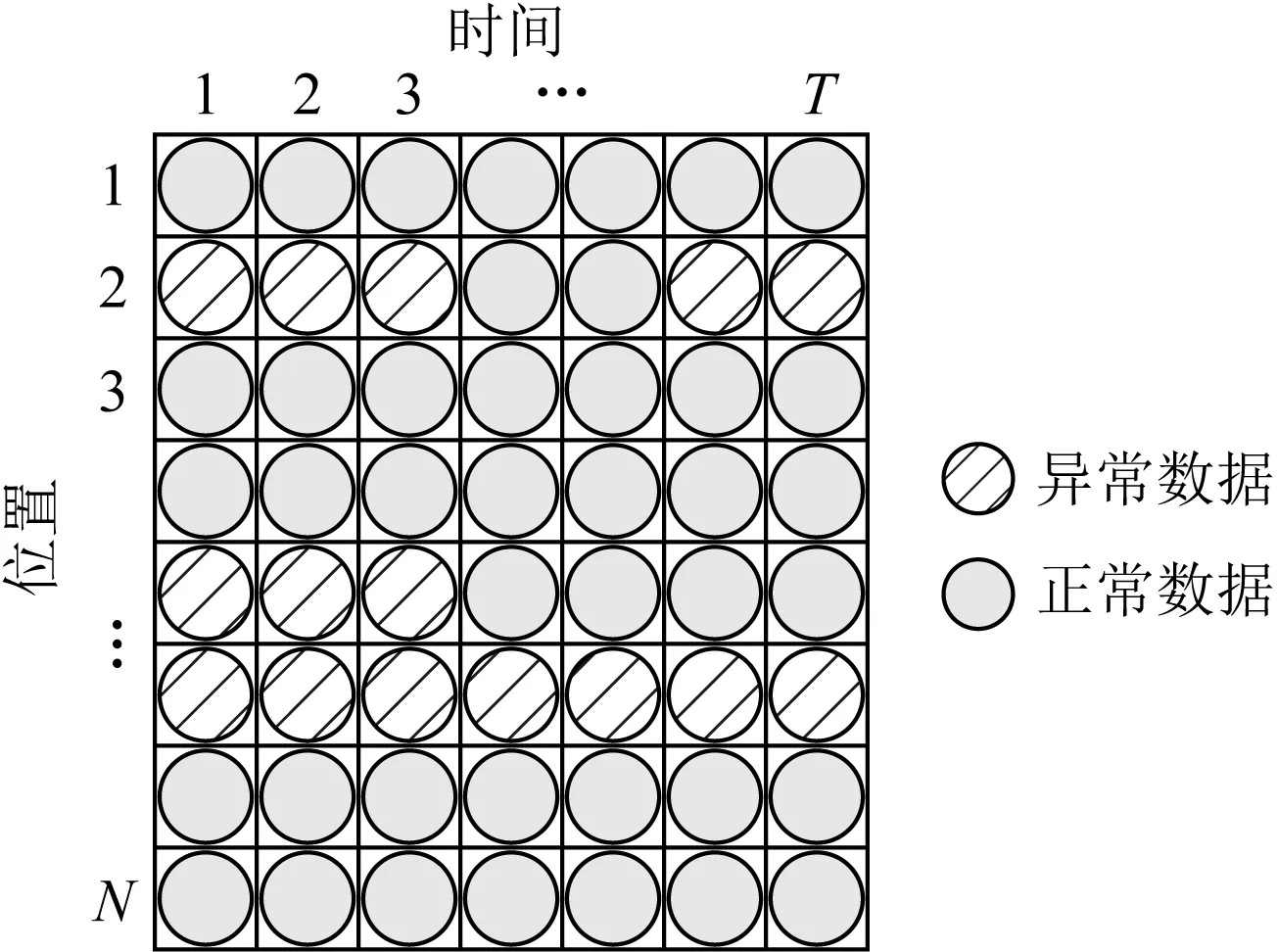
Fig. 7 Structured anomaly model图7 结构化异常模型

在实际网络中，在数据遭到持续污染的情况下会造成矩阵行中多个元素被污染，如图7所示.当第5个位置的数据遭受持续不断的污染时，第5行中所有元素都为异常数据，为了解决这种结构化异常的问题，文献[125-126,128]提出了一种L2,0范数来约束异常数据.

(21)

而为了求解这种约束问题，首先计算原始矩阵X与低秩估计子问题的解M之间的残差S，然后对残差矩阵S的每一行求和，并将每一行的和进行排序，保留最大的ε行，其余行则归0.

如文献[131]所述，文献[88]所提的L1范数与核范数并不是严格的(tight)约束，这就使得所求解并不一定是可信解.为此提出了另外的非凸松弛范数(如式(22)所示)，使用Schatten-p范数来代替核范数约束，使用lq范数来代替L1范数约束，以此加强对正常数据的低秩约束以及异常数据的稀疏约束.

(22)

式(22)同样可以被表达为：

(23)

其中σi(M)表示矩阵M的第i奇异值.该优化问题则通过近端迭代重加权算法(proximal iteratively reweighted algorithm, PIRA)进行求解.

其他异常检测方法利用数据分离的方法实现异常检测，因此同样适合部署于网络数据中心的离线异常检测与定位任务中.另外，由于对异常数据的不同约束，文献[125-126,128]所提出的使用L2,0范数来约束异常数据的方案，可用于结构化的异常检测与定位任务中.

4 基于张量模型的异常检测方法

尽管第3节所述的异常检测方法取得了不错的效果，最近一些研究[82]却表明网络监测数据建模成为矩阵的表征形式，丢失了蕴含在数据内部的高阶结构化信息，难以表征多模式数据的多维本质.而张量模型作为矩阵模型向多维的扩展，可以表征多模式数据的多维本质，张量模型不再局限于数据内比较简单的2维线性关系，而是将多维放到一起综合考虑，探索多因子、多成分、多线性关系，具有重要的学术价值和应用前景.其已经开始被应用到计量化学、信号处理、机器学习、计算机视觉、认知科学等科学领域[132-135].因此，一部分研究为了充分挖掘网络性能数据内部蕴含的高阶结构化特征，提出将网络监测数据建模成为张量模型.

为了能够更简单、清晰地表达，本文将使用3维张量作为例子进行描述，在实际应用中，张量模型的维度可以大于等于3维.如图8(a)所示，3维张量为长方体的模型，其3个维度分别表示源节点、目的节点、时间，其中元素表示对应时刻下OD对之间监测的网络性能数据；在一些研究中3维张量模型则表现为图8(b)的形式，其3个维度分别表示为节点-目的节点对、天、时间，其中元素则表示为某一OD对在某天的某一时刻下监测的网络性能数据.

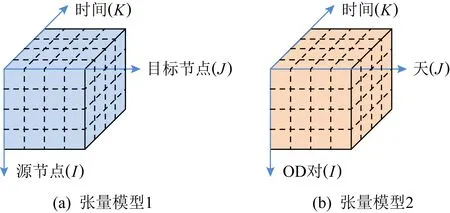
Fig. 8 Network monitoring data tensor图8 网络监测数据张量

正是利用张量模型，大量研究[136-137]通过将基于矩阵模型的算法拓展至张量模型X′，从而实现了更高的异常检测精度.接下来，本节将根据对异常数据的不同约束条件，分类介绍各种异常检测方法并总结分析.

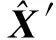
与矩阵模型下的PCA异常检测方法类似，文献[138]的方法更适合部署于网络数据中心的离线异常检测与定位任务中.

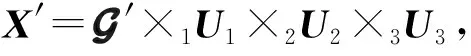
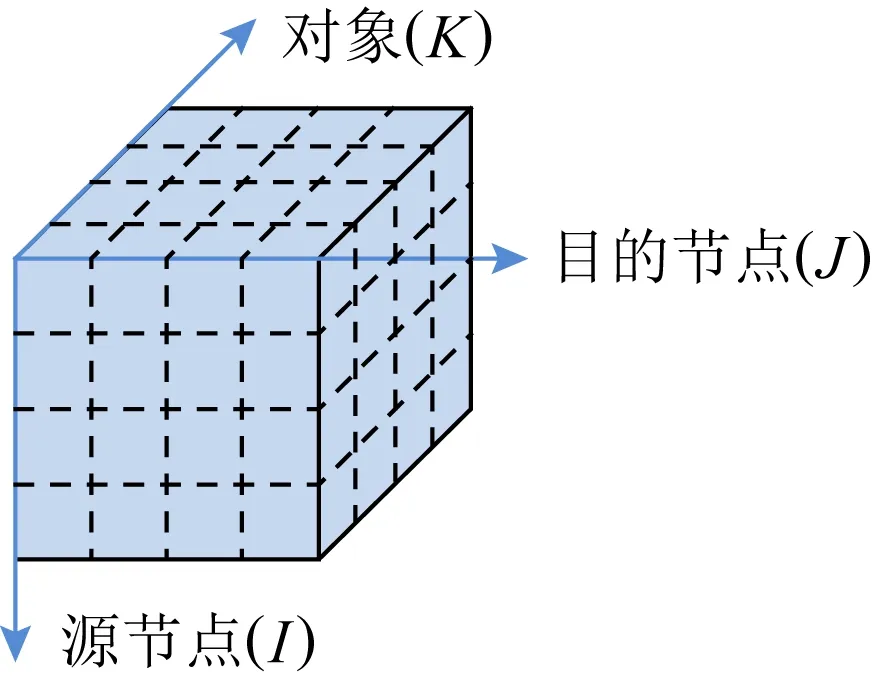
Fig. 9 Origin-destination-subjects tensor model图9 源节点-目的节点-对象张量模型

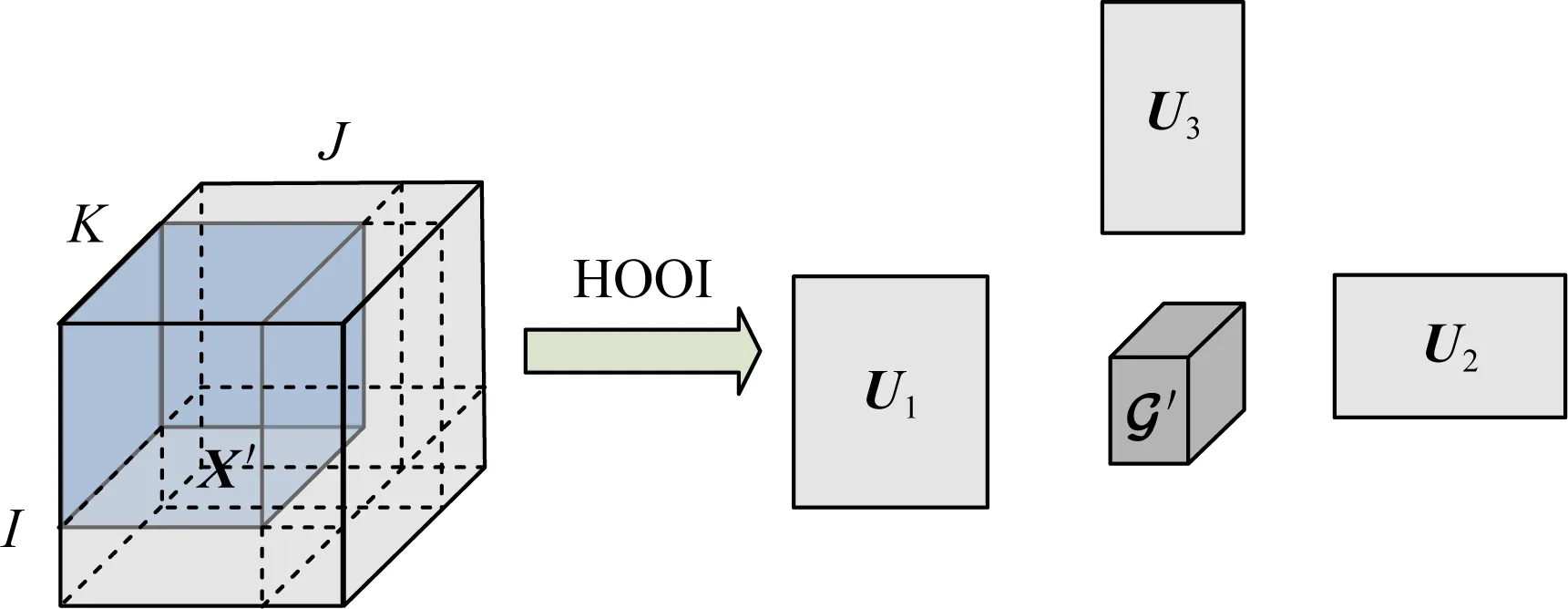
Fig. 10 HOOI tensor decomposition model图10 HOOI张量分解模型

通过分析不同时刻下因子矩阵的变化来判断该时刻是否存在异常，由于不同时刻下的网络接入节点个数不一定相同，使得因子矩阵U1,U2的规模在不同时刻下也不同，也就不能直接使用欧氏距离进行变化的测量，而是使用Grassmann距离[141]来计算：

(24)

其中,ζ为各因子矩阵行数的最小值，而θk(Ui(t),Ui(t+1))则表示因子矩阵Ui(t),Ui(t+1)的Grassmann距离.最后，通过判断该距离是否大于阈值μd+2σd来确定是否为异常，当距离大于该阈值时该时刻下存在异常数据，否则为正常数据.其中

由于文献[140]是基于因子矩阵的差异来实现异常检测，而非数据分离，且HOOI方法的计算复杂度较高.因此该方案更适合部署于网络数据中心的离线异常检测与告警任务中.

相似地，文献[140]将网络监测数据建模成如图11所示的2个张量模型，其中一个为网络流数据构成，另一个为网络拓扑数据构成，张量模型的3个维度分别为源节点、目的节点和时间.

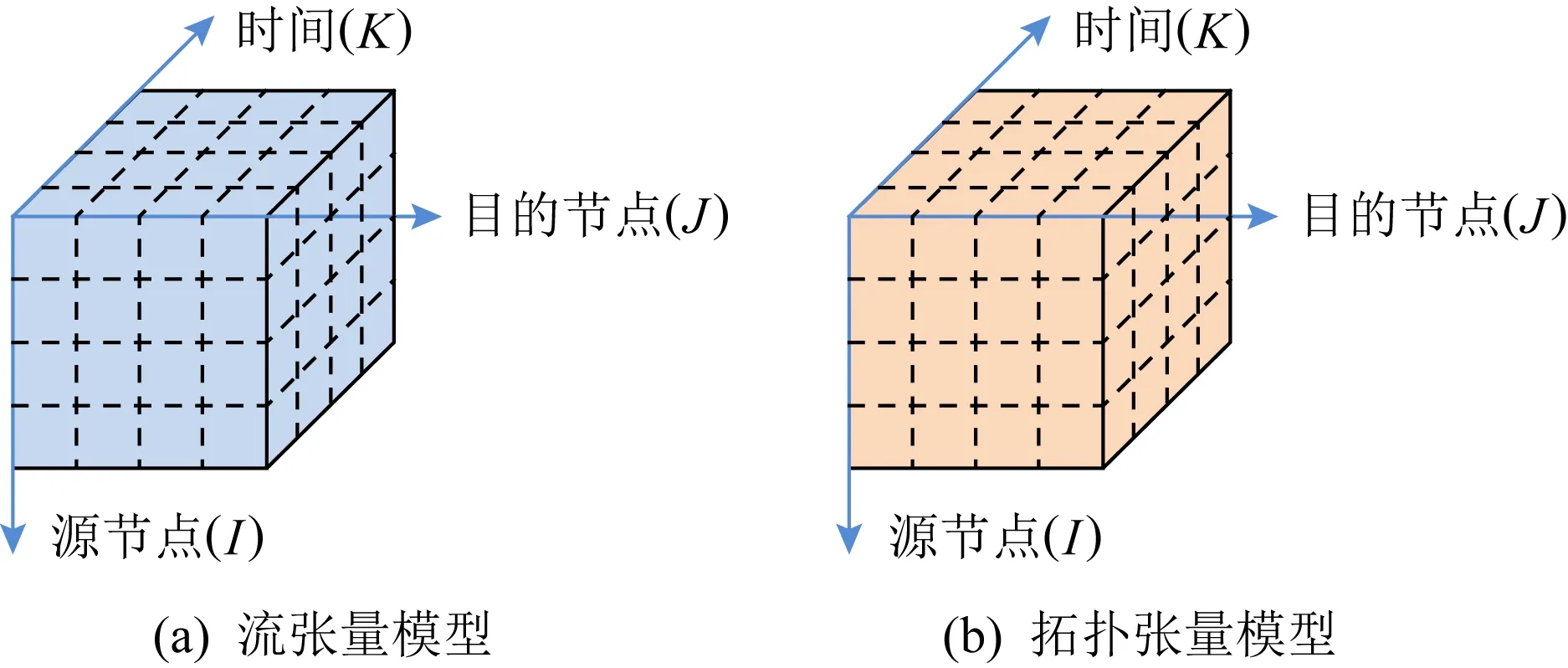
Fig. 11 Network flow tensor model and topological tensor model图11 网络流张量模型与拓扑张量模型

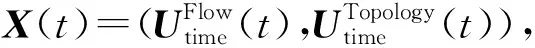
(25)

其中,μ为均值，Cov(X)为协方差矩阵.

同样地，与矩阵模型下基于RPCA的异常检测方法类似，文献[102,142]将数据建模成为高阶张量模型X′,并同样使用核范数与L1范数约束正常数据与异常数据，从而得到优化问题：

(26)

为了求解式(26)的问题，同样采用了增广拉格朗日的方法引入中间变量进行求解.不同的是为了求解张量模型的核范数约束问题，文献[143]首先将张量模型按照各个维度展开，并针对各个维度展开下的矩阵进行奇异值分解，从而得到各自的低秩估计.而文献[102,144]则同样使用ADMM方法进行求解，不同的是,它们结合T-SVD[145]算法进行式(26)的更新.

文献[140,146]同样提出将数据建模成为张量模型，却分别利用CP分解方法和Tucker分解方法来求解张量模型的核范数约束问题，并使用软阈值方法，在更新异常数据张量E时，将张量中小于阈值的元素归为0，以实现稀疏化约束.

与矩阵模型下基于直接矩阵分解方法的异常检测方法类似，文献[147]将网络流量数据建模为张量X′(如图8(b)所示)，并提出基于L0范数约束的张量恢复算法(式(27)所示)，通过学习网络数据中的高阶结构化信息，从而实现更高精度的异常检测.

(27)

其中rank(M′)≤rank(r1,r2,r3)表示该张量在3个不同维度下所形成展开矩阵的秩约束，而E′为L0范数约束的稀疏异常张量.同样地，利用块坐标下降方法将该问题转化为低秩估计子问题与异常检测子问题.不同的是，文献[147]为了快速求解式(27)的多元秩约束的低秩估计子问题以满足大规模网络数据处理的需求，提出了一种连续截断的张量分解方法.

文献[147]所提方法使用数据分离的方法实现异常检测，然而张量分解算法的计算复杂度通常较高.因此，这一类方法更适合部署于网络数据中心的离线异常检测与定位任务中.

尽管文献[147]所提方法能够加速异常检测过程，却仍然无法满足在线的网络异常检测任务.为此，文献[76]提出了一种在线网络异常检测模型，如图12所示.首先将网络流量数据建模成为张量模型，然后定义一个滑动窗口，当新时刻数据来临时，删除窗口内最老的数据，从而保证数据量的同时维持数据的有效性.

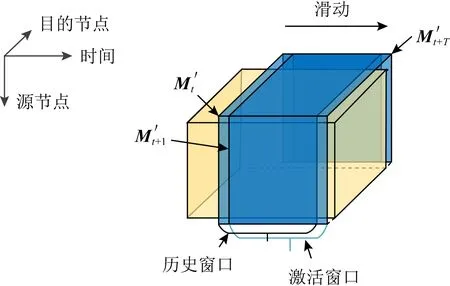
Fig. 12 Online network anomaly detection model图12 在线网络异常检测模型

在新数据来临时，为了能够及时检测并报告异常的位置，文献[76]提出了一种基于CP分解重用的技术，仅需存储少数小规模中间变量，便能够利用新来临数据更新低秩估计子问题中所求解.根据文献[76]所述，该方法能够实现与文献[147]相似的检测精度，却能够满足在线网络异常检测的计算速度要求.

尽管文献[76]所提方案使用数据分离的方法实现异常检测，但是得益于其模型的设计与计算复杂度的大幅度降低，该方法适合部署于网络数据中心的在线异常检测与定位任务中.

根据文献[148]所述，尽管张量模型能够充分网络数据中的高阶结构化信息，却仅考虑了数据内部的线性特征(低秩)，而忽略了可能出现的非线性特征.对于网络数据，源节点域、目的节点域和时间域之间除了线性相关性外，还存在一些非线性邻近信息[84-85,148].例如，同一网络拓扑在某个特定时间(即办公时间、休息时间)应具有相似的流量数据，因此网络性能数据应包含时间邻近信息.而根据节点扮演的角色，网络中的节点可以分为多种不同的类别，例如正常的终端用户和功能强大的服务器.相同类别的节点可能具有相似的网络访问模式，并产生相似的流量负载，从而导致流量数据具有源节点邻近性和目的节点邻近性.因此，文献[148]提出了一种基于流形学习的方法来将这种非线性特征融入异常检测问题中，并提出优化目标函数：

(28)

其中Otime,Oori,Odes分别表示与时间邻近度、源节点邻近度和目的节点邻近度相对应的约束.这3个邻近度分别表示为

(29)

(30)

(31)

其中A,B,C为CP分解中因子矩阵，而La,Lb,Lc分别是时间邻居图、源节点邻居图、目的节点邻居图的拉普拉斯矩阵.

5 方法比较

网络空间安全已经成为国家安全的重要组成部分，异常检测成为网络管理的重要部分之一.而数据挖掘、机器学习、深度学习等领域的快速发展为网络异常检测提供了坚实的理论依据.基于低秩分解的网络异常检测作为一种无监督的异常检测方法，吸引了越来越多的学者们进行深入研究.然而，不同的方法由于约束条件的不同和优化求解方式的不同，达到异常检测精度与计算速度也不同.本节将对基于低秩分解的网络异常检测方法进行了总结以及优缺点的分析，如表4所示：

Table 4 Classification, Summary, Advantages and Disadvantages of Anomaly Detection Methods Based on Low-Rank Decomposition表4 基于低秩分解的异常检测方法分类、总结、优缺点分析

6 挑战与展望

近年来，尽管基于低秩分解的网络异常检测受到了越来越多学者的关注，各种新的研究方法与成果不断涌现，但当前的异常检测研究还处于学术研究的阶段，基于低秩分解的网络异常检测仍然面临着诸多挑战.例如，异常检测方法对于网络特性与领域知识的融合问题，异常检测算法与模型的适应性问题，以及异常检测的后续任务研究问题.这些挑战将推动这一研究方向往更深入的方向不断发展.总的来说，未来的研究方向将主要包括3个方面：

1) 网络特性与领域知识的融合问题.现有基于低秩分解的异常检测模型通常仅约束了正常网络数据的低秩性与异常数据的稀疏性等特点，缺乏对实际网络环境中存在的特征约束，例如网络连通性约束、网络带宽约束、网络流量约束.而这些网络特有的约束通常能够帮助网络管理中心判断数据的正常与否，以及协助网络数据轮廓、特征、模型的构造.另外，网络异常检测模型可以分析与利用的计算机网络领域知识越来越丰富，例如网络拓扑信息、网络设备信息等.

然而，网络特性与领域知识通常并不能表示为欧氏空间数据，难以融入现有的方法.因此，如何设计算法模型，将计算机网络特性与领域知识融入基于低秩分解的异常检测模型中，并提出对应的求解方法，以提高异常检测精度是未来的研究方向之一.

2) 异常检测算法与模型的适应性问题.现有的算法与模型在数据与设备上存在一系列适应性问题.例如，基于低秩分解的异常检测方法通常建立在数据的完整性上，当数据存在大量缺失时，其异常检测的精度会遭到较大的影响.一方面，完整的网络数据采集代价较大，另一方面，数据在传输过程中往往会存在不可避免的丢失，所以网络数据通常会存在缺失的问题.而对存在缺失的网络数据环境进行异常检测充满了挑战.因此，如何设计算法在数据缺失的情况下准确分离正常数据与异常数据，从而保证异常检测精度，将会是未来的研究方向之一.

另外，在实际网络中，网络设备的存储代价与计算代价有限，现有的基于低秩分解的异常检测算法大多针对网络监控中心设计，需要较高的计算以及存储能力.因此，如何将现有算法模型进行压缩，而不损失其异常检测精度，以保证简单网络设备能够进行分布式的异常检测，减少对网络监控中心的依赖，将会是未来的研究方向之一.

3) 基于异常检测的预测分析与根因分析问题.现有的网络异常检测方法通过分析测量到的网络数据来实现，却无法对网络异常进行有效预测.在网络管理中，如何对网络异常进行预测，并根据预测结果进行事先诊断与预防十分重要.因此，如何通过对历史异常数据的分析，来预测未来发生异常的位置以及时间，是未来的研究方向之一.

另外，在实际的网络管理场景中，通过基于低秩分解的网络异常检测方法可以分离得到稀疏异常数据.尽管可以通过稀疏异常数据进行异常定位与检测，却无法进行进一步的异常根因溯源以及有效进行恢复与管理.因此，如何通过分析发生异常的种类、分布以及时间来确定发生异常的根因，是未来的研究方向之一.

作者贡献声明：李晓灿负责论文的撰写与修改；谢鲲负责论文结构设计与指导，以及论文部分章节的修改；张大方负责各方法的整理与校对，以及论文修订；谢高岗负责部分章节内容的撰写与修改.