基于张量分解的噪声抑制算法研究

宋毅梁

（四川大学计算机学院，成都610065）

0 引言

高光谱图像是一种被广泛运用在植被勘探、地质检测、农业、军事、天气等领域的成像手段。不同材质的物体其分子和原子的排列决定了其本质的特征，而当电磁波摄入到不同的物质上，其物质的分子、原子排列特征、震动等会让物体呈现不同的光谱吸收与反射的特征。而高光谱成像便是运用这一特点，运用大量的窄波波段的电磁波（<10nm），得到一个带有大量不同波段数据信息的三维数据块。在空间图像维的图像与一般的图像没有分别，而对于光谱维来说，图像的每一个像元都有大量的不同波段的光谱信息。

在日常采集高光谱图像信息的过程中，因为采集时采集通道可能因为这个过程中产生的热噪声使得原本的图像被噪声污染，而高光谱图像数据在有噪声污染的情况下会给后续的数据分析带来很大的障碍。因此去除这类加性噪声会为之后的数据分析带来便利。

传统的噪声抑制方法，把张量数据的二维图像以光谱维展开成二维的矩阵，之后运用矩阵的低秩先验的特点，对图像进行PCA等降维去噪。而这种去噪方式并没有考虑到图像的光谱维之间的联系，会损失掉不少的图像结构信息。因此基于张量代数的去噪方式是当前高光谱图像噪声抑制的重点课题。

目前主要的基于张量代数的算法有Tucker分解和CP分解两种方式。基于Tucker3的噪声抑制方法包括低秩张量近似LRTA[1]、遗传核张量分解[2]，以及多维维纳滤波[3]。基于CP分解的噪声抑制方法有并行因子分析（PARAFAC）[4]和秩-1张量分解[5]。除此之外基于高阶张量图像数据的小波分解噪声抑制方法因其良好的细节保留特性也被大量提出[6-8]。这些噪声处理方式对于受到高斯白噪声影响的HSI图像的信号空间还原是比较高效的。但是在遇到完全丢失像素信息的椒盐噪声、死像素等则不能有效处理。而近年以来提出的鲁棒性主成分分析（RPCA）[9]，这种方法已经被验证可以在传统图像上对稀疏噪声进行有效的噪声抑制还原原始信号。而这种方法的高阶推广也被人提出并且用在稀疏噪声的HSI图像的噪声抑制上。TRPCA[10]用 || ||Z*张量的核范数TNN被用于描述张量的秩。除此之外还有基于TV全变差等方法的提出。本文针对目前已经出现的基于张量分解的噪声抑制方法进行了分析和效果对比。

1 张量基本概念与分解模型

1.1 张量的基本概念

（1）张量的mode-n展开

张量的mode-n展开是把张量的第n个mode的纤维（fibers）作为展开矩阵的列向量然后把这些mode的纤维顺序排列。一个张量X∈R I1xI2xI3的mode维展开为x(n)∈R I n xM n，其中Mn=I1X….I n-1XI n+1….I N。

（2）张量的mode-n乘积

张量X∈R I1X…XI N与矩阵U∈R JXI n的mode-n的乘积被表示为XxnU，实质上是张量的n-mode的纤维（fi⁃bers）与矩阵相乘。因此有公式：

（3）秩-1张量

秩-1张量表示N个矢量进行外积得到的张量，而外积之后的张量阶数取决于外积矢量的个数，其形式为：

此为N阶的秩-1张量。

1.2 张量分解模型

（1）Tucker分解

Tucker分解是奇异值分解（SVD）的高阶推广，一个三阶张量的Tucker分解会把张量X∈R I1×I2×I3会被分解为一个核张量G∈R M×N×J和三个分别对应三个mode做乘积的系数矩阵A∈R I1×M、B∈R I2×N与C∈R I3×J。其分解的表示形式为：

此外对张量的mode积而言，对对应的mode做乘积相当于在这个mode上做投影。

（2）CP分解

CANDECOMP/PARAFAC分解（简称CP分解）这种分解会把张量分解为秩-1张量的和。而张量的CP-秩被表示为分解的秩-1张量的个数。

2 张量噪声抑制算法

2.1 基于Tucker分解的LRTA算法

LRTA算法运用主成分分析（PCA）的思想扩展到高阶的HIS三阶张量图像数据上，通过估计信号空间的维度在降维后还原原始图像。令加性噪声在对每个mode的投影中与信号空间分离以此在达到收敛条件之后得到估计信号的结果。

一般的高斯噪声模型认为采集图像所携带的噪声是一种加性噪声，而想要去除高斯白噪声这样的加性噪声，重要的就是把采集到的数据投影在算法估计的信号空间上。在PCA里，这样的投影工具是一个矩阵它把二维图像数据降维投影得到最逼近原始信号的数据。而对于三阶张量数据来说，对各个mode进行投影则是在各个mode上进行mode-n乘积。因此问题的关键在于得到每个mode对应的投影矩阵p（i）。估计的信号空间数据被表示为：

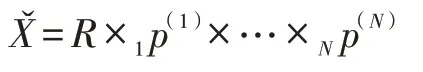
而每个mode对应的信号空间的投影需要先知道每个mode信号空间的维数K n，这些维数的确定依赖于张量Tucker-秩。(K1,…,K N)每个mode的秩被作为衡量Tucker分解的张量秩。而基于高阶PCA思想的这种去噪方式所要处理的其实是如下的优化问题：

显然求张量的秩是一个非凸的问题，因此要变为可求解的优化形式：

张量的核范数是张量沿每个mode展开之后求得的奇异值之和。而最小化核张量SNN则是满足低秩先验的条件。

LRTA算法描述：

（1）input：高光谱HSI张量数据R，以及被估计的投影空间(K1,…,K N)

2.2 基于CP分解的噪声抑制算法

基于CP分解把张量分解为秩-1张量的想法，提出把张量分解为带权值的秩-1张量。认为张量的信号空间是一组高度相关的秩-1张量组成的，噪声则在光谱域的相关性较小。

通过CP分解后得到的带权值的秩-1张量：

其中M是采集信号R的CP分解所需要的秩-1张量的总个数，而αr则是每个秩-1张量所占信号空间表达的权值。要通过R求解未被噪声污染的信号关键在于求解张量的秩。而与矩阵不同，张量的秩在目前还没有明确的定义形式[11]。

不同于Tucker的各个mode上的秩表示张量的秩，而是分解后秩-1张量的个数被表示为了张量的秩序。又因为该方法认为噪声以加性信号为前提而高斯白噪声在信号空间里是并不相关的因此存在的权值很小，而信号空间因为在光谱空间上高度相关因此权值占得比重更大，得到的被估计的信号空间可以表示为：

K表示的是代表信号空间的秩-1张量的个数，也是权值最大的K个秩-1张量。

而W、V同理可以根据上边的方式迭代跟新，最终当这一次迭代减去上一次迭代的值满足条件时就可以跳出得到估计的信号张量数据X̌。

R1TD算法描述：

（1）input：高光谱HSI张量数据R，以及被估计的秩-1张量个数K，最大迭代数M

（2）循环t=1→M

2.3 Tucker-秩与CP-秩的估计方法

（1）AIC赤池信息准则

AIC是一种优秀的模拟统计信息的一种标准[12]，因为张量秩的定义不像矩阵一样明确，因此AIC用于估计拟合各个mode上的统计信息，即Tucker-秩。

（2）CP分解秩-1张量的估计

秩-1张量定义的秩不能通过计算每个mode的统计信号拟合来直接得出。需要利用信噪比得到：

Ki是由AIC得到的每个mode对应的统计拟合SNR是张量的信噪比，而在输入条件并不知道信号空间的时候，信噪比可以通过求统计算法的结果得到近似的评估。

（1）在张量中准备一个移动窗口，5×5、7×7等，计算部分图像区域的方差，得到最小的方差，把这个方差作为噪声的统计信息估计。

（2）求出信号统计信息的估计：

3 Tucker与CP的抑制效果对比

本节运用的HIS图像数据为Washington DC Mal,Indian Pine高光谱图像数据集合，对图像添加加性的高斯白噪声在不同波段的图像分别应用LRTA和R1TD两种基于张量分解的噪声抑制方法进行去噪声，通过对图片细节与峰值信噪比PSNR等图像效果指标进行评估对比。

图1

图片从左到右依次为（1）原始图像211光谱波段（2）加入高斯白噪声之后的211光谱段图像（3）LRTA处理之后的211波段图像PSNR为29.603（4）R1TD处理之后的211波段图像PSNR为33.011

图像在进行了张量的低秩分解处理之后噪声得到抑制，不过两种方法都基于低秩的去噪方法因此在细节上并没有得到很好的保留。

4 结语

本文对主流的两种张量分解的噪声抑制方法进行了阐述并分析了其工作原理，并且利用Washington DC Mal，Indian Pine高光谱数据集进行了仿真。利用PSNR等方法对噪声抑制之后的光谱波段进行了对比。通过实验与对比之后发现在进行这两种方法之后，去噪过程实际上是在降低数据的维度，不可避免地会造成细节的丢失因此未来的工作可以如何对细节尽可能地保留等课题上。