一致性引导的自适应加权多视图聚类
2022-07-12林毓秀张彩明
于 晓 刘 慧 林毓秀 张彩明
1(山东财经大学计算机科学与技术学院 济南 250014) 2(山东省数字媒体技术重点实验室(山东财经大学) 济南 250014) 3(山东大学软件学院 济南 250014)
聚类是数据挖掘中的一项重要任务,将相似的点划分到同一簇中,相异点划分到不同簇中.聚类在信息检索[1]、医疗诊断[2]、社交网络分析[3]、图像分割[4]等领域都发挥着重要作用.传统的单视图聚类算法已遇到瓶颈,在过去的几年中,多视图聚类成为前沿研究.
多视图聚类利用多视图数据中的信息来进行聚类.多视图数据从多个角度来描述同一事物,随着技术的进步,近年来这类数据日益增多.例如,可以同时使用多个设备对同一事物进行拍摄,得到的多个图像属于多视图数据.再者,同一张图像可以使用不同的特征来表示,多种特征形成的数据即为多视图数据.通过使用多视图数据,多视图聚类能够利用不同视图之间的互补信息,从而可能提高聚类的效果.
迄今为止,研究人员已提出大量的多视图聚类算法,大致包括基于多核学习的算法[5-7]、基于矩阵分解的算法[8]、基于图学习的算法[9-10]、基于谱聚类的算法等.其中,基于谱聚类的多视图聚类算法也可称为多视图谱聚类算法,该类算法将谱聚类的思想应用到了多视图数据的聚类中,通常可以分为4类:第1类是为所有视图的数据生成一个一致的相似度矩阵,然后利用谱聚类算法得到聚类结果.有些算法[11-13]直接从原始数据中为所有视图学习统一的相似度矩阵,还有一些算法利用核函数[14]或k近邻图[15-16]等方式先为每个视图构造相应的初始相似度矩阵,然后从中学习一致性相似度矩阵.第2类是为各个视图的数据生成相应的相似度矩阵,再利用各视图的相似度矩阵生成一致的拉普拉斯矩阵[17],从拉普拉斯矩阵中生成划分矩阵,使用k均值聚类算法得到聚类结果.第3类是为每个视图构造好相似度矩阵后,直接利用谱聚类的思想,为所有视图学习统一的划分矩阵[18],然后使用k均值算法进行聚类.第4类是基于协同训练的思想[19],利用视图间的互补信息进行聚类.尽管该领域已有大量研究成果,但仍然存在不少挑战.首先,原始数据通常包含冗余信息和噪声,很多算法忽略了这一问题.其次,在聚类过程中,每个视图扮演的角色是不同的,不少算法将各个视图同等对待.为了解决这些问题,本文提出了一种基于Markov链的多视图谱聚类算法——一致性引导的自适应加权多视图聚类(consensus guided auto-weighted multi-view clustering, CAMC),主要思想如图1所示.由图1可知,该算法首先为原始数据的各个视图构建转移概率矩阵,然后为所有视图学习一致性转移概率矩阵,最后执行谱聚类算法.目标是为各视图学习不同权重,并得到所有视图的一致性邻接矩阵.
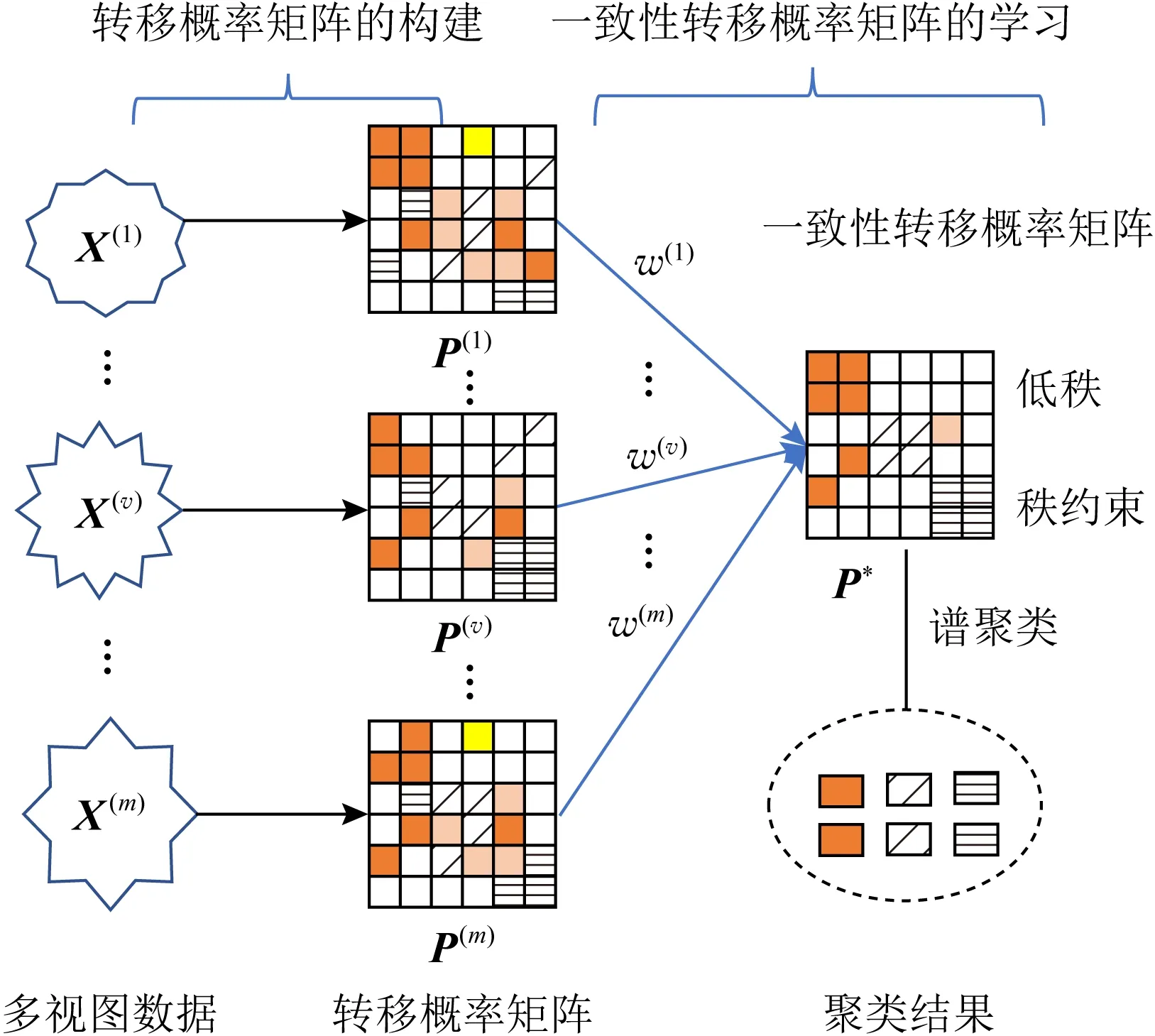
Fig. 1 The framework of CAMC图1 CAMC的整体框架
本文的主要贡献有3个方面:
1) 为每个视图构造一个转移概率矩阵,以减小原始数据中的冗余信息和噪声对聚类性能的影响.
2) 以自适应加权的方式获得一致性转移概率矩阵,并对一致性转移概率矩阵的拉普拉斯矩阵进行秩约束,以确保拉普拉斯图中连通分量的数目与聚类的数目完全相等.
3) 在人造数据集上证明了CAMC是有效的;在7个真实数据集上的大量实验表明,CAMC算法在聚类性能方面优于其他单视图和多视图聚类基准算法.
1 相关工作
为了更加方便地介绍后面的内容,本文在表1中对文中的符号进行了说明.由于本文提出的算法属于基于Markov链的谱聚类算法,故在本节对该类算法的相关工作进行介绍.

Table 1 The Meaning of Notations表1 符号及含义
目前,已有研究[20-21]在聚类和Markov链之间建立了联系.给定n个数据点的单视图数据矩阵X∈d×n,X的相似度矩阵用S表示.计算S的一种常见方式是其中,i,j∈(1,n),xi,xj分别表示第i、第j个向量,σ是标准差.之后构建图G=(V,EG,S),其中V是顶点集,EG是边集,S用来表示边的权值.转移概率矩阵定义为P=D-1S,其中D为对角矩阵,从Markov链的角度来看,pij是从节点Nodei一步到达节点Nodej的随机行走概率,图G存在平稳分布π,其中谱聚类就是对图G进行划分,使Markov随机行走尽量在同一簇内进行.关于基于Markov链聚类的详细信息,请参考文献[20-21].
在基于Markov链的多视图聚类研究方面,Xia等人[22]提出了鲁棒多视图谱聚类法(robust multi-view spectral clustering, RMSC).RMSC通过低秩和稀疏分解从所有视图的数据中恢复了潜在的转移概率矩阵,并将其作为相似度矩阵,使用谱聚类得到最终的结果.RMSC的目标函数为:

(1)
其中,P(v)表示第v个视图构造的转移概率矩阵,P*是学到的转移概率矩阵,E(v)是第v个视图中学到的转移概率矩阵和构造矩阵之间的误差.
Wu等人[23]提出了多视图谱聚类的本质张量学习法(essential tensor learning for multi-view spectral clustering, ETLMSC).ETLMSC将各个视图得到的转移概率矩阵叠成张量,对张量施加核范数的约束,确保张量的低秩性质,并对张量进行旋转来探索不同视图之间的关系.ETLMSC的目标函数为:

(2)

尽管这些方法取得了不错的结果,但仍有很多方面需要改进.从式(1)中可以得知,RMSC将各视图平等对待,忽视了视图所起作用的多样性.ETLMSC使用张量来探索各视图之间的关系,但是当计算最终的相似度矩阵时,直接将张量切片进行平均,忽略了各视图之间的差异.由于我们提出的算法CAMC更为接近RMSC,故在实验部分使用RMSC与CAMC进行对比.
2 一致性引导的自适应加权多视图聚类
2.1 算法思想
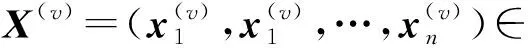
基于Markov链的谱聚类算法很关键的一个环节是获得最终转移概率矩阵.本文使用文献[24]中的算法为每个视图学习相应的转移概率矩阵,在RMSC的启发下,利用核范数确保学到的一致性转移概率矩阵P*是低秩的.该方案的表达式为:
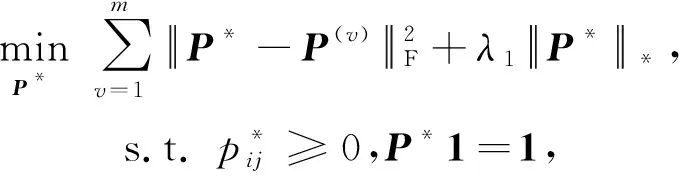
(3)
其中,i,j∈(1,n).但是,这种方式忽略了各视图之间的差异性,故为每个视图分配了权重,即
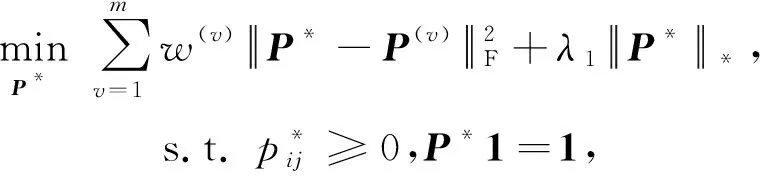
(4)
其中,w(v)是第v个视图的权值.
受到自动分配权值策略[9,25]的启发,本文提出了一种自适应加权的策略来学习一致性的转移概率矩阵.令w(v)为

(5)
则式(4)等价于
(6)
式(6)所学到的转移概率矩阵中相连部分的数量是不确定的.假设簇的数量是c,为了使P*恰好有c个相连部分,对P*的拉普拉斯矩阵的秩进行约束.目标函数表达式设计为:
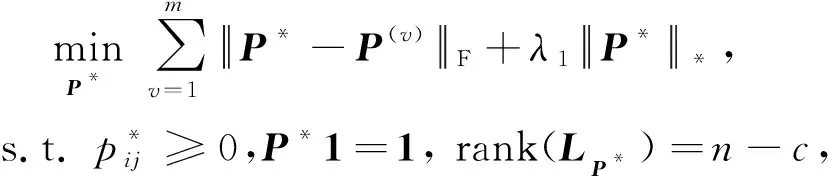
(7)
其中,LP*表示P*的拉普拉斯矩阵.

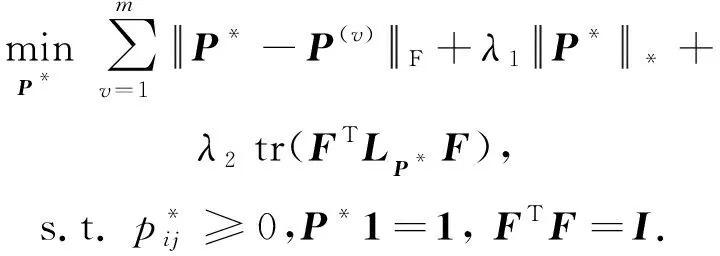
(8)
如图1所示,CAMC先为原始数据的各个视图构建转移概率矩阵;然后,利用式(8)为全部视图学习一致性转移概率矩阵;最后,将其作为输入执行谱聚类算法,得到聚类结果.所学的一致性转移概率矩阵如图2所示,同一簇内的点之间存在转移概率,不同簇之间转移概率值为0,一致性转移概率矩阵的秩等于簇的数目.
Fig. 2 An example of the consensus transition probability matrix P*图2 对一致性转移概率矩阵P*的示例
2.2 优 化
CAMC的目标函数为式(8),其等价于
(9)
其中,w(v)的值见式(5).
为了求解式(9),本文采用交替方向乘子法(alternating direction method of multiplier, ADMM)[27]设计优化策略.将矩阵变量Q作为辅助变量来替代核范数中的P*.式(9)可转化为:
(10)
式(10)的求解可以转换为求解5个子问题.
1) 求解w(v),将其他变量固定,w(v)的值见式(5).
2) 求解P*,固定其他变量,关于P*的目标函数变为
(11)
其中,Y是拉格朗日乘子,μ是惩罚项参数.对于不同的i,该问题是独立的,故而有
(12)


(13)
式(13)可以通过投影算法[28]求解.
3) 求解F,固定w(v),Q,P*时,F的值可以通过求解问题得出:

(14)
找出LP*的c个最小特征值,对应特征向量为F的解.
4) 求解Q,当w(v),P*,F固定不变时,式(9)变为

(15)
式(15)等价于
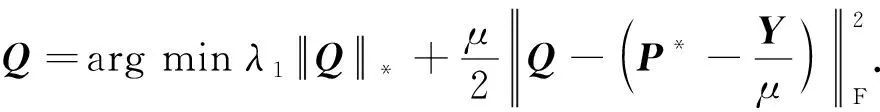
(16)
式(16)可通过奇异值阈值法[29]进行求解.
5) 更新乘子Y和惩罚项参数μ:

(17)
上述5个子问题是求解目标函数式(9)的核心内容.CAMC的算法流程如算法1所示:
算法1.CAMC.
输入:多视图数据集X,超参λ1和λ2;
输出:聚类结果.

② 为每个视图构建转移概率矩阵;
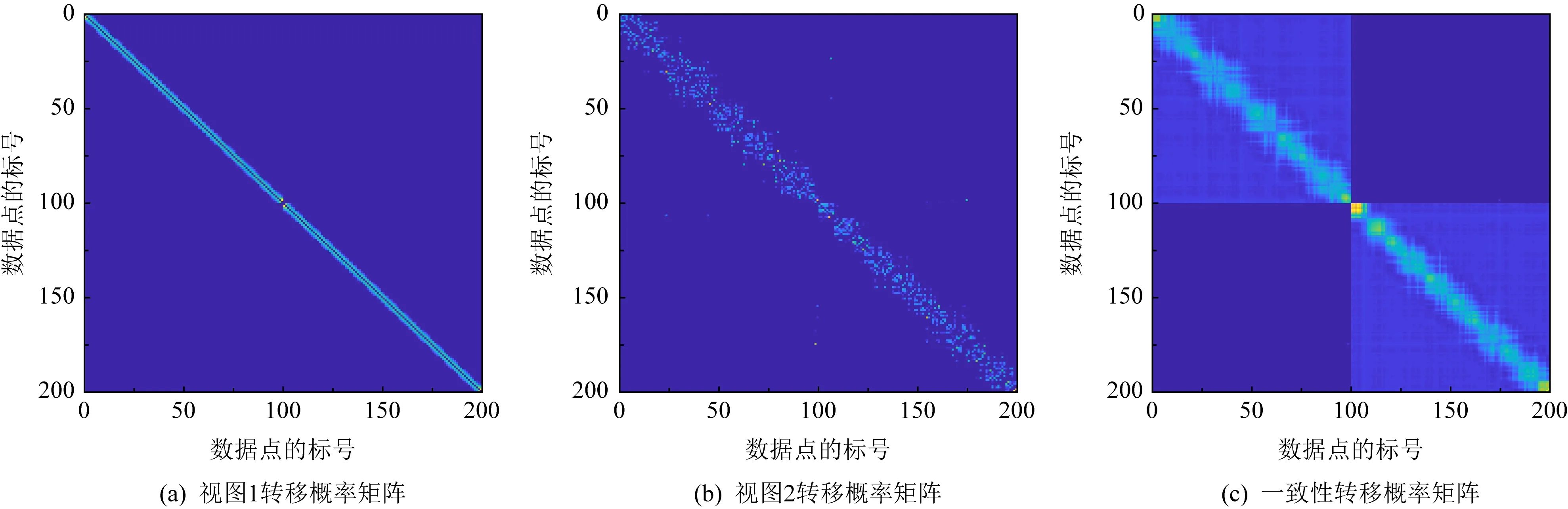
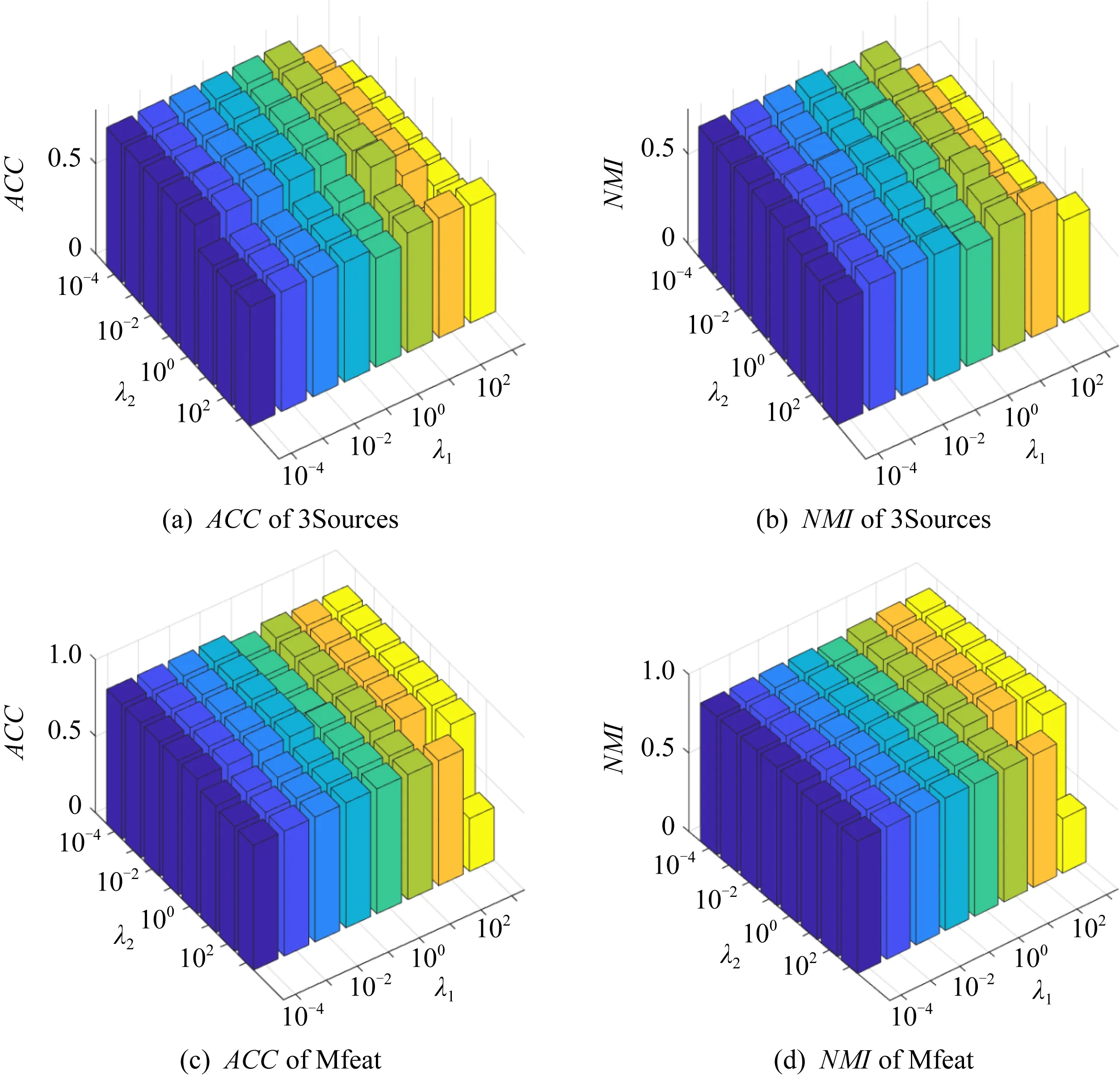
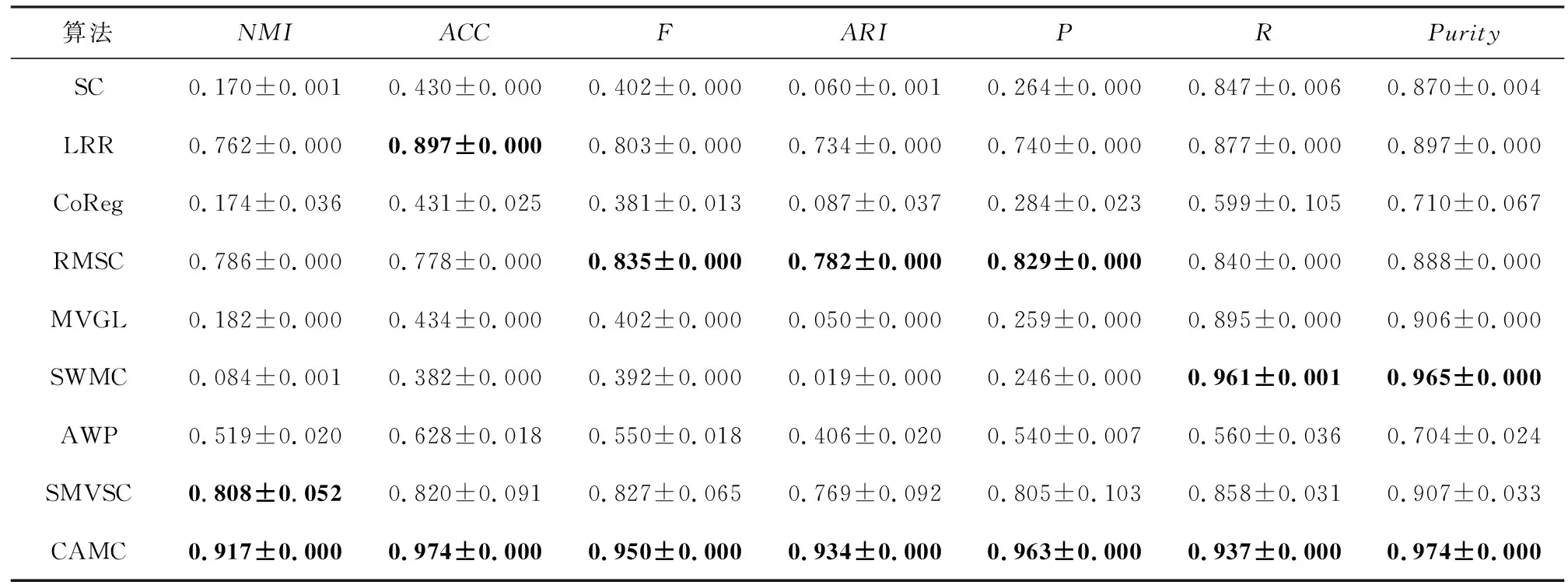
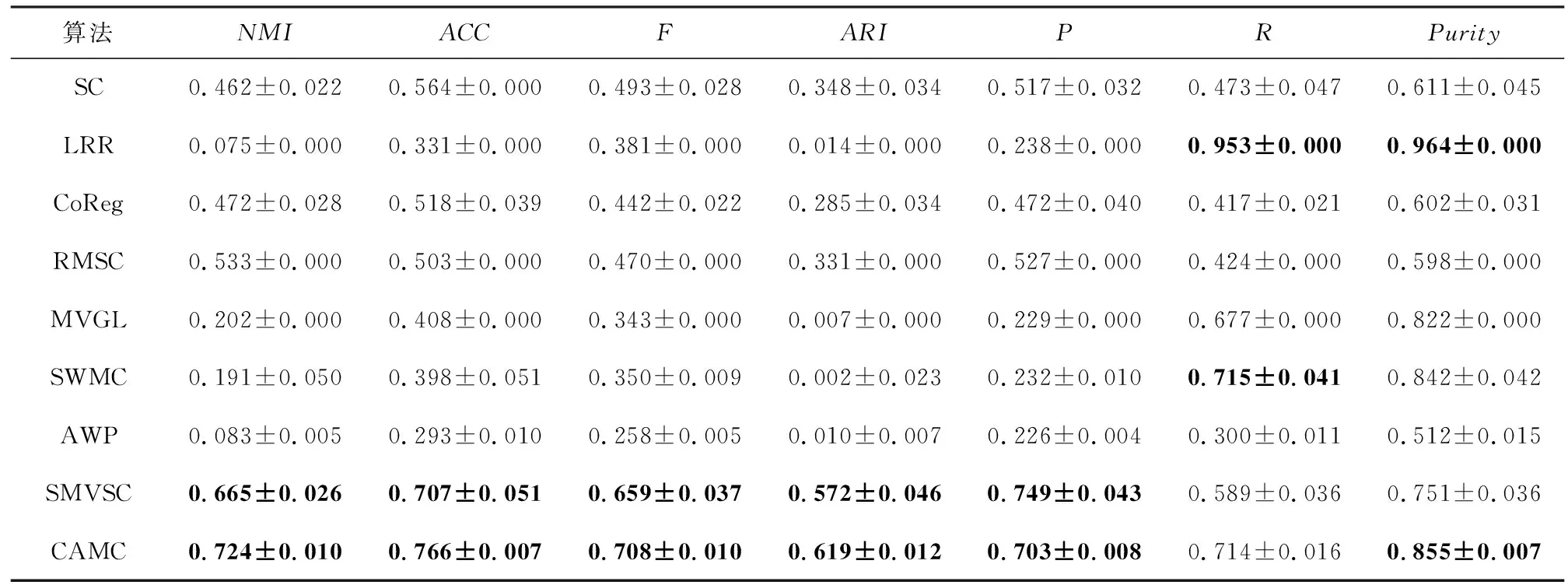
③ whileiter ④iter=iter+1; ⑤ forvfrom 1 tomdo ⑥ 根据式(5)更新w(v); ⑦ end for ⑧ 根据式(13)更新P*; ⑨ 根据式(14)更新F; ⑩ 根据式(16)更新Q; 算法CAMC的求解涉及5个子问题.求解w的复杂度为O(mn);求解P*时使用了矩阵的加法,复杂度为O(n2);求解F时涉及了特征向量分解,复杂度为O(n3);求解Q时使用了奇异值分解,复杂度为O(n3);更新乘子Y的复杂度为O(n2),所以整个算法的复杂度为O(n3+n2). 根据文献[10],式(14)是凸函数,由于F范数和核范数均是凸函数,根据文献[30],式(9)是凸的. 本文提出的优化算法在每次迭代时,需要求解式(10)(13)(14)(16)(17).根据已有文献[10,25],这几个问题都是凸的,这确保了算法1能够收敛到问题的最优解. 为了对算法进行评估,在人造数据集和真实数据集两大类数据集上进行了实验,采用了7个常用的聚类指标:标准化互信息(normalized mutual information,NMI)、准确率(accuracy,ACC)、F分数(F)、调整后的兰德指数(adjusted rand index,ARI)、精度(precision,P)、召回率(recall,R)、纯度(Purity).这些指标的定义参见文献[31],它们的值越高,聚类效果越好. 在文献[32]提供的人造数据集双月(Two-Moon)上进行了实验.如图3(a),3(b)所示,该数据集包含了2个视图,每个视图里的点都是2个月亮的形状,对应着2个簇,每个簇中有100个点,每个视图中都加上了0.12%的高斯噪声.CAMC在此数据集上聚类得到的标签和数据集中的标签是完全一致的.为了直观地对结果进行说明,进行了可视化展示.选取了距离较近但属于2个不同簇的40个点,在一致性转移概率矩阵中提取出来了相应的部分,对这40个点在2个视图中使用学到的一致性转移概率矩阵进行可视化,结果如图3(c),3(d)所示.尽管这些点距离较近,在聚类时容易出错,但CAMC能将它们分开,这表明了基于Markov链的方法是有效的.另外,该复杂图形中存在噪声,CAMC能有效将点分开证实了间接学习相似度矩阵和使用低秩正则化能够减弱噪声对聚类的影响.此外,图4展示了为各视图构造的转移概率矩阵和学习到的一致性转移概率矩阵,明显可以看出,学习到的一致性转移概率矩阵具有更好的块结构,更适合聚类.基于自动加权机制进行聚类,能够更有效地利用不同视图之间的互补信息,因而能提升聚类性能. Fig. 3 Two-Moon dataset analysis图3 Two-Moon数据集分析 Fig. 4 The transition probability matrix visualization图4 转移概率矩阵的可视化 本文选取了7个真实数据集进行实验.数据集包括:英国广播公司体育新闻数据集(BBCSport)[33]、三新闻源文本数据集(3Sources)[34]、微软逐像素标记的图像数据集v1(MSRC)[35]、Citeseer科学出版物引用网络文本数据集(Citeseer)[36]、Mfeat手写体识别数据集(Mfeat)[37]、新闻组数据集(NGs)[38]、100种植物叶子数据集(100leaves)[39].这些数据集的详细信息如表2所示. Table 2 Statistic Information of Datasets表2 数据集的相关信息 CAMC中有2个超参λ1和λ2,用来平衡目标函数中3项之间的关系.这2个超参的值域为{0.000 1,0.01,0.1,1,10,100,1 000}.在3Sources和Mfeat数据集上,使用了网格化调参法对CAMC进行参数敏感性实验,记录聚类结果的准确率值和标准化互信息值,结果如图5所示. Fig. 5 Parameter sensitivity analysis on different datasets图5 在不同数据集上的参数敏感性分析 Fig. 6 Convergence analysis on different datasets图6 在不同数据集上的算法收敛性分析 从图5中可以看出,当λ1>100时对结果较为敏感,当λ1<100时性能较为稳定;参数λ2的变化对性能影响不大,但当λ2<1时聚类效果要更好一些.总的来说,CAMC的性能是比较稳定的. Fig. 7 The t-SNE visualization on NGs dataset图7 在NGs数据集上的t-SNE可视化 为了进一步说明CAMC性能上的优势,在NGs数据集上,对每个视图的原始数据和最终学习到的一致性转移概率矩阵都通过t分布随机邻居嵌入(t-SNE)[40]进行可视化表示,如图7所示.使用各种颜色区分不同的簇.相同颜色的点越近、不同颜色的点越远表示簇的可分离性越好.从图7中可以看出,学习到的一致性转移概率矩阵的聚类效果明显优于原始数据.主要原因在于CAMC能够利用不同视图之间的互补信息,为不同视图学习最优的权重. 为了验证CAMC的有效性,本文将CAMC与8种基准算法进行了比较.其中谱聚类(SC)[41]、低秩表示子空间聚类(LRR)[42]是单视图聚类算法,基于共同正则化的聚类(CoReg)[43]、鲁棒多视图谱聚类(RMSC)[22]是经典多视图聚类算法,基于图学习的多视图聚类(MVGL,2017Transactions)[10]、基于图的自加权多视图聚类(SWMC,2017IJCAI)[44]、自适应加权法(AWP,2018KDD)[45]、稀疏多视图谱聚类(SMVSC,2020Nerocomputing)[15]是最新多视图聚类算法.对于每一种算法,都根据该算法所在的文献在所有的数据集上调参. 本文选取了7个真实数据集来验证CAMC的性能.在每个数据集上,先找出结果最好的参数,然后使用该参数的值重复进行30次实验,记录平均值和均值.结果如表3~9所示,每个数据集上每个评价指标中最好的2个结果加粗显示. Table 3 Clustering Results (Mean±Standard Deviation) on the BBCSport Dataset表3 在BBCSport数据集上的聚类结果(平均值±标准差) Table 4 Clustering Results (Mean±Standard Deviation) on the 3Sources Dataset表4 在3Sources数据集上的聚类结果(平均值±标准差) Table 5 Clustering Results (Mean±Standard Deviation) on the MSRC Dataset表5 在MSRC数据集上的聚类结果(平均值±标准差) Table 6 Clustering Results (Mean±Standard Deviation) on the Citeseer Dataset表6 在Citeseer数据集上的聚类结果(平均值±标准差) Table 7 Clustering Results (Mean±Standard Deviation) on the Mfeat Dataset表7 在Mfeat数据集上的聚类结果(平均值±标准差) Table 8 Clustering Results (Mean±Standard Deviation) on the NGs Dataset表8 在NGs数据集上的聚类结果(平均值±标准差) Table 9 Clustering Results (Mean±Standard Deviation) on the 100leaves Dataset表9 在100leaves数据集上的聚类结果(平均值±标准差) 由表3~9可知,在这9种算法中CAMC结果最好,它在BBCSport,3Sources,Citeseer,NGs,100leaves数据集上的评价指标结果基本上都是最优的.特别是在BBCSport数据集上,在NMI,ACC,F,ARI,P等评价指标上,CAMC分别以10.9%,7.7%,11.5%,15.2%,13.4%的优势拉开了与第2名之间的距离. 从结果中,本文有4方面的思考: 1) 总的来说,多视图算法的聚类性能要优于单视图算法.和单视图算法相比,多视图算法能够利用来自不同视图的多种互补信息,从而提高聚类的能力. 2) CAMC在多种类型的图像和文本数据集上均表现优异,这说明CAMC对各类型的数据集具有鲁棒性. 3) CAMC的聚类性能远优于RMSC.这2种方法都是基于Markov链的多视图谱聚类算法,RMSC将各个视图同等对待,而CAMC则考虑了不同视图之间的差异,为各个视图学习最优的权值,这表明为每个视图学习相应的权值能提高聚类的准确性. 4) 在对比算法中,SWMC和AWP均考虑了不同视图的差异性,但它们和CAMC仍然存在差距,这表明了基于Markov链聚类算法的有效性. 本文提出了一种基于Markov链的多视图谱聚类算法,利用了多个视图之间的互补信息,并考虑了各视图在聚类中发挥的不同作用,为各视图学到最优权值.此外,该算法对一致性转移概率矩阵的拉普拉斯矩阵进行了秩约束,以确保拉普拉斯图中连通分量的数目与聚类的数目完全相等.基于ADMM,提出了一种优化策略来对目标函数进行求解.在人造数据集和真实数据集上进行了大量实验,结果表明了CAMC是有效的.将来,我们会基于锚点等策略将CAMC扩展到大规模数据集上. 作者贡献声明:于晓负责研究方案设计和实验实现, 以及论文设计、撰写和修改; 刘慧设计研究方案,指导并参与论文修订; 林毓秀负责数据的整理和校对; 张彩明参与论文修订.2.3 算法复杂度和收敛性
3 实 验
3.1 人造数据集实验分析

3.2 真实数据集简介

3.3 参数敏感性分析和算法收敛性验证

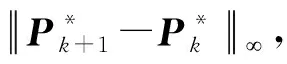

3.4 性能可视化
3.5 对比算法
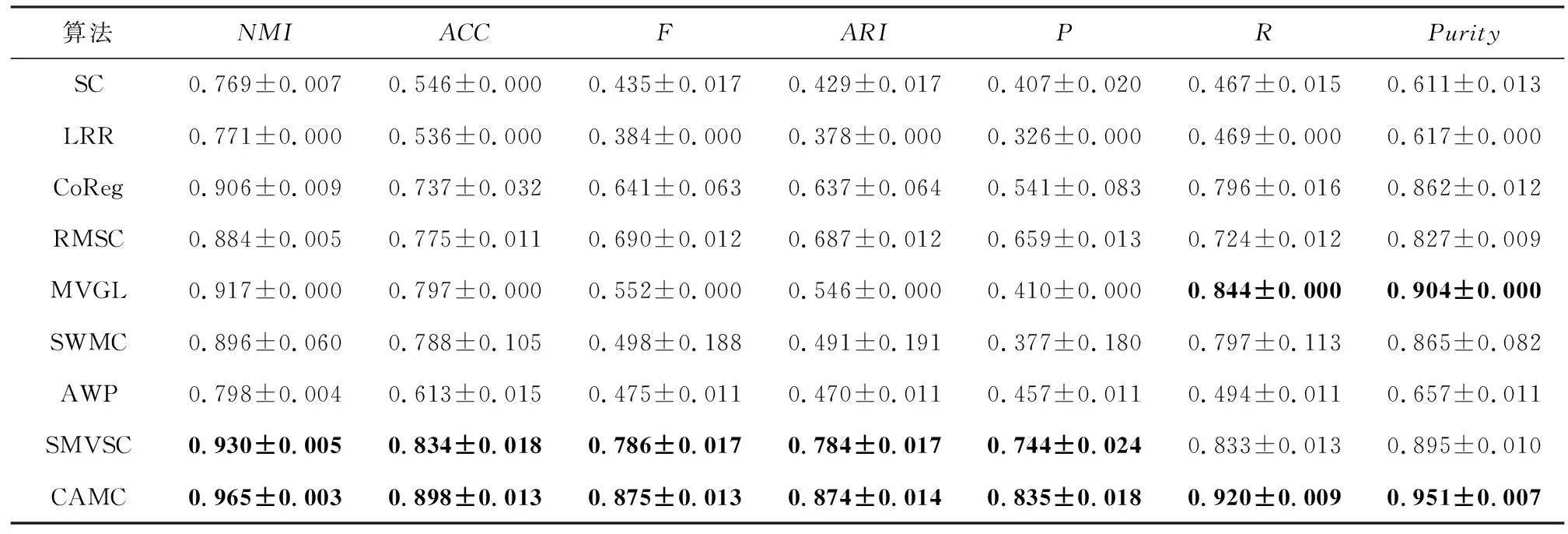
3.6 真实数据集的实验分析




4 结 论
